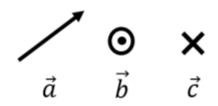25.2: Vectores

Hasta el momento, hemos visto cómo usar un sistema de coordenadas para describir la posición de un solo punto en el espacio relativo a un origen. En esta sección, introducimos la noción de un “vector”, que nos permite describir cantidades que tienen una magnitud y una dirección. Por ejemplo, puedes usar un vector para describir el hecho de que caminaste 5 km en dirección Norte. Un vector puede ser visualizado por una flecha. La longitud de la flecha es la magnitud que deseamos describir, y la dirección de la flecha corresponde a la dirección que nos gustaría describir.

A diferencia de un punto en el espacio, los vectores no tienen ubicación. Es decir, los vectores son simplemente una flecha, y puedes elegir dibujar esa flecha donde quieras. En el espacio bidimensional, se requieren dos números para definir completamente un vector. En el espacio tridimensional, se requieren tres números para definir completamente un vector. La Figura A1.2.1 muestra un vector bidimensional$\vec d$, dos veces. Debido a que ambas flechas en la figura tienen la misma magnitud y dirección, representan el mismo vector. Cuando nos referimos a cantidades que son vectores, usualmente dibujamos una flecha encima de la cantidad ($\vec d$) para indicar que son vectores. Usamos la palabra “escalar” para referirnos a números que no son vectores (un número regular también se llama escalar para distinguirlo de una cantidad que es un vector).

Figura A1.2.1: Un vector$\vec d$ mostrado dos veces, una con sus componentes cartesianos$(dx, dy)$ y otra con su magnitud y dirección$(d, φ)$.

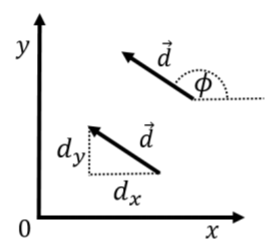
En analogía con los sistemas de coordenadas, tenemos múltiples formas de elegir los números que usamos para describir el vector. La opción más conveniente suele ser usar los “componentes cartesianos” del vector que corresponden a la longitud del vector cuando se proyecta sobre un sistema de coordenadas cartesianas. Por ejemplo, en la Figura A1.2.1, los componentes cartesianos del vector$\vec d$ se etiquetan como ($d_x$,$d_y$) indicando que el vector tiene una longitud de$d_x$ en la$x$ dirección y$d_y$ en $y$dirección. Además, el número$d_x$ es negativo, ya que el vector apunta en la$x$ dirección negativa. Otra opción común es usar la longitud del vector, que etiquetamos$d$ (el nombre del vector sin la flecha en la parte superior), y el ángulo,$\phi$ que el vector hace con el$x$ eje -eje, como se ilustra en la Figura A1.2.1. En cuanto a los componentes cartesianos bidimensionales, la magnitud del vector viene dada por: $$\begin{aligned} d&= ||\vec d||= \sqrt{d_x^2+d_y^2}\end{aligned}$$ donde también introdujimos la notación de que colocando dos barras verticales alrededor de un vector ($||\vec d||$) se utiliza para indicar su magnitud. Tenga en cuenta que en tres dimensiones, generalmente no es conveniente especificar la dirección a menos que el vector se encuentre en uno de los planos definidos por el sistema de coordenadas (por ejemplo, el$xy$ plano). En tres dimensiones, suele ser más conveniente especificar los tres componentes cartesianos.

Vectores unitarios

Una categoría especial de vectores es “vectores unitarios”, que son simplemente vectores que tienen una longitud (magnitud) de 1 (en las unidades que se defina el sistema de coordenadas). Los vectores unitarios son particularmente útiles para indicar la dirección. Por ejemplo, en la Figura A1.2.1, nos puede interesar indicar la dirección del vector$\vec d$. Los vectores unitarios se denotan usando un “sombrero” en lugar de una flecha. Así, el vector$\hat d$, es el vector de longitud 1 que apunta en la misma dirección que$\vec d$. Los componentes (cartesianos) de$\hat d$ se encuentran fácilmente dividiendo los componentes correspondientes de$\vec d$ por$d$ (la magnitud): $$\begin{aligned} (\hat d)_x &= \frac{d_x}{d}=\frac{d_x}{\sqrt{d_x^2+d_y^2}}\\ (\hat d)_y &= \frac{d_y}{d}=\frac{d_y}{\sqrt{d_x^2+d_y^2}}\\ \therefore d &= ||\hat d||=\sqrt{(\hat d)_x^2+(\hat d)_y^2}=\sqrt{\frac{d_x^2}{d_x^2+d_y^2}+\frac{d_y^2}{d_x^2+d_y^2}}=1\end{aligned}$$

Un tipo específico de vector unitario son los vectores de unidades que son paralelos a los ejes del sistema de coordenadas. Esos vectores se denotan$\hat x$,$\hat y$,$\hat z$ (y a veces$\hat i$$\hat j$,,$\hat k$ o$\hat e_x$,$\hat e_y$,$\hat e_z$) para el$x$, $y$, y$z$ ejes, respectivamente. Así, el vector$d\hat{x}$, es el vector de longitud$d$ que apunta en la$x$ dirección positiva.

Notaciones y representación de vectores

Existen múltiples notaciones para describir un vector usando sus componentes. Las siguientes son todas formas equivalentes de anotar el vector$\vec d$ en términos de sus componentes$d_x$ y$d_y$: $$\begin{aligned} \vec d &= (d_x,d_y)\quad&\text{row vector}\\ &=\begin{pmatrix} d_x \\ d_y \\ \end{pmatrix}\quad&\text{column vector}\\ &= d_x\hat x +d_y \hat y\quad&\text{using }\hat x,\;\hat y\\ &=d_x\hat i +d_y \hat j \quad&\text{using }\hat i,\;\hat j\end{aligned}$$ Los vectores$\hat x$ ($\hat i$) y$\hat y$ ($\hat j$) son unidades vectores en$x$ y$y$ direcciones respectivamente. Por ejemplo, el vector unitario$\hat y$ puede escribirse como (0,1) en dos dimensiones o (0,1,0) en tres dimensiones, usando la notación de fila.

Ejercicio$\PageIndex{1}$

Cuál es la magnitud (la longitud) del vector$5\hat x-2\hat y$?

1. $3.0$
2. $5.4$
3. $7.0$
4. $10.0$

Contestar

Ilustrar un vector gráficamente en dos dimensiones es sencillo, pero difícil en tres dimensiones. Para ayudar a remediar esto, se introduce una notación con el fin de dibujar vectores que apunten dentro o fuera de la página (perpendiculares al plano de la página). La notación proviene de imaginar que el vector es una flecha de tiro con arco. Si el vector está saliendo de la página (¡a ti!) , entonces verías la cabeza de la flecha, que representamos como un círculo con un punto (el punto es el punto de la flecha, el círculo es la base de la punta de flecha de forma cónica). Si en cambio, el vector apunta hacia la página, entonces verías la parte posterior de la flecha, que representamos como una cruz (siendo la cruz las plumas en la cola de la flecha). Esto se ilustra en la Figura A1.2.2.

Figura A1.2.2: Representación geométrica de tres vectores. El vector$\vec a$ se encuentra en el plano de la página, el vector$\vec b$ apunta hacia fuera de la página y el vector$\vec c$ apunta hacia la página.