25.3: Álgebra vectorial

En esta sección, describimos las diversas operaciones algebraicas que se pueden realizar utilizando vectores.

Multiplicación/división de un vector por un escalar

Se puede multiplicar (o dividir) un vector por un escalar (un número). Supongamos que se nos da un vector\(\vec v=(v_x, v_y, v_z)\) y un escalar\(a\). La multiplicación\(a\vec v\) se define como un nuevo vector, digamos\(\vec w\), cuyos componentes son los componentes de\(\vec v\) multiplicado por\(a\):\[\begin{aligned} \vec w = a\vec v = (av_x, a v_y, av_z)\end{aligned}\] Del mismo modo, la división de un vector por un escalar se define de manera análoga dividiendo cada Componente cartesiano por el escalar::\[\begin{aligned} \vec w = \frac{\vec v}{a} = \left(\frac{v_x}{a}, \frac{v_y}{a}, \frac{v_z}{a}\right)\end{aligned}\]

Ejercicio\(\PageIndex{1}\)

¿Qué sucede con la longitud de un vector si el vector se multiplica por\(2\) (a scalar)?

1. La longitud se dobla
2. La longitud se ha reducido a la mitad
3. La longitud es cuadruplicada
4. Depende de la dirección del vector

Contestar

En particular, esto facilita determinar el vector unitario,\(\hat v\), que apunta en la misma dirección que\(\vec v\):\[\begin{aligned} \hat v = \frac{\vec v}{v}\end{aligned}\] donde\(v\) está la magnitud (escalar) de\(\vec v\).

Sumación/resta de dos vectores

La suma de dos vectores,\(\vec a\) y\(\vec b\), se encuentra sumando los componentes de los dos vectores. De igual manera, la diferencia entre dos vectores se encuentra restando los componentes. Por ejemplo, si\(\vec c=\vec a+\vec b\), los componentes de\(\vec c\) están dados por:\[\begin{aligned} \vec c &= \vec a + \vec b = \begin{pmatrix} a_x \\ a_y \\ \end{pmatrix} + \begin{pmatrix} b_x \\ b_y \\ \end{pmatrix}\\ \therefore \begin{pmatrix} c_x \\ c_y \\ \end{pmatrix} &=\begin{pmatrix} a_x+b_x \\ a_y+b_y \\ \end{pmatrix}\end{aligned}\] donde elegimos usar la notación “vector de columna”. La notación vectorial de columna resalta el hecho de que el álgebra (suma, resta) se realiza independientemente en los\(y\) componentes\(x\) y. Por lo tanto, podemos usar escribir esta suma de manera equivalente como dos ecuaciones escalares, una para cada coordenada:\[\begin{aligned} c_x &= a_x+b_x\\ c_y &= a_y+b_y\end{aligned}\] Los vectores pueden usarse así como una notación de mano corta para representar múltiples ecuaciones (una ecuación por componente). Cuando usamos vectores para escribir una ecuación como: realmente\[\begin{aligned} \vec F = m\vec a\end{aligned}\] queremos decir que hay una ecuación escalar por componente de los vectores:\[\begin{aligned} F_x &= ma_x\\ F_y &= ma_y\\ F_z &= ma_z\end{aligned}\]

Ejemplo\(\PageIndex{1}\)

Dados dos vectores,\(\vec a=2\hat x+3\hat y\), and \(\vec b=5\hat x-2\hat y\), calculate the vector \(\vec c= 2\vec a- 3\vec b\).

Solución:

Esto se puede resolver fácilmente algebraicamente recopilando términos para cada componente,\(\hat x\) y\(\hat y\):\[\begin{aligned} \vec c &= 2\vec a- 3\vec b\\ &=2 (2\hat x+3\hat y) - 3 (5\hat x-2\hat y) \\ &=(4\hat x+6\hat y)-(15\hat x-6\hat y) \\ &=(4-15)\hat x + (6+6) \hat y\\ &= -11 \hat x + 12 \hat y\end{aligned}\] Podemos pensar que estas operaciones se realizan independientemente en los componentes:\[\begin{aligned} c_x&=2a_x-3b_x=-11\\ c_y&=2a_y-3b_y=12\end{aligned}\]

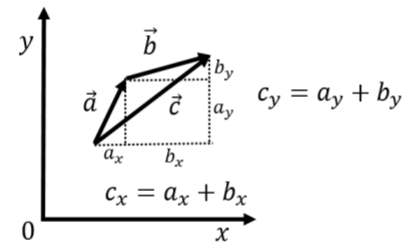
Geométricamente, se puede visualizar fácilmente la suma y resta de vectores. Esto se ilustra en la Figura A1.3.1 para el caso de agregar vectores\(\vec a\) y\(\vec b\) para obtener el vector\(\vec c\). Geométricamente, la suma de los vectores\(\vec a\) y\(\vec b\) (a veces también llamada el “resultante”) se puede encontrar por:

1. Colocar la “cola” del vector\(\vec b\) en la “cabeza” de\(\vec a\) (piense en una flecha, la parte puntiaguda es la cabeza y la parte plumosa es la cola)
2. Dibujando el vector que va de la cola del vector\(\vec a\) a la cabeza del vector\(\vec b\).

Figura A1.3.1: Adición geométrica de los vectores\(\vec a\) y\(\vec b\) colocándolos “cabeza a cola”.

La resta geométricamente de dos vectores se realiza de la misma manera que la suma. Por ejemplo, el vector\(\vec c\), dado por también se\(\vec c=\vec a -\vec b\) puede expresar como\(\vec c = \vec a + (-1) \vec b\). Es decir, primero multiplique el vector\(\vec b\) por menos 1 (que simplemente invierte su dirección), luego agregue ese vector, “cabeza a cola”, al vector\(\vec a\).

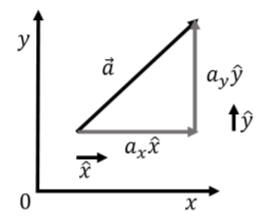
Ahora que sabemos cómo agregar vectores, podemos entender mejor la notación\(\vec a = a_x \hat x+ a_y\hat y\). Esto no es simplemente una notación, sino que de hecho es algebraicamente correcta. Significa: “multiplicar el vector\(\hat x\) por\(a_x\) (dándole así una longitud de\(a_x\)) y luego sumar\(a_y\) veces el vector\(\hat y\)”. Esto se ilustra en la Figura A1.3.2, que muestra los vectores unitarios,\(\hat x\) y\(\hat y\), que luego se multiplican por\(a_x\) y\(a_y\), respectivamente, y luego se suman juntos “cabeza a cola”.

Figura A1.3.2: Ilustración de que la notación\(\vec a = a_{x}\hat x + a_{y}\hat y\) es de hecho la adición vectorial de\(a_{x}\hat x\) y\(a_{y}\hat y\).

El producto escalar

Hay dos formas de “multiplicar” vectores: el “producto escalar” y el “producto vectorial”. El producto escalar (o “producto punto”) toma dos vectores y da como resultado un escalar (un número). El producto vectorial (o “producto cruzado”) toma dos vectores y da como resultado un tercer vector.

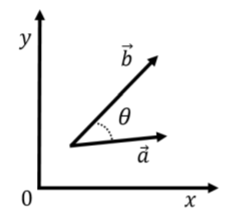
El producto escalar,\(\vec a \cdot \vec b\), de dos vectores\(\vec a\) y\(\vec b\), se define como lo siguiente: Es\[\begin{aligned} \vec a \cdot \vec b=a_xb_x +a_yb_y\end{aligned}\] decir, uno multiplica los componentes individuales de los dos vectores y luego agrega esos productos para cada componente. Esto se extiende fácilmente al caso tridimensional agregando un término\(a_zb_z\) a la suma. El producto escalar también se relaciona con el ángulo entre los dos vectores cuando los vectores se colocan “cola a cola”, como en la Figura A1.3.3\[\begin{aligned} \vec a \cdot \vec b= ab\cos\theta\end{aligned}\]

Figura A1.3.3: Ilustración del ángulo entre vectores\(\vec a\) y\(\vec b\) cuando estos se colocan cola a cola.

El producto escalar entre dos vectores de una longitud fija será máximo cuando los dos vectores sean paralelos (\(\cos\theta=1\)) y cero cuando los vectores sean perpendiculares (\(\cos\theta =0\)). El producto escalar es así útil cuando queremos calcular cantidades que son máximas cuando dos vectores son paralelos.

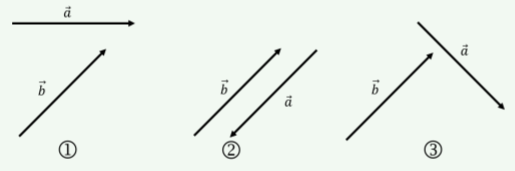
Ejercicio\(\PageIndex{2}\)

Los vectores\(\vec a\) y\(\vec b\) en los tres diagramas siguientes tienen la misma magnitud. Ordene los diagramas desde el que da el producto escalar más pequeño\(\vec a\cdot \vec b\) hasta el producto escalar más grande.

Figura A1.3.4: Ponlos en orden de la magnitud de su producto escalar.

Contestar

\(2<3<1\)

El producto vectorial

El vector (o cruce) producto toma dos vectores para producir un tercer vector que es mutuamente perpendicular a ambos vectores. El producto vectorial solo tiene significado en tres dimensiones. Dos vectores que no son colineales, es decir, no se pueden organizar de manera que se encuentren a lo largo de la misma línea, siempre se pueden utilizar para definir un plano en tres dimensiones. El producto cruzado de esos dos vectores dará un tercer vector que es perpendicular al plano (haciéndolo perpendicular a ambos vectores).

Algebraicamente, los tres componentes del producto vector,\(\vec a\times \vec b\), de vectores\(\vec a\) y\(\vec b\) se encuentran de la siguiente manera:

\[ \vec a \times \vec b =\begin{pmatrix} a_yb_z - a_z b_y\\ a_zb_x - a_x b_z\\ a_xb_y - a_y b_x\\ \end{pmatrix}\]

Una propiedad importante a tener en cuenta es que\(\vec a \times \vec b = -\vec b \times \vec a\); es decir, el producto cruzado no es conmutativo (el orden importa). La magnitud del vector obtenido por un producto cruzado viene dada por:

\[ ||\vec a \times \vec b ||=ab\sin\theta\]

donde\(\theta\) está el ángulo entre los vectores\(\vec a\) y\(\vec b\) cuando estos se colocan cola a cola (Figura A1.3.3). El vector resultante de un producto cruzado será nulo (tendrá una longitud cero) si los vectores\(\vec a\) y\(\vec b\) son paralelos, y tendrá una longitud máxima cuando estos sean perpendiculares. El producto cruzado es útil para determinar cantidades que son máximas cuando dos vectores son perpendiculares.

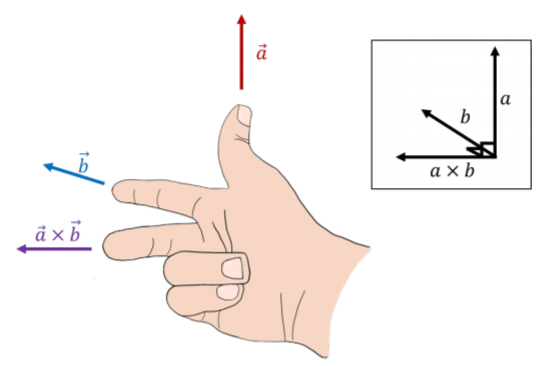
Geométricamente, se puede determinar la dirección del producto cruzado de dos vectores usando una “regla de la mano derecha”. Para distinguirla de otra regla de la mano derecha (ver Sección A1.4), la llamaremos “la regla de la mano derecha para el producto cruzado”). Esto se hace usando tu mano derecha, alineando tu pulgar con el primer vector y tu índice con el segundo vector. El producto cruzado apuntará en la dirección de tu dedo medio (cuando sostengas tu dedo medio perpendicular a los otros dos dedos). Esto se ilustra en la Figura A1.3.5. Por lo tanto, a menudo puede evitar usar la Ecuación A1.3.1 y en su lugar usar la regla de la mano derecha para determinar la dirección del producto cruzado y la Ecuación A1.3.2 para encontrar su magnitud.

Figura A1.3.5: Usando la regla de la mano derecha para productos cruzados para encontrar la dirección del producto cruzado de vectores\(\vec a\) (hacia arriba) y\(\vec b\) (hacia la página).

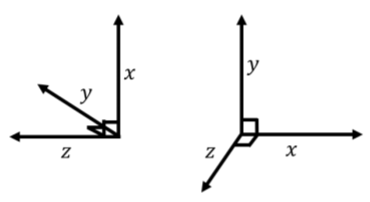
Los vectores unitarios que definen un sistema de coordenadas tienen las siguientes propiedades relativas al producto cruzado:\[\begin{aligned} \vec x \times \vec y &= \vec z\\ \vec y \times \vec z &= \vec x\\ \vec z \times \vec x &= \vec y\\\end{aligned}\] Para que estas propiedades sean correctas, cabe señalar que la dirección del\(z\) eje en tres dimensiones se especifica por la elección de\(x\) y \(y\)ejes. Es decir, se puede elegir libremente la dirección de los\(y\) ejes\(x\) y, que luego definen un plano al que el\(z\) eje será perpendicular. La dirección del\(z\) eje debe elegirse de manera que\(\vec x \times \vec y = \vec z\) (esto garantice que el sistema de coordenadas sea “diestro”), como en la Figura A1.3.6.

Figura A1.3.6: Dos orientaciones posibles para un sistema de coordenadas tridimensionales. Puedes confirmar usando la regla de la mano derecha que el\(z\) eje es el producto cruzado\(\vec x × \vec y\).