25.4: Ejemplos de usos de vectores en física

En esta sección se ofrece una rápida visión general de algunas aplicaciones de vectores en física.

Cinemática y ecuaciones vectoriales

La cinemática es la descripción de la posición y movimiento de un objeto (Capítulos 3 y 4). Las leyes de la física son los principios que en última instancia nos permiten determinar cómo cambia la posición de un objeto con el tiempo. Por ejemplo, las Leyes de Newton son un marco matemático que introduce los conceptos de fuerza y masa para modelar y determinar cómo se moverá un objeto por el espacio.

A menudo usamos un vector de posición\(\vec r(t)\),, para describir la posición de un objeto en función del tiempo. Debido a que el objeto puede moverse, el vector de posición es una función del tiempo. Un vector de posición es un vector especial en el sentido de que debe considerarse fijo en el espacio; el vector de posición para un objeto apunta desde el origen de un sistema de coordenadas hasta la ubicación del objeto.

Los tres componentes del vector de posición en coordenadas cartesianas, son las\(x\)\(z\) coordenadas\(y\),, y del objeto:\[\begin{aligned} \vec r(t) = \begin{pmatrix} x(t) \\ y(t) \\ z(t) \\ \end{pmatrix}\end{aligned}\] donde las tres coordenadas del objeto son funciones del tiempo si el objeto puede moverse. Supongamos que el objeto estaba inicialmente\(\vec r_1=(x_1, y_1, z_1)\) en posición en algún momento\(t=t_1\), y que posteriormente, en el momento\(t=t_2\), el objeto estaba en como segunda posición,\(\vec r_2=(x_1, y_1, z_1)\). Podemos definir el vector de desplazamiento,\(\vec d\), como el vector de posición\(\vec r_1\) a posición\(\vec r_2\):\[\begin{aligned} \vec d = \vec r_2 - \vec r_1 =\begin{pmatrix} x_2-x_1 \\ y_2-y_1 \\ z_2-z_1 \\ \end{pmatrix} = \begin{pmatrix} \Delta x \\ \Delta y \\ \Delta z \\ \end{pmatrix}\end{aligned}\] El vector de desplazamiento es tal que se puede agregar el vector\(\vec d\) al vector\(\vec r_1\) para describir la nueva posición del objeto en el momento\(t_2\):\[\begin{aligned} \vec d &= \vec r_2 - \vec r_1\\ \therefore \vec r_2 &= \vec r_1 + \vec d\end{aligned}\] Los componentes del vector de desplazamiento,,\(\Delta x\)\(\Delta y\), y\(\Delta z\) corresponden a los desplazamientos (la distancia recorrida) a lo largo del\(x\), \(y\), y\(z\) ejes, respectivamente. Esto se ilustra para el caso bidimensional en la Figura A1.4.1.

Figura A1.4.1: Ilustración de un vector de desplazamiento,\(\vec d = \vec r_{2} − \vec r_{1}\), para un objeto que se ubicó en posición\(\vec r_{1}\) en el tiempo\(t_{1}\) y en posición\(\vec r_{2}\) en el momento\(t_{2}\).

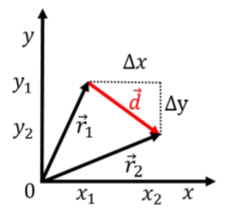
El vector de velocidad del objeto,\(\vec v=(v_x, v_y, v_z)\), se define como el vector de desplazamiento,\(\vec d\), dividido por la cantidad de tiempo (un escalar) que transcurrió,\(\Delta t=t_2-t_1\), mientras que el objeto se movió por el desplazamiento correspondiente: Se\[\begin{aligned} \vec v = \frac{\vec d}{\Delta t}=\begin{pmatrix} \frac{\Delta x}{\Delta t} \\ \frac{\Delta y}{\Delta t} \\ \frac{\Delta z}{\Delta t} \\ \end{pmatrix}\end{aligned}\] utilizó la propiedad que dividía un vector por un escalar (\(\Delta t\)) se define como dividir cada componente por el escalar. Si escribimos los componentes del vector de velocidad explícitamente, tenemos: Es\[\begin{aligned} \begin{pmatrix} v_x \\ v_y \\ v_z \\ \end{pmatrix} = \begin{pmatrix} \frac{\Delta x}{\Delta t} \\ \frac{\Delta y}{\Delta t} \\ \frac{\Delta z}{\Delta t} \end{pmatrix}\end{aligned}\] decir, podemos pensar en cada fila en esta “ecuación vectorial” como una ecuación independiente. Es decir, cuando escribimos la ecuación vectorial: en realidad solo\[\begin{aligned} \vec v = \frac{\vec d}{\Delta t}\end{aligned}\] estamos usando una notación taquigráfica para escribir las tres ecuaciones independientes que son verdaderas para cada componente individual de los vectores:\[\begin{aligned} v_x &= \frac{\Delta x}{\Delta t} \\ v_y &= \frac{\Delta y}{\Delta t} \\ v_z &= \frac{\Delta z}{\Delta t} \\\end{aligned}\] Siempre que escribimos una ecuación usando vectores, realmente estamos escribiendo múltiples ecuaciones todas a la vez, una para cada componente. Segunda Ley de Newton:\[\begin{aligned} \vec F = m \vec a\end{aligned}\] así corresponde a las tres ecuaciones (escalares):\[\begin{aligned} F_x &= ma_x\\ F_y &= ma_y\\ F_z &= ma_z\\\end{aligned}\]

Productos de trabajo y escalares

Como veremos, el “trabajo” es una cantidad escalar que nos permite determinar el cambio en la velocidad (cuadrada) de un objeto que resulta de una fuerza ejercida sobre un desplazamiento particular (Capítulo 7). Tanto la fuerza como el desplazamiento son cantidades vectoriales (una fuerza tiene una magnitud y se ejerce en una dirección particular). El trabajo,\(W\), realizado por una fuerza,\(\vec F\), sobre unos desplazamientos\(\vec d\), se define como:\[\begin{aligned} W = \vec F \cdot \vec d\end{aligned}\] El teorema de energía de trabajo nos dice que este trabajo está relacionado con el cambio en la velocidad al cuadrado del objeto a medida que se mueve a lo largo del vector de desplazamiento \(d\). Si el trabajo es cero, el objeto tiene la misma velocidad al principio y al final del desplazamiento. Si el trabajo es positivo, el objeto se mueve más rápido al final del desplazamiento (y más lento si el trabajo es negativo). Un ejemplo unidimensional se muestra en la Figura A1.4.2, que muestra una fuerza que\(\vec F\) se aplica a un bloque a medida que se desliza a lo largo del suelo sobre una distancia\(d\) (representada por el vector de desplazamiento\(\vec d\)).

Figura A1.4.2: Ejemplo de una fuerza\(\vec F\) que se aplica sobre un objeto a medida que se mueve a lo largo del vector de desplazamiento\(\vec d\).

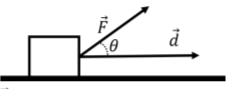
Intuitivamente, tiene sentido que solo la componente horizontal de la fuerza contribuya a cambiar la velocidad del objeto a medida que se mueve a lo largo de la trayectoria horizontal definida por el vector\(\vec d\). La componente vertical de la fuerza no contribuye a cambiar la velocidad del objeto. Así, el trabajo (el cambio de velocidad), sólo debe depender de la componente de la fuerza que sea paralela al vector de desplazamiento. El producto escalar nos permite formalizar esto en una ecuación. El producto escalar viene dado por:\[\begin{aligned} \vec F \cdot \vec d = Fd\cos\theta = F_{\parallel}d\end{aligned}\] donde introducimos\(F_{\parallel} = F\cos\theta\) como el componente de\(\vec F\) que es paralelo a\(\vec d\) (ver Figura A1.4.2). El producto escalar así “escoge” el componente de\(\vec F\) que es paralelo a\(\vec d\), que es exactamente lo que necesitamos para que el trabajo tenga sentido.

Uso de vectores para describir el movimiento rotacional

A menudo, necesitamos describir el movimiento rotacional en la física. Si un objeto está rotando, se debe especificar:

1. El eje alrededor del cual gira el objeto
2. La dirección alrededor de ese eje en el que gira el objeto (por ejemplo, en sentido horario o antihorario)
3. Qué tan rápido gira el objeto

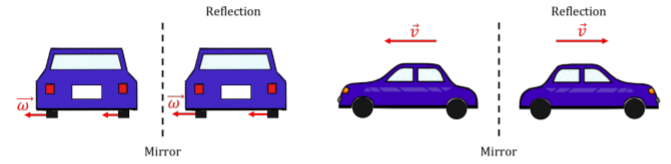
Introducimos un nuevo tipo de vector, un “vector axial”, para describir este tipo de movimiento rotacional. Elegimos la dirección del vector para que sea colineal con el eje de rotación y la magnitud del vector para representar la velocidad con la que gira el objeto. Así, nos quedan dos opciones para la dirección del vector. Por ejemplo, considere las ruedas de un automóvil que se está alejando de usted (Figura A1.4.3, el automóvil se está moviendo hacia la página). El eje de rotación es el eje de la rueda, por lo que sabemos que el vector que describe la rotación de la rueda (el vector de velocidad angular) debe apuntar ya sea a la izquierda o a la derecha.

Figura A1.4.3: Las ruedas de un automóvil que se aleja de ti.

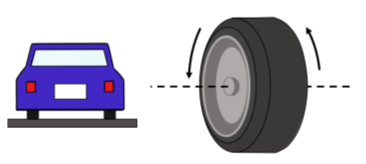
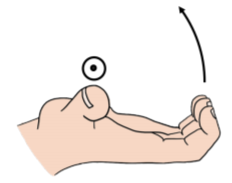
Elegimos la dirección del vector usando otra regla de la mano derecha. Nos referiremos a esto como “la regla de la mano derecha para vectores axiales” para distinguirla de la regla de la mano derecha para el producto cruzado. Al usar la regla de la mano derecha para vectores axiales, el vector apunta en la dirección de tu pulgar cuando rizas tus dedos en la dirección de rotación, como en la Figura A1.4.4. Para que el auto se aleje de ti, las ruedas estarán girando de tal manera que el punto más cercano a ti se mueva hacia arriba y el punto más alejado se mueva hacia abajo. Usando la regla de la mano derecha, encontramos que el vector de rotación apunta hacia la izquierda.

Figura A1.4.4: Uso de la regla de la derecha para cantidades axiales. En este caso, la dirección de rotación es en sentido contrario a las agujas del reloj al mirar la página (la dirección en la que se rizan los dedos), por lo que el vector de rotación apunta fuera de la página (la dirección del pulgar).

Tenemos que distinguir los vectores axiales de los vectores “verdaderos” porque no se comportan como vectores verdaderos en todos los casos. Por ejemplo, imagina que hay un espejo gigante que corre paralelo a la carretera (Figura A1.4.5). Cuando el auto se refleja en el espejo, el auto reflejado también se alejará de ti. Esto significa que las ruedas girarán en la misma dirección que antes, por lo que el vector de rotación aún apunta hacia la izquierda. Consideremos ahora un verdadero vector, como un vector de velocidad. Si el vector de velocidad apuntaba inicialmente a la izquierda (es decir, si el carro se movía hacia la izquierda), el carro reflejado se movería hacia la derecha. Entonces, esperamos que un verdadero vector cambie de dirección cuando se refleje de esta manera. Dado que el vector de rotación no siempre se comporta como un vector verdadero, lo llamamos un vector axial o un “pseudovector”.

Figura A1.4.5: Izquierda: El vector de velocidad angular para la rotación de las ruedas\(\vec ω\), que apunta a la izquierda, también apunta a la izquierda en la reflexión. Derecha: El vector de velocidad, apuntando a la izquierda, apunta a la derecha en el reflejo del automóvil. El vector de velocidad angular se denomina vector “axial” o “pseudo” porque no cambia de dirección bajo una reflexión.

Torque y productos vectoriales

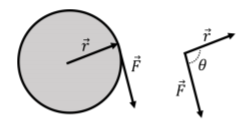
Introduciremos el concepto de par para describir cómo una fuerza puede hacer que un objeto gire. Consideremos el disco ilustrado en la Figura A1.4.6 que es libre de rotar alrededor de un eje que pasa por su centro y que es perpendicular al plano de la página. \(\vec F\)Se aplica una fuerza en el borde del disco (imagínese tirando de una cuerda unida al borde del disco), en una posición que es desplazada del eje de rotación por el vector\(\vec r\). El par,\(\vec \tau\), de la fuerza alrededor del centro del disco se define como:\[\begin{aligned} \vec\tau=\vec r\times \vec F\end{aligned}\] y representa cuánto\(\vec F\) contribuirá la fuerza a hacer que el disco gire alrededor de su eje. Si el vector de fuerza fuera paralelo al vector\(\vec r\), el disco no giraría; si tira hacia afuera en un disco, no girará alrededor de su centro. Sin embargo, si la fuerza es perpendicular al vector\(\vec r\) (es decir, tangente a la circunferencia del disco), entonces hará que el disco gire al máximo. La magnitud del par (producto cruzado) viene dada por:\[\begin{aligned} \tau =rF\sin\theta=F_{\perp}r=Fr_\perp\end{aligned}\] donde\(\theta\) está el ángulo entre los vectores cuando se colocan cola a cola, como en el lado derecho de la Figura A1.4.6. En las dos últimas igualaciones, hemos definido\(F_\perp=F\sin\theta\) o\(r_\perp=r\sin\theta\) para referirnos a la parte del vector\(\vec F\) que es perpendicular al vector\(\vec r\) o la parte del vector\(\vec r\) que es perpendicular al vector \(\vec F\). Es decir, el producto vectorial “escoge” la parte de un vector que es perpendicular al otro, que es exactamente la propiedad que necesitamos para la cantidad física de torque.

Figura A1.4.6: Una fuerza,\(\vec F\), se ejerce en el plano de un disco en una posición dada por el vector\(\vec r\) con relación al centro del disco.

Ejercicio\(\PageIndex{1}\)

Haciendo referencia a la Figura A1.4.6, ¿en qué dirección apunta el vector de par?

1. a la derecha
2. a la izquierda
3. fuera de la página
4. en la página

Contestar