11.4: Ejemplos trabajados

Ejemplo 11.1 Velocidades Relativas de Dos Planos Móviles

Un avión A viaja hacia el noreste con una velocidad de\(v_{\mathrm{A}}=160 \mathrm{m} \cdot \mathrm{s}^{-1}\). Un segundo avión B viaja al sureste con una velocidad de\(v_{\mathrm{B}}=200 \mathrm{m} \cdot \mathrm{s}^{-1}\). (a) Elija un sistema de coordenadas y escriba una expresión para la velocidad de cada avión como vectores,\(\overrightarrow{\mathbf{V}}_{\mathrm{A}}\) y use\(\overrightarrow{\mathbf{V}}_{B}\) cuidadosamente vectores unitarios para expresar su respuesta. (b) Esbozar los vectores\(\overrightarrow{\mathbf{V}}_{\mathbf{A}}\) y\(\overrightarrow{\mathbf{V}}_{\mathbf{B}}\) en su sistema de coordenadas. (c) Encontrar una expresión vectorial que exprese la velocidad de la aeronave A vista de un observador que vuela en la aeronave B. Calcular este vector. ¿Cuál es su magnitud y dirección? Esbosquelo en su sistema de coordenadas.

Figura 11.2 (b): Sistema de coordenadas

Un observador en reposo con respecto al suelo define un marco de referencia\(S\). Elija un sistema de coordenadas que se muestra en la Figura 11.2b. Según este observador, el avión A se mueve con velocidad\(\overrightarrow{\mathbf{v}}_{\mathrm{A}}=v_{\mathrm{A}} \cos \theta_{\mathrm{A}} \hat{\mathbf{i}}+v_{\mathrm{A}} \sin \theta_{\mathrm{A}} \hat{\mathbf{j}}\), y el avión B se mueve con velocidad\(\overrightarrow{\mathbf{v}}_{\mathrm{B}}=v_{\mathrm{B}} \cos \theta_{\mathrm{B}} \hat{\mathbf{i}}+v_{\mathrm{B}} \sin \theta_{\mathrm{B}} \hat{\mathbf{j}}\). De acuerdo con la información dada en el problema el avión A vuela hacia el noreste así\(\theta_{\mathrm{A}}=\pi / 4\) y el avión B vuela al sureste así\(\theta_{\mathrm{B}}=-\pi / 4\). Así\(\overrightarrow{\mathbf{v}}_{\mathrm{A}}=\left(80 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right) \hat{\mathbf{i}}+\left(80 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right) \hat{\mathbf{j}}\) y\(\overrightarrow{\mathbf{v}}_{\mathrm{B}}=\left(100 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right) \hat{\mathbf{i}}-\left(100 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right) \hat{\mathbf{j}}\).

Considera que un segundo observador se mueve junto con el avión B, definiendo el marco de referencia S′. ¿Cuál es la velocidad del avión A según este observador que se mueve en el avión B? La velocidad del observador que se mueve en el avión B con respecto a un observador en reposo en el suelo es solo la velocidad del avión B y viene dada por\(\overrightarrow{\mathbf{V}}=\overrightarrow{\mathbf{v}}_{\mathrm{B}}=v_{\mathrm{B}} \cos \theta_{\mathrm{B}} \hat{\mathbf{i}}+v_{\mathrm{B}} \sin \theta_{\mathrm{B}} \hat{\mathbf{j}}\). Usando la Ley de Adición de Velocidades, Ecuación (11.3.2), la velocidad del avión A con respecto a un observador que se mueve junto con el Avión B viene dada por

\ [\ begin {alineado}
\ overrightarrow {\ mathbf {v}} _ {\ mathrm {A}} ^ {\ prime} &=\ overrightarrow {\ mathbf {v}} _ {\ mathrm {A}} -\ overrightarrow {\ mathbf {V}} =\ left (v_ {\ mathrm {A}}\ cos\ theta_ {\ mathrm {A}}\ sombrero {\ mathbf {i}} +v_ {\ mathrm {A}}\ sin\ theta_ {\ mathrm {A}}\ sombrero {\ mathbf {j}}\ derecha) -\ izquierda (v_ {\ mathrm {B}}\ cos\ theta_ {\ mathrm {B}}\ sombrero {\ mathbf {i}} +v_ {\ mathrm {B}}\ sin\ theta_ {\ mathrm {B}}\ sombrero {\ mathbf {j}}\ derecha)\\
&=\ izquierda (v_ {\ mathrm {A}}\ cos\ theta_ {\ mathrm {A} -v_ {\ mathrm {B}}\ cos\ theta_ {\ mathrm {B}}\ derecha)\ hat {\ mathbf {i}} +\ left (v_ {\ mathrm {A}}\ sin\ theta_ {\ mathrm {A}} -v_ {\ mathrm {B}}\ sin\ theta_ {\ mathrm {B}}\ derecha)\ hat {\ mathbf {j}}\\
&=\ izquierda (\ izquierda (80\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ derecha) -\ izquierda (100\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ derecha)\ derecha)\ hat {\ mathbf {i}} +\ izquierda (\ izquierda (80\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ derecha) +\ izquierda (100\ sqrt {2}\ mathrm {m}\ cdot\ mathrm { s} ^ {-1}\ derecha)\ derecha)\ sombrero {\ mathbf {j}}. \\
&=-\ izquierda (20\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ derecha)\ hat {\ mathbf {i}} +\ izquierda (180\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ derecha)\ sombrero {\ mathbf {j}\
&=v_ {A x} ^ {\ prime}\ sombrero {\ mathbf {i}} +v_ {A\ mathrm {y}} ^ {\ prime}\ sombrero {\ mathbf {j}}
\ fin {alineado}\ nonumber\]

La Figura 11.3 muestra la velocidad del avión A con respecto al avión B en el marco de referencia S'.

Figura 11.3 Avión A visto desde un observador en el avión B

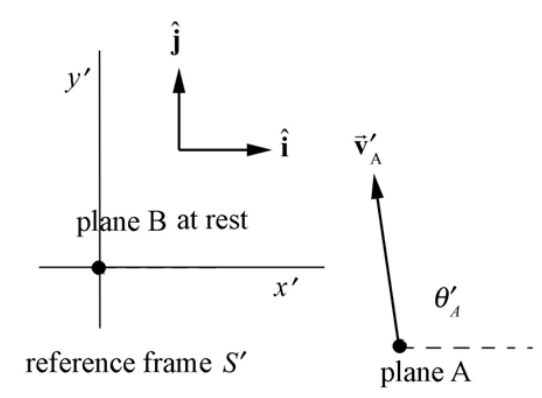
La magnitud de la velocidad del avión A vista por un observador que se mueve con el avión B viene dada por

\[\left|\vec{v}_{\mathrm{A}}^{\prime}\right|=\left(v_{A x}^{\prime 2}+v_{A y}^{\prime 2}\right)^{1 / 2}=\left(\left(-20 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right)^{2}+\left(180 \sqrt{2} \mathrm{m} \cdot \mathrm{s}^{-1}\right)^{2}\right)^{1 / 2}=256 \mathrm{m} \cdot \mathrm{s}^{-1} \nonumber \]

El ángulo de velocidad del avión A visto por un observador que se mueve con el avión B viene dado por,

\ [\ begin {alineado}
\ theta_ {A} ^ {\ prime} &=\ tan ^ {-1}\ izquierda (v_ {A y} ^ {\ prime}/v_ {A x} ^ {\ prime}\ derecha) =\ tan ^ {-1}\ izquierda (\ izquierda (\ izquierda (180\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ ^ -1}\ derecha)/\ izquierda (-20\ sqrt {2}\ mathrm {m}\ cdot\ mathrm {s} ^ {-1}\ derecha)\ derecha)\\
&=\ tan ^ {-1} (-9) =180^ {\ circ} -83. 7^ {\ circ} =96.3^ {\ circ}
\ final {alineado}\ nonumber\]

Ejemplo 11.2 Movimiento relativo y coordenadas polares

Por velocidad relativa nos referimos a la velocidad con respecto a un sistema de coordenadas especificado. (Se entiende que el término velocidad, por sí solo, es relativo al sistema de coordenadas del observador). (a) Se observa que un punto tiene velocidad\(\overrightarrow{\mathbf{V}}_{A}\), relativa al sistema de coordenadas A. ¿Cuál es su velocidad en relación con el sistema de coordenadas B, que se desplaza del sistema A por distancia\(\overrightarrow{\mathbf{R}}\)? \((\overrightarrow{\mathbf{R}}\)puede cambiar en el tiempo.) (b) Las partículas a y b se mueven en direcciones opuestas alrededor de un círculo con la magnitud de la velocidad angular ω, como se muestra en la Figura 11.4. A t = 0 ambos están en el punto\(\overrightarrow{\mathbf{r}}=\hat{l} \hat{\mathbf{j}}\) donde l es el radio del círculo. Encuentra la velocidad de a relativa a b.

Figura 11.5 Partículas a y b que se mueven una respecto a la otra

Solución: a) Los vectores de posición están relacionados por

\[\overrightarrow{\mathbf{r}}_{B}=\overrightarrow{\mathbf{r}}_{A}-\overrightarrow{\mathbf{R}} \nonumber \]

Las velocidades están relacionadas por las derivadas de toma, (ley de adición de velocidades Ecuación (11.3.2))

\[\overrightarrow{\mathbf{v}}_{B}=\overrightarrow{\mathbf{v}}_{A}-\overrightarrow{\mathbf{V}} \nonumber \]

(b) Escojamos dos marcos de referencia; el marco B está centrado en la partícula b y el marco A está centrado en el centro del círculo en la Figura 11.5. Entonces el vector de posición relativa entre los orígenes de los dos fotogramas viene dado por

\[\overrightarrow{\mathbf{R}}=l \hat{\mathbf{r}} \nonumber \]

El vector de posición de la partícula a en relación con el marco A viene dado por

\[\overrightarrow{\mathbf{r}}_{A}=l \hat{\mathbf{r}}^{\prime} \nonumber \]

El vector de posición de la partícula b en el marco B se puede encontrar sustituyendo las Ecuaciones (11.4.7) y (11.4.6) en la Ecuación (11.4.4),

\[\overrightarrow{\mathbf{r}}_{B}=\overrightarrow{\mathbf{r}}_{A}-\overrightarrow{\mathbf{R}}=l \hat{\mathbf{r}}^{\prime}-l \hat{\mathbf{r}} \nonumber \]

Podemos descomponer cada uno de los vectores unitarios\(\hat{\mathbf{r}}\) y\(\hat{\mathbf{r}}^{\prime}\) con respecto a los vectores unitarios cartesianos\(\hat{\mathbf{1}}\) y\(\hat{\mathbf{j}}\) (ver Figura 11.5),

\[\hat{\mathbf{r}}=-\sin \theta \hat{\mathbf{i}}+\cos \theta \hat{\mathbf{j}} \nonumber \]

\[\hat{\mathbf{r}}^{\prime}=\sin \theta \hat{\mathbf{i}}+\cos \theta \hat{\mathbf{j}} \nonumber \]

Entonces la Ecuación (11.4.8) que da el vector de posición de la partícula b en el marco B se convierte

\[\overrightarrow{\mathbf{r}}_{B}=l \hat{\mathbf{r}}^{\prime}-l \hat{\mathbf{r}}=l(\sin \theta \hat{\mathbf{i}}+\cos \theta \hat{\mathbf{j}})-l(-\sin \theta \hat{\mathbf{i}}+\cos \theta \hat{\mathbf{j}})=2 l \sin \theta \hat{\mathbf{i}} \nonumber \]

Para encontrar el vector de velocidad de la partícula a en el marco B (es decir, con respecto a la partícula b), diferenciar la Ecuación (11.4.11)

\[\overrightarrow{\mathbf{v}}_{B}=\frac{d}{d t}(2 l \sin \theta) \hat{\mathbf{i}}=(2 l \cos \theta) \frac{d \theta}{d t} \hat{\mathbf{i}}=2 \omega l \cos \theta \hat{\mathbf{i}} \nonumber \]

Ejemplo 11.3 Recoil en diferentes marcos

Una persona de masa\(m_{1}\) está de pie en un carro de masa\(m_{2}\). Supongamos que el carro es libre de moverse sobre sus ruedas sin fricción. La persona lanza una bola de masa\(m_{3}\) θ con respecto a la horizontal medida por la persona en el carro. El balón se lanza con una velocidad\(v_{0}\) con respecto al carro (Figura 11.6). (a) ¿Cuál es la velocidad final de la pelota vista por un observador fijado al suelo? b) ¿Cuál es la velocidad final del carro vista por un observador fijado al suelo? (c) Con respecto a la horizontal, ¿qué ángulo ve el observador fijo al balón salir del carro?

Figura 11.6 Retraso de una persona en carro debido a balón arrojado

Solución: a), b) Nuestro marco de referencia será el fijado al suelo. Tomaremos como nuestro estado inicial que antes de que se lance la pelota (carro, pelota, lanzando persona estacionaria) y nuestro estado final que después de que se lance la pelota. Estamos asumiendo que no hay fricción, por lo que no hay fuerzas externas que actúen en la dirección horizontal. El componente x inicial del impulso total es cero,

\(p_{x, 0}=0\)total

Después de lanzar la pelota, el carro y la persona tienen un impulso final

\[\overrightarrow{\mathbf{p}}_{f, \text { cart }}=-\left(m_{2}+m_{1}\right) v_{f, \text { cart }} \hat{\mathbf{i}} \nonumber \]

medida por la persona en el suelo, donde\(v_{f, cart}=0\) está la velocidad de la persona y el carro. (El centro de masa de la persona se moverá con respecto al carro mientras se lanza la pelota, pero como nos interesan las velocidades, no las posiciones, solo necesitamos asumir que la persona está en reposo con respecto al carro después de que se lance la pelota).

El balón se lanza con una velocidad\(v_{0}\) y en un ángulo θ con respecto a la horizontal medida por la persona en el carro. Por lo tanto la persona en el carro lanza la pelota con velocidad

\[\overrightarrow{\mathbf{v}}_{f, \text { ball }}^{\prime}=v_{0} \cos \theta \hat{\mathbf{i}}+v_{0} \sin \theta \hat{\mathbf{j}} \nonumber \]

Debido a que el carro se mueve en la dirección x negativa con velocidad\(v_{f, cart}=0\) justo cuando la pelota sale de la mano de la persona, el componente x de la velocidad de la pelota medida por un observador en el suelo viene dado por

\[v_{x f, \text { ball }}=v_{0} \cos \theta-v_{f, \text { cart }} \nonumber \]

La bola parece tener un componente x menor de la velocidad de acuerdo con el observador en el suelo. La velocidad de la pelota medida por un observador en el suelo es

\[\overrightarrow{\mathbf{v}}_{f, \text { ball }}=\left(v_{0} \cos \theta-v_{f, \text { cart }}\right) \hat{\mathbf{i}}+v_{0} \sin \theta \hat{\mathbf{j}} \nonumber \]

El impulso final de la pelota según un observador en el suelo es

\[\overrightarrow{\mathbf{p}}_{f, \text { ball }}=m_{3}\left[\left(v_{0} \cos \theta-v_{f, \text { can }}\right) \hat{\mathbf{i}}+v_{0} \sin \theta \hat{\mathbf{j}}\right] \nonumber \]

El diagrama de flujo de momento se muestra en (Figura 11.7).

Figura 11.7 Diagrama de flujo de impulso para retroceso

Debido a que el componente x del impulso del sistema es constante, tenemos que

\ [\ begin {aligned}
0 &=\ left (p_ {x, f}\ right) _ {\ text {cart}} +\ left (p_ {x, f}\ right) _ {\ text {ball}}\\
&=-\ left (m_ {2} +m_ {1}\ right) v_ {f,\ text {carrito}} +m_ {3} izquierda\ (v_ {0}\ cos\ theta-v_ {f,\ text {carrito}}\ derecha)
\ end {alineado}\ nonumber\]

Podemos resolver la Ecuación (11.4.19) para la velocidad final y velocidad del carro medida por un observador en el suelo,

\[v_{f, \text { cart }}=\frac{m_{3} v_{0} \cos \theta}{m_{2}+m_{1}+m_{3}} \nonumber \]

\[\overrightarrow{\mathbf{v}}_{f, \text { cart }}=v_{f, \text { cart }} \hat{\mathbf{i}}=\frac{m_{3} v_{0} \cos \theta}{m_{2}+m_{1}+m_{3}} \hat{\mathbf{i}} \nonumber \]

Tenga en cuenta que el componente y del momento no es constante porque a medida que la persona está lanzando la pelota está empujando fuera del carro y la fuerza normal con el suelo excede la fuerza gravitacional por lo que la fuerza externa neta en la dirección y es distinta de cero.

Sustituyendo la Ecuación (11.4.20) en la Ecuación (11.4.17) da

\ [\ begin {alineado}
\ overrightarrow {\ mathbf {v}} _ {f,\ text {bola}} &=\ left (v_ {0}\ cos\ theta-v_ {f,\ text {carrito}}\ derecha)\ hat {\ mathbf {i}} +v_ {0}\ sin\ theta\ sombrero {\ mathbf {j}}\\
=\ frac {m_ {1} +m_ {2}} {m_ {1} +m_ {2} +m_ {3}}\ izquierda (v_ {0}\ cos\ theta\ derecha)\ sombrero {\ mathbf {i}} +\ izquierda (v_ {0}\ sin\ theta\ derecha)\ hat {\ mathbf {j}}
\ end {alineado}\ nonumber\]

Como cheque, tenga en cuenta que en el límite\(m_{3}<<m_{1}+m_{2}\),\(\overrightarrow{\mathbf{V}} f, \text { ball }\) tiene velocidad\(v_{0}\) y se dirige en un ángulo θ por encima de la horizontal; el hecho de que la combinación persona-carro mucho más masiva sea libre de moverse no afecta el vuelo de la pelota como lo ve el observador fijo. También tenga en cuenta que en el límite poco realista\(m>>m_{1}+m_{2}\) la pelota se mueve a una velocidad mucho menor\(v_{0}\) que cuando sale del carro.

c) El ángulo\(\phi\) en el que se lanza la pelota visto por el observador en el suelo viene dado por

\ [\ begin {alineado}
\ phi &=\ tan ^ {-1}\ frac {\ izquierda (v_ {f,\ texto {bola}}\ derecha) _ {y}} {\ izquierda (v_ {f,\ texto {bola}}\ derecha) _ {x}} =\ tan ^ {-1}\ frac {v_ {0}\ sin\ theta} {\ izquierda\ (m_ {1} +m_ {2}\ derecha)/\ izquierda (m_ {1} +m_ {2} +m_ {3}\ derecha)\ derecha] v_ {0}\ cos\ theta}\\
&=\ tan ^ {-1}\ izquierda [\ izquierda (\ frac {m_ {1} +m_ {2} +m_ {3}} {m_ {1} +m_ {2}}\ derecha)\ tan\ theta\ derecha]
\ end {alineado}\ nonumber\]

Para valores arbitrarios para las masas, la expresión anterior no se reducirá a una forma simplificada. No obstante, podemos ver eso\(\tan \phi>\tan \theta\) para las masas arbitrarias, y eso en el límite\(m_{3}<<m_{1}+m_{2}, \phi \rightarrow \theta\) y en el límite poco realista\(m_{3} \gg m_{1}+m_{2}, \phi \rightarrow \pi / 2\). ¿Puedes explicar esta última predicción extraña?