15.5: Ejemplos trabajados

Ejemplo 15.1 Colisión Elástica Unidimensional entre Dos Objetos

Figura 15.7 Colisión elástica entre dos carros no idénticos

Considera la colisión elástica de dos carros a lo largo de una pista; el carro incidente 1 tiene masa\(m_{1}\ and moves with initial speed \(v_{1,i}\). El carro objetivo tiene masa\(m_{2}=2 m_{1}\) e inicialmente está en reposo,\(v_{2, i}=0\), (Figura 15.7). Inmediatamente después de la colisión, el carro incidente tiene velocidad final\(v_{1, f}\) y el carro objetivo tiene velocidad final\(v_{2, f}\). Calcular el componente x final de las velocidades de los carros en función de la velocidad inicial\(v_{1, i}\).

Solución: El diagrama de flujo de momento para los objetos antes (estado inicial) y después (estado final) de la colisión se muestra en la Figura 15.7. Podemos usar inmediatamente nuestros resultados anteriores con\(m_{2}=2 m_{1}\) y\(v_{2, i}=0\). El componente x final de la velocidad del carro 1 viene dado por la Ecuación (15.3.14), donde usamos\(v_{1 x, i}=v_{1, i}\).

\[v_{1 x, f}=-\frac{1}{3} v_{1, i} \nonumber \]El componente x final de la velocidad del carro 2 viene dado por la Ecuación (15.4.17)\[v_{2 x, f}=\frac{2}{3} v_{1, i} \nonumber \]

Ejemplo 15.2 La disipación de energía cinética en una colisión completamente inelástica entre dos objetos

Figura 15.7b Colisión inelástica entre dos carros no idénticos

Un carro incidente de masa\(m_{1}\) y velocidad inicial\(v_{1,i}\) choca completamente inelásticamente con un carro de masa\(m_{2}\) que inicialmente está en reposo (Figura 15.7b). No hay fuerzas externas que actúen sobre los objetos en la dirección de la colisión. Encuentra\(\Delta K / K_{\text {initial }}=\left(K_{\text {final }}-K_{\text {initial }}\right) / K_{\text {initial }}\)

Solución: En ausencia de cualquier fuerza neta sobre el sistema consistente en los dos carros, el impulso después de la colisión será el mismo que antes de la colisión. Después de la colisión, los carros se moverán en la dirección de la velocidad inicial del carro incidente con una velocidad común\(v_{f}\) encontrada al aplicar la condición de impulso

\[m_{1} v_{1, i}=\left(m_{1}+m_{2}\right) v_{f} \Rightarrow v_{f}=\frac{m_{1}}{m_{1}+m_{2}} v_{1, i} \nonumber \]La velocidad relativa inicial es\(v_{i}^{\mathrm{rel}}=v_{1, i}\). La velocidad relativa final es cero porque los carros se pegan juntos por lo que usando la Ecuación (15.3.26), el cambio en la energía cinética es\[\Delta K=-\frac{1}{2} \mu\left(v_{i}^{r e l}\right)^{2}=-\frac{1}{2} \frac{m_{1} m_{2}}{m_{1}+m_{2}} v_{1, i}^{2} \nonumber \] La relación del cambio en la energía cinética a la energía cinética inicial es entonces\[\Delta K / K_{\text {initial}}=-\frac{m_{2}}{m_{1}+m_{2}} \nonumber \] Como verificación, podemos calcular el cambio en la energía cinética a través de\[\Delta K=\left(K_{f}-K_{i}\right)=\frac{1}{2}\left(m_{1}+m_{2}\right) v_{f}^{2}-\frac{1}{2} v_{1, i}^{2} =\frac{1}{2}\left(m_{1}+m_{2}\right)\left(\frac{m_{1}}{m_{1}+m_{2}}\right)^{2} v_{1, i}^{2}-\frac{1}{2} v_{1, i}^{2} =\left(\frac{m_{1}}{m_{1}+m_{2}}-1\right)\left(\frac{1}{2} m_{1} v_{1, i}^{2}\right)=-\frac{1}{2} \frac{m_{1} m_{2}}{m_{1}+m_{2}} v_{1, i}^{2} \nonumber \]

de acuerdo con la Ecuación (15.4.4).

Ejemplo 15.3 Superbolas que rebotan

Figura 15.8b Dos superbolas cayendo

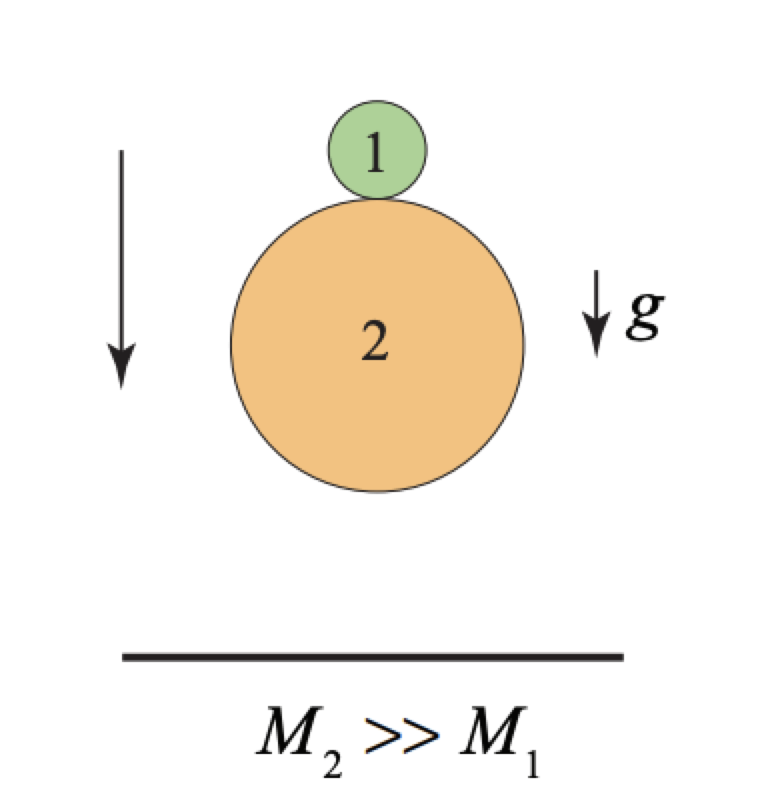
Considera dos bolas que se dejan caer desde una altura sobre el suelo, una\(h_{i}\) encima de la otra (Figura 15.8). La bola 1 está en la parte superior y tiene masa\(M_{1}\), y la bola 2 está debajo y tiene masa\(M_{2}\) con\(M_{2}>>M_{1}\). Supongamos que no hay pérdida de energía cinética durante todas las colisiones. La bola 2 primero choca con el suelo y rebota. Entonces, a medida que la bola 2 comienza a moverse hacia arriba, choca con la bola 1 que sigue moviéndose hacia abajo (figura abajo a la izquierda). ¿Qué tan alto rebotará la bola 1 en el aire? Pista: considera esta colisión como la ve un observador que se mueve hacia arriba con la misma velocidad que tiene la bola 2 después de que choca con el suelo. ¿Qué velocidad tiene la bola 1 en este marco de referencia después de que choca con la bola 2?

Solución

El sistema consta de dos bolas y la tierra. Hay cinco estados especiales para esta moción que se muestran en la siguiente figura.

parte a)

Estado Inicial: las bolas se liberan del reposo a una altura\(h_{i}\) sobre el suelo.

Estado A: las bolas apenas llegan al suelo con velocidad\(v_{a}=\sqrt{2 g h_{i}}\). Esto se desprende de\(\Delta E_{\text {mесh}}=0 \Rightarrow \Delta K=-\Delta U\). Por lo tanto\((1 / 2) m v_{a}^{2}-0=-m g \Delta h=m g h_{i} \Rightarrow v_{a}=\sqrt{2 g h_{i}}\)

Estado B: inmediatamente antes de la colisión de las bolas. La bola 2 ha chocado con el suelo y ha invertido dirección con la misma velocidad,\(v_{a}\) pero la bola 1 sigue moviéndose hacia abajo con la velocidad\(v_{a}\).

Estado C: inmediatamente después de la colisión de las bolas. Porque estamos asumiendo que la\(m_{2} \gg m_{1}\) bola 2 no cambia su velocidad a consecuencia de la colisión por lo que sigue moviéndose 2 hacia arriba con la velocidad\(v_{a}\). Como resultado de la colisión, la bola 1 se mueve hacia arriba con velocidad\(v_{b}\)

Estado Final: la bola 1 alcanza una altura máxima\(h_{f}=v_{b}^{2} / 2 g\) sobre el suelo. Esto de nuevo se deduce de\(\Delta K=-\Delta U \Rightarrow 0-(1 / 2) m v_{b}^{2}=-m g \Delta h=-m g h_{f} \Rightarrow h_{f}=v_{b}^{2} / 2 g\)

Elección del marco de referencia:

Como se indica en la pista anterior, esta colisión se analiza mejor a partir del marco de referencia de un observador que se mueve hacia arriba con velocidad\(v_{a}\) la velocidad de la bola 2 justo después de que rebotó con el suelo. En este marco inmediatamente, antes de la colisión, la bola 1 se mueve hacia abajo con una velocidad\(v_{b}^{\prime}\) que es el doble de la velocidad vista por un observador en reposo en el suelo (marco de referencia de laboratorio). \[v_{a}^{\prime}=2 v_{a} \nonumber \]

La masa de la bola 2 es mucho mayor que la masa de la bola 1,\(m_{2} \gg m_{1}\) Esto nos permite considerar que la colisión (entre los Estados B y C) equivale a que la bola 1 rebota en una pared dura, mientras que la bola 2 prácticamente no experimenta retroceso. De ahí que la bola 2 permanezca en reposo en el marco de referencia moviéndose hacia arriba\(\mathcal{V}_{a}\) con la velocidad con respecto al observador en reposo en el suelo. Antes de la colisión, la bola 1 tiene velocidad\(v_{a}^{\prime}=2 v_{a}\) Dado que no hay pérdida de energía cinética durante la colisión, el resultado de la colisión es que la bola 1 cambia de dirección pero mantiene la misma velocidad,\[v_{b}^{\prime}=2 v_{a} \nonumber \] Sin embargo, de acuerdo con un observador en reposo en el suelo, después de que la bola de colisión 1 se esté moviendo hacia arriba con velocidad\[v_{b}=2 v_{a}+v_{a}=3 v_{a} \nonumber \] Mientras rebota, la energía mecánica de la superbola más pequeña es constante (consideramos la superbola más pequeña y la Tierra como un sistema) de ahí que entre el Estado C y el Estado Final,\[\Delta K+\Delta U=0 \nonumber \] El cambio en la energía cinética es\[\Delta K=-\frac{1}{2} m_{1}\left(3 v_{a}\right)^{2} \nonumber \] El cambio en la energía potencial es\[\Delta U=m_{1} g h_{f} \nonumber \] Entonces la condición de que la energía mecánica sea constante (Ecuación (15.5.10)) es ahora\[-\frac{1}{2} m_{1}\left(3 v_{1 a}\right)^{2}+m_{1} g h_{f}=0 \nonumber \] Podemos reescribir la Ecuación (15.5.13) como\[m_{1} g h_{f}=9 \frac{1}{2} m_{1}\left(v_{a}\right)^{2} \nonumber \] Recordemos que también podemos usar el hecho de que la energía mecánica no cambia entre el Estado Inicial y el Estado A dando una ecuación similar a la Ecuación (15.5.14), \[m_{1} g h_{i}=\frac{1}{2} m_{1}\left(v_{a}\right)^{2} \nonumber \]Ahora sustituya la expresión por la energía cinética en la Ecuación (15.5.15) por la Ecuación (15.5.14) rindiendo\[m_{1} g h_{f}=9 m_{1} g h_{i} \nonumber \] Así la bola 1 alcanza una altura máxima\[h_{f}=9 h_{i} \nonumber \]