17.3: Torque

Definición de Torque sobre un Punto

Para entender la dinámica de un cuerpo rígido giratorio introduciremos una nueva cantidad, el torque. Dejar$F=\left|\overrightarrow{\mathbf{F}}_{P}\right|$ actuar una fuerza$\overrightarrow{\mathbf{F}}_{P}$ con magnitud en un punto P. Let$\overrightarrow{\mathbf{r}}_{S, P}$ Ser el vector del punto$S$ a un punto P, con magnitud$r=\left|\overrightarrow{\mathbf{r}}_{S, P}\right|$. El ángulo entre los vectores$\overrightarrow{\mathbf{r}}_{S, P}$ y$\overrightarrow{\mathbf{F}}_{p}$ es θ con$[0 \leq \theta \leq \pi]$ (Figura 17.9).

Figura 17.9 Torsión alrededor de un punto$S$ debido a una fuerza que actúa en un punto P

El par alrededor de un punto$S$ debido a la fuerza$\overrightarrow{\mathbf{F}}_{P}$ que actúa en P, se define por

$$\vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, P} \times \overrightarrow{\mathbf{F}}_{P} \nonumber$$

La magnitud del par alrededor de un punto$S$ debido a la fuerza$\overrightarrow{\mathbf{F}}_{P}$ que actúa en P, viene dada por

$$\tau_{S} \equiv\left|\vec{\tau}_{S}\right|=r F \sin \theta \nonumber$$

Las unidades SI para par son [Nm]. La dirección del par es perpendicular al plano formado por los vectores$\overrightarrow{\mathbf{r}}_{S, P}$ y$\overrightarrow{\mathbf{F}}_{P} \quad \text { (for } \left.[0<\theta<\pi]\right)$, y por definición apunta en la dirección de la unidad de vector normal al plano$\hat{\mathbf{n}}_{R H R}$ como se muestra en la Figura 17.10.

Figura 17.10 Dirección vectorial para el par

La Figura 17.11 muestra las dos formas diferentes de definir la altura y la base para un paralelogramo definido por los vectores$\overrightarrow{\mathbf{r}}_{S, P} \text { and } \overrightarrow{mathbf{F}}_{P}$.

Figura 17.11 Área del paralelogramo de par.

Dejar$r_{\perp}=r \sin \theta$ y$F_{\perp}=F \sin \theta$ ser el componente de la fuerza$\overrightarrow{\mathbf{F}}_{P}$ que es perpendicular a la línea que pasa del punto$S$ a P. (Recordemos que el ángulo θ tiene un rango de valores$0 \leq \theta \leq \pi$ así que ambos$r_{\perp} \geq 0 \text { and } F_{\perp} \geq 0$. Entonces el área del paralelogramo definida por$\overrightarrow{\mathbf{r}}_{S, P}$ y$\overrightarrow{\mathbf{F}}_{P}$ viene dada por

$$\text { Area }=\tau_{S}=r_{\perp} F=r F_{\perp}=r F \sin \theta \nonumber$$

Podemos interpretar la cantidad de la$r_{\perp}$ siguiente manera.

Figura 17.12 El brazo de momento alrededor del punto$S$ y la línea de acción de la fuerza que pasa por el punto P

Comenzamos por trazar la línea de acción de la fuerza$\overrightarrow{\mathbf{F}}_{P}$. Se trata de una línea recta que pasa por P, paralela a la dirección de la fuerza$\overrightarrow{\mathbf{F}}_{P}$. Dibuja una perpendicular a esta línea de acción que pasa por el punto$S$ (Figura 17.12). A la longitud de esta perpendicular,$r_{\perp}=r \sin \theta$, se le llama brazo de momento alrededor del punto$S$ de la fuerza$\overrightarrow{\mathbf{F}}_{P}$.

Debe tener en cuenta tres propiedades importantes del torque:

1. El par es cero si los vectores$\overrightarrow{\mathbf{r}}_{S, P}$ y$\overrightarrow{\mathbf{F}}_{P}$ son paralelos (θ = 0) o antiparalelos$(\theta=\pi)$.

2. El par es un vector cuya dirección y magnitud dependen de la elección de un punto$S$ sobre el cual se calcula el par.

3. La dirección del par es perpendicular al plano formado por los dos vectores,$\overrightarrow{\mathbf{F}}_{P}$ y$r=\left|\overrightarrow{\mathbf{r}}_{S, P}\right|$ (el vector desde el punto$S$ a un punto P).

Enfoque Alternativo para Asignar una Convención de Signos para Torque

En el caso de que todas las fuerzas$\overrightarrow{\mathbf{F}}_{i}$ y vectores de posición$\overrightarrow{\mathbf{r}}_{i, P}$ sean coplanares (o cero), podemos, en lugar de referirnos a la dirección del par, asignar un signo positivo o negativo puramente algebraico al par de acuerdo con la siguiente convención. Observamos que el arco en la Figura 17.13a circunda en sentido contrario a las agujas del reloj. (Las figuras 17.13a y 17.13b utilizan la suposición simplificadora, a efectos únicamente de la figura, de que los dos vectores en cuestión,$\overrightarrow{\mathbf{F}}_{P}$ y$\overrightarrow{\mathbf{r}}_{S, P}$ son perpendiculares. No se muestra el punto$S$ sobre el cual se calculan los pares.)

Figura 17.13 (a) Torsión positiva fuera del plano, (b) par positivo en plano

Podemos asociar con esta orientación en sentido antihorario un vector normal unitario de$\hat{\mathbf{n}}$ acuerdo con la regla de la derecha: rizar los dedos de la mano derecha en sentido contrario a las agujas del reloj y su pulgar derecho luego apuntará en la$\hat{\mathbf{n}}_{1}$ dirección (Figura 17.13a). El arco en la Figura 17.13b circunda en el sentido de las agujas del reloj, y asociamos esta orientación con la unidad normal$\hat{\mathbf{n}}_{2}$.

Es importante tener en cuenta que los términos “en el sentido de las agujas del reloj” y “en sentido antihorario” pueden ser diferentes para diferentes observadores. Por ejemplo, si el plano que contiene$\overrightarrow{\mathbf{F}}_{P} \text { and } \overrightarrow{\mathbf{r}}_{S, P}$ es, horizontal, un observador por encima del plano y un observador debajo del plano no estarían de acuerdo en los dos términos. Para un plano vertical, las direcciones que dos observadores en lados opuestos del plano serían imágenes especulares entre sí, y así nuevamente los observadores no estarían de acuerdo.

1. Supongamos que elegimos en sentido antihorario como positivo. Luego asignamos un signo positivo para el componente del par cuando el par está en la misma dirección que la unidad normal$\hat{\mathbf{n}}_{1}, \text { i.e. } \vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, P} \times \overrightarrow{\mathbf{F}}_{P}=+\left|\overrightarrow{\mathbf{r}}_{S, P}\right|\left|\overrightarrow{\mathbf{F}}_{P}\right| \hat{\mathbf{n}}_{l}$ (Figura 17.13a).

2. Supongamos que elegimos en sentido horario como positivo Luego asignamos un signo negativo para el componente del par en la Figura 17.13b porque el par se dirige opuesto a la normal de la unidad$\hat{\mathbf{n}}_{2}, \text { i.e. } \vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, P} \times \overrightarrow{\mathbf{F}}_{P}=-\left|\overrightarrow{\mathbf{r}}_{S, P}\right| \overrightarrow{\mathbf{F}}_{P} \mid \hat{\mathbf{n}}_{2}$.

Ejemplo 17.6 Torque y Producto Vectorial

Considera dos vectores$\overrightarrow{\mathbf{r}}_{P, F}=x \hat{\mathbf{i}}$ con$x>0$ y$\overrightarrow{\mathbf{F}}=F_{x} \hat{\mathbf{i}}+F_{z} \hat{\mathbf{k}}$ con$F_{x}>0 \text { and } F_{z}>0$ Calcular el par$\overrightarrow{\mathbf{r}}_{P, F} \times \overrightarrow{\mathbf{F}}$.

Solución: Calculamos el producto vectorial señalando que en una elección diestra de vectores unitarios,$\hat{\mathbf{i}} \times \hat{\mathbf{i}}=\overrightarrow{\mathbf{0}} \text { and } \hat{\mathbf{i}} \times \hat{\mathbf{k}}=-\hat{\mathbf{j}}$

$$\overrightarrow{\mathbf{r}}_{P, F} \times \overrightarrow{\mathbf{F}}=x \hat{\mathbf{i}} \times\left(F_{x} \hat{\mathbf{i}}+F_{z} \hat{\mathbf{k}}\right)=\left(x \hat{\mathbf{i}} \times F_{x} \hat{\mathbf{i}}\right)+\left(x \hat{\mathbf{i}} \times F_{z} \hat{\mathbf{k}}\right)=-x F_{z} \hat{\mathbf{j}} \nonumber$$

Porque$x>0 \text { and } F_{z}>0$ la dirección del producto vectorial está en la dirección y negativa.

Ejemplo 17.7 Cálculo del par

En la Figura 17.14, se aplica una fuerza de magnitud F a un extremo de una palanca de longitud L. ¿Cuál es la magnitud y dirección del par alrededor del punto S?

Figura 17.15 Sistema de coordenadas

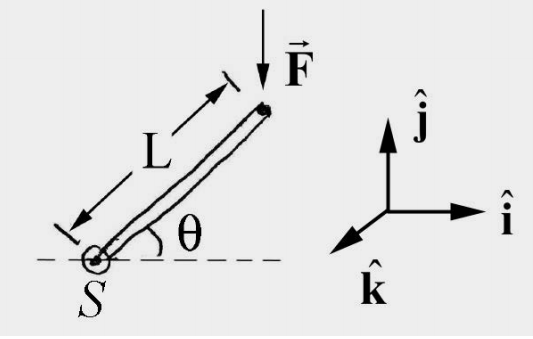
Solución: Elija unidades vectores de tal manera que$\hat{\mathbf{i}} \times \hat{\mathbf{j}}=\hat{\mathbf{k}}$, con$\hat{\mathbf{i}}$ apuntar a la derecha y$\hat{\mathbf{j}}$ apuntando hacia arriba (Figura 17.15). El par sobre el punto$S$ viene dado por$\vec{\tau}_{S}=\overrightarrow{\mathbf{r}}_{S, F} \times \overrightarrow{\mathbf{F}}$ dónde$\overrightarrow{\mathbf{r}}_{S F}=L \cos \theta \hat{\mathbf{i}}+L \sin \theta \hat{\mathbf{j}}$ y$\overrightarrow{\mathbf{F}}=-F \hat{\mathbf{j}}$ luego

$$\vec{\tau}_{S}=(L \cos \theta \hat{\mathbf{i}}+L \sin \theta \hat{\mathbf{j}}) \times-F \hat{\mathbf{j}}=-F L \cos \theta \hat{\mathbf{k}} \nonumber$$

Ejemplo 17.8 Torsión y Tobillo

Una persona de masa m se encuentra agachada con su peso distribuido uniformemente en ambas puntas de puntillas. El diagrama de fuerza de cuerpo libre en la parte esquelética del pie se muestra en la Figura 17.16. La fuerza normal$\overrightarrow{\mathbf{N}}$ actúa en el punto de contacto entre el pie y el suelo. En esta posición, la tibia actúa sobre el pie en el punto$S$ con una fuerza$\overrightarrow{\mathbf{F}}$ de magnitud desconocida$F=|\overrightarrow{\mathbf{F}}|$ y hace un ángulo desconocido$\beta$ con la vertical. Esta fuerza actúa sobre el tobillo a una distancia horizontal s desde el punto donde el pie entra en contacto con el piso. El tendón de Aquiles también actúa sobre el pie y se encuentra bajo una tensión considerable con magnitud$T \equiv|\overrightarrow{\mathbf{T}}|$ y actúa en un ángulo α con la horizontal como se muestra en la figura. El tendón actúa sobre el tobillo a una distancia horizontal b del punto$S$ donde la tibia actúa sobre el pie. Se puede ignorar el peso del pie. Que g sea la constante gravitacional. Calcular el par alrededor del punto$S$ debido a (a) la fuerza del tendón en el pie; (b) la fuerza de la tibia en el pie; (c) la fuerza normal del piso en el pie.

Figura 17.16 Diagrama de fuerza y sistema de coordenadas para tobillo

Solución: a) Primero calcularemos el par debido a la fuerza del tendón de Aquiles en el tobillo. La fuerza del tendón tiene la descomposición del vector$\overrightarrow{\mathbf{T}}=T \cos \alpha \hat{\mathbf{i}}+T \sin \alpha \hat{\mathbf{j}}$

Figura 17.17 Diagrama de par para la fuerza del tendón en el tobillo Figura 17.18 Diagrama de par para la fuerza normal en el tobillo$\overrightarrow{\mathbf{r}}_{S, N}$

El vector desde el punto$S$ hasta el punto de acción de la fuerza viene dado por$\overrightarrow{\mathbf{r}}_{S, T}=-b \hat{\mathbf{i}}$ (Figura 17.17). Por lo tanto, el par debido a la fuerza del tendón$\overrightarrow{\mathbf{T}}$ en el tobillo alrededor del punto$S$ es entonces

$$\vec{\tau}_{S, T}=\overrightarrow{\mathbf{r}}_{S, T} \times \overrightarrow{\mathbf{T}}=-b \hat{\mathbf{i}} \times(T \cos \alpha \hat{\mathbf{i}}+T \sin \alpha \hat{\mathbf{j}})=-b T \sin \alpha \hat{\mathbf{k}} \nonumber$$

(b) El diagrama de par para la fuerza normal se muestra en la Figura 17.18. El vector desde el punto$S$ hasta el punto donde la fuerza normal actúa sobre el pie viene dado por$\overrightarrow{\mathbf{r}}_{S, N}=(\hat{\mathbf{i}}-h \hat{\mathbf{j}})$. Debido a que el peso se distribuye uniformemente en los dos pies, la fuerza normal en un pie es igual a la mitad del peso, o$N=(1 / 2) m g$. Por lo tanto, la fuerza normal viene dada por$\overrightarrow{\mathbf{N}}=N \hat{\mathbf{j}}=(1 / 2) m g \hat{\mathbf{j}}$. Por lo tanto, el par de torsión de la fuerza normal alrededor del punto$S$ es

$$\vec{\tau}_{S, N}=\overrightarrow{\mathbf{r}}_{S, N} \times N \hat{\mathbf{j}}=((\hat{\mathbf{i}}-h \hat{\mathbf{j}}) \times N \hat{\mathbf{j}}=s N \hat{\mathbf{k}}=(1 / 2) s m g \hat{\mathbf{k}} \nonumber$$

(c) La fuerza$\overrightarrow{\mathbf{F}}$ que ejerce la tibia sobre el tobillo no aportará ninguna contribución al par alrededor de este punto$S$ ya que la fuerza de la tibia actúa en el punto$S$ y por lo tanto el vector$\overrightarrow{\mathbf{r}}_{S, F}=\overrightarrow{\mathbf{0}}$.