18.4: Ejemplos trabajados

Ejemplo 18.2 Varilla suspendida

Una varilla uniforme de longitud\(l=2.0 \mathrm{m}\) y masa\(m=4.0 \mathrm{kg}\) se articula a una pared en un extremo y se suspende de la pared por un cable que se une al otro extremo de la varilla en ángulo con respecto\(\beta=30^{\circ}\) a la varilla (ver Figura 18.7). Supongamos que el cable tiene masa cero. Hay una fuerza de contacto en el pivote de la varilla. Se desconoce la magnitud y dirección de esta fuerza. Una de las partes más difíciles de este tipo de problemas es introducir un ángulo para la fuerza de pivote y luego resolver ese ángulo si es posible. En este problema se resolverá por la magnitud de la tensión en el cable y la dirección y magnitud de la fuerza de pivote. a) ¿Cuál es la tensión en el cable? (b) ¿Qué ángulo forma la fuerza de pivote con la viga? c) ¿Cuál es la magnitud de la fuerza de pivote?

Figura 18.7 Ejemplo 18.2 Figura 18.8 Diagrama de fuerza y par.

Solución: a) El diagrama de fuerza se muestra en la Figura 18.8. Toma la\(\hat{\mathbf{i}}\) dirección positiva para estar a la derecha en la figura anterior, y toma la\(\hat{\mathbf{j}}\) dirección positiva para estar verticalmente hacia arriba. Las fuerzas sobre la varilla son: la fuerza gravitacional\(m \overrightarrow{\mathbf{g}}=-m g \hat{\mathbf{j}}\), que actúa en el centro de la varilla; la fuerza que ejerce el cable sobre la varilla,\(\overrightarrow{\mathbf{T}}=T(-\cos \beta \hat{\mathbf{i}}+\sin \beta \hat{\mathbf{j}})\) actuando en el extremo derecho de la varilla; y la fuerza de pivote\(\overrightarrow{\mathbf{F}}_{\text {pivot }}=F(\cos \alpha \hat{\mathbf{i}}+\sin \alpha \hat{\mathbf{j}})\), que actúa en el pivote del extremo izquierdo de la varilla. Si\(0<\alpha<\pi / 2\) la fuerza de pivote se dirige hacia arriba y hacia la derecha en la figura. Si\(0>\alpha>-\pi / 2\), la fuerza de pivote se dirige hacia abajo y hacia la derecha. No tenemos razón, en este punto, para esperar que\(\alpha\) sea en ninguno de los cuadrantes, pero debe ser en uno u otro.

estará en cualquiera de los cuadrantes, pero debe estar en uno u otro

\ [\ begin {array} {l}
0=-T\ cos\ beta+f\ cos\ alfa\\
0=-m g+t\ sin\ beta+f\ sin\ alfa
\ end {array}\ nonumber\]

Con respecto al punto de pivote, y tomando pares positivos para que sean en sentido antihorario, la fuerza gravitacional ejerce un par negativo de magnitud\(m g(l / 2)\) y el cable ejerce un par positivo de magnitud\(T l \sin \beta\). La fuerza de pivote no ejerce ningún par sobre el pivote. Establecer la suma de los pares igual a cero luego da

\ [\ begin {array} {l}
0=T l\ sin\ beta-m g (l/2)\
T=\ frac {m g} {2\ sin\ beta}
\ end {array}\ nonumber\]

Este resultado tiene muchas características que esperaríamos; proporcional al peso de la varilla e inversamente proporcional al seno del ángulo hecho por el cable con respecto a la horizontal. Insertar valores numéricos da

\[T=\frac{m g}{2 \sin \beta}=\frac{(4.0 \mathrm{kg})\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)}{2 \sin 30^{\circ}}=39.2 \mathrm{N} \nonumber \]

Hay muchas maneras de encontrar el ángulo\(\alpha\). Sustituyendo la ecuación (18.4.2) para la tensión en ambas ecuaciones de fuerza en la Ecuación (18.4.1) rendimientos

\ [\ begin {array} {l}
F\ cos\ alpha=T\ cos\ beta =( m g/2)\ cot\ beta\\
F\ sin\ alpha=m g-T\ sin\ beta=m g/2
\ end {array}\ nonumber\]

En la Ecuación (18.4.4), dividiendo una ecuación por la otra, vemos que\(\tan \alpha=\tan \beta, \alpha=\beta\)

Las fuerzas horizontales sobre la varilla deben cancelarse. La fuerza de tensión y la fuerza de pivote actúan con el mismo ángulo (pero en direcciones horizontales opuestas) y por lo tanto deben tener la misma magnitud,

\[F=T=39.2 \mathrm{N} \nonumber \]

Como alternativa, si no hubiéramos hecho las partes anteriores, podríamos encontrar pares sobre el punto donde el cable está unido a la pared. El cable no ejerce ningún par alrededor de este punto y el componente y de la fuerza de pivote tampoco ejerce par. El brazo de momento del componente x de la fuerza de pivote es\(l \tan \beta\) y el brazo de momento del peso es l/2. Equiparar las magnitudes de estos dos pares da

\[F \cos \alpha l \tan \beta=m g \frac{l}{2} \nonumber \]

equivalente a la primera ecuación de la Ecuación (18.4.4). De igual manera, evaluando pares alrededor del extremo derecho de la varilla, el cable no ejerce pares y el componente x de la fuerza de pivote no ejerce par. El brazo de momento del componente y de la fuerza de pivote es l y el brazo de momento del peso es l/2. Equiparar las magnitudes de estos dos pares da

\[F \sin \alpha l=m g \frac{l}{2} \nonumber \]

reproducir la segunda ecuación en la Ecuación (18.4.4). El objetivo de esta solución alternativa es mostrar que elegir un origen diferente (o incluso más de un origen) para eliminar una fuerza desconocida de las ecuaciones de par podría dar un resultado deseado de manera más directa.

Ejemplo 18.3 Persona de pie en una colina

Una persona se encuentra de pie sobre un cerro que está inclinado en ángulo\(\alpha\) con respecto a la horizontal (Figura 18.9). Las piernas de la persona están separadas por una distancia\(d\), con un pie cuesta arriba y otro cuesta abajo. El centro de masa de la persona se encuentra a una distancia\(h\) por encima del suelo, perpendicular a la ladera, a medio camino entre los pies de la persona. Supongamos que el coeficiente de fricción estática entre los pies de la persona y el cerro es lo suficientemente grande como para que la persona no resbale. a) ¿Cuál es la magnitud de la fuerza normal en cada pie? b) ¿Qué tan lejos deben estar los pies separados para que la fuerza normal en la parte superior del pie sea apenas cero? Este es el momento en que la persona comienza a rotar y caerse.

Figura 18.9 Persona de pie en colina Figura 18.10 Diagrama de fuerza de cuerpo libre para persona de pie en colina

Solución: El diagrama de fuerza sobre la persona se muestra en la Figura 18.10. Tenga en cuenta que las fuerzas de contacto se han descompuesto en componentes perpendiculares y paralelos a la ladera. También se muestra una selección de vectores unitarios y dirección positiva para el par. Aplicando la Segunda Ley de Newton a los dos componentes de la fuerza neta,

\[\hat{\mathbf{j}}: N_{1}+N_{2}-m g \cos \alpha=0 \nonumber \]

\[\hat{\mathbf{i}}: f_{1}+f_{2}-m g \sin \alpha=0 \nonumber \]

Estas dos ecuaciones implican que

\[N_{1}+N_{2}=m g \cos \alpha \nonumber \]

\[f_{1}+f_{2}=m g \sin \alpha \nonumber \]

Evaluar pares sobre el centro de masa,

\[h\left(f_{1}+f_{2}\right)+\left(N_{2}-N_{1}\right) \frac{d}{2}=0 \nonumber \]

La ecuación (18.4.10) se puede reescribir como

\[N_{1}-N_{2}=\frac{2 h\left(f_{1}+f_{2}\right)}{d} \nonumber \]

La sustitución de la ecuación (18.4.9) en la ecuación (18.4.11) rinde

\[N_{1}-N_{2}=\frac{2 h(m g \sin \alpha)}{d} \nonumber \]

Podemos resolver para sumando\(N_{1}\) las ecuaciones (18.4.8) y (18.4.12), y luego dividiendo por 2, rindiendo

\[N_{1}=\frac{1}{2} m g \cos \alpha+\frac{h(m g \sin \alpha)}{d}=m g\left(\frac{1}{2} \cos \alpha+\frac{h}{d} \sin \alpha\right) \nonumber \]

Del mismo modo, podemos resolver para\(N_{2}\) restando la Ecuación (18.4.12) de la Ecuación (18.4.8) y dividiendo por 2, rindiendo

\[N_{2}=m g\left(\frac{1}{2} \cos \alpha-\frac{h}{d} \sin \alpha\right) \nonumber \]

La fuerza normal\(N_{2}\) como se da en la Ecuación (18.4.14) desaparece cuando

\[\frac{1}{2} \cos \alpha=\frac{h}{d} \sin \alpha \nonumber \]

que se puede resolver para la distancia mínima entre las piernas,

\[d=2 h(\tan \alpha) \nonumber \]

Cabe señalar que no se utilizó ningún modelo específico para la fuerza de fricción, es decir, ningún coeficiente de fricción estática entró en el problema. Las dos fuerzas de fricción\(f_{1}\) y no\(f_{2}\) se determinaron por separado; sólo su suma ingresó a los cálculos anteriores.

Ejemplo 18.4 La rodilla

Un hombre de masa m = 70 kg está a punto de comenzar una carrera. Supongamos que el peso del corredor se distribuye equitativamente en ambas piernas. El ligamento rotuliano en la rodilla está unido a la tibia superior y corre sobre la rótula. Cuando se dobla la rodilla, una fuerza de tracción\(\overrightarrow{\mathbf{T}}\),, que el ligamento ejerce sobre la tibia superior, se dirige en un ángulo de\(\theta=40^{\circ}\) con respecto a la horizontal. El fémur ejerce una fuerza\(\overrightarrow{\mathbf{F}}\) sobre la tibia superior. El ángulo,\(\alpha\) que esta fuerza hace con la vertical variará y es una de las incógnitas a resolver. Supongamos que el ligamento está conectado a una distancia\(d=3.8 \mathrm{cm}\),, directamente por debajo del punto de contacto del fémur en la tibia. El punto de contacto entre el pie y el suelo es una\(s=3.6 \times 10^{1} \mathrm{cm}\) distancia de la línea vertical que pasa por el punto de contacto del fémur en la tibia. El centro de masa de la parte inferior de la pierna se encuentra a una\(x=1.8 \times 10^{1} \mathrm{cm}\) distancia de esta misma línea vertical. Supongamos que la masa\(m_{\mathrm{L}}\) de la parte inferior de la pierna es un 1/10 de la masa del cuerpo (Figura 18.11). (a) Encontrar la magnitud T de la fuerza\(\overrightarrow{\mathbf{T}}\) del ligamento rotuliano sobre la tibia. (b) Encontrar la dirección (el ángulo α) de la fuerza\(\overrightarrow{\mathbf{F}}\) del fémur sobre la tibia. c) Encontrar la magnitud F de la fuerza\(\overrightarrow{\mathbf{F}}\) del fémur sobre la tibia.

Figura 18.11 Ejemplo 18.4 Figura 18.12 Diagrama de par de fuerza para rodilla

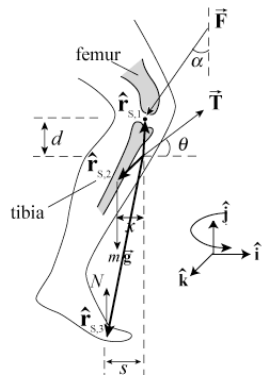
Soluciones: a) Elija el vector unitario\(\hat{\mathbf{i}}\) que se dirigirá horizontalmente hacia la derecha y\(\hat{\mathbf{j}}\) dirigido verticalmente hacia arriba. La primera condición para el equilibrio estático, Ecuación (18.1.1), que la suma de las fuerzas es cero se convierte en

\[\hat{\mathbf{i}}:-F \sin \alpha+T \cos \theta=0 \nonumber \]

\[\hat{\mathbf{j}}: N-F \cos \alpha+T \sin \theta-(1 / 10) m g=0 \nonumber \]

Debido a que el peso se distribuye uniformemente en los dos pies, la fuerza normal en un pie es igual a la mitad del peso, o

\[N=(1 / 2) m g \nonumber \]

La ecuación (18.4.18) se convierte en

\ [\ begin {array} {r}
\ hat {\ mathbf {j}} :( 1/2) m g-f\ cos\ alfa+t\ sin\ theta- (1/10) m g=0\\
(2/5) m g-f\ cos\ alfa+t\ sin\ theta=0
\ end {array}\ nonumber\]

El diagrama par-fuerza en la rodilla se muestra en la Figura 18.12. Elija el punto de acción del ligamento sobre la tibia como el punto\(S\) sobre el cual computar los pares. Obsérvese\(\overrightarrow{\mathbf{T}}\) que la fuerza de tracción, que ejerce el ligamento sobre la tibia superior no aportará ninguna contribución al par alrededor de este punto\(S\). Esto puede ayudar ligeramente en la elaboración de los cálculos. Elija en sentido contrario a las agujas del reloj como la dirección positiva para el par; esta es la dirección positiva\(\hat{\mathbf{k}}\). Entonces el par debido a la fuerza\(\overrightarrow{\mathbf{F}}\) del fémur sobre la tibia es

\[\vec{\tau}_{S, 1}=\overrightarrow{\mathbf{r}}_{S, 1} \times \overrightarrow{\mathbf{F}}=d \hat{\mathbf{j}} \times(-F \sin \alpha \hat{\mathbf{i}}-F \cos \alpha \hat{\mathbf{j}})=d F \sin \alpha \hat{\mathbf{k}} \nonumber \]

El par debido a la masa de la pierna es

\[\vec{\tau}_{S, 2}=\overrightarrow{\mathbf{r}}_{S, 2} \times(-m g / 10) \hat{\mathbf{j}}=\left(-x \hat{\mathbf{i}}-y_{L} \hat{\mathbf{j}}\right) \times(-m g / 10) \hat{\mathbf{j}}=(1 / 10) x m g \hat{\mathbf{k}} \nonumber \]

El par debido a la fuerza normal del suelo es

\[\vec{\tau}_{S, 3}=\overrightarrow{\mathbf{r}}_{S, 3} \times N \hat{\mathbf{j}}=\left(-s \hat{\mathbf{i}}-y_{N} \hat{\mathbf{j}}\right) \times N \hat{\mathbf{j}}=-s N \hat{\mathbf{k}}=-(1 / 2) s m g \hat{\mathbf{k}} \nonumber \]

(En las Ecuaciones (18.4.22) y (18.4.23),\(y_{L} \text { and } y_{N}\) se encuentran los desplazamientos verticales del punto τ donde el peso de la pierna y la fuerza normal con respecto al punto S; como puede verse, estas cantidades no entran directamente en los cálculos). La condición de que la suma de los pares sobre el punto se\(S\) desvanezca, Ecuación (18.1.2),

\[\vec{\tau}_{S, \text { total }}=\vec{\tau}_{S, 1}+\vec{\tau}_{S, 2}+\vec{\tau}_{S, 3}=\overrightarrow{0} \nonumber \]

se convierte

\[d F \sin \alpha \hat{\mathbf{k}}+(1 / 10) x m g \hat{\mathbf{k}}-(1 / 2) s m g \hat{\mathbf{k}}=\overrightarrow{\boldsymbol{0}} \nonumber \]

Las tres ecuaciones en las tres incógnitas se resumen a continuación:

\ [\ begin {array} {r}
-F\ sin\ alfa+T\ cos\ theta=0\\
(2/5) m g-F\ cos\ alfa+T\ sin\ theta=0\\
d F\ sin\ alpha+ (1/10) x m g- (1/2) s m g=0
\ end {array}\ nonumber\]

La ecuación de fuerza horizontal, la primera en (18.4.26), implica que

\[F \sin \alpha=T \cos \theta \nonumber \]

Sustituyendo esto en la ecuación de par, la tercera ecuación de (18.4.26), rinde

\[d T \cos \theta+(1 / 10) x m g-s(1 / 2) m g=0 \nonumber \]

Obsérvese que la Ecuación (18.4.28) es la ecuación que se habría obtenido si hubiéramos elegido el punto de contacto entre la tibia y el fémur como el punto sobre el cual determinar los pares. Si hubiéramos elegido este punto, habríamos guardado un paso algebraico menor. Podemos resolver esta Ecuación (18.4.28) para la magnitud T de la fuerza\(\overrightarrow{\mathbf{T}}\) del ligamento rotuliano sobre la tibia,

\[T=\frac{s(1 / 2) m g-(1 / 10) x m g}{d \cos \theta} \nonumber \]

Insertar valores numéricos en la ecuación (18.4.29),

\ [\ begin {aligned}
T & =( 70\ mathrm {kg})\ left (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ derecha)\ frac {\ izquierda (3.6\ times 10^ {-1}\ mathrm {m}\ right) (1/2) - (1/10)\ left (1.8\ times 10^ {-1}\ mathrm {m}\ derecha)} {\ izquierda (3.8\ veces 10^ {-2}\ mathrm {m}\ derecha)\ cos\ izquierda (40^ {\ circ}\ derecha)}\\
&=3. 8\ veces 10^ {3}\ mathrm {N}
\ final {alineado}\ nonumber\]

b) Ahora podemos resolver para la dirección\(\alpha\) de la fuerza\(\overrightarrow{\mathbf{F}}\) del fémur sobre la tibia de la siguiente manera. Reescribe las dos ecuaciones de fuerza en (18.4.26) como

\ [\ begin {array} {l}
F\ cos\ alfa =( 2/5) m g+t\ sin\ theta\\
F\ sin\ alpha=T\ cos\ theta
\ end {array}\ nonumber\]

Dividir estas ecuaciones rinde

\[\frac{F \cos \alpha}{F \sin \alpha}=\operatorname{cotan} \alpha=\frac{(2 / 5) m g+T \sin \theta}{T \cos \theta} \nonumber \]

Y así

\ [\ begin {array} {l}
\ alpha=\ nombreoperador {cotan} ^ {-1}\ izquierda (\ frac {(2/5) m g+t\ sin\ theta} {T\ cos\ theta}\ derecha)\
\ alpha=\ nombreoperador {cotan} ^ {-1}\ izquierda (\ frac {(2/5) (70\ mathrm {kg})\ izquierda (9.8\ mathrm {m}\ cdot\ mathrm {s} ^ {-2}\ derecha) +\ left (3.4\ times 10^ {3}\ mathrm {N}\ derecha)\ sin\ izquierda (40^ {\ circ}\ derecha)} {\ izquierda (3.4\ veces 10^ {3}\ mathrm {N}\ derecha)\ cos\ izquierda (40^ {\ circ}\ derecha)}\ derecha) =47^ {\ circ}
\ end {array}\ nonumber\]

c) Ahora podemos usar la ecuación de fuerza horizontal para calcular la magnitud F de la fuerza del fémur\(\overrightarrow{\mathbf{F}}\) sobre la tibia a partir de la Ecuación (18.4.27),

\[F=\frac{\left(3.8 \times 10^{3} \mathrm{N}\right) \cos \left(40^{\circ}\right)}{\sin \left(47^{\circ}\right)}=4.0 \times 10^{3} \mathrm{N} \nonumber \]

Tenga en cuenta que puede encontrar una expresión simbólica para\(\alpha\) que no implicara el cálculo numérico intermedio de la tensión. Esto es bastante complicado algebraicamente; básicamente, las dos últimas ecuaciones en (18.4.26) se resuelven para F y T en términos de\(\alpha, \theta\) y las otras variables (se sugiere la regla de Cramer) y los resultados se sustituyen por la primera de (18.4.26). La expresión resultante es

\ [\ begin {alineado}
\ cot\ alpha &=\ frac {(s/2-x/10)\ sin\ izquierda (40^ {\ circ}\ derecha) +\ izquierda ((2 d/5)\ cos\ izquierda (40^ {\ circ}\ derecha)} {(s/2-x/10)\ cos\ izquierda (40^ {\ circ}\ derecha)}\\
&=\ tan\ izquierda (40^ {\ circ}\ derecha) +\ frac {2 d/5} {s/2-x/10}
\ end {alineado}\ nonumber\]

lo que lleva al mismo resultado numérico,\(\alpha=47^{\circ}\)