23.4: Ejemplos trabajados

Ejemplo 23.3: Cilindro oscilante rodante sin deslizamiento

Acople un cilindro sólido de masa M y radio R a un resorte horizontal sin masa con constante de resorte k para que pueda rodar sin deslizarse a lo largo de una superficie horizontal. En el tiempo t, el centro de masa del cilindro se mueve con velocidad\(V_{c m}\) y el resorte se comprime vθ ,1 = ± 2gl (1− cosθ0). una distancia x de su longitud de equilibrio. ¿Cuál es el periodo de movimiento armónico simple para el centro de masa del cilindro?

Figura 23.9 Ejemplo 23.3

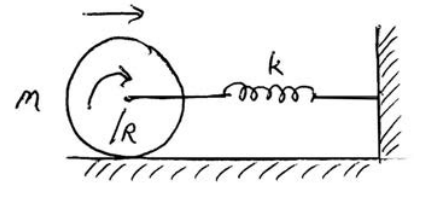
Solución: En el tiempo t, la energía del cilindro rodante y el sistema de resorte es

\[E=\frac{1}{2} M v_{c m}^{2}+\frac{1}{2} I_{c m}\left(\frac{d \theta}{d t}\right)^{2}+\frac{1}{2} k x^{2} \nonumber \]

donde x es la cantidad que el resorte ha comprimido,\(I_{c m}=(1 / 2) M R^{2}\), y porque está rodando sin deslizarse

\[\frac{d \theta}{d t}=\frac{V_{c m}}{R} \nonumber \]

Por lo tanto la energía es

\[E=\frac{1}{2} M V_{c m}^{2}+\frac{1}{4} M R^{2}\left(\frac{V_{c m}}{R}\right)^{2}+\frac{1}{2} k x^{2}=\frac{3}{4} M V_{c m}^{2}+\frac{1}{2} k x^{2} \nonumber \]

La energía es constante (ninguna fuerza no conservadora está trabajando en el sistema) por lo que

\[0=\frac{d E}{d t}=\frac{3}{4} 2 M V_{c m} \frac{d V_{c m}}{d t}+\frac{1}{2} k 2 x \frac{d x}{d t}=V_{c m}\left(\frac{3}{2} M \frac{d^{2} x}{d t^{2}}+k x\right) \nonumber \]

Debido a que no\(V_{c m}\) es cero la mayor parte del tiempo, el desplazamiento del resorte satisface una ecuación simple del oscilador armónico

\[\frac{d^{2} x}{d t^{2}}+\frac{2 k}{3 M} x=0 \nonumber \]

De ahí que el periodo sea

\[T=\frac{2 \pi}{\omega_{0}}=2 \pi \sqrt{\frac{3 M}{2 k}} \nonumber \]

Ejemplo 23.4: Tubo en U

Un tubo en U abierto en ambos extremos se llena con un fluido incompresible de densidad\(\rho\). El área transversal A del tubo es uniforme y la longitud total del fluido en el tubo es L. Se utiliza un pistón para deprimir la altura de la columna de líquido en un lado por una distancia\(x_{0}\) (elevando el otro lado por la misma distancia) y luego se retira rápidamente (Figura 23.10). ¿Cuál es la frecuencia angular del movimiento armónico simple subsiguiente? Olvida cualquier fuerza resistiva y en las paredes del tubo en U.

Figura 23.11 Diagrama de energía para el agua

Solución: Utilizaremos la conservación de la energía. Primero elige como cero para la energía potencial gravitacional en la configuración donde los niveles de agua son iguales en ambos lados del tubo. Cuando el pistón de un lado deprime el fluido, éste se eleva por el otro. En un instante dado en el tiempo cuando una porción del fluido de masa\(\Delta m=\rho A x\) está a una altura x por encima de la altura de equilibrio (Figura 23.11), la energía potencial del fluido viene dada por

\[U=\Delta m g x=(\rho A x) g x=\rho \operatorname{Ag} x^{2} \nonumber \]

En ese mismo instante todo el fluido de longitud L y masa\(m=\rho A L\) se mueve con velocidad v, por lo que la energía cinética es

\[K=\frac{1}{2} m v^{2}=\frac{1}{2} \rho A L v^{2} \nonumber \]

Así la energía total es

\[E=K+U=\frac{1}{2} \rho A L v^{2}+\rho A g x^{2} \nonumber \]

Al descuidar la fuerza resistiva, la energía mecánica del fluido es constante. Por lo tanto

\[0=\frac{d E}{d t}=\rho A L v \frac{d v}{d t}+2 \rho \operatorname{Ag} x \frac{d x}{d t} \nonumber \]

Si solo consideramos la parte superior del fluido por encima de la posición de equilibrio en el brazo derecho en la Figura 23.13, reescribimos la Ecuación (23.4.10) como

\[0=\frac{d E}{d t}=\rho A L v_{x} \frac{d v_{x}}{d t}+2 \rho A g x \frac{d x}{d t} \nonumber \]

donde\(v_{x}=d x / d t\). Ahora reescribimos la condición energética usando\(d v_{x} / d t=d^{2} x / d t^{2}\) como

\[0=v_{x} \rho A\left(L \frac{d^{2} x}{d t^{2}}+2 g x\right) \nonumber \]

Esta condición se cumple cuando\(v_{x}=0\) es decir, la condición de equilibrio o cuando

\[0=L \frac{d^{2} x}{d t^{2}}+2 g x \nonumber \]

Esta última condición se puede escribir como

\[\frac{d^{2} x}{d t^{2}}=-\frac{2 g}{L} x \nonumber \]

Esta última ecuación es la ecuación simple del oscilador armónico. Usando las mismas técnicas matemáticas que usamos para el sistema de bloque de resorte, la solución para la altura del fluido por encima de la posición de equilibrio viene dada por

\[x(t)=B \cos \left(\omega_{0} t\right)+C \sin \left(\omega_{0} t\right) \nonumber \]

donde

\[\omega_{0}=\sqrt{\frac{2 g}{L}} \nonumber \]

es la frecuencia angular de oscilación. El componente x de la velocidad del fluido en el lado derecho del tubo en U viene dado por

\[v_{x}(t)=\frac{d x(t)}{d t}=-\omega_{0} B \sin \left(\omega_{0} t\right)+\omega_{0} C \cos \left(\omega_{0} t\right) \nonumber \]

Los coeficientes B y C están determinados por las condiciones iniciales. A\(t=0\) la altura del fluido es\(x(t=0)=B=x_{0}\). A\(t=0\), la velocidad es cero así\(v_{x}(t=0)=\omega_{0} C=0\), de ahí\(C=0\). La altura del fluido por encima de la posición de equilibrio en el lado derecho del tubo en U en función del tiempo es así

\[x(t)=x_{0} \cos (\sqrt{\frac{2 g}{L}} t) \nonumber \]