27.3: Presión en un Fluido

Cuando se aplica una fuerza de cizallamiento a la superficie del fluido, el fluido sufrirá flujo. Cuando un fluido es estático, la fuerza sobre cualquier superficie dentro del fluido debe ser perpendicular (normal) a cada lado de esa superficie. Esta fuerza se debe a las colisiones entre las moléculas del fluido en un lado de la superficie con moléculas en el otro lado. Para un fluido estático, estas fuerzas deben sumar a cero. Considere una pequeña porción de un fluido estático que se muestra en la Figura 27.1. Esa porción del fluido se divide en dos partes, que designaremos 1 y 2, por un pequeño elemento matemático de superficie compartida\(S\) de área\(A_{S}\). La fuerza\(\overrightarrow{\mathbf{F}}_{1,2}(S)\) sobre la\(S\) superficie de la región 2 debido a las colisiones entre las moléculas de 1 y 2 es perpendicular a la superficie.

Figura 27.1: Fuerzas sobre una superficie dentro de un fluido

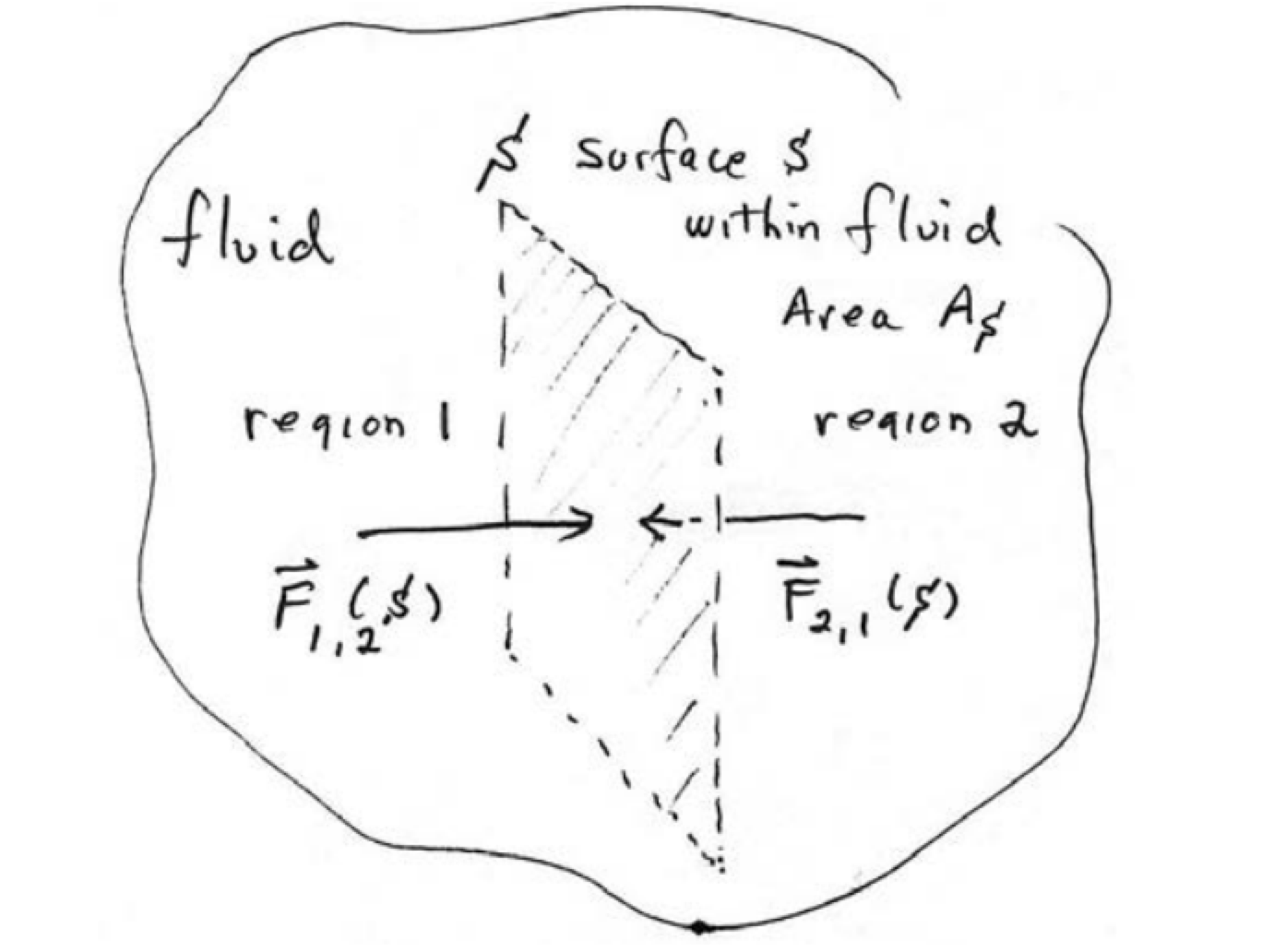
La fuerza\(\overrightarrow{\mathbf{F}}_{21}(S)\) sobre la superficie de la región 1 debido a las colisiones entre las moléculas de 1 y 2 por la Tercera Ley de Newton satisface\[\overrightarrow{\mathbf{F}}_{1,2}(S)=-\overrightarrow{\mathbf{F}}_{2,1}(S) \nonumber \] Denotar la magnitud de estas fuerzas que forman este par de interacción por\[F_{\perp}(S)=\left|\overrightarrow{\mathbf{F}}_{1,2}(S)\right|=\left|\overrightarrow{\mathbf{F}}_{2,1}(S)\right| \nonumber \] Definir la presión hidrostática en aquellos puntos dentro del fluido que se encuentran en el superficie\(S\) por\[P \equiv \frac{F_{\perp}(S)}{A_{S}} \nonumber \] La presión en un punto de la superficie\(S\) es el límite\[P=\lim _{A_{S} \rightarrow 0} \frac{F_{\perp}(S)}{A_{S}} \nonumber \] Las unidades SI para la presión son\(\mathrm{N} \cdot \mathrm{m}^{-2}\) y se llama el pascal (Pa), donde\[1 \mathrm{Pa}=1 \mathrm{N} \cdot \mathrm{m}^{-2}=10^{-5} \mathrm{bar} \nonumber \] La presión atmosférica en un punto es la fuerza por unidad de área ejercida sobre una superficie pequeña que contiene ese punto por el peso del aire por encima de esa superficie. En la mayoría de las circunstancias, la presión atmosférica se aproxima estrechamente por la presión hidrostática causada por el peso del aire por encima del punto de medición. En una superficie determinada, las áreas de baja presión tienen menos masa atmosférica por encima de su ubicación, mientras que las áreas de alta presión tienen más masa atmosférica por encima de su ubicación. Asimismo, a medida que aumenta la elevación, hay menos masa atmosférica superpuesta, por lo que la presión atmosférica disminuye con el aumento de la elevación. En promedio, una columna de aire de un centímetro cuadrado de sección transversal, medida desde el nivel del mar hasta la cima de la atmósfera, tiene una masa de aproximadamente 1.03 kg y un peso de aproximadamente 10.1 N. (Una columna de una pulgada cuadrada de sección transversal tendría un peso de aproximadamente 14.7 lbs, o aproximadamente 65.4 N). La atmósfera estándar [atm] es una unidad de presión tal que\[1 \mathrm{atm}=1.01325 \times 10^{5} \mathrm{Pa}=1.01325 \mathrm{bar} \nonumber \]