4.10: La cima

Hemos clasificado los cuerpos sólidos técnicamente como cimas simétricas, asimétricas, esféricas y lineales, según los tamaños relativos de sus principales momentos de inercia. En esta sección, o al menos en el título de esta sección, me refiero a “top” en el sentido no técnico del juguete del niño —es decir, un cuerpo simétrico, apuntado en un extremo, girando alrededor de su eje de simetría, con el extremo puntiagudo en el suelo o sobre una mesa. Técnicamente, es un “top simétrico pesado con un punto fijo”.

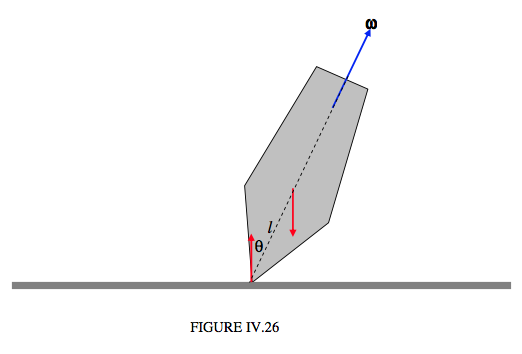
La he dibujado es la Figura IV.26, girando alrededor de su eje de simetría, que hace un ángulo\( \theta\) con la vertical. La distancia entre el centro de masa y el punto de contacto con la mesa es l. Tiene un par de fuerzas que actúan sobre ella, su peso y la reacción igual y opuesta de la mesa. En la Figura IV.27, sustituyo estas dos fuerzas por un par\( \boldsymbol\tau \), que es de magnitud\( Mgl\sin\theta\).

Tenga en cuenta que, dado que existe un par externo que actúa sobre el sistema, el vector de momento angular no es fijo.

Antes de involucrarnos demasiado con numerosas Ecuaciones, dediquemos un poco de tiempo a describir cualitativamente el movimiento de una cima, y también describiendo los diversos sistemas de coordenadas y ángulos que estaremos discutiendo. Primero, estaremos haciendo uso de un conjunto de coordenadas fijas en el espacio. Dejaremos que el origen\( O\) de las coordenadas esté en el punto (fijo) donde la punta de la parte superior toque la mesa. El eje\( Oz\) apunta verticalmente hasta el cenit. Los\( Oy\) ejes\( Ox\) y están en el plano (horizontal) de la mesa. Su orientación exacta no es muy importante, pero supongamos que\( Ox\) apunta hacia el sur, y\( Oy\) apunta hacia el este. \( Oxyz\)entonces constituye un conjunto diestro. También haremos uso de un conjunto de ejes fijos al cuerpo, a los que solo me referiré por el momento como 1, 2 y 3. El eje 3 es el eje de simetría de la parte superior. Los ejes 1 y 2 son perpendiculares a éste. Sus posiciones exactas no son muy importantes, pero supongamos que el plano 31 pasa por un pequeño punto de tinta que has marcado en el costado de la parte superior, y que el sistema 123 constituye un conjunto diestro.

Vamos a describir la orientación de la parte superior en algún instante por medio de los tres ángulos eulerianos\( \theta\),\( \phi\) y\( \psi\) (ver Figura IV.28). El eje de simetría de la parte superior está representado por la flecha pesada, y se inclina en ángulo\( \theta\) con respecto al\( z\) eje. Me referiré a un plano normal al eje de simetría como el “ecuador” de la parte superior, y está inclinado\( \theta\) hacia el\( xy\) plano. El nodo ascendente del ecuador en el\( xy\) plano -tiene un acimut\( \phi\), y\( \psi\) es la distancia angular del eje 1 desde el nodo. El acimut del eje de simetría de la parte superior es\( \phi\) - 90 ° =\( \phi\) + 270°.

Ahora permítanme anticipar un poco y describir el movimiento de la parte superior mientras está girando y sujeta al par descrito anteriormente.

El eje de simetría de la parte superior va a preceder alrededor del\( z\) eje -eje, a una velocidad que se describirá como\( \dot{\phi} \). Excepto bajo algunas condiciones (que eventualmente describiré) este movimiento precessional es laico. Eso significa que eso\( \phi\) aumenta todo el tiempo —no oscila de un lado a otro. Sin embargo, el eje de simetría no permanece en un ángulo constante con el\( z\) eje. Oscila, o asiente, hacia arriba y hacia abajo entre dos límites. A esta moción se le llama nutación (latín: nutare, asentir). Uno de nuestros objetivos será tratar de encontrar la tasa de nutación\( \dot{\phi} \) y encontrar el periodo y amplitud de la nutación.

Puede parecer como si la parte superior estuviera girando alrededor de su eje de simetría, pero esto no es así del todo. Si el vector de velocidad angular estuviera exactamente a lo largo del eje de simetría, permanecería ahí, y no habría precesión ni nutación, y esto no puede ser mientras haya un par que actúe en la parte superior. Una excepción sería si la parte superior estuviera girando verticalmente (\( \theta\)= 0), cuando no habría par que actuara sobre ella. De hecho, la parte superior puede hacer eso, excepto que, a menos que la capota esté girando bastante rápido, esta situación es inestable, y la parte superior se alejará de su posición vertical ante la menor perturbación. A altas velocidades de centrifugado, sin embargo, dicho movimiento es estable, y de hecho uno de nuestros objetivos debe ser determinar la menor velocidad angular alrededor del eje de simetría tal movimiento es estable.

Sin embargo, como se mencionó, a menos que la parte superior esté girando verticalmente, el vector no\( \omega\) se dirige a lo largo del eje de simetría. Llamaremos a los tres componentes de\( \omega\) a lo largo de los tres ejes fijos del cuerpo\( \omega_{1}\),\( \omega_{2}\) y\( \omega_{3}\), el último de estos es el componente de\( \omega\) a lo largo del eje de simetría. Una de las cosas que descubriremos cuando procedamos con el análisis es que\( \omega_{3}\) permanece constante a lo largo del movimiento. También, deberías ser capaz de distinguir entre\( \omega_{3}\) y\( \dot{\psi} \). Estos no son lo mismo, por el movimiento del nodo. De hecho probablemente lo entenderás\( \psi = \omega_{3} - \dot{\phi} \cos \theta \). En efecto, ya hemos derivado las relaciones entre el componente del vector de velocidad angular y la velocidad de cambio de los ángulos eulerianos — ver Ecuaciones 4.2.1 ,2 y 3. Estaremos haciendo uso de estas relaciones en lo que sigue.

Para analizar el movimiento de la cima, voy a hacer uso de las Ecuaciones de movimiento de Lagrange para un sistema conservador. Si estás familiarizado con las ecuaciones de Lagrange, esto será sencillo. Si no lo eres, tal vez prefieras saltarte esta sección hasta que te hayas familiarizado con la mecánica lagrangiana en el Capítulo 13. Sin embargo, introduje brevemente la Ecuación de Lagrange en la Sección 4.4, en la que la Ecuación de movimiento de Lagrange se dio como

\[ \ \frac{d}{dt} \left(\frac{\partial T}{\partial \dot{q}_{j}}\right) - \left(\frac{\partial T}{\partial \dot{q}_{j}}\right) = P_{j}. \tag{4.10.1}\label{eq:4.10.1} \]

Aquí\(T\) está la energía cinética del sistema. \(P_j\)es la fuerza generalizada asociada a la coordenada generalizada\(q_j\). Si la fuerza es una fuerza conservadora, entonces se\(P_j\) puede expresar como el negativo de la derivada de una función de energía potencial:

\[ \ P_{j} = - \left(\frac{\partial V}{\partial q_{j}}\right) \tag{4.10.2}\label{eq:4.10.2} \]

Así tenemos la Ecuación de movimiento de Lagrange para un sistema de fuerzas conservadoras

\[ \ \frac{d}{dt}\left(\frac{\partial V}{\partial \dot{q_{j}}}\right) - \frac{\partial V}{\partial q_{j}} = - \frac{\partial V}{\partial q_{j}} \tag{4.10.3}\label{eq:4.10.3} \]

Así, al resolver problemas en la dinámica lagrangiana, la primera línea en nuestro cálculo es anotar una expresión para la energía cinética. Comienza la primera línea: “\( T = ...\)”.

En el presente problema, la energía cinética es

\[ \ T = \frac{1}{2} I_{1}(\omega^{2}_{1} + \omega^{2}_{2}) + \frac{1}{2} I_{3}\omega^{2}_{3} \tag{4.10.4}\label{eq:4.10.4} \]

Aquí los subíndices se refieren a los ejes principales, siendo 3 el eje de simetría. Los ángulos eulerianos\( \theta\) y\( \phi\) son distancia cenital y azimut respectivamente del eje de simetría con respecto a los ejes fijos de laboratorio (espacio fijo). El ángulo euleriano\( \psi\) se mide alrededor del eje de simetría. Los componentes de la velocidad angular están relacionados con las tasas de cambio de los ángulos eulerianos por fórmulas previamente derivadas (Ecuaciones 4.2.1,2,3), por lo que el\( \dot{\theta} , \dot{\phi} \) y\( \dot{\psi } \).

\[ \ T = \frac{1}{2} I_{1}(\dot{\theta}^{2} + \dot{\phi}^{2} \sin^{2} \theta) + \frac {1}{2} I_{3} (\dot{\psi} + \dot{\phi} \cos \theta)^{2} \tag{4.10.5}\label{eq:4.10.5} \]

La energía potencial es

\[ \ V = Mgl\cos\theta + constant. \tag{4.10.6}\label{eq:4.10.6} \]

Habiendo escrito las expresiones para las energías cinéticas y potenciales en términos de los ángulos eulerianos, ahora estamos en condiciones de aplicar las Ecuaciones Lagrangianas de movimiento 4.10.3 para cada una de las tres coordenadas. Empezaremos con la coordenada\( \phi\). La ecuación lagrangiana es

\[ \ \frac{d}{dt}(\frac{\partial T}{\partial \dot{\phi}}) - \frac{\partial T}{\partial \phi} = -\frac{\partial V}{\partial \phi} \tag{4.10.7}\label{eq:4.10.7} \]

Vemos eso\( \frac{\partial T}{\partial \phi} \) y\( \frac{\partial V}{\partial \phi} \) son cada uno cero, así que eso\( \frac{d}{dt}\frac{\partial T}{\partial \phi} = 0, \) o\( \frac{\partial T}{\partial \phi} \) = constante. Esto tiene las dimensiones del momento angular, así que llamaré a la constante L ₁. Al evaluar la derivada\( \frac{\partial T}{\partial \phi} \), obtenemos para la Ecuación Lagrangiana en\( \phi\):

\[ \ I_{1} \dot{\phi}sin^{2}\theta + I_{3} \dot{\phi}\cos^{2}\theta+ I_{3} \dot{\psi}\cos\theta = L_{1} \tag{4.10.8}\label{eq:4.10.8} \]

Dejaré al lector para que realice exactamente el mismo procedimiento con la coordenada\( \psi\). Rápidamente concluirás que\( \frac{\partial T}{\partial \psi} \) = constante, que tiene las dimensiones del momento angular, así llámalo\( L_{3}\), y luego llegarás a lo siguiente para la Ecuación Lagrangiana en\( \psi\):

\[ \ I_{3}(\psi + \dot{\phi} \cos \theta) = L_{3} \tag{4.10.9}\label{eq:4.10.9} \]

Pero la expresión entre paréntesis es igual a\( \omega_{3}\) (ver Ecuación 4.2.3, aunque ya la hemos usado en la Ecuación\( \ref{eq:4.10.5}\)), por lo que obtenemos el resultado de que\( \omega_{3}\), el componente de la velocidad angular alrededor del eje de simetría, es constante durante el movimiento de la parte superior. Probablemente valdría la pena el tiempo del lector en este punto para volver a distinguir cuidadosamente en su mente la diferencia entre\( \omega_{3}\) y\( \dot{\psi} \).

Eliminar\( \dot{\psi} \) de ecuaciones\( \ref{eq:4.10.8}\) y\( \ref{eq:4.10.9}\):

\[ \ \dot{\phi} = \frac{L_{1} - L_{3} cos \theta} {I_{1}\sin^{2}\theta} \tag{4.10.10}\label{eq:4.10.10} \]

Esta Ecuación nos dice cómo varía la tasa de precesión a\( \theta\) medida que la parte superior asiente o nuta hacia arriba y hacia abajo.

También podríamos eliminar\( \dot{\phi} \) de Ecuaciones\( \ref{eq:4.10.8}\) y\( \ref{eq:4.10.9}\):

\[ \ \dot{\psi} = \frac{L_{3}}{I_{3}} - \frac{(L_{1}-L_{3} \cos\theta)\cos\theta}{I_{1}\sin^{2}\theta} \tag{4.10.11}\label{eq:4.10.11} \]

La Ecuación Lagrangiana en\( \theta\) es un poco más complicada, pero podemos obtener una tercera Ecuación de movimiento a partir de la constancia de la energía total:

\[ \ \frac{1}{2} I_{1} (\dot{\theta}^{2} + \dot{\phi}^{2}\sin^{2}\theta) + \frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi}\cos\theta)^{2}+Mgl\cos\theta = E. \tag{4.10.12}\label{eq:4.10.12} \]

Podemos eliminar\( \dot{\phi} \) y\( \dot{\psi} \) a partir de esto, usando Ecuaciones\( \ref{eq:4.10.10}\) y\( \ref{eq:4.10.11}\), para obtener una Ecuación en\( \theta\) y el tiempo solamente. Después de un poco de álgebra, obtenemos

\[ \ \dot{\theta}^{2} = A - B\cos\theta - \left(\frac{L_{1}-L_{3} \cos\theta}{I_{1} \sin\theta}\right)^{2}, \tag{4.10.13}\label{eq:4.10.13} \]

donde

\[ \ A = \frac{1}{I_{1}}\left(2E - \frac{L^{2}_{3}}{I_{3}}\right) \tag{4.10.14}\label{eq:4.10.14} \]

y

\[ \ B = \frac{2Mgl}{I_{1}} \tag{4.10.15}\label{eq:4.10.15} \]

Los puntos de inflexión en el\( \theta\) -movimiento (es decir, la nutación) ocurren donde\( \dot{\theta} = 0\). Esto resulta (¡después de un poco de álgebra! — pero bastante sencillo de todos modos) en una Ecuación cúbica en\( c = \cos\theta\):

\[ \ a_{0} = a_{1}c + a_{2}c^{2} + Bc^{3} = 0 \tag{4.10.16}\label{eq:4.10.16} \]

donde

\[ \ a_{0} = A - \left(\frac{L_{1}}{I_{1}}\right)^{2} = \frac{2E}{I_{1}} - \frac{L_{3}^{2}}{I_{1}I_{3}}- \frac{L_{1}^{2}}{I_{1}^{2}}, \tag{4.10.17}\label{eq:4.10.17} \]

\[ \ a_{1} = \frac{2L_{1}L_{3}}{I^{2}_{1}} - B = \frac{2L_{1}L_{3}}{I^{2}_{1}} - \frac{2Mgl}{I_{1}} \tag{4.10.18}\label{eq:4.10.18} \]

y

\[ \ a_{2} = -A - \left(\frac{L_{3}}{I_{1}}\right)^{2} = -\left[\frac{2E}{I_{1}} - \frac{L^{2}_{3}}{I_{1}I_{3}}- \left(\frac{L_{3}}{I_{1}}\right)^{2}\right] \tag{4.10.19}\label{eq:4.10.19} \]

Ahora Ecuación\( \ref{eq:4.10.16}\) es una Ecuación cúbica en\( \cos \theta\) y tiene una raíz real o tres raíces reales, y en este último caso dos de ellas o las tres podrían ser iguales. También hay que tener en cuenta que\( \theta\) es real sólo si\( \cos \theta\) está en el rango −1 a+1. Estamos tratando de encontrar los límites de la nutación, así que esperamos que encontremos dos y sólo dos valores reales de\( \theta\). (Si la punta de la parte superior estuviera colocada encima de un punto, por ejemplo, si estuviera en la cima de la Torre Eiffel, en lugar de sobre una mesa horizontal, podría tener\( \theta\) > 90 °).

Para tratar de entender esto mejor, construí en mi mente un top algo similar en forma al representado en las Figuras IV.25 y 26, de unos 4 cm de diámetro, 7 cm de alto, hecho de latón. Para la forma y dimensiones particulares que imaginé, se trabajó para tener los siguientes parámetros, redondeados a dos figuras significativas:

M =0.53 kg l = 0.044 m I ₁ = 1.7×10 ⁻⁴ kg m ² I ₃ = 9.8×10 ⁻⁵ kg m ²

Pensé en girar la parte superior para que\( \omega_{3}\) (que, como hemos visto, permanece constante durante todo el movimiento) sea 250 rad s ^-1, y comenzaría la parte superior (\( \dot{\phi} = \dot{\theta} = 0 \)) a\( \theta\) = 30 °. y luego soltaría. Presumiblemente entonces inmediatamente comenzaría a caer, y 30 ° sería entonces el límite superior a la nutación. Queremos ver hasta dónde caerá antes de volver a asentir hacia arriba. Con\( \omega_{3}\) = 250 rad s ⁻¹ encontramos, de la Ecuación\( \ref{eq:4.10.9}\) que

\( L_{3}\)= 2.45 x 10 ^-2 Js

Además, estoy asumiendo que\( \dot{\phi} \) = 0 cuando\( \theta\) = 30 °, y Ecuación nos\( \ref{eq:4.10.10}\) dice que

L ₁ = 2.121762 x 10 ^-2 Js

Entonces con g = 9.8 m s ⁻², tenemos, de la Ecuación\( \ref{eq:4.10.15}\),

B = 2.688659 x 10 ³ s ^-2.

Mis condiciones iniciales son eso\( \dot{\phi} \) y\( \dot{\theta} \) son cada uno cero cuando\( \theta\) = 30°, y Ecuaciones\( \ref{eq:4.10.10}\) y\( \ref{eq:4.10.13}\) entre ellas nos dicen que\( A = B \cos\) 30°, para que

A = 2.328447 x 10 ³ s ^-2.

De las Ecuaciones 4.12.17, 18 y 19 tenemos ahora

a ₀ = -1.324989 x 10 ³ s ^-2

a1= +3.328586 x 10 ³ s ^-2

a2= -2.309834 x 10 ³ s ^-2

y ya tenemos

B = 2.688659 x 10 ³ s ^-2.

La “regla de signos” para Ecuaciones polinómicas, si estás familiarizado con ella, nos dice que no hay raíces reales negativas (es decir, no hay soluciones con\( \theta\) > 90 °), y de hecho si resolvemos la Ecuación cúbica\( \ref{eq:4.10.16}\) obtenemos

c = 0.824596, 0.866025, 6.9000406

El segundo de estos corresponde a\( \theta\) = 30 °, que ya sabíamos debe ser una solución. De hecho podríamos haber dividido la Ecuación\( \ref{eq:4.10.16}\) por\( c – \cos\) 30° para obtener una Ecuación cuadrática para las dos raíces restantes, pero quizás sea mejor resolver la Ecuación cúbica tal como está, para verificar que\( \cos\) 30° es efectivamente una solución, proporcionando así una verificación sobre el aritmética. La tercera solución no nos da una verdadera\( \theta\) (más bien esperábamos que esto sucediera). La segunda solución es el límite inferior de la nutación, correspondiente a\( \theta\) = 34 ° 27'.

Generalmente, sin embargo, la parte superior se nutará entre dos valores de\( \theta\). Llamemos a estos dos valores\( \alpha\) y\( \beta\),\( \alpha\) siendo el menor (más vertical) de los dos. Me referiré\( \theta = \alpha\) como el “límite superior” del movimiento, aunque\( \alpha<\beta\), ya que esto corresponde a la posición más vertical de la parte superior. Hemos mirado un poco el movimiento en\( \theta\); ahora veamos el movimiento adentro\( \phi\), comenzando con Ecuación\( \ref{eq:4.10.10}\):

\[ \ \dot{\phi}= \frac{L_{1}-L_{3}\cos \theta}{I_{1}\sin^{2}\theta} \tag{4.10.10.}\label{eq:4.10.10.} \]

Si las condiciones iniciales son tales que\( L_{1}>L_{3}\cos\alpha\) (y por tanto siempre mayores que\( L_{3}\cos\theta\)) siempre\( \hat{\phi} \) es positiva. El movimiento es entonces algo así como trato de ilustrar en la Figura IV.29

Este movimiento corresponde a una condición inicial en la que le das a la parte superior un empuje inicial en la dirección hacia adelante como lo indica la pequeña flecha azul. Si las condiciones iniciales son tales que\( \cos\alpha>\frac{L_{1}}{L_{3}}>\cos\beta\), el signo de\( \dot{\phi} \) es diferente en los límites superior e inferior. Así se ilustra en la Figura IV.30.

Este movimiento surgiría si inicialmente fueras a dar un pequeño empujón hacia atrás antes de soltar la parte superior, como lo indica la pequeña flecha azul.

Si las condiciones iniciales son tales que\( L_{1}=L_{3}\cos\alpha\), entonces\( \dot{\theta} \) y\( \dot{\phi} \) son cada uno cero en el límite superior de la nutación, y esta fue la situación en nuestro ejemplo numérico. Corresponde a simplemente dejar caer la parte superior cuando la sueltas, sin darle ni un empujón hacia adelante ni hacia atrás. Esto se ilustra en la Figura IV.31.

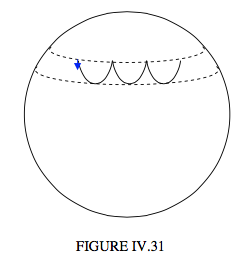
Como descubrimos haciendo nuestro ejemplo numérico, las condiciones iniciales\( \dot{\theta} = \dot{\phi} = 0 \) cuando\( \theta = \alpha\) conducen, en este tercer tipo de movimiento, a

\[ \ L_{1} = L_{3} \cos \alpha \tag{4.10.20}\label{eq:4.10.20} \]

y

\[ \ A = B \cos \alpha \tag{4.10.21}\label{eq:4.10.21} \]

En el caso Ecuación\( \ref{eq:4.10.13}\) se convierte

\[ \ \dot{\theta}^{2} = B(\cos \alpha - \cos \theta) - [\frac{L_{3}(\cos \alpha - \cos \theta)}{I_{1}\sin\theta}]^{2} \tag{4.10.22}\label{eq:4.10.22} \]

El límite inferior a la nutación (es decir, qué tan lejos cae la parte superior) se encuentra poniendo\( \theta = \beta\) cuando\( \dot{\theta} \) =0. Esto da la siguiente Ecuación cuadrática para\( \beta\):

\[ \cos^{2}\beta - \frac{L^{2}_{3}}{I^{2}_{1} B} \cos\beta + \frac{L^{2}_{3}\cos \alpha}{I_{1} \sin \theta} \tag{4.10.23}\label{eq:4.10.23} \]

En nuestro ejemplo numérico, esto es

\[ \cos^{2}\beta -7.725002 \cos \beta +5.690048 = 0, \tag{4.10.24}\label{eq:4.10.24} \]

que, naturalmente, tiene las mismas dos soluciones que obtuvimos cuando resolvimos la Ecuación cúbica, a saber, 0.824 596 y 6.900 406.

Recordando la definición de B (Ecuación\( \ref{eq:4.10.15}\)), vemos que la Ecuación se\( \ref{eq:4.10.23}\) puede escribir

\[ \ \cos \alpha - \cos\beta = \frac{2MglI_{1}}{L_{3}^{2}}\sin^{2}\beta, \tag{4.10.25}\label{eq:4.10.25} \]

de donde vemos que cuanto mayor\( L_{3}\), menor es la diferencia entre\( \alpha\) y\( \beta\) - es decir, cuanto menor es la amplituta de la nutación.

Ecuación\( \ref{eq:4.10.12}\), con la ayuda de Ecuaciones\( \ref{eq:4.10.10}\) y\( \ref{eq:4.10.11}\), se puede escribir:

\[ \ E - \frac{L^{2}_{3}}{2I_{3}}-\frac{1}{2}I_{1}\dot{\theta}^{2} = \frac{1}{2I_{1}}(L_{1}\csc\theta -L_{3} \cot \theta )^{2} + Mglcos\theta . \tag{4.10.26}\label{eq:4.10.26} \]

El lado izquierdo es la energía total menos las energías cinéticas de giro y nutación. Así, el lado derecho representa la energía potencial efectiva\( V_{e}(\theta)\) referida a un marco de referencia que está co-rotando con la precesión. El término no\( Mgl\sin\theta\) necesita explicación. Lo negativo de la derivada del primer término en el lado derecho sería la fuerza “ficticia” que “existe” en el marco de referencia corrotativo. La energía potencial efectiva\( V_{e}(\theta)\) viene dada por

\[ \ \frac{V_{e}(\theta)}{L_{1}^{2}/(2I_{1})}=[\csc\theta- (L_{3}/L_{1})\cot\theta]^{2} + \frac{2I_{1}Mgl\cos\theta}{L_{1}^{2}}. \tag{4.10.27}\label{eq:4.10.27} \]

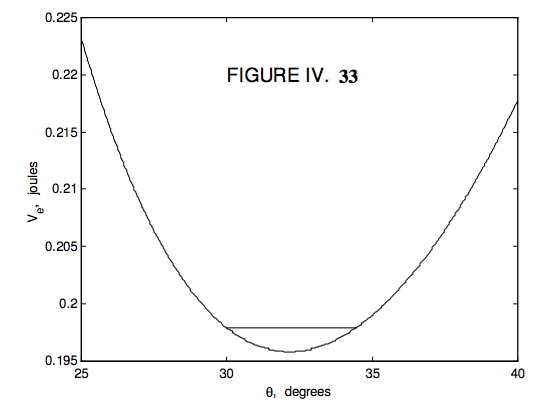
Dibujo\( V_{e}(\theta)\) en las Figuras IV.32 y 33 usando los valores que usamos en nuestro ejemplo numérico, es decir:

\[ \ V_{e}(\theta) = 1.32081(\csc\theta - 1.154701\cot\theta)^{2} +0.229536\cos\theta \qquad \text{joules}. \tag{4.10.28}\label{eq:4.10.28} \]

La Figura 32 se grafica hasta 90° (aunque como se mencionó anteriormente se podría ir más allá de esto si la parte superior no estuviera girando sobre una mesa horizontal), y la Figura 33 es una mirada cercana cercana a 2 al mínimo. Se puede ver que si\( E - L_{3}^{3}/(2I_{2}) = 0.1979 \) la energía potencial efectiva (que no puede ir más alta que esta, y alcanza este valor sólo cuando)\( \dot{\theta} \) = 0, los límites de nutación están entre 30 ° y 34 ° 24'. Para un dado\( L_{3}\), para una energía total mayor, los límites de nutación son correspondientemente más amplios. Pero para una energía total dada, cuanto mayor sea el componente\( L_{3}\) del momento angular, menor será la línea horizontal y más estrechos serán los límites de nutación. Si la parte superior pierde energía (por ejemplo, debido a la resistencia del aire, o fricción en el punto de contacto con la mesa), la E = línea constante se volverá más baja 2 e inferior, y la amplitud de la nutación será cada vez menor. Si\( E - L_{3}^{2}/(2I_{3}) \) es igual al valor mínimo de sólo\( V_{e}(\theta)\) hay una solución para\( \theta\), y no hay nutación. Para energía menor que esta, no hay valor estacionario de\( \theta\) y la parte superior cae.

Podemos encontrar la tasa de precesión regular verdadera simplemente de la siguiente manera, y esto a menudo se hace en libros introductorios.

En la Figura IV.34, el vector\( \bf{L}\) representa el momento angular en algún momento, y en un intervalo de tiempo\( \delta t\) posterior el cambio en el momento angular es\( \boldsymbol\delta { \bf L}\). El momento angular está cambiando debido al par externo, que es un vector horizontal de magnitud\( Mgl\sin\theta\) (recuérdese de la Figura XV .26 y 27). La tasa de cambio del momento angular viene dada por\( \bf{L} = \tau \). Con el tiempo\( \delta t\) la punta del vector\( \bf{L}\) se mueve a través de una “distancia”\( \tau \delta t\). Denotar por velocidad angular\( \boldsymbol\Omega\) precessional (cuya magnitud hemos llamado hasta ahora\( \dot{\phi}\)). La punta del vector de momento angular se mueve en un pequeño círculo de radio\( L\sin \theta\). Por lo tanto, eso lo vemos\( \tau = \Omega L \sin\theta\). Además,\( \tau \) es perpendicular a ambos\( \boldsymbol\Omega\) y\( \bf{L}\). Por lo tanto, en notación vectorial,

\[ \boldsymbol\tau = \boldsymbol\Omega \times { \bf L} \tag{4.10.29}\label{eq:4.10.29} \]

Obsérvese que la magnitud de\( \boldsymbol\tau \) es\( Mgl\sin\theta\) y la magnitud de\( \boldsymbol\Omega \times \bf{L}\) es\( \Omega L \sin\theta\), de manera que la tasa de precesión es

\[ \ \Omega = \frac{Mgl}{L} \tag{4.10.30}\label{eq:4.10.30} \]

y es independiente de\( \theta\).
Se puede seguir analizando la moción de un top casi indefinidamente, pero hay dos casos especiales que quizás valgan la pena señalar y que voy a describir.

Caso Especial I.\(L_{1} = L_{3}\).
En este caso, la ecuación\( \ref{eq:4.10.27}\) se convierte en

\[ \ \frac{V_{e}(\theta)}{Mgl}= C(csc\theta - cot\theta)^{2} +\cos\theta \tag{4.10.31}\label{eq:4.10.31} \]

donde

\[ \ C = \frac{L_{1}^{2}}{2MglI_{1}} \tag{4.10.32}\label{eq:4.10.32} \]

Puede ser bastante improbable que\(L_{1} = L_{3}\) exactamente, pero este caso es de interés en parte porque es excepcional en que\( V_{e}(0)\) no va al infinito; de hecho\( V_{e}(0)=Mgl\) sea cual sea el valor de\( C\). Intenta sustituir\( \theta\) = 0 en Ecuación\( \ref{eq:4.10.31}\) y ¡mira lo que obtienes! El lado derecho es de hecho 1, pero puede que tengas que trabajar un poco para llegar allí. La otra razón por la que este caso es de interés es que hace una introducción útil al caso II, lo cual no es imposiblemente improbable, es decir, que\( L_{1}\) es aproximadamente igual a\( L_{3}\), lo que lleva a moción de algún interés.

En la Figura IV.35, dibujo\( \frac{V_{e}(0)}{Mgl}\) para varios diferentes\( C\).

De las gráficas, parece que, si\( C \geq 2\), hay una posición de equilibrio, está a\( \theta\) = 0 ° (es decir, la parte superior es vertical), y el equilibrio es estable, Si\( C < 2\), hay dos posiciones de equilibrio: la posición vertical es inestable, y la otra posición de equilibrio es estable. Por lo tanto, si la capota está girando rápido (grande\( C\)) puede girar solo en posición vertical (un “top para dormir”), pero, a medida que la parte superior se ralentiza debido a la fricción y la resistencia al aire, la posición vertical se volverá inestable, y la parte superior caerá a un valor positivo de\( \theta\).

Estas deducciones son correctas, por\( \frac{dV_{e}}{d \theta} = 0\) resultados en

\[ \ 2C(1-cos\theta)^{2} = \sin^{4}\theta \tag{4.10.33}\label{eq:4.10.33} \]

Una solución es\( \theta = 0\), y una segunda diferenciación demostrará que ésta es estable o inestable según sea\( C\) mayor o menor que 2, aunque la segunda diferenciación es ligeramente tediosa, y se puede evitar. También podemos señalar que\( 1 − \cos\theta\) es un factor común de los dos lados de la Ecuación\( \ref{eq:4.10.33}\), y se puede dividir para producir una Ecuación cúbica en\( \cos\theta\):

\[ \ 2C-1-(2C+1)\cos\theta -\cos^{2}\theta - \cos^{3}\theta =0, \tag{4.10.34}\label{eq:4.10.34} \]

que podría resolverse para encontrar el segundo punto de equilibrio —pero eso de nuevo es un poco tedioso. Una forma menos tediosa podría ser tomar la raíz cuadrada de cada lado de la ecuación\( \ref{eq:4.10.33}\):

\[ \ \sqrt{2C}(1-\cos\theta)=1-\cos^{2}\theta \tag{4.10.35}\label{eq:4.10.35} \]

y luego dividir por el factor común (1 −\ cos θ) para obtener

\[ \cos \theta = \sqrt{2C} - 1, \tag{4.10.36}\label{eq:4.10.36} \]

lo que da un real\( \theta\) sólo si\( C \geq 2\). Tenga en cuenta también, si\(C = \frac{1}{2} \),\( \theta\) = 90 °.

Caso Especial II. \( L_{3} \approx L_{1}\).

En otras palabras,\( L_{1}\) y no\( L_{3}\) son muy diferentes. En la Figura IX.36 dibujo\( \frac{V_{e}(0)}{Mgl}\) para varios diferentes\( C\), para\( L_{3} = 1.01 L_{1}\).

Vemos que para un rango bastante grande de\( C\) más de 2 la posición de equilibrio estable es cercana a la vertical. A pesar de que la curva para\( C = 2\) tiene un mínimo muy amplio, el mínimo real es un poco menos de 17 °. (No he resuelto la posición exacta — se lo dejaré al lector.)