22.7: Apéndice A

Problemas Misceláneos

En este Apéndice ofrezco una serie de problemas aleatorios en la mecánica clásica. No están en ningún orden en particular —vienen tal como me ocurre pensar en ellos, y no necesariamente están relacionados con ninguno de los temas tratados en ninguno de los capítulos. Están destinados solo a ocuparte en esos días aburridos y lluviosos en los que no tienes nada mejor que hacer. Las soluciones estarán en el Apéndice B —salvo que cada vez que agrego algún problema nuevo al Apéndice A, que de vez en cuando, esperaré unos días antes de publicar las soluciones en el Apéndice B.

_________________________

Ejercicio\(\PageIndex{1}\)

Ningún libro sobre mecánica clásica está completo sin el problema de una escalera apoyada contra una pared. Aquí, entonces, hay un problema de escalera —salvo que no tiene nada que ver con la mecánica, y se pone aquí sólo por diversión. Es un problema sólo en geometría, sin embargo es uno que algunas personas al principio encuentran difícil. Incluso parece difícil tratar de encontrar una solución aproximada tratando de dibujarla con precisión a escala, y deliberadamente no la he dibujado a escala, ¡así que no puedes encontrar la respuesta simplemente tomando una regla y mediéndola!

Dos escaleras, de longitudes de 8 m y 10 m, se inclinan contra dos paredes como se muestra. Su punto de intersección se encuentra a 3 m sobre el suelo. ¿Cuál es la distancia entre las paredes?

Ejercicio\(\PageIndex{2}\)

Un péndulo de longitud\( l_{0}\), se pone en movimiento para que describa un cono como se muestra de ángulo semi-vertical\( \alpha\), describiendo el bob un círculo horizontal a velocidad angular\( \Omega\)

Demostrar que

\( \cos\alpha=\frac{\text{g}}{l_{0}\Omega^{2}}\).

Esto, por supuesto, es un problema muy trivial no digno de tu valía. Se da sólo como una introducción al siguiente problema.

Ejercicio\(\PageIndex{3a}\)

Una cuerda de péndulo pasa a través de una tabla como se muestra en la siguiente figura, de tal manera que, al bajar o elevar la tabla, se puede variar la longitud de la cuerda debajo de la tabla. La parte debajo del tablero es inicialmente de longitud\( l_{0}\), y se pone en movimiento como un péndulo cónico de manera que la velocidad angular y el ángulo semi vertical se relacionan por

\( \cos\ \alpha=\frac{\text{g}}{l_{0}\Omega^{2}}\).

A medida que el tablero se sube o baja (o alternativamente el péndulo se baja o se eleva) y en consecuencia la longitud\( l\) below the board is varied, the semivertical angle \( \theta\) cambiará y también lo hará la velocidad angular\( \omega\). (Los símbolos\( l_{0}\), \( \alpha\) y\( \Omega\) representan los valores iniciales de estas cantidades.)

Demostrar que

1. \( l^{3}\sin^{3}\theta\tan\theta\) is constant,
2. \( \omega^{3}\cot^{2}\theta\) is constant,
3. \( \omega^{3}(\omega l^{2}\ -\ \Omega l_{0}^{2}\sin^{2}\alpha)\) is constant.

Exercise \(\PageIndex{3b}\)

Start with the following initial conditions:

\( l_{0}\ =\ 50\ \text{cm} \qquad \Omega\ =\ 5\ \text{rad s}^{-1}\)

and assume that \( \text{g}\ =\ 9.8\ \text{m s}^{=2}\), so that \( \alpha\ =\ 38^{\circ}\ 22^{\prime}\).

1. Plot a graph of \( \theta\) (vertically) versus \( l\) (horizontally), for \( l\ =\ 0\) to 1 m. When \( l\) = 40 cm, what is \( \theta\) correct to one arcmin?
2. Plot a graph of \( \omega\) (vertically) versus \( \theta\) (horizontally), for \( \theta\) = 0 to 70^o.
3. Plot a graph of \( \omega\) (vertically) versus \( l\) (horizontally) for \( l\) = 16 cm to 1 m. When \( l\) = 60 cm, what is \( \omega\) correct to four significant figures?

________________

The next few problems involve a rod with its lower end in contact with a horizontal table and the rod falling over from an initial vertical (or inclined) position. There are several versions of this problem. The table could be smooth, so that the rod freely slips over the table. Or the lower end could be freely hinged at the table, so that the lower end does not move as the rod falls over. Or the table might be rough, so that the rod might or might not slip.

Exercise \(\PageIndex{4}\)

A uniform rod of mass \( m\) and length \( 2l\) is initially vertical with its lower end in contact with a smooth horizontal table. It is given an infinitesimal angular displacement from its initial position, so that it falls over. When the rod makes an angle \( \theta\) with the vertical, find:

The angular speed of the rod;

The speed at which the centre of the rod is falling;

The speed at which the lower end of the rod is moving;

Show that the speed of the lower end is greatest when \( \theta =\ 37^{\circ}\ 50^{\prime}\).

If the length of the rod is 1 metre, and \( \text{g}\) = 9.8 m s^-2, what is the angle \( \theta\) when the speed of the lower end is 1 m s^-1?

Exercise \(\PageIndex{5}\)

A uniform rod is initially vertical with its lower end smoothly hinged to a horizontal table. Show that, when the rod falls over, the reaction of the hinge upon the rod is vertical when the rod makes an angle 48^o 11' with the vertical, and is horizontal when the rod makes an angle 70^o 31' with the vertical.

Exercise \(\PageIndex{6}\)

A uniform rod of length 1 metre, with its lower end smoothly hinged to a horizontal table, is initially held at rest making an angle of 40^o with the vertical. It is then released. If \( \text{g}\) = 9.8 m s^-1, calculate its angular speed when it hits the table in a horizontal position (easy) and how long it takes to get there (not so easy).

Exercise \(\PageIndex{7}\)

A uniform rod is initially vertical with its lower end in contact with a rough horizontal table, the coefficient of friction being \( \mu\).

Show that:

Exercise \(\PageIndex{7a}\)

If \( \mu\) < 0.3706, the lower end of the rod must slip before the rod makes an angle \( \theta\) with the vertical of 35^o 05'.

Exercise \(\PageIndex{7b}\)

If \( \mu\) > 0.3706, the rod will not slip before \( \theta\) = 51^o 15', but it will certainly slip before \( \theta\) = 70^o 31' .

Exercise \(\PageIndex{7c}\)

If \( \mu\) = 0.25, at what angle \( \theta\) will the lower end slip? If \( \mu\) = 0.75?

Exercise \(\PageIndex{8}\)

It is time for another ladder problem. Most ladders in elementary mechanics problems rest on a rough horizontal floor and lean against a smooth vertical wall. In this problem, both floor and wall are smooth. The ladder starts making an angle of a with the vertical, and then it is released. It immediately starts to slip, of course. After a while it will cease contact with the smooth vertical wall. Show that, at the moment when the upper end of the ladder loses contact with the wall, the angle q that the ladder makes with the vertical is given by \( \cos\theta\ = \frac{2}{3}\cos\alpha\).

Exercise \(\PageIndex{9}\)

If you managed that one all right, this one, which is somewhat similar, should be easy. Maybe.

A uniform solid semicylinder of radius \( a\) and mass \( m\) is placed with its curved surface against a smooth vertical wall and a smooth horizontal floor, its base initially being vertical.

It is then released. Find the reaction \( N_{1}\) of the floor on the semicylinder and the reaction \( N_{2}\) of the wall on the semicylinder when its base makes an angle \( \theta\) with the vertical.

Show that the semicylinder loses contact with the wall when \( \theta\) = 90^o, and that it then continues to rotate until its base makes an angle of 39^o 46' with the vertical before it starts to fall back.

­­­­­­­­­­­­­_________________________

Many problems in elementary mechanics involve a body resting upon or sliding upon an inclined plane. It is time to try a few of these. The first one is very easy, just to get us started. The two following that might be more interesting.

Exercise \(\PageIndex{10}\)

A particle of mass \( m\) is placed on a plane which is inclined to the horizontal at an angle \( \alpha\) that is greater than \( \tan^{-1}\mu\), where \( \mu\) is the coefficient of limiting static friction. What is the least force required to prevent the particle from sliding down the plane?

Exercise \(\PageIndex{11}\)

A cylinder or mass \( m\), radius \( a\), and rotational inertia \( ka^{2}\) rolls without slipping down the rough hypotenuse of a wedge on mass \( M\), the smooth base of which is in contact with a smooth horizontal table. The hypotenuse makes an angle \( \alpha\) with the horizontal, and the gravitational acceleration is \( \text{g}\). Find the linear acceleration of the wedge as it slips along the surface of the table, in terms of \( m,\ M,\ \text{g},\ a,\ k\) and \( \alpha\).

[Note that by saying that the rotational inertia is \( ka^{2}\), I am letting the question apply to a hollow cylinder, or a solid cylinder, or even a hollow or solid sphere.]

Exercise \(\PageIndex{12}\)

A particle is placed on a rough plane inclined at an angle a to the horizontal. It is initially in limiting static equilibrium. It is given an initial velocity \( V_{0}\) along the \( x\)-axis. Ignoring the small difference between the coefficients of moving and limiting static friction, show that at a point on the subsequent trajectory where the tangent to the trajectory makes an angle \( \psi\) with the \( x\)-axis, the speed \( V\) is given by

\( V=\frac{V_{0}}{1+\cos\psi}\)

What is the limiting speed reached by the particle after a long time?

Exercise \(\PageIndex{13}\)

Calculate the moment of inertia of a hollow sphere, mass \( M\), outer radius \( a\), inner radius \( xa\). Express your answer in the form

\( I=\frac{2}{5}Ma^{2}\ \times\ f(x)\).

What does your expression become if \( x=0\)? And if \( x\rightarrow 1\)?

Exercise \(\PageIndex{14}\)

Calculate the moment of inertia of a spherical planet of outer radius \( a\), consisting of a dense core of radius \( xa\) surrounded by a mantle of density \( s\) times the density of the core. Express your answer in the form

\( I=\frac{2}{5}Ma^{2}\times f(x,s)\).

Make sure that, if the density of the core is zero, your expression reduces to the answer you got for Exercise 13.

Draw graphs of \( \frac{I}{(\frac{2}{5}Ma^{2})}\) versus \( x\) (\( x\) going from 0 to 1), for \( s\) = 0.2, 0.4, 0.6 and 0.8.

Show that, for a given mass \( M\) and density ratio \( s\), the moment of inertia is least for a core size give by the solution of

\( 2(I-s)x^{5}+15x^{2}-9=0\)

For a mantle-to-density ratio of 0.6, calculate the core size for which the moment of inertia is least and calculate (in units of \( \frac{2}{5}Ma^{2}\)) the moment of inertia for that core.

Now let’s see if we can determine the core size from a knowledge of the moment of inertia. It is sometimes asserted that one can determine the moment of inertia (and hence the core size) of a planet from the rate of precession of the orbit of a satellite. I am not sure how this would work with a planet such as Mercury, which has never had a satellite in orbit around it. (Mariner 10, while in orbit around the Sun, made three fly-bys past Mercury). Unless a planet departs from spherical symmetry, the orbit of a satellite will not precess, since the gravitational planet is then identical with that from a point mass. And, even if a planet were dynamically oblate, the rate of precession allows us to determine the dynamical ellipticity \( \frac{(C-A)}{C}\), but not either moment of inertia separately.

Nevertheless, let’s suppose that the moment of inertia of a planet is (0.92 ± 1%) % \( \frac{2}{5}Ma^{2}\); specifically, let’s suppose that the moment of inertia has been determined to be between 0.911 and 0.929 % \( \frac{2}{5}Ma^{2}\), and that the mantle-to-core density ratio is known (how?) to be 0.6. Calculate the possible range in the value of the core radius \( x\).

Exercise \(\PageIndex{15}\)

A rectangular brick of length \( 2l\) rests (with the sides of length \( 2l\) vertically) on a rough semicylindrical log of radius \( R\). The drawing below shows three such bricks. In the first one, \( 2l\) is quite short, and it looks is if it is stable. In the second one, \( 2l\) is rather long, and the equilibrium looks decidedly wobbly. In the third one, we’re not quite sure whether the equilibrium is stable or not. What is the longest brick that is stable against small angular displacements from the vertical?

Exercise \(\PageIndex{16}\)

A Thing with a semicylindrical (or hemispherical) base of radius \( a\) is balanced on top of a rough semicylinder (or hemisphere) of radius \( b\) as shown. The distance of the centre of mass of the Thing from the line (or point) of contact is \( l\). Show that the equilibrium is stable if

\( \frac{1}{l}\ >\ \frac{1}{a}+\frac{1}{b}\).

If \( a=b\), is the equilibrium stable if the Thing is

1. A hollow semicylinder?
2. A hollow hemisphere?
3. A uniform solid semicylinder?
4. A uniform solid hemisphere?

Exercise \(\PageIndex{17}\)

A log of square cross-section, sides \( 2a\), rests on two smooth pegs a distance \( 2ka\) apart, one of the diagonals making an angle \( \theta\) with the vertical.

Show that, if \( k\ <\ \frac{1}{\sqrt{8}}\ =\ 0.354\) the only equilibrium position possible is \( \theta\) = 90^o, but that this position is unstable; consequently, following a small displacement, the log will fall out of the pegs. Show that if the pegs are farther apart, with \( 0.354\ <\ k\ <\ 0.500\), three equilibrium positions are possible. Which of them are stable, and which are unstable? If \( k=0.45\), what are the possible equilibrium values of \( \theta\)? Show that, if \( 0.500\ <\ k\ <\ 1.414\), only one equilibrium position is possible, and that it is stable.

Exercise \(\PageIndex{18}\)

A uniform solid hemisphere of radius \( a\) rests in limiting static equilibrium with its curved surface in contact with a smooth vertical wall and a rough horizontal floor (coefficient of limiting static friction \( \mu\)). Show that the base of the hemisphere makes an angle \( \theta\) with the floor, where

\( \sin\ \theta\ =\ \frac{8\mu}{3}\).

Calculate the value of \( \theta\) if (a) \( \mu\ =\ \frac{1}{4}\) and \( \mu\ =\ \frac{3}{8}\).

What happens if \( \mu\ >\ \frac{3}{8}\)?

Exercise \(\PageIndex{19}\)

A uniform rod of length \( 2l\) rocks to and fro on the top of a rough semicircular cylinder of radius \( a\). Calculate the period of small oscillations.

A uniform solid hemisphere of radius \( a\) with its curved surface in contact with a rough horizontal table rocks through a small angle. Show that the period of small oscillations is

\( P\ =\ 2\pi\sqrt{\frac{26a}{15\text{g}}}\).

Exercise \(\PageIndex{21}\)

The density \( \rho\) of a solid sphere of mass \( M\) and radius \( a\) varies with distance \( r\) from the centre as

\( \rho\ =\ \rho_{0}\left(1-\frac{r}{a}\right)\).

Calculate the (second) moment of inertia about an axis through the centre of the sphere. Express your answer in the form of constant % \( Ma^{2}\).

Exercise \(\PageIndex{22}\)

Two identical particles are connected by a light string of length \( 2a\alpha\). The system is draped over a cylinder of radius \( a\) as shown, the coefficient of limiting static friction being \( \mu\). Determine the angle \( \theta\) when the system is in limiting equilibrium and just about to slide.

Exercise \(\PageIndex{23}\)

Una masa\( M\) cuelga de una cuerda ligera que pasa sobre un cilindro rugoso, siendo el coeficiente de fricción\( \mu\) y siendo el ángulo de vuelta\( \alpha\). ¿Cuál es el menor valor de\( F\), la tensión en la parte superior de la cuerda, requerida para evitar que la masa caiga?

Ejercicio\(\PageIndex{24}\)

Un cubo de madera flota sobre el agua. Una de sus caras está articulada libremente a un eje fijado en la superficie del agua. La bisagra se fija a una distancia de la parte superior de la cara igual a\( x\) veces la longitud de un lado. La cara opuesta se sumerge a una distancia\( y\) multiplicada por la longitud de un lado. Encontrar la densidad relativa\( s\) (es decir, relativa a la densidad del agua) de la madera en términos de\( x\) y \( y\).

Ejercicio\(\PageIndex{25}\)

Una esfera sólida uniforme se asienta en la parte superior de un cilindro semicircular rugoso. Se le da un pequeño desplazamiento para que ruede por el costado del cilindro. Demostrar que la parte esférica y cilíndrica compañía cuando la línea que une sus centros hace un ángulo 53 ^o 58' con la vertical.

Ejercicio\(\PageIndex{26}\)

Un alumno tiene un sándwich triangular de lados de 9 cm, 12 cm, 15 cm. Ella toma una mordida semicircular de radio 3 cm fuera de la mitad de la hipotenusa. ¿Dónde está el centro de masa del resto? ¿Está dentro o fuera de la picadura?

Ejercicio\(\PageIndex{27}\)

Una banda elástica de goma es de longitud\( 2\pi a\) y masa\( m\); la constante de fuerza del caucho es\( k\). La banda es lanzada al aire, girando, de manera que toma la forma de un círculo, estirada por la fuerza centrífuga. (Esto requiere mucha práctica, habilidad y destreza manual). Encontrar una relación entre su radio y velocidad angular, en términos de\( a,\ m\) y \( k\).

Ejercicio\(\PageIndex{28}\)

La mayoría de nosotros hemos hecho problemas simples en la fricción en la secundaria o en el primer año en la universidad o universidad. Ya sabes el tipo — un cuerpo yace sobre una mesa horizontal rugosa. Se le aplica una fuerza. ¿Qué pasa? Prueba este.

Encuentra una varilla uniforme AB. Un gobernante lo hará siempre y cuando sea recto y no deformado. O un lápiz de sección transversal hexagonal (no circular), siempre que sea uniforme y no tenga una goma de borrar al final. Colóquelo sobre una mesa horizontal rugosa. Poco a poco aplique una fuerza horizontal perpendicular a la varilla en el extremo A hasta que la varilla comience a moverse. El final A, por supuesto, avanzará. Mira el final B — se mueve hacia atrás. Hay un punto C en algún lugar a lo largo de la varilla que es estacionario. Es decir, el movimiento inicial de la varilla es una rotación alrededor del punto C. Calcular — y medir — la relación AC/AB. ¿Cuál es la fuerza que estás ejerciendo sobre A cuando la varilla está a punto de moverse, en términos de su peso y el coeficiente de fricción?

Ejercicio\(\PageIndex{29}\)

Algunos de los problemas de fricción más temidos son los de “¿Se inclina o se resbala?” tipo. Este y los cuatro siguientes son ejemplos de este tipo.

Un cono circular recto sólido uniforme de altura\( h\) y radio basal\( a\) se coloca sobre un plano inclinado cuya inclinación a la horizontal se incrementa gradualmente. El coeficiente de fricción estática limitante es\( \mu\). ¿Se desliza el cono o se inclina?

Ejercicio\(\PageIndex{30}\)

Un bloque de lado cubico\( 2a\) descansa sobre una mesa horizontal rugosa, siendo el coeficiente de fricción estática limitante\( \mu\). Se aplica una fuerza horizontal que aumenta gradualmente como se muestra a una distancia\( x\) por encima de la tabla. ¿Se deslizará el bloque o se inclinará? Demostrar que, si\( \mu\ < \frac{1}{2}\), el bloque se deslizará cualquiera que sea el valor de\( x\).

Ejercicio\(\PageIndex{31}\)

Un tronco cilíndrico de diámetro\( 2a\) y masa\( m\) descansa sobre dos clavijas rugosas (coeficiente de fricción estática limitante\( \mu\)) a una distancia de\( 2ka\) separación. Se aplica un par\( \tau\) que aumenta gradualmente como se muestra. ¿El tronco se desliza (es decir, gira alrededor de su eje) o se inclina (alrededor de la clavija de la derecha)?

Cuando hayas hecho esa, puedes probar una variante (que no he trabajado y no he publicado una solución) en la que un cilindro de radio\( a\) está descansando contra un bordillo (o bordillo, si prefieres esa ortografía) de altura\( h\), y se aplica un par. ¿Se propina o se resbala?

Ejercicio\(\PageIndex{32}\)

Este problema revela las severas limitaciones de mis habilidades artísticas, pero el dibujo anterior, lo creas o no, representa un automóvil visto desde atrás. Se puede ver al chofer y al pasajero. La altura del centro de masa es\( h\) y la distancia entre las ruedas es\( 2d\). El automóvil se desplaza sobre una superficie de carretera horizontal, coeficiente de fricción\( \mu\), y se dirige hacia la izquierda en un círculo de radio\( R\), estando el centro de curvatura muy alejado a la izquierda del dibujo. A medida que aumenten gradualmente su velocidad, ¿el auto se deslizará hacia la derecha, o se volcará sobre el volante derecho, y a qué velocidad se llevará a cabo este desastre? Afortunadamente, tanto el conductor como el pasajero llevaban el cinturón de seguridad y ninguno de los dos resultó gravemente herido, y nunca más condujeron demasiado rápido a la vuelta de la esquina.

Ejercicio\(\PageIndex{33}\)

Una varilla uniforme de longitud\( 2l\) descansa sobre una mesa, con una longitud\( l-a\) en contacto con la mesa, y el resto,\( l+a\) pegado sobre el borde, es decir,\( a\) es la distancia desde el borde de la mesa hasta la mitad de la varilla. Inicialmente se evita que caiga por una fuerza como se muestra. Cuando se quita la fuerza, la varilla gira alrededor de A. Mostrar que la varilla se desliza cuando hace un ángulo\( \theta\) con la horizontal, donde

\( \tan\ \theta\ =\ \frac{2\mu}{2\ +\ 9(\frac{a}{l})^{2}}\)

Aquí m es el coeficiente de fricción estática limitante en A.

Ejercicio\(\PageIndex{34}\)

Una cadena flexible de masa\( m\) y longitud\( l\) está inicialmente en reposo con una mitad de ella descansando sobre una mesa horizontal lisa, y la otra mitad colgando sobre el borde:

Se libera, para que empiece a deslizarse fuera de la mesa. En un momento posterior\( t\), una longitud\( \frac{1}{2}l-x\) permanece en contacto con la mesa, la longitud restante\( \frac{1}{2}l+x\) colgando verticalmente, y la velocidad de la cadena es\( v\).

Demostrar que

\( v^{2}\ =\ \text{g}x\ +\ \frac{\text{g}}{l}x^{2}\),

\( x\ =\ \frac{l(e^{\sqrt{\frac{\text{g}}{lt}}}-1)^{2}}{4e^{\sqrt{\frac{\text{g}}{lt}}}}\)

\( v\ =\ \frac{\sqrt{\text{g}l}(e^{\sqrt{\frac{\text{4g}}{lt}}}-1)}{4e^{\sqrt{\frac{\text{4g}}{lt}}}}\)

Ejercicio\(\PageIndex{35a}\)

Cuatro libros, cada uno de ancho\( 2w\), se apilan uno encima del otro en un montón, así:

¿Cuál es el voladizo máximo posible,\( D\)?

Ejercicio\(\PageIndex{35b}\)

¿Cuántos libros se necesitarían para lograr un voladizo de\( 10w\)?

Ejercicio\(\PageIndex{35c}\)

Dado un suministro ilimitado de libros, ¿cuál es el voladizo máximo alcanzable?

Ejercicio\(\PageIndex{36}\)

El Hombre y el Perro.

En su momento\(t = 0\), el Hombre se encuentra en el origen de las coordenadas, y comienza a caminar por el\(y\) eje a velocidad constante\(v\). El Perro comienza en\((a , 0) \) y corre a velocidad constante\(Av (v > 1)\) hacia el Hombre. La velocidad del Perro siempre se dirige directamente hacia el Hombre. Encuentra una ecuación para el camino perseguido por el Perro, y dibuja una gráfica de este camino. ¿Hasta dónde ha caminado el Hombre cuando el Perro llega al Hombre, y cuánto tiempo lleva esto?

Ejercicio\(\PageIndex{37}\)

Una partícula A de masa\(m\) está unida por una cuerda ligera a una segunda partícula, B, también de masa\(m\). A descansa sobre una mesa horizontal lisa, mientras que B cuelga verticalmente a través de un agujero en la mesa. En el tiempo cero, la longitud de la porción horizontal de la cuerda (es decir, la distancia de A desde el agujero) es a, y A se mueve sobre la mesa en un círculo horizontal de radio a con velocidad angular inicial\( \omega_0\).

En algún momento posterior la longitud de la porción horizontal de la cuerda es\(r\) y la velocidad angular de A es\( \omega \). Denotemos por la tasa de incremento de\(r\) con el tiempo, lo que evidentemente será negativo si B está cayendo.

Ejercicio\(\PageIndex{37a }\)

Demostrar que\( \dot{r} \) se da por

\[ \frac{\dot{r}^2}{ga} = 1 + \frac{a \omega^2_0}{2g} \left( 1- \frac{\omega}{\omega_0}\right) - \sqrt{\frac{\omega}{\omega_0}}. \label{eq:1} \]

Ejercicio\(\PageIndex{37b}\)

Demostrar eso, si\(a \omega^2_0 = g \), donde\( \Omega = \omega \ \omega_0 \).

\[ \frac{ \dot{r}^2}{ga} = \frac{3}{2} - \frac{1}{2} \Omega - 1 / \sqrt{\Omega} , \label{eq:2} \]

Ejercicio\(\PageIndex{37c}\)

Demostrar que sólo hay un valor de Ω, a saber, 1, para lo cual existe una solución real para\( \dot{r} \), a saber\( \dot{r} = 0 \). Esto implica que el sistema permanece en equilibrio, con el radio del círculo, la velocidad angular de A y la altura de B permaneciendo constantes, permaneciendo la fuerza centrífuga sobre A igual al peso de B.

Ejercicio\(\PageIndex{37d }\)

Demostrar que si\( a \omega^2_0 = 2g \),

\( \frac{\dot{r}^2}{ga} = 2 - \Omega - 1 / \sqrt{ \Omega} \)

y que A se mueve hacia afuera (su velocidad angular decreciente) y B se mueve hacia arriba,

alcanzando una velocidad máxima de\( \dot{r} = 0.331841 \sqrt{ga} \)

donde\( \dot{r} = 1.259921 a \)

cuando\( \omega = 0.629961 \omega_0, \)

y alcanza un equilibrio cuando\( \dot{r} = 0 \)

donde\( \dot{r} = 1.618034a \)

cuando\( \omega = 0.381966 \omega_0. \)

Ejercicio\(\PageIndex{37e}\)

Demostrar que si\( a \omega^2_0 = \frac{1}{2}g\),

\( \frac{ \dot{r}^2}{ga} = \frac{5}{4} - \frac{1}{4} \Omega - 1 / \sqrt{ \Omega} ,\)

y que A se mueve hacia adentro (aumenta su velocidad angular) y B se mueve hacia abajo,

alcanzando una velocidad máxima de\( \dot{r} = -0.243822 \sqrt{ga} \)

donde\( r = 0.793701 a \)

cuando\( \omega = 1.587401 \omega_0, \)

y alcanza un equilibrio cuando\( \dot{r} = 0\)

donde\( r = 0.640338a\)

cuando\( \omega = 2.438447 \omega_0. \)

Ejercicio\(\PageIndex{38}\)

Este problema —el péndulo de torsión bifilar— me lo sugirió Claude Plathey, quien utilizó el método en una aplicación práctica para determinar la inercia rotacional (momento de inercia) de una varilla real no uniforme. También me llamó la atención sobre un interesante trabajo sobre la determinación de los momentos de inercia de los cuerpos (¡como los aviones!) por el método: naca.larc.nasa.gov/digidoc/re... ACA-TR-467.PDF

Una varilla simétrica pero no necesariamente uniforme de masa\(m\) y momento de inercia\(I\) se suspende del techo por dos hilos ligeros cada uno de longitud a\(L\) una\(D\)\( (D << L )\) distancia.La varilla se tuerce alrededor de un eje vertical a través de su punto medio a través de un ángulo pequeño y luego liberado. Encuentra el periodo de pequeñas oscilaciones en el plano horizontal.

Ejercicio\(\PageIndex{39}\)

Un yoyo es de masa M e inercia rotacional\(I\). El radio de su eje es\(a\), y cae de la manera habitual con una longitud de cuerda envuelta alrededor del eje.

Cómo es que su aceleración lineal hacia abajo es

\( \frac{Ma^2}{Ma^2 + I} \times g \)

y que la tensión en la cuerda i

\(\frac{I}{Ma^2+ 1} \times Mg \)

Ejercicio\(\PageIndex{40a }\)

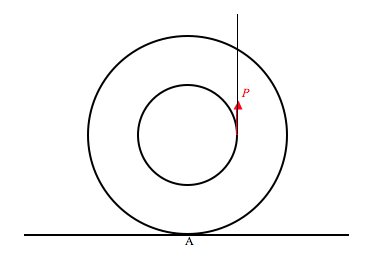
Un yoyo, masa\(M\), radio del eje\(a\), radio exterior\(b\), descansa sobre una mesa horizontal como se muestra. La cuerda, enrollada alrededor del eje, se sujeta verticalmente como se muestra, y\(P\) se aplica una fuerza. El coeficiente de fricción entre yoyo y mesa es\( \mu \). Demostrar que, si

\( \mu > \frac{MabP}{(Mg-P)(I + Mb^2}, \)

el movimiento inicial del yoyo será rodar hacia la izquierda sin deslizarse, con una aceleración lineal inicial

\( \frac{abP}{I + Mab} ; \)

pero que si

\( \mu < \frac{MabP}{(Mg-P)(I + Mb^2}, \)

el yoyo girará en sentido contrario a las agujas del reloj sin rodar, con una aceleración angular inicial de aproximadamente C de

\( \frac{P(a - \mu) - \mu Mg }{I}. \)

Ejercicio\(\PageIndex{40b}\)

Un yoyo, masa\( M\), radio del eje\( a\), radio exterior\( b\), descansa sobre una mesa horizontal como se muestra. La cuerda, enrollada alrededor del eje, se sujeta horizontalmente como se muestra, y\( P\) se aplica una fuerza. El coeficiente de fricción entre yoyo y mesa es\( \mu\).

i) Demostrar que, si\( I>Mab\):

Si

\( \mu\ >\ \left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\)

el movimiento inicial del yoyo será rodar hacia la derecha sin deslizarse, con una aceleración lineal inicial

\( \frac{Pb(a+b)}{I+Mb^{2}}\);

pero eso, si

\( \mu\ <\ \left(\frac{I-Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\),

el yoyo acelera simultáneamente hacia la derecha con una aceleración lineal de

\( \frac{P-\mu M\text{g}}{M}\)

mientras experimenta una aceleración angular en sentido horario alrededor de C de

\( \frac{Pa\ +\ \mu M\text{g}b}{I}\).

ii) Demostrar que, si\( I>Mab\):

Si

\( \mu\ >\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)\),

el movimiento inicial del yoyo será rodar hacia la derecha sin deslizarse, con una aceleración lineal inicial

\( \frac{Pb(a+b)}{I+Mb^{2}}\);

pero eso, si

\( \mu\ <\ \left(\frac{Mab-I}{Mb^{2}+I}\right)\left(\frac{P}{M\text{g}}\right)\),

el yoyo acelera simultáneamente hacia la derecha con una aceleración lineal de

\( \frac{P\ +\ \mu M\text{g}}{M}\)

mientras experimenta una aceleración angular en sentido horario alrededor de C de

\( \frac{Pa\ -\ \mu M\text{g}b}{I}\).

iii) Demostrar que, si\( I>Mab\):

Ejercicio\(\PageIndex{40c}\)

(Después del Problema 40 b) este es mucho más fácil y un alivio bienvenido.)

Un yo-yo, masa\( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held horizontally as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is m.

Show that, if

\( \mu\ >\ \left(\frac{I+Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\),

the initial motion of the yo-yo will be to roll to the right without slipping, with an initial linear acceleration

\( \frac{Pb(b-a)}{I+Mb^{2}}\)

and angular acceleration

\( \frac{P(b-a)}{I+Mb^{2}}\)

but that, if

\( \mu\ <\ \left(\frac{I+Mab}{I+Mb^{2}}\right)\left(\frac{P}{M\text{g}}\right)\)

the yo-yo slips at A. C accelerates to the right at a rate of \( \frac{P-\mu M\text{g}}{M}\), while the yo-yo spins around C with a counterclockwise angular acceleration of \( \frac{Pa-\mu M\text{g}b}{I}\).

Exercise \(\PageIndex{40d}\)

A yo-yo, mass \( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held at an angle \( \theta\) to the horizontal as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is \( \mu\).

The complete analysis of this problem is similar to that of Problem 40(b), except that a factor of \( \cos\theta\) appears in many of the equations. No new phenomena appear, and the analysis is tedious without any new points of interest. For that reason I limit this problem to asking you to show that the direction of the frictional force of the table on the yo-yo at A depends upon whether the \( \cos\theta\) is less than or greater than \( \frac{Mab}{I}\).

Exercise \(\PageIndex{40e}\)

A yo-yo, mass \( M\), axle radius \( a\), outer radius \( b\), rests on a horizontal table as shown. The string, wrapped around the axle, is held at an angle \( \theta\) to the horizontal as shown, and a force \( P\) is applied. The coefficient of friction between yo-yo and table is \( \mu\).

Show that, provided there is no slipping, the yo-yo rolls to the right if \( \cos\theta>\frac{a}{b}\) and to the left if \( \cos\theta<\frac{a}{b}\). Describe what happens if \( \cos\theta=\frac{a}{b}\).

Exercise \(\PageIndex{41}\)

A uniform plane lamina of mass \( 3m\) is in the form of a truncated square like the one above.

Find the position of the centre of mass, the principal moments of inertia with respect to the centre of mass, and the eccentricity and inclination of the momental ellipse.

Exercise \(\PageIndex{42}\)

A mass \( M\) sits on a smooth horizontal table. A second mass, \( m\), hangs from the first by a light inextensible string. A slot in the table allows \( m\) and the string to swing as a pendulum.

The system is then set in motion with the pendulum swinging, and the mass \( M\) sliding back and forth on the table. At some instant when the horizontal displacement of \( M\) from its equilibrium position is \( x\) the string makes an angle \( \theta\) with the vertical.

Show that the equations of motion are

\( (M+m)\ddot{x}\ +\ ml(\ddot{\theta}\cos\theta\ -\ \dot{\theta}^{2}\sin\theta)\ =\ 0\),

\( I\ddot{\theta}\ +\ \ddot{x}\cos\theta\ -\ \dot{x}\sin\theta\dot{\theta}\ =\ -\text{g}\sin\theta\).

Show that for small oscillations \( (\cos\theta\approx 1,\ \sin\theta\approx\theta,\ \dot{\theta}^{2}\theta<<\ddot{\theta},\ \dot{x}\theta\dot{\theta}<<\text{g})\) the period the motion is approximately \( 2\pi\sqrt{\frac{Ml}{(M+m)\text{g}}}\). Note that, if \( m<<M\), this reduces to \( 2\pi\sqrt{\frac{l}{\text{g}}}\) as expected.

Exercise \(\PageIndex{43}\)

A gun projects a shell, in the absence of air resistance, at an initial angle to the horizontal. The speed of projection varies with the angle \( \alpha\) of projection and is given by

initial speed = \( V_{0}\cos\frac{1}{2}\alpha\).

Show that, in order to achieve the greatest range on the horizontal plane, the shell should be projected at an angle to the horizontal whose cosine \( c\) is given by the solution of the equation

\( 3c^{3}+2c^{2}-2c-1=0\)

and determine this angle to the nearest arcminute.

Exercise \(\PageIndex{44}\)

The length of a cylindrical log is \( L\) times its diameter, and its density is \( s\) times that of water \( (0<s<1)\). Show that the log can float vertically in stable equilibrium, whatever its density, provided that \( L<0.707\). and that, if its length is greater than this, it can float vertically in stable equilibrium only if

\( L<\frac{1}{\sqrt{8s(1-s)}}\).

Show that, if the length is equal to the diameter, it can float in stable equilibrium with its cylindrical axis vertical only if its density is less than 0.146 or greater than 0.854 times that of water.

Exercise \(\PageIndex{45}\)

A uniform heavy rod of length 6 hangs from a fixed point C by means of two light strings of lengths 4 and 5. What angle does the rod make with the horizontal?

Incidentally, a (4, 5, 6) triangle has the interesting property that one of its angles is exactly twice one of the other ones.

Exercise \(\PageIndex{46}\)

A uniform rod rests on two smooth (frictionless) planes inclined at 30º and 45º to the horizontal. What angle does the rod make with the horizontal?

Exercise \(\PageIndex{47}\)

A uniform rod of length \( 2l\) rests on the inside of a circular cylindrical pipe of radius \( a\). The coefficient of limiting static friction (often known for short, if with less precision, as “the”coefficient of friction) \( \mu\). What is the maximum angle \( \theta\) that the rod can make with the horizontal in static equilibrium?