3: Fotos de Schrödinger y Heisenberg
- Page ID
- 131526
Hasta ahora hemos asumido que los estados cuánticos que\(|\psi(t)\rangle\) describen el sistema llevan la dependencia del tiempo. Sin embargo, esta no es la única manera de hacer un seguimiento de la evolución del tiempo. Dado que todas las cantidades físicamente observadas son valores de expectativa, podemos escribir
\ [\ begin {alineado}
\ langle A\ rangle &=\ nombreoperador {Tr} [|\ psi (t)\ rangle\ langle\ psi (t) | A] =\ nombreoperador {Tr}\ izquierda [U (t) |\ psi (0)\ rangle\ langle\ psi (0) | U^ {\ daga} (t) A\ derecha]\
=\ nombreoperador {Tr}\ izquierda [|\ psi (0)\ rangle\ langle\ psi (0) | U^ {\ daga} (t) A U (t)\ derecha]\ quad\ text {( propiedad cíclica)}\\
&\ equiv\ nombreoperador {Tr} [|\ psi (0)\ rangle\ langle\ psi (0) | A (t)],
\ end {alineado}\ tag {3.1}\]
donde definimos el operador variable en el tiempo\(A(t)=U^{\dagger}(t) A U(t)\). Claramente, ¡podemos hacer un seguimiento de la evolución del tiempo en los operadores!
- Schrödinger picture: Lleve un registro de la evolución del tiempo en los estados,
- Imagen de Heisenberg: Lleve un registro de la evolución del tiempo en los operadores.
Podemos etiquetar los estados y operadores “\(S\)” y “\(H\)” dependiendo de la imagen. Por ejemplo,
\[\left|\psi_{H}\right\rangle=\left|\psi_{S}(0)\right\rangle \quad \text { and } \quad A_{H}(t)=U^{\dagger}(t) A_{S} U(t)\tag{3.2}\]
La evolución temporal para los estados viene dada por la ecuación de Schrödinger, por lo que queremos una “ecuación de Heisenberg” correspondiente para los operadores. Primero, observamos que
\[U(t)=\exp \left(-\frac{i}{\hbar} H t\right),\tag{3.3}\]
de tal manera que
\[\frac{d}{d t} U(t)=-\frac{i}{\hbar} H U(t)\tag{3.4}\]
A continuación, calculamos la derivada de tiempo de\(\langle A\rangle\):
\[\frac{d}{d t} \operatorname{Tr}\left[\left|\psi_{S}(t)\right\rangle\left\langle\psi_{S}(t)\right| A_{S}\right]=\frac{d}{d t}\left\langle\psi_{S}(t)\left|A_{S}\right| \psi_{S}(t)\right\rangle=\frac{d}{d t}\left\langle\psi_{H}\left|A_{H}(t)\right| \psi_{H}\right\rangle\tag{3.5}\]
La última ecuación se desprende de la Ec. (3.1). Ahora podemos calcular
\ [\ begin {alineado}
\ frac {d} {d t}\ izquierda\ langle\ psi_ {S} (t)\ izquierda|A_ {S}\ derecha|\ psi_ {S} (t)\ derecha\ rangle &=\ frac {d} {d t}\ izquierda\ langle\ psi_ {S} (0)\ izquierda|u^ {\ daga} (t) A_ {S} U (t)\ derecha|\ psi_ {S} (0)\ derecha\ rangle\\
&=\ izquierda\ langle\ psi_ {S} (0)\ izquierda|\ izquierda [\ punto {U} ^ {\ daga} (t) A_ {S} U (t) +U^ {\ daga} (t)\ punto {A} _ {S} U (t) +U^ {\ daga} (t) A_ {S}\ punto {U} (t)\ derecha]\ derecha|\ psi_ {S} (0)\ derecha\ rangle\\
&=\ izquierda\ langle\ psi_ {H}\ izquierda|\ izquierda [\ frac {i} {\ hbar} H A_ {H} (t) -\ frac {i} {\ hbar} A_ {H} (t) H+\ frac {\ parcial A_ {H} (t)} {\ parcial t}\ derecha]\ derecha|\ psi_ {H}\ derecha\ rangle\\
&=-\ frac {i } {\ hbar}\ izquierda\ langle\ psi_ {H}\ izquierda|\ izquierda [A_ {H} (t), H\ derecha]\ derecha|\ psi_ {H}\ derecha\ rangle+\ izquierda\ langle\ psi_ {H}\ izquierda|\ frac {\ parcial A_ {H} (t)} {\ parcial t}\ derecha|\ psi_ {H}\ derecha\ rangle\\
&=\ izquierda\ langle\ psi_ {H}\ izquierda|\ frac {d A_ {H} (t)} {d t}\ derecha|\ psi_ {H}\ derecha\ rangle
\ final {alineado}\ tag {3.6}\]
Dado que esto debe ser cierto para todos\(\left|\psi_{H}\right\rangle\), esta es una identidad de operador:
\[\frac{d A_{H}(t)}{d t}=-\frac{i}{\hbar}\left[A_{H}(t), H\right]+\frac{\partial A_{H}(t)}{\partial t}\tag{3.7}\]
Esta es la ecuación de Heisenberg. Observe la diferencia entre la “recta\(d\)” y la “rizada\(\partial\)” en la derivada de tiempo y la derivada de tiempo parcial, respectivamente. La derivada parcial se ocupa únicamente de la dependencia explícita del tiempo del operador. En muchos casos (como la posición y el impulso) esto es cero.
Hemos visto que tanto la ecuación de Schrödinger como la de Heisenberg se desprende del formalismo espacial Hilbert de mecánica cuántica de Von Neumann. En consecuencia, hemos demostrado que este formalismo unifica adecuadamente tanto la mecánica de las olas de Schrödingers como la mecánica matricial de Heisenberg, Born y Jordans.
A modo de ejemplo, consideremos un qubit con evolución temporal determinada por el hamiltoniano\(H=\frac{1}{2} \hbar \omega Z\), con\(Z=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)\). Esto puede ser un giro en un campo magnético, por ejemplo, tal que\(\omega=-e B / m c\). Queremos calcular la evolución temporal del operador\(X_{H}(t)\). Ya que trabajamos solo en el cuadro de Heisenberg, omitiremos el subíndice\(H\). Primero, evaluamos el conmutador en la ecuación de Heisenberg
\[i \hbar \frac{1}{2} \frac{d X}{d t}=\frac{1}{2}[X, H]=-i \hbar \frac{\omega}{2}Y,\tag{3.8}\]
donde definimos\(Y=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right)\). Entonces ahora debemos conocer también la evolución temporal\(Y\) de:
\[i \hbar \frac{1}{2} \frac{d Y}{d t}=\frac{1}{2}[Y, H]=i \hbar \frac{\omega}{2} X\tag{3.9}\]
Estas son dos ecuaciones lineales acopladas, que son relativamente fáciles de resolver:
\[\dot{X}=-\omega Y \quad \text { and } \quad \dot{Y}=\omega X \quad \text { and } \quad \dot{Z}=0\tag{3.10}\]
Podemos definir dos nuevos operadores\(S_{\pm}=X \pm i Y\), y obtener
\[\dot{S}_{\pm}=-\omega Y \pm i \omega X=\pm i \omega S_{\pm}.\tag{3.11}\]
Resolver estas dos ecuaciones rinde\(S_{\pm}(t)=S_{\pm}(0) e^{\pm i \omega t}\), y esto lleva a
\ [\ begin {alineado}
X (t) &=\ frac {S_ {+} (t) +S_ {-} (t)} {2} =\ frac {S_ {+} (0) e^ {i\ omega t} +S_ {-} (0) e^ {-i\ omega t}} {2}\
&=\ frac {1} {2} izquierda [X (0) e^ {i\ omega t} +i Y (0) e^ {i\ omega t} +X (0) e^ {-i\ omega t} -i Y (0) e^ {-i\ omega t}\ derecha]\\
&=X (0)\ cos (\ omega t) -Y (0) \ sin (\ omega t).
\ end {alineado}\ tag {3.12}\]
Se le pide que lo demuestre\(Y(t)=Y(0) \cos (\omega t)+X(0) \sin (\omega t)\) en el ejercicio 3.
Ahora tomamos\(\left|\psi_{H}\right\rangle=|0\rangle\) y\(X(0)=\left(\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right)\),\(Y(0)=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right)\). El valor de expectativa de entonces\(X(t)\) se calcula fácilmente para ser
\[\langle 0|X(t)| 0\rangle=\cos (\omega t)\langle 0|X(0)| 0\rangle-\sin (\omega t)\langle 0|Y(0)| 0\rangle=0\tag{3.13}\]
Alternativamente, cuando\(\left|\psi_{H}\right\rangle=|\pm\rangle\), encontramos
\[\langle+|X(t)|+\rangle=\cos (\omega t) \quad \text { and } \quad\langle+|Y(t)|+\rangle=\sin (\omega t)\tag{3.14}\]
Este es un movimiento circular en el tiempo:
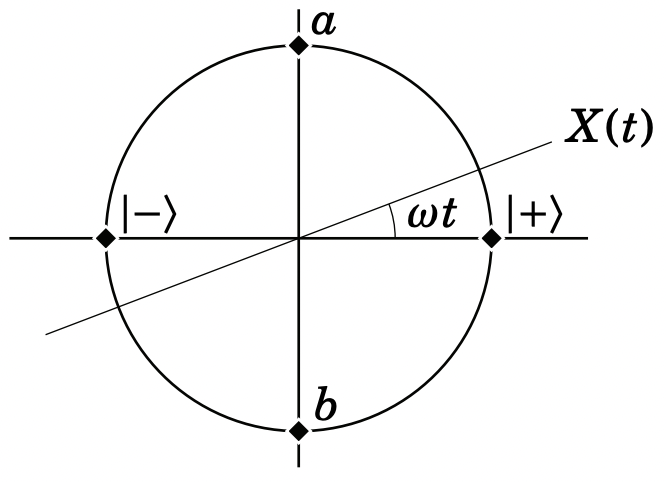
El eigenstate de\(X(\pi / 2)\) es punto\(a\), y el eigenstate de\(X(-\pi / 2)\) es punto\(b\). Además,\(X(\pm \pi / 2)=\mp Y(0)\), y los estados en el punto\(a\) y por lo tanto\(b\) son los autoestados de\(Y\):
\[\left|\psi_{a}\right\rangle=\frac{|0\rangle-i|1\rangle}{\sqrt{2}} \quad \text { and } \quad\left|\psi_{b}\right\rangle=\frac{|0\rangle+i|1\rangle}{\sqrt{2}}\tag{3.15}\]
Una pregunta natural para hacer es dónde\(|1\rangle\) encajan los estados\(|0\rangle\) y en esta imagen. Estos son los autoestados del operador\(Z\), que utilizamos para generar la evolución unitaria del tiempo. Claramente los estados en el círculo nunca llegan a ser ninguno\(|0\rangle\) o\(|1\rangle\), por lo que necesitamos agregar otra dimensión:
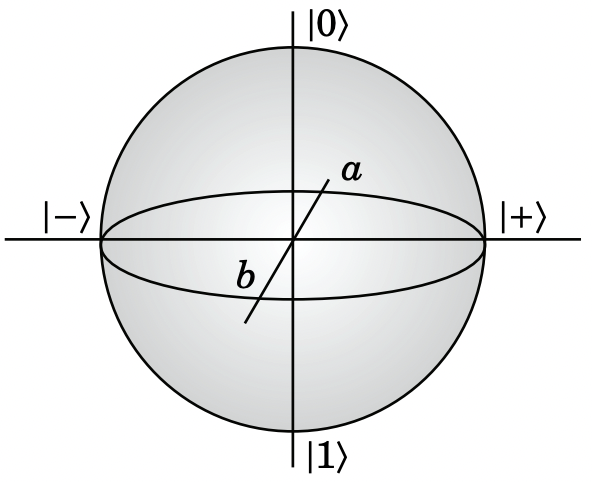
Esto se llama la esfera Bloch, y los operadores están representados por líneas rectas a través del origen. El eje de rotación para las líneas rectas que giran con el tiempo está determinado por el hamiltoniano. En el caso anterior el hamiltoniano era proporcional a\(Z\), lo que significa que las líneas rectas giran alrededor del eje a través de los propios de\(Z\), que son\(|0\rangle\) y\(|1\rangle\).
- Demuéstralo para el hamiltoniano\(H_{S}=H_{H}\).
- El oscilador armónico tiene la ecuación de valor propio de energía\(H|n\rangle=\hbar \omega\left(n+\frac{1}{2}\right)|n\rangle\).
- La solución clásica del oscilador armónico viene dada por
\[|\alpha\rangle=e^{-\frac{1}{2}|\alpha|^{2}} \sum_{n=0}^{\infty} \frac{\alpha^{n}}{\sqrt{n !}}|n\rangle,\tag{3.16}\]
en el límite de\(|\alpha| \gg 1\). Demostrar que\(|\alpha\rangle\) es un estado normalizado correctamente para cualquier\(\alpha \in \mathbb{C}\).
- Calcular el estado de evolución en el tiempo\(|\alpha(t)\rangle\).
- Presentamos los operadores de escalera\(\hat{a}|n\rangle=\sqrt{n}|n-1\rangle\) y\(\hat{a}^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle\). Mostrar que el operador numérico definido por\(\hat{n}|n\rangle=n|n\rangle\) puede escribirse como\(\hat{n}=\hat{a}^{\dagger} \hat{a}\).
- Escribir el estado coherente\(|\alpha\rangle\) como una superposición de operadores de escalera que actúan sobre el estado base\(|0\rangle\).
- Tenga en cuenta que el estado fundamental es independiente del tiempo\((U(t)|0\rangle=|0\rangle)\). Calcular la evolución temporal de los operadores de escalera.
- Calcular la posición\(\hat{q}=\left(\hat{a}+\hat{a}^{\dagger}\right) / 2\) y el momento\(\hat{p}=-i\left(\hat{a}-\hat{a}^{\dagger}\right) / 2\) del oscilador armónico en la imagen de Heisenberg. ¿Se puede identificar el movimiento armónico clásico?
- La solución clásica del oscilador armónico viene dada por
- Dejar\(A\) ser un operador dado por\(A=a_{0}\mathbb{I}+a_{x} X+a_{y} Y+a_{z} Z\). Calcular la matriz\(A(t)\) dada la hamiltoniana\(H=\frac{1}{2} \hbar \omega Z\), y mostrar que\(A\) es hermitiana cuando las\(a_{\mu}\) son reales.
- El cuadro de interacción.
- Que el hamiltoniano de un sistema sea dado por\(H=H_{0}+V\), con\(H_{0}=p^{2} / 2 m\). Usando\(|\psi(t)\rangle_{I}=U_{0}^{\dagger}(t)|\psi(t)\rangle_{S}\) con\(U_{0}(t)=\exp \left(-i H_{0} t / \hbar\right)\), calcula la dependencia del tiempo de un operador en la imagen de interacción\(A_{I}(t)\).
- Definir\(H_{I}(t)=U_{0}^{\dagger}(t) V U_{0}(t)\), mostrar que
\[i \hbar \frac{d}{d t}|\psi(t)\rangle_{I}=H_{I}(t)|\psi(t)\rangle_{I}\tag{3.17}\]
¿Es\(H_{I}\) idéntico a\(H_{H}\) y\(H_{S}\)?
- El operador del tiempo en mecánica cuántica.
- Dejar\(H|\psi\rangle=E|\psi\rangle\), y asumir la existencia de un operador de tiempo conjugado con\(H\), es decir,\([H, T]=i \hbar\). Demostrar que
\[H e^{i \omega T}|\psi\rangle=(E-\hbar \omega) e^{i \omega T}|\psi\rangle\tag{3.18}\]
- Dado eso\(\omega \in \mathbb{R}\), calcular el espectro de\(H\).
- La energía de un sistema debe estar delimitada desde abajo para evitar la decadencia infinita a estados energéticos cada vez más bajos. ¿Para qué significa esto\(T\)?
- Dejar\(H|\psi\rangle=E|\psi\rangle\), y asumir la existencia de un operador de tiempo conjugado con\(H\), es decir,\([H, T]=i \hbar\). Demostrar que
- Considera un átomo de tres niveles con dos estados bajos (degenerados)\(|0\rangle\) y\(|1\rangle\) con energía cero, y un nivel alto\(|e\rangle\) (el estado “excitado”) con energía\(\hbar \omega\). Los niveles bajos se acoplan al nivel excitado por campos ópticos\(\Omega_{0} \cos \omega_{0} t\) y\(\Omega_{1} \cos \omega_{1} t\), respectivamente.
- Dar el hamiltoniano (dependiente del tiempo)\(H\) para el sistema.
- La dependencia del tiempo en\(H\) es difícil de tratar, por lo que debemos transformarnos al marco giratorio a través de alguna transformación unitaria\(U(t)\). Demostrar que
\(H^{\prime}=U(t) H U^{\dagger}(t)-i \hbar U \frac{d U^{\dagger}}{d t}\)
Se puede utilizar la ecuación de Schrödinger con\(|\psi\rangle=U^{\dagger}\left|\psi^{\prime}\right\rangle\).
- Calcular\(H^{\prime}\) si\(U(t)\) es dado por
\ (U (t) =\ left (\ begin {array} {ccc}
1 & 0 & 0\\
0 & e^ {-i\ left (\ omega_ {0} -\ omega_ {1}\ derecha) t} & 0\\
0 & 0 & e^ {-i\ omega_ {0} t}
\ end {array}\ derecha)\)¿Por qué podemos ignorar la dependencia del tiempo restante en\(H^{\prime}\)? Esto se llama Aproximación de Ondas Rotativas.
- Calcular\(\lambda=0\) el estado propio de\(H^{\prime}\) en el caso donde\(\omega_{0}=\omega_{1}\).
- Diseñar una manera de llevar el átomo del estado\(|0\rangle\) a\(|1\rangle\) sin poblar nunca el estado\(|e\rangle\).