14.1: Despertar en barco

Combinar nuestro análisis de la relación de dispersión del agua y la discusión de la sección 11.5 y de la velocidad de grupo en la sección 10.2.1 nos permitirá dar una interpretación simple de uno de los fenómenos de onda más bellos y sutiles de todos: la estela Kelvin.

Despierta

El tema general de las vigilias es muy complicado. Sin embargo, en el caso más simple de movimiento con velocidad constante, la simetría del sistema permite hacer un análisis lineal bastante simple. Esto nos permitirá comprender algunas de las características más obvias de la estela de una manera sencilla, incluyendo el ángulo y las ondas regulares que aparecen a lo largo de la estela, apareciendo al atardecer como perlas en una cuerda, como en la Figura\( 14.2\). ² Si bien no creo que haya mucho que sea original en el tratamiento aquí, el enfoque es un poco inusual,

Figura\( 14.1\): Despierta en el mar. ¹ (Dominio público; Christian Ekelund US Navy)

Figura 14.2: Un velorio al atardecer.

© Fuente desconocida. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte https://ocw.mit.edu/help/faq-fair-use.

como el enfoque de la difracción en el capítulo 13), y creo que da una inclinación útil no sólo en la estela, sino también en el concepto crucial de velocidad de grupo.

Análisis lineal de la estela Kelvin

Considera un océano infinito en el\(x\)\(y\) avión con un bote (pato, lo que sea) moviéndose\(v > 0\) a velocidad constante a lo largo del\(x\) eje. El camino de la embarcación divide la superficie del océano en dos regiones, relacionadas entre sí por la reflexión en el camino. Por lo tanto, podemos sin pérdida de generalidad enfocarnos en el medio plano\(y > 0\). No vamos a tratar de describir en detalle lo que sucede cerca de la\(y = 0\) línea. En muchas situaciones, esto implica turbulencia, y está mucho más allá del alcance de un curso de olas iniciales. Pero lejos de\(y = 0\), es posible aplicar un análisis lineal, y pensar en las ondas\(y > 0\) como combinaciones lineales de ondas planas con condiciones de límite adecuadas a lo largo de la\(y = 0\) línea. ³ Supondremos que lo que pase cerca\(y = 0\) produce una desurbancia localizada en el\(y\) eje que se mueve junto con la embarcación. Esto es necesariamente un paquete de ondas que involucra un rango de frecuencias. La integración sobre todas estas frecuencias da lugar a la estela. Ese es el plan. Haremos esto para algunas condiciones límite ilustrativas simples, y argumentaremos que se puede entender mucho sobre el sistema que es independiente de los detalles de la condición límite. La idea es aprovechar el hecho de que la perturbación es un paquete de ondas, y entender el análogo apropiado en esta situación bidimensional de la velocidad del grupo por la que se mueven los paquetes de ondas.

Este sistema es invariante bajo traducciones simultáneas en el espacio y el tiempo. \[t \rightarrow t+\tau \quad x \rightarrow x+v \tau\]

Estamos buscando una solución en estado estacionario en la que lo único que sucede son las olas inducidas por el movimiento de la embarcación. Esta solución debe depender solo de la combinación\[x-v t\]

y ser invariantes bajo (14.1). Esto significa que la ola estela está estacionaria en un marco de referencia que se mueve junto con la embarcación.

Una manera equivalente (y quizás más física) de decir esto es que la solución que describe solo las olas producidas por la embarcación en movimiento es una combinación lineal de ondas planas que se mueven junto con la embarcación en la\(x\) dirección, es decir, tienen\(k_{x}=\omega / v\).

De cualquier manera, la solución general parece\[\int d \omega f(\omega) e^{-i\left[\omega(t-x / v)-k_{y} y\right]}\]

La función\(f(\omega)\) describe el paquete de ondas en frecuencia, y se determina por el desplazamiento del paquete de ondas en\(y = 0\) y\(t = 0\), a través de la transformada de Fourier\[\psi(x)=\int d \omega f(\omega) e^{i \omega x / v} \Rightarrow f(\omega)=\frac{1}{2 \pi} \int d \tau \psi(v \tau) e^{-i \omega \tau}\]

La relación entre\(\omega\) y\[k=\sqrt{k_{x}^{2}+k_{y}^{2}}\]

viene dada por la relación de dispersión para las olas de agua. Resultará que suele ser una buena aproximación para ignorar la tensión superficial, por lo que se utilizará una aproximación simple en la que la relación de dispersión depende únicamente de la gravedad. También asumiremos que el agua es profunda. Entonces la relación de dispersión es simplemente\[\omega^{2}=g k\]

La magnitud de la velocidad de fase es así\[v_{\phi}=\frac{\omega}{k}=\frac{g}{\omega}\]

Tenga en cuenta que el coeficiente del lado derecho en la dispersión depende de los detalles de la física, pero la estructura general de la relación se deriva simplemente del análisis dimensional. La única combinación de\(g\) y\(k\) con unidades de\(\omega^{2}\) es\(g\)\(k\).

Para (14.3), tenemos\[k=\left(k_{x}^{2}+k_{y}^{2}\right)^{1 / 2}\]

con\[k_{x}=\omega / v\]

Así\ [\ comenzar {reunido}
\ omega^ {4} =g^ {2}\ izquierda (\ omega^ {2}/v^ {2} +k_ {y} ^ {2}\ derecha)\\
k_ {y} =\ izquierda (\ omega^ {4}/g^ {2} -\ omega^ {2}/v^ {2}\ derecha)/2}
\ fin {reunidos}\]

donde el signo de la raíz cuadrada está determinado por la condición de límite en\(y = +\infty\). Si\(k_{y}\) es real,\(k_{y} / \omega\) es un número positivo para que las ondas de fase en (14.3) se propaguen desde la\(y = 0\) línea. Si\(k_{y}\) es imaginario, es i veces un número positivo, de modo que la amplitud se desvanezca como\(y \rightarrow+\infty\) para\(y > 0\). Estos signos son opuestos para\(y < 0\), pero nada más en el análisis cambia, por lo que la solución es simétrica sobre\(y = 0\), como debe ser.

Así para\(y > 0\), tenemos\[\vec{k}=\left(k_{x}, k_{y}\right)=\left(\omega / v,\left(\omega^{4} / g^{2}-\omega^{2} / v^{2}\right)^{1 / 2}\right)\]

y\[\vec{k}=\left(k_{x}, k_{y}\right)=\left(\omega / v,\left(\omega^{4} / g^{2}-\omega^{2} / v^{2}\right)^{1 / 2}\right)\]

Esta es la clave de la estela Kelvin. Los diferentes componentes de frecuencia del paquete de olas en el\(y = 0\) viaje en diferentes direcciones a medida que se alejan de la embarcación para\(y > 0\).

Figura\( 14.3\): Una estela construida numéricamente a partir de (14.3) para\(f(\omega)=e^{-\omega^{2} v / g}\).

Figura\( 14.4\): Otra vista de la estela en la Figura\( 14.3\).

Observamos de pasada que la cantidad vectorial\(\vec{k} / \omega\) es muy importante, y probablemente debería tener algún nombre que suene importante. A veces se le llama el “vector de lentitud” en la literatura. Este es el objeto que más naturalmente aparece en la descripción de una onda plana con frecuencia\(\omega\):\[e^{-i \omega(t-\vec{r} \cdot \vec{k} / \omega)}\]

“Vector de lentitud” no me parece captar adecuadamente la relación de esto con la velocidad de fase, por lo que planeo iniciar una campaña para llamar a\(\vec{k} / \omega\) la “segnocidad de fase”\[\vec{s}_{\phi}=\frac{\vec{k}}{\omega}\]

del latín segnis significa lento, porque la segnocidad aumenta en magnitud a medida que los puntos de fase constante en la ola se mueven más lentamente. ⁴ La velocidad de fase en sí misma se puede construir fácilmente a partir de la segnocidad de fase, (14.13), pero realmente es (14.13) lo que aparece naturalmente en las ecuaciones.

Podemos calcular\(f(\omega)\) dada una condición de límite en\(t = y = 0\), y luego construir la estela numéricamente usando (14.3). Para ilustración, considere un gaussiano\(f(\omega)\),\[f(\omega)=e^{-\omega^{2} v / g}\]

lo que corresponde a una perturbación gaussiana a lo largo\(y = 0\). El patrón de estela resultante se muestra en\(Figures \text { } 14.3\) y\(14.4\). ¡Esto parece un velatorio! Así parece que hemos capturado parte de la física esencial de la estela en (14.3).

Pero lo que realmente nos interesa son las propiedades más generales que nos permitirán comprender las características clave de la estela sin ninguna integración numérica. Veremos cómo se propagan los diversos componentes de onda plana. (14.11) implica que las ondas estelares se propagan lejos de\(y = 0\) solo para\[\omega^{2}>g^{2} / v^{2}\]

Ahora necesitamos pensar detenidamente sobre la física de (14.3) y (14.12) - (14.13). En cualquier rango pequeño de\(\omega\), la integración sobre\(\omega\) producirá algún tipo de paquete de olas que se mueve junto con el barco. Diferentes\(\omega\) rangos están asociados con paquetes de ondas que se mueven hacia afuera en diferentes ángulos desde el\(x\) eje. La envolvente de un paquete de ondas en un estrecho rango de frecuencia centrada en\(\omega\) se moverá a la velocidad efectiva del grupo,\(v_{g}\), construida de la siguiente manera\[\vec{s}_{g}=\frac{\partial \vec{k}}{\partial \omega}=\frac{\hat{v}_{g}}{\left|\vec{v}_{g}\right|}=\left(\frac{1}{v}, \frac{2 \omega^{3} / g^{2}-\omega / v^{2}}{\left(\omega^{4} / g^{2}-\omega^{2} / v^{2}\right)^{1 / 2}}\right)\]

y esto determina el ángulo del paquete de ondas en función de\(\omega\). Nuevamente, como con (14.13), el objeto en (14.18) es muy importante y merece un nombre elegante. Voy a llamarlo la “segnocidad grupal”\(\vec{s}_{g}\), porque la envolvente del grupo de olas se mueve más lentamente a medida que\(\vec{s}_{g}\) aumenta. Sugerencias para mejores nombres para\(\vec{s}_{\phi}\) y\(\vec{s}_{g}\) son bienvenidas.

En este punto, el lector puede (justificadamente) preguntarse por qué la velocidad grupal no es la velocidad grupal convencional para las olas de agua,\[V_{g}=\frac{\partial \omega}{\partial k}\]

donde la relación entre\(\omega\) y\(k\) está dada por (14.6) de manera que\[V_{g}=\frac{g}{2 \omega}=\frac{v_{\phi}}{2}\]

Esto da una velocidad de grupo en la misma dirección que la velocidad de fase y apenas la mitad de la magnitud. Para entender la diferencia, debemos generalizar la fórmula para la velocidad de grupo en la sección 10.2.1. Ahí vimos que la forma más sencilla de entender la velocidad grupal es pensar en la superposición de dos ondas planas que están muy juntas en ambas\(\omega\) y\(\vec{k}\)\ [\ begin {reunidas}
\ cos\ izquierda (\ omega_ {1} t-\ vec {k} _ {1}\ cdot\ vec {r}\ derecha) +\ cos\ izquierda (\ omega_ {2} t-\ vec {k} _ {2}\ cdot\ vec {r }\ derecha)\\
=2\ cos\ izquierda (\ frac {\ omega_ {1} -\ omega_ {2}} {2} t-\ frac {\ vec {k} _ {1} -\ vec {k} _ _ {2}} {2}\ cdot\ vec {r}\ derecha)\ cos\ izquierda (\ frac {\ omega_ {} +\ omega_ {2}} {2} t-\ frac {\ vec {k} _ {1} +\ vec {k} _ _ {2}} {2}\ cdot\ vec {r}\ derecha)
\ final {reunido}\]

Si los\(\omega s\) y\(\vec{k} s\) están muy juntos, el primer factor es una envolvente que oscila lentamente, como la envolvente del paquete de onda, con vector de segnocidad\[\vec{s}_{-}=\frac{\vec{k}_{1}-\vec{k}_{2}}{\omega_{1}-\omega_{2}}\]

El segundo factor describe la onda portadora que oscila más rápidamente, con vector de segnocidad\[\vec{s}_{+}=\frac{\vec{k}_{1}+\vec{k}_{2}}{\omega_{1}+\omega_{2}}\]

Si\(\vec{k}_{1}\) y\(\vec{k}_{2}\) surgen de una función suave bien definida\(\vec{k}(\omega)\),\[\vec{k}_{1}=\vec{k}\left(\omega_{1}\right) \quad \text { and } \quad \vec{k}_{2}=\vec{k}\left(\omega_{2}\right)\]

entonces\[\lim _{\omega_{1}, \omega_{2} \rightarrow \omega} \vec{s}_{-}=\vec{s}_{g} \quad \text { and } \quad \lim _{\omega_{1}, \omega_{2} \rightarrow \omega} \vec{s}_{+}=\vec{s}_{\phi}\]

como se esperaba de (14.18). Pero esto depende de lo que se mantenga fijo entre\(\vec{k}_{1}\) y\(\vec{k}_{2}\) como\(\omega\) cambios. El punto es el habitual que en una dimensión, la relación de dispersión determina\(k(\omega)\) hasta un signo. Pero en más de una dimensión, infinitamente muchos\(\vec{k} s\) satisfacen la relación de dispersión para un dado\(\omega\). Debemos especificar exactamente cómo\(k(\omega)\) se determina la función antes de que el límite en (14.25) esté bien definido. Así (14.18) es la fórmula general para la velocidad del grupo. Pero lo que significa la derivada (en más de una dimensión) depende de la situación. La física convencional supone que todos los componentes de frecuencia de la onda están en la misma dirección. Entonces la dirección del\(\vec{k}\) vector no cambia con\(\omega\), y (14.18) reduce a (14.19). ⁵ Pero para una ola impulsada por la embarcación en movimiento, lo que se mantiene fija no es la dirección de las olas, sino el\(x\) componente del vector de segnocidad\(k_{x} / \omega\), porque todos los componentes del paquete de olas se mueven junto con la embarcación que las produce. Entonces la condición (14.9) y la relación de dispersión (14.6) tomadas juntas fuerzan la dirección del\(\vec{k}\) vector a cambiar en función de\(\omega\). Así debemos usar la forma general, (14.18). Como veremos, esto implica que la velocidad efectiva del grupo no sólo tiene una magnitud muy diferente a la convencional (14.20), sino que también la velocidad efectiva del grupo y la velocidad de fase no están ni siquiera en la misma dirección.

Las líneas rojas en la Figura\( 14.5\) muestran la posición del paquete de ondas correspondiente a\(\omega = 1.05 g / v\). Los vectores cian muestran las velocidades de grupo para\(y > 0\) y\(y < 0\). Estos son perpendiculares a las líneas de los paquetes de onda. Si tomamos el origen para ser la posición de la embarcación (ya sea instantáneamente o yendo a un sistema de coordenadas móviles en el que la embarcación está estacionaria en el origen), los puntos\(\vec{r}\) en el paquete de olas satisfacen\[\vec{r} \cdot \hat{v}_{g}=0\]

Figura\( 14.5\): Paquetes de ondas (rojo) y ondas de fase (azul) para\(\omega \approx 1.05 \mathrm{~g} / \mathrm{v}\).

Obsérvese también que debido a (14.18),\[\vec{r} \cdot \frac{\partial \vec{k}}{\partial \omega}=0\]

Pero hay una estructura adicional dentro del paquete de ondas debido a las ondas de fase. Las velocidades de fase son mostradas por los vectores verdes, y no están en la misma dirección que la velocidad del grupo. Así, existen oscilaciones a lo largo del paquete de ondas correspondientes a máximos y mínimos de las ondas de fase. Suponiendo que el máximo ocurre en la posición de la embarcación (que estamos tomando para ser el origen), los otros máximos ocurren en\[\vec{r}_{j} \cdot \vec{k}=-2 \pi j \quad \text { for } j=1 \text { to } \infty\]

Estos máximos representan la interacción de la onda plana con la frecuencia\(omega\) (y moviéndose junto con la embarcación) y el paquete de ondas grupales, por lo que los indicamos en la figura por líneas azules de fase constante perpendicular a\(\vec{k}\).

Ahora podemos construir una imagen de la estela armando estos para la gama de importantes\(\omega\). A medida que\(\omega\) cambia, la dirección de las líneas de paquetes de ondas rojas y las ondas de fase azules cambiarán de acuerdo con (14.27) y (14.12). Porque\(\omega \approx g / v\), los paquetes de ondas son casi horizontales y las ondas de fase se mueven casi horizontalmente. Esto se muestra en la Figura\( 14.6\) para\(\omega=1.001 \mathrm{~g} / \mathrm{v}\): A medida que\(\omega\) aumenta, el ángulo de los paquetes de onda aumenta por un tiempo, dando una situación como la que se muestra en la Figura\( 14.5\). Pero lo interesante es que hay un valor crítico de\(\omega\) que da el ángulo máximo para la velocidad del grupo.

Es particularmente sencillo de analizar (14.18) porque\(\partial k_{x} / \partial \omega\) es constante. La\(\omega\) dependencia de\(\partial k_{y} / \partial \omega\) se muestra en Figura\( 14.7\) Debido a que va al infinito como\(\omega \rightarrow g / v\) y como\(\omega \rightarrow \infty\), en estos dos límites la velocidad del grupo va a cero, y su dirección va a\(\hat{y}\). El mínimo de\(\partial k_{y} / \partial \omega\) corresponde al máximo de\(\left|\vec{v}_{g}\right|\), y también al ángulo máximo de propagación de la onda estela desde la\(y\) dirección. Este ángulo máximo es particularmente importante por dos razones. No solo el ángulo máximo corresponde al borde del

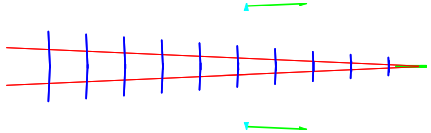
Figura\( 14.6\): Paquetes de ondas (rojo) y ondas de fase (azul) para\(\omega \approx 1.001 \mathrm{~g} / \mathrm{v} .\).

Figura\( 14.7\):

perturbación producida por la embarcación, pero lo que es más importante, en todos los ángulos más pequeños, la energía se extiende sobre los ángulos vecinos. Al máximo, debido a que el ángulo es estacionario con respecto\(\omega\), los vecinos\(\omega\) contribuyen constructivamente y la onda en el borde es genéricamente mucho más intensa que para ángulos más pequeños. ⁶

Para determinar explícitamente el ángulo máximo, nos diferenciamos de\(\partial k_{y} / \partial \omega\) nuevo, lo que da\[\frac{\partial^{2} k_{y}}{\partial \omega^{2}}=\frac{\left(\omega^{2} / g^{2}\right)\left(2 \omega^{4} / g^{2}-3 \omega^{2} / v^{2}\right)}{\left(\omega^{4} / g^{2}-\omega^{2} / v^{2}\right)^{3 / 2}}\]

por lo que el mínimo ocurre en\[\omega^{2}=\frac{3 g^{2}}{2 v^{2}}\]

correspondiente al número de onda\[k=\frac{3 g}{2 v^{2}}\]

y magnitud de la velocidad de fase\[v_{\phi}=\sqrt{\frac{2}{3}} v\]

La dirección de la velocidad de fase es\[\hat{v}_{\phi}=\left(\sqrt{\frac{2}{3}}, \sqrt{\frac{1}{3}}\right)\]

en un ángulo desde el\(x\) eje de\[\theta_{\max }=\arcsin (1 / \sqrt{3})=35.26^{\circ}\]

La longitud de onda es\[\lambda=\frac{4 \pi v^{2}}{3 g}\]

Incluso a bajas velocidades como un metro por segundo (aproximadamente 2 nudos), esta longitud de onda es grande en comparación con la escala (unos pocos centímetros) en la que la tensión superficial adquiere importancia en la relación de dispersión, por lo que (14.6) suele ser una buena aproximación.

Figura\( 14.8\): Paquetes de onda (rojo) y ondas de fase (azul) para el valor crítico\(\omega \approx \sqrt{3 / 2} g / v\).

En el ángulo crítico, nuestros paquetes de ondas y ondas de fase se muestran en la Figura\( 14.8\). A menudo, como en las estelas de la Figura\( 14.1\), las olas de fase a lo largo del ángulo máximo son todo lo que ves.

Para\(\omega\) mayores que\(\sqrt{3 / 2} g / v\), los ángulos del paquete de ondas comienzan a disminuir nuevamente pero las ondas de fase continúan acercándose, como se muestra en la Figura\( 14.9\) para\(\omega=2 g / v\).

Ahora podemos armarlos para un rango que va\(\omega\) desde más\(g / v\) allá del valor crítico. El resultado se muestra en la Figura\( 14.10\). Puede ser más fácil ver lo que está sucediendo si no dibujamos los paquetes de ondas, sino solo las ondas de fase. Estos, después de todo, muestran los lugares donde la oscilación es máxima. El resultado se muestra en la Figura\( 14.11\). Esto da casi lo mismo

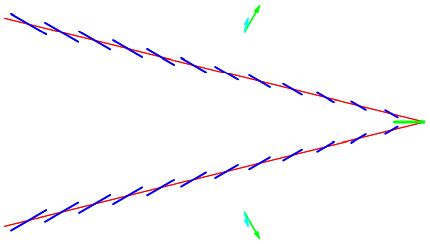
Figura\( 14.9\): Paquetes de onda (rojo) y ondas de fase (azul) para\(\omega \approx 2 g / v .\)

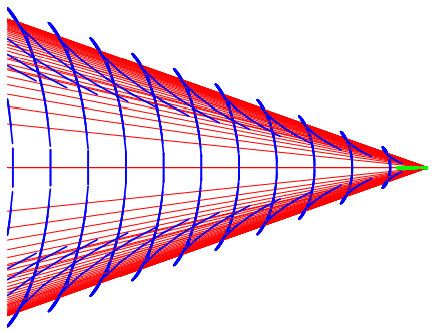
Figura\( 14.10\): Paquetes de ondas combinadas y ondas de fase para un rango de frecuencias.

como una gráfica paramétrica de los puntos en los paquetes de ondas donde las ondas de fase tienen ahí máximos, lo cual se muestra en la Figura\( 14.12\). Deberías ser capaz de reconocer las características básicas de la Figura\( 14.11\) tanto en nuestra construcción numérica, Figura\( 14.3\) como en la bella imagen de una estela real de Wikipedia que se muestra en Figura\( 14.13\) en la página 436. Podemos hacer esto aún más obvio rotando la Figura\( 14.12\) en tres dimensiones, como se muestra en la Figura\( 14.14\). En la estela de la Figura\( 14.13\), las ondas de fase son claramente visibles tanto para las pequeñas\(\omega\) (las ondas que se mueven hacia adelante en el centro) como para las grandes\(\omega\) (las ondas que se mueven hacia afuera y muy poco espaciadas justo dentro del ángulo máximo). De Figura\( 14.11\) y se\(14.13\) debe poder ver por qué las ondas de fase a veces se llaman “ondas plumosas”. La fase ondea para\(\omega>\sqrt{3 / 2} g / v\) lucir como plumas delicadas en el ala de la estela.

Vale la pena hacer un comentario más sobre Figura\( 14.11\). Probablemente ya hayas notado que las ondas de fase encajan juntas en curvas continuas. Esto no es un accidente. Físicamente, por supuesto, la posición en la que la oscilación es máxima ciertamente debe variar

Figura\( 14.11\): Ondas de fase combinadas para un rango de frecuencias.

Figura\( 14.12\): Gráfica paramétrica de los máximos de fase.

continuamente en función de\(\omega\). Pero también, podemos ver que la tangente a la curva que describe los máximos es perpendicular a\(\vec{k}\), y así nuestras ondas de fase en las figuras son solo estas tangentes. Para ver esto, señalar que de (14.27) y (14.28),\(\vec{r}_{j}\) satisface\[\vec{r}_{j} \cdot \vec{k}=-2 \pi j \quad \text { and } \quad \vec{r}_{j} \cdot \frac{\partial \vec{k}}{\partial \omega}\]

Diferenciar el primero con respecto\(\omega\) y usar el segundo da\[\frac{\partial \vec{r}_{j}}{\partial \omega} \cdot \vec{k}=0\]

Figura\( 14.13\): Comparar\(Figures \text { } 14.3 \text {, } 14.11 \text {, } 14.12\) y\(14.14\) con una estela real.

© Fuente desconocida. Todos los derechos reservados. Este contenido está excluido de nuestra licencia Creative Commons. Para obtener más información, consulte https://ocw.mit.edu/help/faq-fair-use.

Figura\( 14.14\): Gráfica paramétrica 3D de los máximos de fase.

que dice que la tangente a la curva descrita paramétricamente por\(\vec{r}_{j}(\omega)\) es perpendicular\(\vec{k}\) y por lo tanto paralela a las ondas de fase. ⁷

2 Esta es una de las muchas bellas fotografías de Ian Alexander - http://easyweb.easynet.co.uk/ iany/patterns/wake.htm.
3 Uno podría, si fuera necesario, mirar solo y > a > 0 para algunos a fijos, esto no cambiaría el análisis de ninguna manera esencial.
4 La inspiración para esto proviene de los paleontólogos, que tienen evidencia fósil para el segnosaurus - “lagarto lento” y también el velocisaurus - “lagarto rápido”.
5 Se ve diferente porque en (14.18) estamos viendo la segnocidad grupal más que la velocidad grupal, pero es un ejercicio elemental en cálculo para llegar de uno a otro.
6 Este apilamiento en un punto estacionario es el mismo fenómeno que escoge el ángulo en el que vemos el arco iris.