5.9: Torsión

En esta sección se describe el concepto de torsión gravitacional. Se puede omitir sin pérdida de continuidad, siempre que acepte la propiedad de simetría\(\Gamma^{a}_{[bc]} = 0\) sin preocuparse por lo que significa físicamente o qué evidencia empírica la sustenta.

Ejercicio\(\PageIndex{1}\)

Autocomprobación: Interpreta el significado matemático de la ecuación\(\Gamma^{a}_{[bc]} = 0\), que se expresa en la notación introducida anteriormente.

¿Los escalares son dependientes de la ruta?

Parece claro que algo así como la derivada covariante es necesaria para los vectores, ya que tienen una dirección en el espacio-tiempo, y así sus medidas varían cuando la medida del espacio-tiempo misma varía. Dado que los escalares no tienen una dirección en el espacio-tiempo, el mismo razonamiento no les aplica, y esto se refleja en nuestras reglas para derivados covariantes. La derivada covariante tiene un\(\Gamma\) término por cada índice del tensor que se está diferenciando, por lo que para un escalar no debería haber\(\Gamma\) términos en absoluto, es decir,\(\nabla_{a}\) es el mismo que\(\partial_{a}\).

Pero solo porque los derivados de los escalares no requieran un tratamiento especial por esta razón en particular, eso no significa que se les garantice que se comporten como esperamos intuitivamente, en el extraño mundo de la relatividad coordinada-invariante.

Una forma posible de que los escalares se comporten de manera contraintuitiva sería por analogía con el transporte paralelo de vectores. Si pegamos un vector en una caja (como con, por ejemplo, los giroscopios a bordo de Gravity Probe B) y lo llevamos alrededor de un bucle cerrado, cambia. ¿Podría pasar lo mismo con un escalar? Esto es extremadamente contradictorio, ya que no hay razón para imaginar tal efecto en ninguno de los modelos que hemos construido de espacios curvos. De hecho, no sólo es contradictorio sino matemáticamente imposible, según el siguiente argumento. La única razón por la que podemos interpretar el efecto vector-in-a-box como derivado de la geometría del espacio-tiempo es que se aplica por igual a todos los vectores. Si, por ejemplo, sólo se aplicara a los vectores de polarización magnética de las sustancias ferromagnéticas, entonces lo interpretaríamos como un campo magnético que vive en el espacio-tiempo, no una propiedad del espacio-tiempo mismo. Si el valor de un escalar en una caja era dependiente de ruta, y esta dependencia de ruta era una propiedad geométrica del espacio-tiempo, entonces tendría que aplicarse a todos los escalares, incluyendo, digamos, masas y cargas de partículas. Por lo tanto, si la masa de un electrón aumentara 1% cuando se transportaba en una caja a lo largo de un cierto camino, su carga también tendría que aumentar 1%. Pero entonces su relación carga-masa seguiría siendo invariante, y esto es una contradicción, ya que la relación carga-masa también es un escalar, y debería haber sentido el mismo efecto de 1%. Dado que la idea variable de escalar en una caja conduce a una contradicción, no fue una coincidencia que no pudiéramos encontrar un modelo que produjera tal efecto; una teoría que carece de autoconsistencia no tiene ningún modelo.

Ejercicio\(\PageIndex{2}\)

Autocomprobación: Explica por qué el transporte paralelo de un vector solo puede girarlo, no cambiar su magnitud.

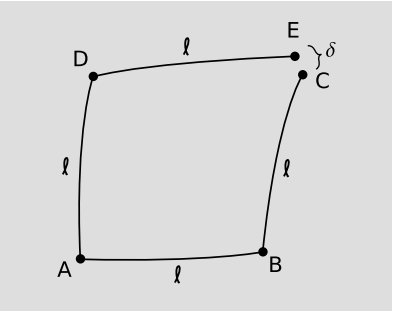
Sin embargo, existe una manera diferente en la que los escalares podrían comportarse de manera contraintuitiva, y esta es matemáticamente autoconsistente. Supongamos que Helen vive en dos dimensiones espaciales y posee un termómetro. Ella quiere medir la variación espacial de la temperatura, en particular su segunda derivada mixta\(\frac{\partial^{2} T}{\partial x \partial y}\). En casa por la mañana en el punto A, se prepara calibrando su girocompás para apuntar al norte y midiendo la temperatura. Después viaja\(\ell\) = 1 km al este por un geodésico hasta B, consulta su girocompás, y gira hacia el norte. Continúa un kilómetro al norte hasta C, toma muestras del cambio de temperatura\(\Delta T_{1}\) con relación a su casa, y luego vuelve a trazar sus pasos para llegar a casa a almorzar. Por la tarde, revisa su trabajo realizando el mismo proceso, pero esta vez intercambia los roles de norte y oriente, viajando por ADE. Si estuviera viviendo en un espacio plano, esto formaría los otros dos lados de un cuadrado, y su muestra de temperatura vespertina\(\Delta T_{2}\) estaría en el mismo punto en el espacio C que su muestra matutina. En realidad no reconoce el paisaje, por lo que los puntos de muestra C y E son diferentes, pero esto solo confirma lo que ya sabía: el espacio no es plano. ¹⁰

Figura\(\PageIndex{1}\) - Medición\(\frac{\partial^{2} T}{\partial x \partial y}\) para una T escalar.

Figura\(\PageIndex{2}\) - Los giroscopios giran ambos cuando se transportan de A a B, provocando que Helen navegue a lo largo de BC, que no forma un ángulo recto con AB. El ángulo entre los ejes de los dos giroscopios es siempre el mismo, por lo que la rotación no es localmente observable, pero sí produce una brecha observable entre C y E.

Nota

Este punto fue mencionado en la sección 5.4, en relación con la definición del tensor Riemann.

Nada de esto parece sorprendente todavía, pero ahora hay dos formas cualitativamente diferentes en las que podría resultar su análisis de sus datos, lo que indica cosas cualitativamente diferentes sobre las leyes de la física en su universo. La definición de la derivada como límite requiere que repita el experimento a escalas más pequeñas. Como\(\ell\) → 0, el resultado para\(\frac{\partial^{2} T}{\partial x \partial y}\) debe acercarse a un límite definido, y el error debe disminuir en proporción a\(\ell\). En particular, la diferencia entre los resultados inferidos\(\Delta T_{1}\) e\(\Delta T_{2}\) indican un error, y la discrepancia entre las segundas derivadas inferidas de ellas debería encogerse adecuadamente a medida que\(\ell\) se encoge. Supongamos que esto no sucede. Dado que los derivados parciales viajan, concluimos que su procedimiento de medición no es lo mismo que una derivada parcial. Llamémosle procedimiento de medición\(\nabla\), para que esté observando una discrepancia entre\(\nabla_{x} \nabla_{y}\) y\(\nabla_{y} \nabla_{x}\). El hecho de que el conmutador\(\nabla_{x} \nabla_{y} − \nabla_{y} \nabla_{x}\) no se desvanezca no puede explicarse por los símbolos de Christoffel, porque lo que está diferenciando es un escalar. Dado que la discrepancia surge enteramente de la falta de\(\Delta T_{1} − \Delta T_{2}\) escala adecuada, la conclusión es que la distancia\(\delta\) entre los dos puntos de muestreo no está escalando tan rápido como esperamos. En nuestros modelos familiares de espacios bidimensionales como superficies incrustadas en tres espacios, siempre tenemos\(\delta \sim \ell^{3}\) para pequeños\(\ell\), pero ella ha encontrado que solo se encoge tan rápido como\(\ell^{2}\).

Para una pista de lo que está pasando, tenga en cuenta que el conmutador\(\nabla_{x} \nabla_{y} − \nabla_{y} \nabla_{x}\) tiene una particular mano hacia él. Por ejemplo, voltea su signo bajo una reflexión a través de la línea y = x Cuando hacemos “paralelos” -vectores de transporte, en realidad no están permaneciendo paralelos. En este universo hipotético, un vector en una caja transportada por una pequeña distancia\(\ell\) gira en un ángulo proporcional a\(\ell\). Este efecto se llama torsión. Aunque no aparece ningún efecto de torsión en nuestros modelos familiares, eso no es porque la torsión carezca de autoconsistencia. Existen modelos de espacios con torsión. En particular, podemos ver que la torsión no conduce al mismo tipo de contradicción lógica que la idea varying-scalar-in-a-box. Dado que todos los vectores se retuercen en la misma cantidad cuando se transportan, los productos internos se conservan, por lo que no es posible poner dos vectores en una caja y obtener la paradoja escalar en una caja viendo cambiar su producto interno cuando se transporta la caja.

Tenga en cuenta que los codos ABC y ADE no son ángulos rectos. Si Helen hubiera traído consigo un par de girocompás, uno para x y otro para y, habría encontrado que el ángulo recto entre los girocompás se conservaba bajo transporte paralelo, pero que un girocompás inicialmente tangente a un geodésico no permanecía así. De hecho, hay dos definiciones inequivalentes de un geodésico en un espacio con torsión. El camino más corto entre dos puntos no es necesariamente el mismo que el camino más recto posible, es decir, el que transporta en paralelo su propio vector tangente.

El tensor de torsión

Dado que la torsión es impar bajo paridad, debe ser representada por un tensor de rango impar, al que llamamos\(\tau^{c}_{ab}\) y definimos de acuerdo con

\[(\nabla_{a} \nabla_{b} - \nabla_{b} \nabla_{a})f = - \tau^{c}_{ab} \nabla_{c} f,\]

donde f es cualquier campo escalar, como la temperatura en la sección anterior. Hay dos formas diferentes en las que un espacio puede ser no euclidiano: puede tener curvatura, o puede tener torsión. Para una discusión completa de cómo manejar las matemáticas de un espacio-tiempo con curvatura y torsión, consulte el artículo de Steuard Jensen en http://www.slimy.com/~steuard/teaching/tutorials/GRtorsion.pdf. Para nuestros propósitos actuales, el principal hecho matemático digno de mención es que la torsión de fuga equivale a la simetría\(\Gamma^{a}_{bc} = \Gamma^{a}_{cb}\) de los símbolos de Christoffel. Usando la notación introducida anteriormente,\(\Gamma^{a}_{[bc]} = 0\) si\(\tau = 0\).

Ejercicio\(\PageIndex{3}\)

Autocomprobación: Utilice un argumento similar al del ejemplo 5 para demostrar que ningún modelo de un espacio de dos espacios incrustado en un espacio de tres puede tener torsión.

_{Generalizando a más dimensiones, el tensor de torsión es impar bajo la reflexión completa del espacio-tiempo x a → −x a, es decir, una inversión de paridad más una inversión de tiempo, PT.}

En la historia anterior, tuvimos una torsión que no conservaba los vectores tangentes. En tres o más dimensiones, sin embargo, es posible tener torsión que sí preserva los vectores tangentes. Por ejemplo, transportar un vector a lo largo del eje x podría causar solo una rotación en el plano y-z. Esto se relaciona con las simetrías del tensor de torsión, que por conveniencia escribiremos en un sistema de coordenadas x-y-z y en la forma totalmente covariante\(\tau_{\lambda \mu \nu}\). La definición del tensor de torsión implica\(\tau_{\lambda (\mu \nu)} = 0\), es decir, que el tensor de torsión es antisimétrico en sus dos índices finales. La torsión que no conserva los vectores tangentes tendrá elementos que no se desvanecen como\(\tau_{xxy}\), lo que significa que el transporte paralelo de un vector a lo largo del eje x puede cambiar su componente x. La torsión que conserva los vectores tangentes tendrá que desaparecer\(\tau_{\lambda \mu \nu}\) a menos que\(\lambda, \mu\), y\(\nu\) sean todas distintas. Este es un ejemplo del tipo de antisimetría que es familiar a partir del producto cruzado vectorial, en el que los productos cruzados de los vectores base se comportan como x × y = z, y × z = x, y × z = x . Generalizando la notación para simetrización y antisimetría de tensores desde antes, tenemos

\[\begin{align} T_{(abc)} &= \frac{1}{3!} \Sigma T_{abc} \\ T_{[abc]} &= \frac{1}{3!} \Sigma \epsilon^{abc} T_{abc}, \end{align}\]

donde las sumas están sobre todas las permutaciones de los índices, y en la segunda línea hemos utilizado el símbolo Levi-Civita. En esta notación, un tensor de torsión totalmente antisimétrico es uno con\(\tau_{\lambda \mu \nu} = \tau_{[\lambda \mu \nu]}\), y la torsión de este tipo conserva los vectores tangentes bajo traducción.

Figura\(\PageIndex{3}\) - Tres giroscopios están inicialmente alineados con los ejes x, y y z. Después del transporte paralelo a lo largo del eje x geodésico, el giroscopio x todavía está alineado con el eje x, pero los giroscopios y y z han girado.

En dos dimensiones, no hay objetos totalmente antisimétricos con tres índices, porque no podemos escribir tres índices sin repetir uno. En tres dimensiones, un objeto antisimétrico con tres índices es simplemente un múltiplo del tensor Levi-Civita, por lo que una torsión totalmente antisimétrica, si existe, está representada por un solo número; bajo traslación, los vectores giran como tornillos diestros o zurdos, y este número nos indica la tasa de rotación. En cuatro dimensiones, tenemos cuatro cantidades independientemente variables,\(\tau_{xyz}, \tau_{tyz}, \tau_{txz}\), y\(\tau_{txy}\). En otras palabras, una torsión antisimétrica de 3+1 espacio-tiempo puede ser representada por un cuatro vectores,\(\tau^{a} = \epsilon^{abcd} \tau_{bcd}\).

Búsquedas experimentales para Torsión

Una forma de afirmar el principio de equivalencia (ver sección 4.4) es que prohíbe que el espacio-tiempo venga equipado con un campo vectorial que podría ser medido por observadores de caída libre, es decir, observadores en marcos locales de Lorentz. Se han realizado diversas pruebas de alta precisión del principio de equivalencia. Desde el punto de vista de un experimentador que realiza este tipo de pruebas, es importante distinguir entre los campos que están “incorporados” al espacio-tiempo y los que viven en el espacio-tiempo. Por ejemplo, la existencia del campo magnético terrestre no viola el principio de equivalencia, pero si un experimento era sensible al campo terrestre, y el experimentador no lo sabía, parecería haber una violación. La torsión antisimétrica en cuatro dimensiones actúa como un vector. Si constituye un efecto de fondo universal integrado en el espacio-tiempo, entonces viola el principio de equivalencia. Si en cambio surge de fuentes materiales específicas, entonces aún puede aparecer como un efecto medible en pruebas experimentales diseñadas para detectar la invarianza de Lorentz. Consideremos esta última posibilidad.

Dado que la curvatura en general la relatividad proviene de la masa y la energía, tal como lo representa el tensor estres-energía T _ab, podríamos preguntarnos cuáles serían las fuentes de torsión, si existe en nuestro universo. La fuente no puede ser el tensor tensión-energía rank-2. Tendría que ser un tensor de rango impar, es decir, una cantidad que es impar bajo PT, y en teorías que incluyen torsión comúnmente se asume que la fuente es el momento angular cuántico-mecánico de partículas subatómicas. Si este es el caso, entonces se espera que los efectos de torsión sean proporcionales a\(\hbar\) G, el producto de la constante de Planck y la constante gravitacional, y por lo tanto deberían ser extremadamente pequeños y difíciles de medir. La teoría de cuerdas, por ejemplo, incluye la torsión, pero nadie ha encontrado la manera de probar empíricamente la teoría de cuerdas porque esencialmente hace predicciones sobre fenómenos en la escala de Planck,\(\sqrt{\frac{\hbar G}{c^{3}}}\) ∼ 10 ⁻³⁵ m, donde tanto la gravedad como la mecánica cuántica son efectos fuertes.

Sin embargo, existen algunos experimentos de alta precisión que tienen una probabilidad razonable de detectar si nuestro universo tiene torsión. La torsión viola el principio de equivalencia, y para el cambio de siglo las pruebas del principio de equivalencia habían alcanzado un nivel de precisión suficiente para descartar algunos modelos que incluyen torsión. La Figura 5.8.4 muestra un péndulo de torsión utilizado en un experimento por el grupo Eöt-Wash de la Universidad de Washington. ¹¹ Si existe torsión, entonces el espín intrínseco\(\boldsymbol{\sigma}\) de un electrón debería tener una energía\(\boldsymbol{\sigma} \cdot \boldsymbol{\tau}\), donde\(\boldsymbol{\tau}\) está la parte espacial del vector de torsión. La torsión podría ser generada por la tierra, el sol o algún otro objeto a mayor distancia. La interacción\(\boldsymbol{\sigma} \cdot \boldsymbol{\tau}\) modificará el comportamiento de un péndulo de torsión si los espines de los electrones en el péndulo están polarizados de forma no aleatoria, como en un material magnético. El péndulo tenderá a preceder alrededor del eje definido por\(\boldsymbol{\tau}\).

Figura\(\PageIndex{4}\) - El péndulo de torsión de la Universidad de Washington utilizado para buscar torsión. Las cuñas gris claro son Alnico, las más oscuras SmCo5. Las flechas con las cabezas rellenas representan las direcciones de los espines de electrones, con flechas más densas que indican mayor polarización. Las flechas con las cabezas abiertas muestran la dirección del campo B.

Este tipo de experimento es extremadamente difícil, ya que el péndulo tiende a actuar como una brújula magnética ultrasensible, resultando en una medición del campo magnético ambiental en lugar del hipotético campo de torsión\(\boldsymbol{\tau}\). Para eliminar esta fuente de error sistemático, el grupo UW primero eliminó el campo magnético ambiental lo mejor posible, utilizando blindaje mu-metal y bobinas Helmholtz. También construyeron el péndulo a partir de una combinación de dos materiales magnéticos, Alnico 5 y SmCo ₅, de tal manera que el momento dipolo magnético desapareció, pero el momento dipolo de espín no lo hizo; el campo magnético de Alnico 5 se debe casi en su totalidad al espín electrónico, mientras que el campo magnético de SmCo ₅ contiene contribuciones significativas del movimiento orbital. El resultado fue un objeto no magnético cuyos espines fueron polarizados. Después de cuatro años de recolección de datos, encontraron\(|\boldsymbol{\tau}| \lesssim 10^{−21}\) eV. Los modelos que incluyen torsión suelen predecir que tales efectos son del orden de\(\frac{m^{2}_{e}}{m_{P}} ∼ 10^{−17}\) eV, donde m _e es la masa del electrón y\(m_{P} = \sqrt{\frac{\hbar c}{G}}\) ≈ 10 ¹⁹ GeV ≈ 20\(\mu\) g es la masa de Planck. Por lo tanto, estos experimentos descartan una amplia clase de estos modelos.

Dado que no parece haber evidencia experimental de la existencia de torsión gravitacional en nuestro universo, asumiremos a partir de ahora que desaparece de manera idéntica. Einstein hizo la misma suposición cuando originalmente creó la relatividad general, aunque él y Cartan luego retocaron con teorías no libres de torsión en un intento fallido de unificar la gravedad con el electromagnetismo. Algunos modelos que incluyen torsión siguen siendo viables. Por ejemplo, se ha argumentado que el tensor de torsión debería caerse rápidamente con la distancia de la fuente. ¹²

Referencias

¹¹ http://arxiv.org/abs/hep-ph/0606218

¹² Carroll y Field, http://arxiv.org/abs/gr-qc/9403058