3.4: Cálculo multivariado

¿Qué hace una sección sobre cálculo multivariado en un libro de física.. particularmente un libro de física que asume que ya conoces el cálculo multivariado? La respuesta es que pasaste por tu curso de cálculo multivariado aprendiendo un tema tras otro, y hay algunos temas sutiles que cubriste al principio del curso que realmente no se podían entender correctamente hasta que no habías cubierto otros temas que vinieron más adelante en el curso. (Esto no es culpa de tu profesor en el cálculo multivariado, porque los temas posteriores no podrían entenderse en absoluto sin una exposición a los temas anteriores.) Esta sección se remonta e investiga cinco puntos sutiles del cálculo multivariado para asegurarse de que no te hagan tropezar cuando se aplican a la termodinámica.

3.4.1 ¿Qué es una derivada parcial?

Dada una función f (x, y, z), ¿cuál es el significado de f /y? Muchos responderán a eso

\[\frac{\partial f}{\partial y} \text { is the change of } f \text { with } y \text { while everything else is held constant. }\]

¡Esta respuesta es INCORRECTA! Si f cambia, entonces f ² cambia, y el pecado (f) cambia, y así sucesivamente, así que no puede ser que “todo lo demás” se mantenga constante. La respuesta correcta es que

\[\frac{\partial f}{\partial y} \text { is the change of } f \text { with } y \text { while all other variables are held constant. }\]

De esta manera se vuelve esencial mantener claro qué cantidades son variables y cuáles son funciones. Esto no suele ser difícil en el contexto de las matemáticas: las funciones son f, g y h mientras que las variables son x, y y z. Pero en el contexto de la física utilizamos símbolos como E, V, p, T y N que sugieren las cantidades que representan, y es fácil mezclar las funciones y las variables.

Una ilustración a partir de la geometría hace que este punto sea muy bien. Considera el conjunto de todos los cilindros circulares correctos. Cada cilindro se puede especificar de forma única por las variables r, radio y h, altura. Si conoce r y h para un cilindro, puede calcular fácilmente cualquier cantidad de interés, como el área de la parte superior, T (r, h), el área del lado S (r, h) y el volumen V (r, h), como se muestra en el lado izquierdo de la tabla abajo. Pero esta no es la única manera de especificar cada cilindro de manera única. Por ejemplo, si conoce la altura y el área lateral del cilindro, puede calcular fácilmente el radio y, por lo tanto, encontrar nuestra especificación anterior. En efecto, la especificación a través de las variables S y h es igual de buena como la que pasa por las variables r y h, como se muestra en el lado derecho de la tabla siguiente. [Hay muchas otras especificaciones posibles (por ejemplo, r y S, o T y V) pero estos dos conjuntos serán suficientes para hacer nuestro punto.]

Describir un cilindro

\( \begin{array}{cl}{\textbf{ variables: }} & {\textbf{ variables: }} \\ {\text { radius } r} & {\text { side area } S} \\ {\text { height } h} & {\text { height } h} \\ {\textbf{ functions: }} & {\textbf{ functions: }} \\ {\text { top area } T(r, h)=\pi r^{2}} & {\text { radius } r(S, h)=S / 2 \pi h} \\ {\text { side area } S(r, h)=2 \pi r h} & {\text { top area } T(S, h)=S^{2} / 4 \pi h^{2}} \\ {\text { volume } V(r, h)=\pi r^{2} h} & {\text { volume } V(S, h)=S^{2} / 4 \pi h}\end{array}\)

Todo esto es bastante sencillo y ordinario. Pero ahora hacemos una pregunta más sobre la geometría de los cilindros, a saber, “¿Cómo cambia el volumen con la altura?” La última línea de la tabla presenta dos fórmulas para el volumen, por lo que tomar derivado apropiado nos da ya sea

\[\frac{\partial V}{\partial h}=\pi r^{2}=T \quad \text { or } \quad \frac{\partial V}{\partial h}=-S^{2} / 4 \pi h^{2}=-T.\]

¿Qué? ¿Es V /h igual a T o a − T? ¡No puede ser igual a ambos! El problema con la ecuación (3.11) es que fuimos descuidados al especificar las variables. Las dos expresiones para volumen,

\[V(r, h)=\pi r^{2} h \quad \text { and } \quad V(S, h)=S^{2} / 4 \pi h,\]

son de hecho dos funciones completamente diferentes, con variables completamente diferentes, por lo que debemos esperar derivadas completamente diferentes. Si aumentamos la altura h manteniendo fijo el radio r, la cifra de abajo a la izquierda deja claro que el volumen aumenta. Pero si aumentamos la altura y mantenemos fija el área lateral S, el radio tendrá que disminuir como se muestra a la derecha de abajo. El cambio de la derecha se suma al volumen en la parte superior del cilindro pero resta del volumen a lo largo de los lados. Lo más destacable sería que los dos cambios de volumen fueran iguales y, como han demostrado nuestros derivados, no lo son.

Un matemático diría que nos metimos en problemas en la ecuación (3.11) porque le dimos el mismo nombre a dos funciones distintas. Un físico respondería que ambos representan el volumen, por lo que merecen el mismo nombre. En lugar de entrar en un argumento, lo mejor es escribir explícitamente las variables de todas las funciones, reescribiendo así (3.11) como

\[\frac{\partial V(r, h)}{\partial h}=\pi r^{2}=T(r, h) \quad \text { or } \quad \frac{\partial V(S, h)}{\partial h}=-S^{2} / 4 \pi h^{2}=-T(S, h).\]

(Los físicos a menudo descuidan escribir la lista completa de variables, lo que ahorra algo de tiempo y algo de tinta pero que invita al error. R.H. Price y J.D. Romano (Am. J. Phys. 66 (1998) 114) exponen una situación en la que un físico publicó un profundo error, que cometió al descuidar escribir una lista explícita de variables.)

Se vuelve tedioso escribir toda la lista de argumentos para cada función, por lo que se ha desarrollado una notación taquigráfica. Un paréntesis derecho se escribe después de la derivada parcial, y los argumentos funcionales que no se están diferenciando se enumeran como subíndices a ese paréntesis. Así, las derivadas anteriores se escriben como

\[\frac{\partial V(r, h)}{\partial h}=\frac{\partial V}{\partial h} )_{r} \quad \text { and } \quad \frac{\partial V(S, h)}{\partial h}=\frac{\partial V}{\partial h} )_{S}.\]

La expresión de la izquierda se lee “la derivada parcial de V con respecto a h mientras r se mantiene constante”.

3.4.2 La transformación de Legendre

Volvamos a una descripción de cilindros en términos de las variables r y h. Claramente, una de las funciones de interés es el volumen

\[V (r, h).\]

Un vistazo a la tabla de la página 58 (o el pensamiento de un momento sobre la geometría) muestra que el diferencial total de V en función de r y h es

\[d V=S(r, h) d r+T(r, h) d h,\]

de donde

\[S(r, h)=\frac{\partial V}{\partial r} )_{h} \quad \text { and } \quad T(r, h)=\frac{\partial V}{\partial h} )_{r}.\]

Así, el conocimiento de la función V (r, h) nos da un bono... si conocemos V (r, h), entonces podemos tomar derivadas simples para encontrar las otras cantidades de interés concernientes a los cilindros, es decir, S (r, h) y T (r, h). Debido a la importancia central de V (r, h), se le llama “función maestra” y al diferencial total (3.16) se le llama “ecuación maestra”.

¿Hay alguna manera de encontrar una “descripción maestra” igualmente conveniente en términos de las variables S y h? En efecto la hay, y está dada por la “transformación de Legendre”. En la transformación de Legendre de las variables r y h a las variables S y h, cambiamos el foco de nuestra atención de la función maestra V (r, h) a la función

\[\Phi(S, h)=V(r(S, h), h)-S r(S, h).\]

(La ecuación anterior se escribe en su totalidad con todos los argumentos mostrados. Se suele ver como

\[\Phi=V-S r,\]

aunque esta forma plantea la posibilidad de que variables y funciones se mezclen.) El diferencial total de Φ es

\[d \Phi =d V-S d r-r d S\]

\[ =S d r+T d h-S d r-r d S\]

\[ =-r d S+T d h\]

¡Hemos encontrado una nueva función maestra! Es

\[\Phi(S, h),\]

y la nueva ecuación maestra es

\[d \Phi=-r(S, h) d S+T(S, h) d h,\]

dando lugar de inmediato a

\[r(S, h)=-\frac{\partial \Phi}{\partial S} )_{h} \quad \text { and } \quad T(S, h)=\frac{\partial \Phi}{\partial h} )_{S}.\]

Esta descripción tiene todas las características de una descripción maestra: una vez que se conoce la función maestra, todas las demás funciones interesantes se pueden encontrar tomando derivadas directas.

3.4.3 Relaciones Maxwell

Supongamos

\[df = A(x, y) dx + B(x, y) dy. (3.26)\]

Entonces

\(A(x, y)=\frac{\partial f}{\partial x} )_{y} \quad \text { and } \quad B(x, y)=\frac{\partial f}{\partial y} )_{x}.\)

Pero porque

\(\frac{\partial^{2} f(x, y)}{\partial x \partial y}=\frac{\partial^{2} f(x, y)}{\partial y \partial x}\)

se deduce que

\[\frac{\partial A}{\partial y} )_{x}=\frac{\partial B}{\partial x} )_{y}.\]

A esto se le llama una “relación Maxwell”.

Aplicado a la ecuación (3.16), esto nos dice de un vistazo que

\[\frac{\partial S}{\partial h} )_{r}=\frac{\partial T}{\partial r} )_{h}.\]

¡Sabemos que estos dos derivados son iguales sin necesidad de encontrar a ninguno de ellos! Aplicada a la ecuación (3.24), nos dice con igual facilidad que

\[ \frac{\partial r}{\partial h} )_{S}=-\frac{\partial T}{\partial S} )_{h}.\]

3.4.4 Teorema de la función implícita

Supongamos que f (x, y) es una función de las variables x e y. Qué es

\[\frac{\partial y}{\partial x} )_{f}\]

la pendiente de un contorno de f constante?

Empezar con

\[d f=\frac{\partial f}{\partial x} )_{y} d x+\frac{\partial f}{\partial y} )_{x} d y.\]

que se mantiene para cualquier cambio diferencial dx y dy. Pero no nos interesa ningún cambio diferencial: para evaluar la pendiente (3.30), necesitamos un cambio en el que df = 0 así

\( 0=\frac{\partial f}{\partial x} )_{y} d x+\frac{\partial f}{\partial y} )_{x} d y \quad \text { with } d x, d y \text { on contour of } f.\)

Así

\(\frac{d y}{d x}=-\frac{\frac{\partial f}{\partial x} )_{y}}{\frac{\partial f}{\partial y} )_{x}} \quad \text { with } d x, d y \text { on contour of } f\)

y, escribiendo la restricción “con dx, dy en contorno de f” en los símbolos de la ecuación,

\[\frac{\partial y}{\partial x} )_{f}=-\frac{\frac{\partial f}{\partial x} )_{y}}{\frac{\partial f}{\partial y} )_{x}}.\]

Tenga en cuenta que obtiene la respuesta incorrecta si “cancela la pequeña cantidad f del numerador y denominador de la relación”. Eso es porque “la pequeña cantidad f con y constante” es diferente de “la pequeña cantidad f con constante x”. Necesito escribir algunas palabras y una cifra sobre por qué.

3.4.5 Regla de cadena multivariante

Supongamos que f (x, y) y g (x, y) son dos funciones de las variables x e y. Entonces otra vez tenemos

\[d f=\frac{\partial f}{\partial x} )_{y} d x+\frac{\partial f}{\partial y} )_{x} d y\]

para cualquier cambio diferencial dx y dy.

¿Y si nos interesa, no en ningún cambio, sino en un cambio a lo largo de un contorno de g constante? Específicamente, ¿y si necesitamos encontrar el cambio de f con x mientras nos movemos sobre un contorno de g constante? Entonces solo toma el diferencial exacto arriba y aplícalo a un cambio dx, dy a lo largo del contorno con g constante. Dividir por la cantidad diferencial dx:

\(\frac{d f}{d x}=\frac{\partial f}{\partial x} )_{y} \frac{d x}{d x}+\frac{\partial f}{\partial y} )_{x} \frac{d y}{d x}=\frac{\partial f}{\partial x} )_{y}+\frac{\partial f}{\partial y} )_{x} \frac{d y}{d x} \quad \text { with } d x, d y \text { on contour of } g\)

Ahora escribe la restricción “con dx, dy en contorno de g” en los símbolos de la ecuación para encontrar

\[\frac{\partial f}{\partial x} )_{g}=\frac{\partial f}{\partial x} )_{y}+\frac{\partial f}{\partial y} )_{x} \frac{\partial y}{\partial x} )_{g},\]

la regla de la cadena multivariante.

Problemas

3.9 Derivadas parciales en el espacio

Un punto en el plano puede ser especificado ya sea por las variables (x, y) o por las variables (x ', y') donde

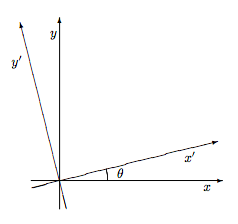
\[\begin{aligned} x^{\prime} &=+\cos (\theta) x+\sin (\theta) y \\ y^{\prime} &=-\sin (\theta) x+\cos (\theta) y \end{aligned}.\]

Si f (x, y) es alguna función de la ubicación en el plano, entonces escriba expresiones para

\[\frac{\partial f}{\partial x^{\prime}} )_{y^{\prime}}, \quad \frac{\partial f}{\partial y^{\prime}} )_{x^{\prime}}, \quad \text { and } \quad \frac{\partial f}{\partial x} )_{y^{\prime}}\]

en términos de

\[\frac{\partial f}{\partial x} )_{y} \quad \text { and } \quad \frac{\partial f}{\partial y} )_{x}.\]

Interpretar f /x) _y' geométricamente como una derivada direccional. (Es decir, f /x) _y' es la pendiente de f a lo largo de cual curva en el plano?) Dada esta interpretación, ¿tiene los límites esperados como θ → 0 y como θ → π/2?

3.10 Relaciones Maxwell para un sistema de tres variables

Supongamos que Φ (x, y, z) satisface

\[d \Phi=A(x, y, z) d x+B(x, y, z) d y+C(x, y, z) d z.\]

Declarar tres relaciones Maxwell relacionando varias primeras derivadas de A (x, y, z), B (x, y, z) y C (x, y, z), y una cuarta relación Maxwell que relaciona varias segundas derivadas de estas funciones.

3.11 El modelo de cilindro con tres variables

En el “modelo de cilindros de tres variables” los cilindros se describen por altura h, radio r y densidad ρ. La función maestra es masa M (h, r, ρ), y la ecuación maestra es

\[d M(h, r, \rho)=\rho S(h, r) d r+\rho T(r) d h+V(h, r) d \rho ,\]

donde S (h, r) es el área lateral, T (r) es el área superior y V (h, r) es el volumen. Realizar una transformación de Legendre a una descripción en términos de las variables h, S y ρ usando la nueva función maestra

\[\Phi(h, S, \rho)=M-\rho S r.\]

a. Anote la nueva ecuación maestra.

b. Anote las tres relaciones Maxwell de primer orden y confirme su corrección utilizando fórmulas explícitas como M (h, S, ρ) = ρS ²/(4π h).

c. Interpretar Φ (h, S, ρ) físicamente.

3.12 Regla de cadena multivariante

Inventar un problema pasando por el argumento de regla de cadena de la sección 3.8.1 con el modelo de cilindro.

3.13 Contornos de área lateral constante

Encontrar contornos de área lateral constante preparándose para/usando la técnica de la sección 3.8.3.