1: ¿Qué es la Lógica?
- Page ID
- 102767
Existe una visión antigua, aún ampliamente difundida, de que lo que hace que los seres humanos sean especiales —lo que nos distingue de las “bestias del campo ”— es que somos racionales. ¿En qué consiste la racionalidad? Esa es una pregunta molesta, pero una posible respuesta va más o menos así: manifestamos nuestra racionalidad al dedicarnos a actividades que implican el razonamiento —hacer afirmaciones y respaldarlas con razones, actuar de acuerdo con las razones y creencias, extraer inferencias de las pruebas disponibles, etc.
Esta actividad de razonamiento se puede hacer bien y se puede hacer mal; se puede hacer correcta o incorrectamente. La lógica es la disciplina que pretende distinguir el buen razonamiento del mal.
El buen razonamiento no es necesariamente un razonamiento efectivo. De hecho, como veremos en un capítulo posterior sobre falacias lógicas, el mal razonamiento es omnipresente y a menudo extremadamente efectivo, en el sentido de que a menudo la gente es persuadida por ello. En la lógica, el estándar de bondad no es la efectividad en el sentido de persuasión, sino la corrección según reglas lógicas.
Por ejemplo, consideremos a Hitler. Convenció a toda una nación para que acompañara una variedad de propuestas que no sólo eran falsas sino francamente malvadas. No te sorprenderá escuchar que si lo examinas críticamente, su razonamiento no pasa de reunión lógica. Los argumentos de Hitler fueron efectivos, pero no lógicamente correctos. Además, sus técnicas persuasivas van más allá del razonamiento en el sentido de respaldar las afirmaciones con razones. Hitler confió en amenazas, manipulación emocional, aseveraciones sin fundamento, etc. Hay muchos trucos retóricos que uno puede usar para persuadir.
En lógica, estudiamos las reglas y técnicas que nos permiten distinguir el razonamiento bueno, correcto del razonamiento malo, incorrecto.
Dado que existen una variedad de diferentes tipos de razonamiento y métodos con los que evaluar cada uno de estos tipos, además de diversas opiniones divergentes sobre lo que constituye el razonamiento correcto, existen muchos enfoques para la empresa lógica. Hablamos de lógica, pero también de lógicas. Una lógica es solo un conjunto de reglas y técnicas para distinguir el buen razonamiento del mal. Una lógica debe formular estándares precisos para evaluar el razonamiento y desarrollar métodos para aplicar esos estándares a instancias particulares.
Nociones Básicas
El razonamiento implica afirmaciones o declaraciones, haciéndolas y respaldarlas con razones, exponiendo sus consecuencias. Las proposiciones son las cosas que reclamamos, declaramos, afirmamos.
Las proposiciones son el tipo de cosas que pueden ser verdaderas o falsas. Se expresan mediante sentencias declarativas. Utilizamos tales frases para hacer todo tipo de aseveraciones, desde asuntos rutinarios de hecho (“la Tierra gira alrededor del Sol”), hasta grandes tesis metafísicas (“la realidad es un Absoluto inmutable, sin rasgos, unificado”), hasta afirmaciones sobre moralidad (“está mal comer carne”).
Es importante distinguir oraciones en el estado de ánimo declarativo, que expresan proposiciones, de oraciones en otros estados de ánimo, que no. Las oraciones interrogativas, por ejemplo, hacen preguntas (“¿Está lloviendo?”) , y las oraciones imperativas emiten órdenes (“No beba queroseno.”). No tiene sentido preguntarse si este tipo de oraciones expresan verdades o falsedades, para que no expresen proposiciones.
También distinguimos proposiciones de las oraciones que las expresan, porque una sola proposición puede ser expresada por oraciones diferentes. “Está lloviendo” y “es regnet” ambos expresan la proposición de que está lloviendo; una frase lo hace en inglés y la otra en alemán. También, “Juan ama a María” y “María es amada por Juan” ambos expresan la misma proposición.
La unidad fundamental del razonamiento es el argumento. En lógica, por “argumento” no nos referimos a un desacuerdo, a un partido de gritos; más bien, definimos el término precisamente:
Argumento = un conjunto de proposiciones, una de las cuales, la conclusión, es (se supone que debe estar) sustentada por las otras, las premisas.
Si estamos razonando haciendo afirmaciones y respaldándolas con razones, entonces la afirmación que se está respaldando es la conclusión de un argumento; las razones dadas para apoyarlo son las premisas del argumento. Si estamos razonando dibujando una inferencia de un conjunto de afirmaciones, entonces la inferencia que sacamos es la conclusión de un argumento, y las declaraciones de las que se extrae son las premisas.
Incluimos la cobertura entre paréntesis —“ se supone que es ”— en la definición para dar cabida a malos argumentos. Un mal argumento, en términos muy generales, es aquel en el que las premisas no apoyan la conclusión; las premisas de un buen argumento realmente apoyan la conclusión.
Análisis de Argumentos
El siguiente pasaje expresa un argumento:
No deberías comer en McDonald's. ¿Por qué? En primer lugar, porque pagan a sus trabajadores salarios muy bajos. Segundo, los animales que proporcionan su carne son criados en condiciones deplorables. Por último, la comida es extremadamente insalubre.
Así lo hace este pasaje:
El universo es vasto y complejo. Y sin embargo, ¿no muestra también un asombroso grado de orden? Los planetas orbitan el sol de acuerdo con las leyes regulares, y las partes más minúsculas de los animales están dispuestas precisamente para servir a sus propósitos. Tal orden y complejidad no pueden surgir al azar. Por lo tanto, el universo debe ser producto de un Diseñador de enorme poder e intelecto, a quien llamamos Dios.
Nuevamente, el propósito último de la lógica es evaluar argumentos, distinguir lo bueno de lo malo. Para ello se requieren distinciones, definiciones, principios y técnicas que se esbozarán en capítulos posteriores. Por ahora, nos enfocaremos en identificar y reconstruir argumentos.
La primera tarea es explicar argumentos—exponer explícitamente sus premisas y conclusiones. Una manera perspicaz de hacerlo es simplemente enumerar oraciones declarativas que expresen las proposiciones pertinentes, con una línea que separe las premisas de la conclusión, así:
- McDonald's paga a sus trabajadores salarios muy bajos.
- Los animales que proporcionan carne de McDonald's son criados en condiciones deplorables.
- La comida de McDonald's es muy poco saludable.
No deberías comer en McDonald's. [1]
Esta es una explicación del primer pasaje argumentativo anterior. Para identificar la conclusión de un argumento, es útil preguntarse: “¿Qué está tratando esta persona de convencerme de que crea diciendo estas cosas? ¿Cuál es el punto final de este pasaje?” La respuesta es bastante clara en este caso. Otra pista sobre lo que está pasando en el pasaje la proporciona la palabra “porque” en la tercera oración. Junto con otras palabras, como “desde” y “para”, indica la presencia de una premisa. Podemos llamar a tales palabras marcadores de premisa. El símbolo “/” puede leerse como taquigrafía de “por lo tanto”. Junto con expresiones como “consecuentemente”, “así”, “se deduce eso” y “lo que implica eso”, “por lo tanto” es un indicador de que la conclusión del argumento está a punto de seguir. Llamamos a tales locuciones marcadores de conclusión. Tal marcador no está presente en el primer argumento, pero sí vemos uno en el segundo, que puede explicarse así:
- El universo es vasto y complejo.
- El universo muestra un asombroso grado de orden.
- Los planetas orbitan el sol según las leyes regulares.
- Las partes más minuciosas de los animales están dispuestas precisamente para servir a sus propósitos.
- Tal orden y complejidad no pueden surgir al azar.
El universo debe ser producto de un diseñador de enorme poder e intelecto: Dios.
Varios puntos de comparación con nuestra primera explicación son dignos de mención aquí. Primero, como se mencionó, fuimos alertados de la conclusión por la palabra “por lo tanto”. Segundo, este pasaje requirió mucho más paráfrasis que el primero. La segunda frase es interrogativa, no declarativa, por lo que no expresa una proposición. Dado que los argumentos son, por definición, colecciones de proposiciones, debemos limitarnos a las oraciones declarativas a la hora de explicarlas. Dado que la respuesta a la pregunta retórica de la segunda frase es claramente “sí”, parafraseamos como se muestra. La tercera frase expresa dos proposiciones, por lo que en nuestra explicación las separamos; cada una es una premisa.
Entonces, a veces, cuando explicamos un argumento, tenemos que tomar lo que está presente en el pasaje argumentativo y cambiarlo ligeramente, para que todas las frases que escribimos expresen las proposiciones presentes en el argumento. Esto es parafrasear. En otras ocasiones, tenemos que hacer aún más. Por ejemplo, tal vez tengamos que introducir proposiciones que no se mencionan explícitamente dentro del pasaje argumentativo, sino que indudablemente se utilizan dentro del razonamiento del argumento.
Hay una palabra griega para pasajes argumentativos que dejan ciertas proposiciones sin enunciar: enthymemes. Aquí hay un ejemplo:
No puede haber un Dios todo amoroso, porque tantas personas inocentes en todo el mundo están sufriendo.
Aquí hay una premisa implícita que acecha en el fondo, algo que no se ha dicho, pero que necesita ser cierta para que el argumento pase por él. Necesitamos una afirmación que conecte la premisa con la conclusión, que cierre la brecha entre ellas. Algo como esto: Un Dios todo amoroso no permitiría que personas inocentes sufran. O tal vez: el sufrimiento generalizado es incompatible con la idea de una deidad totalmente amorosa. La premisa apunta al sufrimiento, mientras que la conclusión es sobre Dios; estas proposiciones conectan esas dos afirmaciones. Una explicación completa del pasaje argumentativo haría explícita una proposición como esta:
- Muchas personas inocentes en todo el mundo están sufriendo.
- Un Dios todo amoroso no permitiría que sufrieran personas inocentes.
No puede haber un Dios todo amoroso.
Esta es la marca del tipo de premisas tácitas que queremos destapar: si son falsas, socavan el argumento. A menudo, premisas como esta no están declaradas por alguna razón: son afirmaciones polémicas por sí mismas, que requieren pruebas para apoyarlas; así que el arguer las deja fuera, prefiriendo no empantanarse. [2] Sin embargo, cuando los sacamos, podemos forzar un intercambio dialéctico más robusto, enfocando el argumento en el corazón de la materia. En este caso, estaría en orden una discusión sobre la compatibilidad de la bondad y el mal de Dios en el mundo. Hay mucho que decir sobre ese tema. Filósofos y teólogos han desarrollado argumentos elaborados a lo largo de los siglos para defender la idea de que la bondad de Dios y el sufrimiento humano son, de hecho, compatibles. [3]
Hasta el momento, nuestro análisis de argumentos no ha sido particularmente profundo. Hemos señalado la importancia de identificar la conclusión y exponer con claridad las premisas, pero no hemos indagado en las formas en que conjuntos de premisas pueden sustentar sus conclusiones. Nos limitamos a señalar que, colectivamente, las premisas dan apoyo a las conclusiones. No hemos mirado cómo lo hacen, qué tipo de relaciones tienen entre ellos. Esto requiere un análisis más profundo.
A menudo, diferentes premisas apoyarán una conclusión —u otra pretensión— de manera individual, sin la ayuda de ninguna otra. Considera este simple argumento:
① La invasión estadounidense a Irak fue un acto de agresión, no de autodefensa. Además, ② no era razonable esperar que los beneficios de la guerra superaran los inevitables horrores que desataría. Por lo tanto, ③ la Guerra de Irak no fue una guerra justa.
Las proposiciones 1 y 2 apoyan la conclusión, la proposición 3, y lo hacen de manera independiente. Cada uno nos da una razón para creer que la guerra fue injusta, y cada uno se erige como una razón aunque supongamos que la otra no era cierta; esta es la marca de premisas independientes.
Puede ser útil, especialmente cuando los argumentos son más complejos, dibujar diagramas que representen las relaciones entre premisas y conclusión. Podríamos representar el argumento anterior de la siguiente manera:
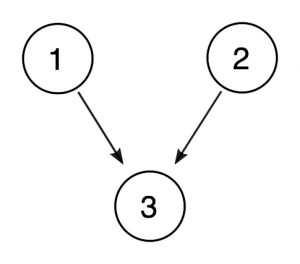
En dicho diagrama, los números en círculo representan las proposiciones y las flechas representan la relación de apoyo de una proposición a otra. Dado que las proposiciones 1 y 2 cada una apoyan 3 de manera independiente, obtienen sus propias flechas.
Otras relaciones entre premisas son posibles. En ocasiones, las premisas dan soporte a conclusiones sólo indirectamente, al darnos una razón para creer alguna otra premisa, que es intermedia entre las dos pretensiones. Considera el siguiente argumento:
① Los poetas son meros “imitadores” cuyas obras oscurecen la verdad; de ahí, ② tienen una influencia corruptora en las almas de los ciudadanos. ③ Por lo tanto, los poetas deben ser excluidos de la ciudad-estado ideal. [4]
En este ejemplo, la proposición 1 da soporte a la proposición 2 (la palabra “por lo tanto” es una pista), mientras que la proposición 2 apoya directamente la conclusión en 3. Representaríamos así las relaciones entre estas proposiciones:

En ocasiones las premisas deben trabajar juntas para dar sustento a otro reclamo, no porque uno de ellos brinde razón para creer al otro, sino porque ninguno brinda el apoyo necesario por sí solo; llamamos a tales proposiciones premisas conjuntas. Considera lo siguiente:
① Si la verdadera inteligencia artificial es posible, entonces uno debe ser capaz de programar una computadora para que sea consciente. ② Pero es imposible programar la conciencia. Por lo tanto, ③ la verdadera inteligencia artificial es imposible.
En este argumento, ni la premisa 1 ni la premisa 2 sustentan la conclusión por sí sola; más bien, la segunda premisa, por así decirlo, proporciona una clave que desbloquea la conclusión de la premisa condicional 1. Podemos indicar dicha interdependencia diagramáticamente con corchetes, así:
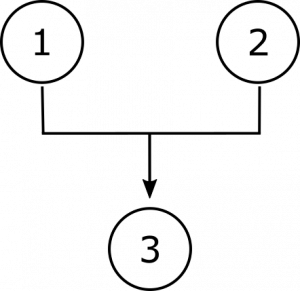
Diagramar argumentos de esta manera puede ser útil tanto para comprender cómo funcionan como para informar cualquier intento de involucrarse críticamente con ellos. Se puede ver claramente en el primer argumento que cualquier consideración planteada contraria a una de las premisas independientes no socavará completamente el apoyo a la conclusión, ya que todavía hay otra premisa que le proporciona algún grado de apoyo. En el segundo argumento, sin embargo, razones que se oponen a la segunda premisa cortarían el apoyo a la conclusión en su raíz; y cualquier cosa contraria a la primera premisa dejará a la segunda necesitada de apoyo. Y en el tercer argumento, consideraciones contrarias a cualquiera de las premisas conjuntas socavarán el apoyo a la conclusión. Especialmente cuando los argumentos son más complejos, tales ayudas visuales pueden ayudarnos a reconocer todas las inferencias contenidas dentro del argumento.
Quizás sea útil concluir considerando un argumento un poco más complejo. Consideremos la naturaleza de los números:
① Los números son objetos abstractos o concretos. ② No pueden ser objetos concretos porque ③ no tienen una ubicación en el espacio y ④ no interactúan causalmente con otros objetos. Por lo tanto, ⑤ los números son objetos abstractos.
La conclusión de este argumento es la última proposición, que los números son objetos abstractos. Observe que la primera premisa nos da una opción entre esta afirmación y una alternativa, que son concretas. La segunda premisa niega esa alternativa, por lo que las premisas 1 y 2 están trabajando juntas para apoyar la conclusión:
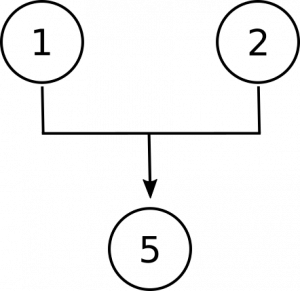
Ahora necesitamos hacer espacio en nuestro diagrama para las proposiciones 3 y 4. Están ahí para darnos razones para creer que los números no son objetos concretos. Primero, al afirmar que los números no se encuentran en el espacio como lo están los objetos concretos, y segundo afirmando que los números no interactúan con otros objetos, como lo hacen los objetos concretos. Estas son razones separadas e independientes para creer que no son concretas, así que terminamos con este diagrama:
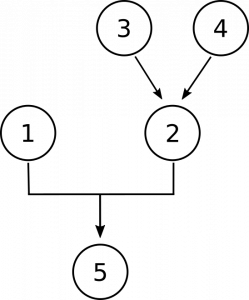
Lógica y Filosofía
En el corazón de la empresa lógica se encuentra una pregunta filosófica: ¿Qué hace un buen argumento? Es decir, ¿qué le corresponde a un conjunto de reclamos brindar apoyo a alguna otra reclamación? O tal vez: ¿Cuándo estamos justificados al hacer inferencias? Para responder a estas preguntas, los logísticos han desarrollado una amplia variedad de sistemas lógicos, cubriendo diferentes tipos de argumentos, y aplicando diferentes principios y técnicas. Muchas de las herramientas desarrolladas en la lógica se pueden aplicar más allá de los confines de la filosofía. El matemático que prueba un teorema, el informático programando una computadora, el lingüista modelando la estructura del lenguaje, todos ellos están usando métodos lógicos. Debido a que la lógica tiene una aplicación tan amplia, y debido a la sofisticación formal/matemática de muchos sistemas lógicos, ocupa un lugar único en el currículo filosófico. Una clase de lógica suele ser diferente a otras clases de filosofía en que se dedica muy poco tiempo directamente a interactuar e intentar responder a las “grandes preguntas”; más bien, uno se pone muy rápidamente en el negocio de aprender formalismos lógicos. Las preguntas que la lógica intenta responder son preguntas filosóficas importantes, pero las técnicas desarrolladas para responderlas son dignas de estudio por sí mismas.
Esto no significa, sin embargo, que debamos pensar en la lógica y la filosofía como meramente relacionadas tangencialmente; por el contrario, están profundamente entrelazadas. Para todas las campanas y silbatos formales que aparecen en el último sistema lógico de gama alta, en la parte inferior forma parte de un esfuerzo por responder a la pregunta fundamental de lo que se deduce de qué. Además, la lógica es útil para el filósofo practicante en al menos otras tres formas.
Los filósofos intentan responder preguntas profundas y molestas: sobre la naturaleza de la realidad, qué constituye una buena vida, cómo crear una sociedad justa, etc. Dan sus respuestas a estas preguntas, y respaldan esas respuestas con razones. Entonces otros filósofos consideran sus argumentos y responden con elaboraciones y críticas, argumentos propios. La filosofía se lleva a cabo y avanza a través del intercambio de argumentos. Ya que son la principal herramienta de su oficio, ¡es mejor que los filósofos sepan algo sobre lo que hace buenos argumentos! La lógica, por tanto, es esencial para la práctica de la filosofía.
Pero la lógica no es meramente una herramienta para evaluar argumentos filosóficos; ha alterado el curso de la conversación filosófica en curso. A medida que los logísticos desarrollaron sistemas formales para modelar la estructura de una gama cada vez más amplia de prácticas discursivas, los filósofos han podido aplicar sus conocimientos directamente a los problemas filosóficos tradicionales y reconocer vías de investigación previamente ocultas. Desde principios del siglo XX especialmente, la proliferación de enfoques novedosos en la lógica ha provocado una revolución en la práctica de la filosofía. No es demasiado exagerado decir que gran parte de la historia de la filosofía en el siglo XX constituía un intento continuo de enfrentar los nuevos desarrollos de la lógica, y el enfoque filosófico en el lenguaje que parecían exigir. Ningún tema filosófico —desde la metafísica hasta la ética y la epistemología y más allá— quedó intacto por esta revolución.
Por último, la lógica misma es fuente de fascinantes preguntas filosóficas. La pregunta básica en su esencia: ¿qué es para un reclamo seguir de los demás? —ramifica en innumerables direcciones, proporcionando un terreno fértil para la especulación filosófica. Hay lógica, y luego está la filosofía de la lógica. Se dice que la lógica es “formal”, por ejemplo. ¿Qué significa eso? Es una pregunta sorprendentemente difícil de responder. [5] Nuestras formulaciones lógicas más simples de oraciones condicionales (las que involucran “si”), conducen a aparentes paradojas. [6] ¿Cómo deben resolverse esos? ¿Deberían alterarse nuestros formalismos para captar mejor los significados del lenguaje natural de los condicionales? ¿Cuál es la relación adecuada entre los sistemas lógicos y los lenguajes naturales, de todos modos?
Tradicionalmente, la mayoría de los logísticos han aceptado que la lógica debe ser “bivalente”: toda proposición es verdadera o falsa. Pero los lenguajes naturales contienen términos vagos cuyos límites de aplicabilidad no siempre son claros. Por ejemplo, “calvo”: para ciertos sujetos, podríamos estar inclinados a decir que están bien en camino hacia la calvicie total, pero aún no del todo; por otro lado, estaríamos reacios a decir que no son calvos. Hay casos intermedios. Para tales casos, podríamos querer decir, por ejemplo, que la proposición de que Fredo es calvo no es ni verdadera ni falsa. Algunos logísticos han desarrollado lógicas que no son bivalentes, para hacer frente a este tipo de fenómeno lingüístico. Algunos agregan un tercer valor de verdad: “ninguno” o “indeterminado”, por ejemplo. Otros introducen infinitos grados de verdad (esto se llama “lógica difusa”). Estas lógicas se desvían de los enfoques tradicionales. ¿Por lo tanto, están equivocados en algún sentido? ¿O tienen razón, y los tradicionalistas están equivocados? ¿O incluso estamos haciendo una pregunta sensata cuando preguntamos si un sistema lógico en particular es correcto o incorrecto? ¿Podemos ser los llamados “pluralistas” lógicos, aceptando una variedad de lógicas incompatibles, dependiendo, por ejemplo, de si son útiles?
Este tipo de preguntas van más allá del alcance de este texto introductorio, por supuesto. Están incluidos para darte una idea de hasta dónde se puede llevar el estudio de la lógica. La tarea por ahora, sin embargo, es comenzar ese estudio.
EJERCIOS
En primer lugar, explique los siguientes argumentos, parafraseando lo necesario y sólo incluyendo premisas tácitas cuando se le instruya explícitamente para hacerlo. A continuación, diagrama de los argumentos.
- Los números, si existen, deben ser objetos concretos o abstractos. Los objetos concretos —como los planetas y las personas— son capaces de interactuar con otras cosas en las relaciones de causa y efecto. Los números carecen de esta habilidad. Por lo tanto, los números son objetos abstractos. [¡Necesitarás agregar una premisa intermedia implícita aquí! ]
- ¡Abolir la pena de muerte! ¿Por qué? Es inmoral. Numerosos estudios han demostrado que existe sesgo racial en su aplicación. El auge de las pruebas de ADN ha exonerado a decenas de presos condenados a muerte; ¿quién sabe cuántas personas inocentes han sido asesinadas en el pasado? La pena de muerte tampoco es práctica. La venganza es contraproducente: “Ojo por ojo deja ciego al mundo entero”, como dijo Gandhi. Además, los costos de litigar casos de pena de muerte, con sus interminables apelaciones, son enormes.
- Un sistema económico justo presentaría una distribución equitativa de los recursos y una ausencia de explotación. El capitalismo es un sistema económico injusto. Bajo el capitalismo, la distribución típica de la riqueza está muy sesgada a favor de los ricos. Y los trabajadores son explotados: a pesar de su papel esencial en la producción de bienes para el mercado, la mayor parte de las ganancias de las ventas de esos bienes van a los dueños de las empresas, no a sus trabajadores.
- La mente y el cerebro no son idénticos. ¿Cómo pueden ser idénticas las cosas si tienen propiedades diferentes? Hay una propiedad que la mente y el cerebro no comparten: el cerebro es divisible, pero la mente no lo es. Como todas las cosas materiales, el cerebro se puede dividir en partes—diferentes mitades, regiones, neuronas, etc. pero la mente es una unidad. Es mi esencia pensante, en la que no puedo discernir partes separadas. [7]
- Todo adulto sano debe participar en la fuerza laboral. Cuanta más gente trabaje, mayor será la riqueza de la nación, lo que beneficia a todos económicamente. Además, no hay reemplazo para la dignidad que los trabajadores encuentran en el trabajo. Por lo tanto, el gobierno debería emitir créditos fiscales para alentar a las personas a ingresar a la fuerza laboral. [Incluya en su explicación una premisa tácita, no expresada explícitamente en el pasaje, sino necesaria para sustentar la conclusión. ]
- Los símbolos que preceden a la conclusión, "
" representan la palabra “por lo tanto”.
- Esta no siempre es la razón. Algunas afirmaciones se dejan tácitas simplemente porque todo el mundo las acepta y declararlas explícitamente sería una pérdida de tiempo. Si argumentamos, “Los elefantes son mamíferos, y así de sangre caliente”, omitimos la afirmación de que todos los mamíferos son de sangre caliente por esta inocente razón.
- Estos argumentos incluso tienen un nombre especial: se les llama “teodicias”.
- Una versión extremadamente comprimida de las objeciones de Platón a la poesía en el Libro X de La República.
- John MacFarlane, en su disertación de doctorado ampliamente leída, gasta más de 300 páginas en esa cuestión. Ver: MacFarlane, J. 2000. “¿Qué significa decir que la lógica es formal?” Universidad de Pittsburgh.
- Para una explicación concisa, consulte la entrada de Wikipedia sobre paradojas de implicación material.
- Una versión simplificada de un argumento de Rene Descartes.


