12.1: OSCLADORES SINUSOIDALES
- Page ID
- 84125
Uno de los principales peligros que implica la aplicación de amplificadores operativos es que el usuario a menudo encuentra que oscilan en las conexiones que desea que fueran estables. Un objetivo de este libro es proporcionar orientación para ayudar a sortear este escollo común. Sin embargo, hay muchas aplicaciones que requieren una forma de onda periódica con frecuencia, forma de onda y amplitud controladas, y los amplificadores operativos se utilizan frecuentemente para generar estas señales.
Si se requiere una salida sinusoidal, las condiciones que deben cumplirse para generar esta forma de onda se pueden determinar a partir de la teoría de retroalimentación lineal presentada en capítulos anteriores.
Oscilador Wien-Bridge
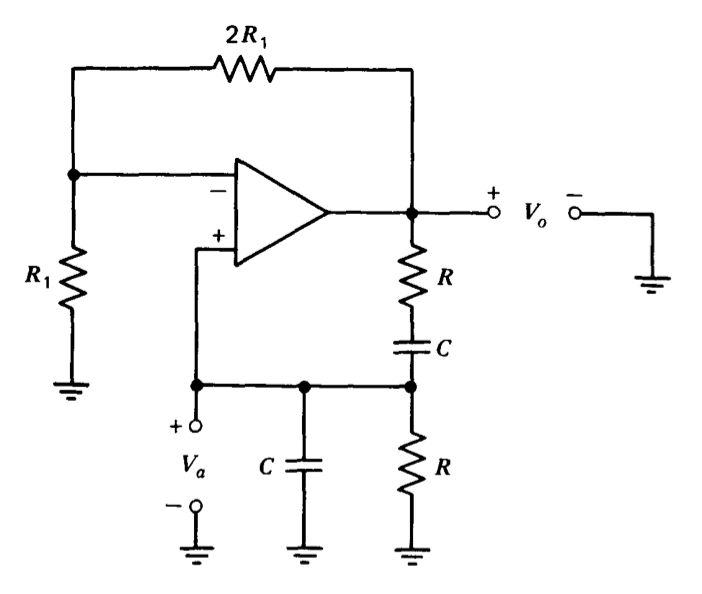
La corifiguración Wien-bridge (Figura 12.1) es una forma de implementar un oscilador sinusoidal. La función de transferencia de la red que conecta la salida del amplificador a su entrada no inversora es (en ausencia de carga)
\[\dfrac{V_a (s)}{V_o (s)} = \dfrac{RCs}{R^2 C^2 s^2 + 3RCs + 1} \label{eq12.1.1} \]
El amplificador operacional está conectado para una ganancia no inversora de 3. Combinando esta ganancia con\(\ref{eq12.1.1}\) rendimientos de ecuación para una transmisión de bucle en este sistema de retroalimentación positiva
\[L(s) = \dfrac{3RCs}{R^2 C^2 s^2 + 3RCs + 1} \nonumber \]
La ecuación característica
\[1 - L(s) = 1 - \dfrac{3RCs}{R^2 C^2 s^2 + 3RCs + 1} = \dfrac{R^2 C^2 s^2 + 1}{R^2 C^2 s^2 + 3RCs + 1} \label{eq12.1.3} \]
tiene ceros imaginarios en\(s = \pm (j/RC)\), y así el sistema puede sostener oscilaciones sinusoidales de amplitud constante a una frecuencia\(\omega = 1/RC\).
Osciladores en Cuadratura
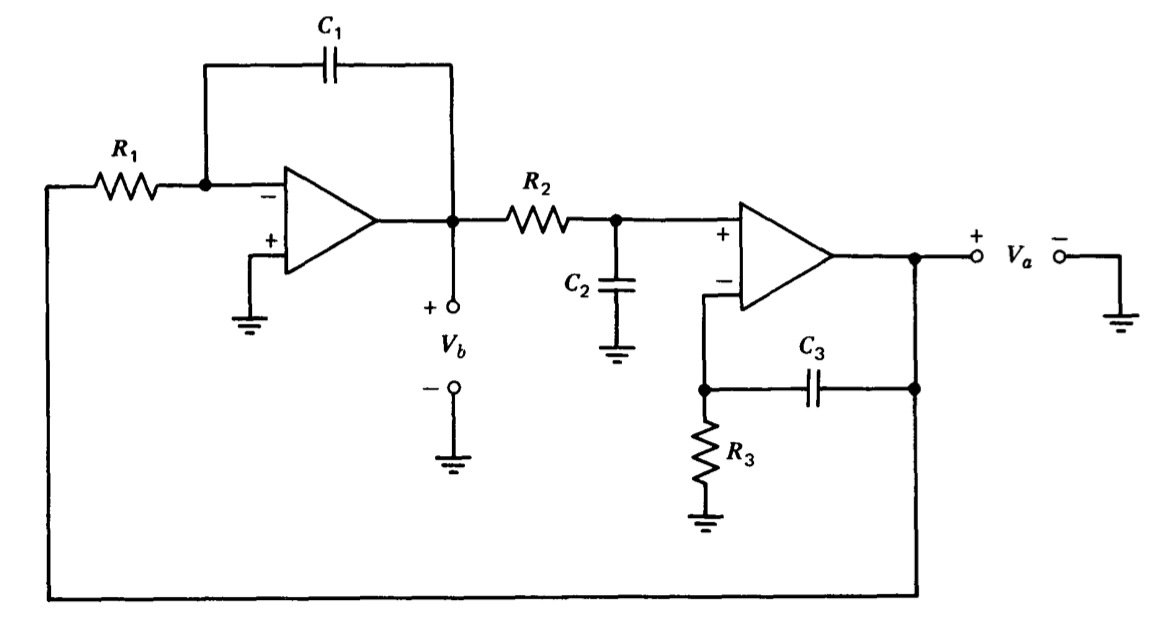
El oscilador en cuadratura (Figura 12.2) combina un integrador inversor y un integrador no inversor para proporcionar dos sinusoides desfasados en el tiempo uno\(90^{\circ}\) con respecto al otro. La transmisión en bucle para esta conexión es
\[L(s) = \left [-\dfrac{1}{R_1C_1s} \right ] \left [\dfrac{R_3C_3 s + 1}{(R_2C_2 s + 1) R_3C_3 s} \right ]\label{eq12.1.4} \]
En esta expresión, el primer término entre corchetes es la función de transferencia de bucle cerrado del amplificador operacional izquierdo (el integrador inversor), mientras que la segunda expresión entre corchetes es la función de transferencia de bucle cerrado del amplificador operacional derecho. Mediante la selección adecuada de los valores de los componentes, el amplificador derecho funciona como un integrador no inversor. De hecho, la discusión de esta conexión general en la Sección 11.4.1 muestra que solo se utiliza la entrada no inversora de una conexión diferencial como entrada de señal en esta aplicación.
Si las tres constantes de veces se hacen iguales de modo que\(R_1 C_1 = R_2 C_2 = R_3C_3 = RC\), Ecuación se\(\ref{eq12.1.4}\) reduce a
\[L(s) = -\dfrac{1}{R^2 C^2 s^2} \nonumber \]
La ecuación característica correspondiente para este sistema de retroalimentación negativa es
\[1 - L(s) = 1 + \dfrac{1}{R^2 C^2 s^2} = \dfrac{R^2 C^2 s^2 + 1}{R^2 C^2 s^2}\label{eq12.1.6} \]
Nuevamente, los ceros imaginarios de Ecuación\(\ref{eq12.1.6}\) indican el potencial de oscilación sinusoidal de amplitud constante. Tenga en cuenta que, dado que existe una integración entre\(V_a\) y\(V_b\), estas dos señales serán desfasadas en el tiempo por una\(90^{\circ}\) con respecto a la otra.
Un tipo similar de oscilador (sin una salida en cuadratura disponible) se puede construir usando un solo amplificador configurado como un integrador doble (Figura 11.12) con su salida conectada de nuevo a su entrada.
Estabilización de Amplitud por medio de Limitación
Existe una paradoja fundamental que complica el diseño de los osciladores sinusoidales. Una condición necesaria y suficiente para la generación de señales sinusoidales de amplitud constante es que un par de polos de bucle cerrado de un sistema de retroalimentación se encuentren en el eje imaginario y que no haya polos de bucle cerrado en la mitad derecha del\(s\) plano. Sin embargo, con esta condición exactamente satisfecha (una imposibilidad en cualquier sistema excepto puramente matemático), la amplitud de la salida del sistema viene determinada por las condiciones iniciales. En cualquier sistema físico, la desviación menor de la ubicación ideal del polo resulta en una oscilación con una amplitud exponencialmente creciente o en descomposición.
Es necesario incluir algún mecanismo en el oscilador para estabilizar su amplitud de salida al nivel deseado. Una posibilidad es diseñar el oscilador de manera que su par de polos dominantes se encuentre ligeramente a la derecha del eje imaginario para niveles de señal pequeños, y luego usar una no linealidad para limitar la amplitud a un nivel controlado. Este enfoque se ilustró en la Sección 6.3.3 como un ejemplo de análisis descriptivo de la función y se revisa brevemente aquí.
Considere el oscilador Wien-bridge que se muestra en la Figura 12.1. Si se cambia la relación de las resistencias que conectan la salida del amplificador a su entrada inversora, es posible cambiar la ganancia del amplificador de 3 a\(3(1 + \Delta )\). Como resultado, la ecuación\(\ref{eq12.1.3}\) se convierte en
\[1 - L(s) = 1 - \dfrac{3(1 + \Delta )}{R^2 C^2 s^2 + 3RCs + 1} = \dfrac{R^2C^2 s^2 - 3\Delta RCs + 1}{R^2C^2 s^2 + 3 RCs + 1} \nonumber \]
Los ceros de la ecuación característica (que son idénticamente las ubicaciones de los polos de bucle cerrado) se convierten en segundo orden con\(\omega_n = 1/RC\) y\(\zeta = - (3/2)\Delta\). En la práctica,\(\Delta\) se elige para que sea lo suficientemente grande como para que los polos de bucle cerrado permanezcan en el plano de la mitad derecha para todas las variaciones de parámetros anticipadas.
Por ejemplo, las tolerancias del valor de los componentes o la absorción dieléctrica asociadas con los condensadores alteran las ubicaciones de los polos de bucle cerrado.
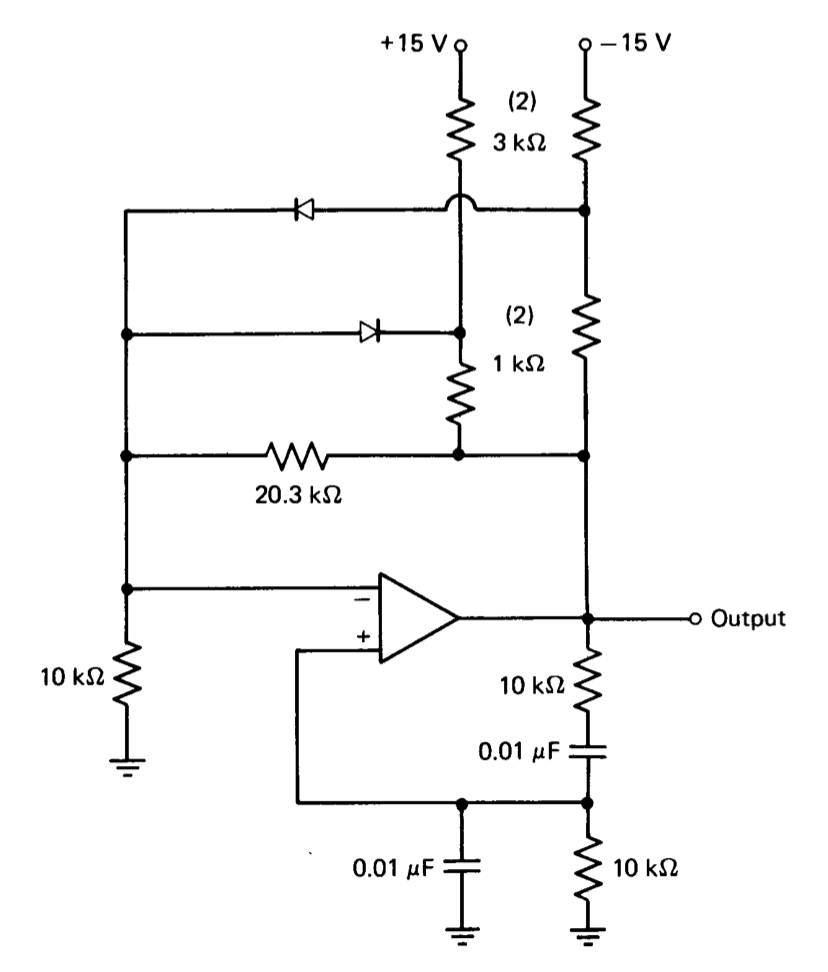
La limitación se puede usar entonces para disminuir el valor de\(\Delta\) (en un sentido de función de descripción) para que se controle la amplitud de salida. La Figura 12.3 muestra un circuito posible donde\(\Delta = 0.01\) se usa un valor de. La frecuencia de oscilación es\(10^4\) rad/seg o aproximadamente 1.6 kHz. La amplitud de salida es (lo que permite el voltaje directo del diodo) de aproximadamente 20 V pico a pico. Se utiliza la limitación simétrica ya que no agrega un componente d-c o incluso armónicos a la señal de salida si los diodos coinciden.
Control de amplitud por variación de parámetros
El uso de un limitador para cambiar un parámetro de bucle en un sentido de función de descripción después de que una amplitud de señal haya alcanzado un valor especificado es una forma de estabilizar la amplitud de salida de un oscilador. Este enfoque puede dar como resultado una distorsión armónica significativa de la señal de salida, particularmente cuando el oscilador está diseñado para funcionar a pesar de variaciones relativamente grandes en los valores de los elementos. Un enfoque alternativo, que a menudo resulta en una distorsión armónica significativamente menor, es usar un bucle de retroalimentación auxiliar para ajustar algún valor de parámetro de tal manera que coloque los polos de bucle cerrado precisamente en el eje imaginario, impidiendo nuevos cambios en la amplitud de la oscilación, una vez que se ha alcanzado el nivel deseado. Esta técnica es frecuentemente referida como control automático de ganancia, aunque en la práctica puede variar alguna cantidad distinta de ganancia.
Como ejemplo de este tipo de estabilización de amplitud, consideremos el efecto sobre el rendimiento de la resistencia variable\(R_3\) en el oscilador en cuadratura (Figura 12.2). Asumimos eso\(C_1 = C_2 = C_3\), y eso\(R_1 = R_2 = R\), mientras\(R_3 = (1 + \Delta ) R\). En este caso la transmisión en bucle del sistema (ver Ecuación\(\ref{eq12.1.4}\)) es con una ecuación característica correspondiente
\[1 - L(s) = \dfrac{R^3 C^3 (1 + \Delta) s^3 + R^2 C^2 (1 + \Delta) s^2 + RC(1 + \Delta) s + 1}{R^2 C^2 s^2 (1 + \Delta )(RCs + 1)} \nonumber \]
Si asumimos un pequeño valor para\(\Delta\), los ceros de la ecuación característica se pueden determinar fácilmente, ya que
\[\begin{array} {l} {R^3 C^3 (1 + \Delta) s^3 + R^2 C^2 (1 + \Delta) s^2 + RC (1 + \Delta ) s + 1} \\ {\left [RC \left (1 + \dfrac{\Delta}{2} \right ) s + 1 \right ] \left [R^2C^2 \left (1 + \dfrac{\Delta}{2} \right ) s^2 + RC \dfrac{\Delta}{2} s + 1 \right ] |\Delta | \ll 1} \end{array}\label{eq12.1.10} \]
El rendimiento del oscilador está, por supuesto, dominado por el par raíz complejo-conjugado indicado en la Ecuación\(\ref{eq12.1.10}\), y este par tiene una frecuencia natural\(\omega_n \simeq 1/RC\) y una relación de amortiguación\(\zeta \simeq A/4\). La característica importante es que los polos de bucle cerrado se pueden hacer para que se encuentren en la mitad izquierda o en la mitad derecha del plano s según el signo de\(\Delta\).
El diseño del bucle de amplitud-control para un oscilador en cuadratura proporciona un ejemplo interesante e instructivo de la manera en que las técnicas de retroalimentación desarrolladas en los Capítulos 2 a 6 pueden aplicarse a un circuito moderadamente complejo, y por esta razón investigaremos el problema con cierto detalle. Las dificultades se concentran principalmente en la fase de modelado del esfuerzo analítico.
Nuestra intención es enfocarnos en el control de amplitud, y este control se debe lograr moviendo los polos de bucle cerrado del oscilador hacia el plano izquierdo o derecho de acuerdo con si la amplitud de salida real es demasiado grande o demasiado pequeña, respectivamente. Suponemos que la señal\(v_A(t)\) (ver Figura 12.2) tiene la forma
\[v_A (t) = e_A (t) \sin \omega t \nonumber \]
Esta representación, que modela la señal como una sinusoide de frecuencia constante con una envolvente variable\(e_A(t)\), no es exacta, porque la frecuencia instantánea del componente sinusoidal de\(v_A\) es una función de\(\Delta\). Sin embargo, si el bucle de amplitud-control tiene una frecuencia de cruce muy baja en comparación con la frecuencia de oscilación para que los cambios de magnitud sean relativamente lentos, podemos considerar la amplitud\(e_A\) sola e ignorar la porción sinusoidal de la expresión. En este caso la frecuencia exacta de la sinusoide no es importante.
Para encontrar la dependencia del parámetro de\(v_A\) control\(\Delta\), supongamos que el circuito está oscilando con\(\Delta = 0\) lo que los polos de bucle cerrado del oscilador están precisamente en el eje imaginario. Con esta restricción la envolvente es constante con algún valor de punto operativo de\(E_A\) modo que
\[v_A (t) = E_A \sin \omega t \nonumber \]
donde\(\omega = 1/RC\). Si\(\Delta\) experimenta un cambio gradual gradual a un nuevo valor\(\Delta_1\) en el momento\(t = 0\), los polos del oscilador se mueven hacia el plano de la mitad izquierda (para positivo\(\Delta_1\)), y
\[v_A (t) \simeq E_A e^{-\zeta \omega_n t} \sin \omega_n t \label{eq12.1.13} \]
Insertar valores para\(\zeta\) y\(\omega_n\) desde Ecuación\(\ref{eq12.1.10}\) en\(\ref{eq12.1.13}\) Rendimientos de Ecuación
\[v_A (t) \simeq E_A e^{-(\Delta_1 t/4RC)} \sin \dfrac{t}{RC} \nonumber \]
La envolvente para esta señal es
\[e_A (t) = E_A e^{-(\Delta_1 t/4RC)} = E_A \left [ 1 - \dfrac{\Delta_1 t}{4RC} + \dfrac{1}{2} \left (\dfrac{\Delta_1 t}{4RC} \right )^2 - \cdots + \right ] \nonumber \]
Si\(\Delta_1 t/4RC\) es pequeño (una condición asegurada por un valor suficientemente pequeño de\(\Delta_1\)), podemos separarlos\(e_A(t)\) en componentes de punto operativo e incrementales como
\[e_A (t) = E_A + e_a (t) \simeq E_A - \dfrac{E_A \Delta_1}{4RC} t \nonumber \]
Por lo tanto, un cambio gradual positivo\(\Delta\) conduce a un cambio incremental de envolvente que es una función lineal decreciente del tiempo. Esta condición implica que la función de transferencia linealizada que relaciona la amplitud de la envolvente\(\Delta\) es
\[\dfrac{E_a (s)}{\Delta (s)} = - \dfrac{E_A}{4RCs} \label{eq12.1.17} \]
Este análisis linealizado confirma la sensación de que el control del valor de\(\Delta\) es de hecho una forma razonable de estabilizar la amplitud de la oscilación, ya que el cambio incremental en la envolvente de la oscilación es proporcional a la integral de tiempo de\(\Delta\).
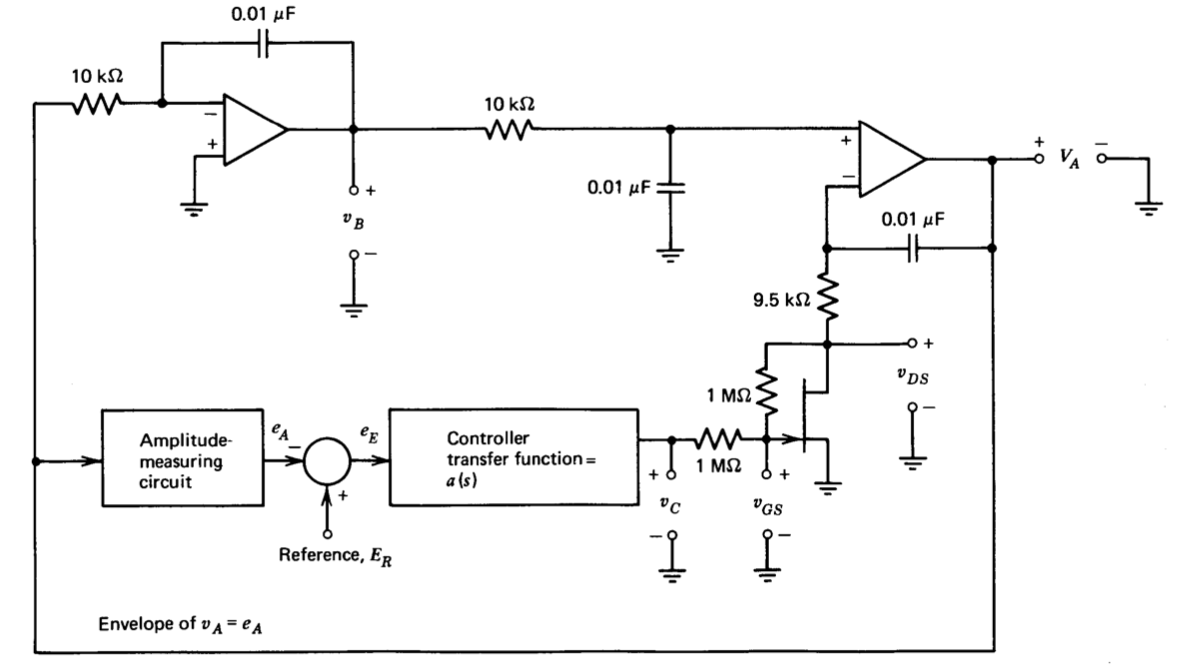
El diseño adicional del bucle de amplitud-control depende de la topología real del sistema. La Figura 12.4 muestra una posible implementación en forma de circuito mixto y diagrama de bloques funcional. La envolvente de la señal a controlar está determinada por un circuito de medición de amplitud. Este circuito puede ser un simple detector de pico de diodo-resistor-condensador en los casos en que no se requiere alta precisión, o puede ser un tipo de conexión activa de “superdiodo” (un ejemplo se da en la Sección 12.5.1) en más
aplicaciones exigentes. En cualquier caso, el diseño de este circuito no es particularmente difícil y no se discutirá aquí. La envolvente de la señal se compara con un valor de referencia, y la señal de error resultante pasa a través de un controlador lineal con una función de transferencia\(a(s)\). La salida del controlador se utiliza para accionar un transistor de efecto de campo que funciona como una resistencia variable cuyo valor determina\(\Delta\).
La conexión FET incorpora compensación local para linealizar sus características como se muestra en el siguiente desarrollo. Si un FET de unión está polarizado en conducción con un pequeño voltaje aplicado a través de su canal, y su puerta polarizada inversa con respecto a su canal, la corriente de drenaje está aproximadamente relacionada con tensiones terminales como
\[i_D = K \left [(v_{GS} + V_P) v_{DS} - \dfrac{v_{DS}^2}{2} \right ] \label{eq12.1.18} \]
donde\(K\) es una constante dependiente de la construcción del transistor, y\(V_P\) es la magnitud del voltaje de pinch-off de puerta a fuente.
La\(i_D\) dependencia del cuadrado de la tensión drenaje-fuente es indeseable, ya que este término representa una no linealidad en la resistencia del canal del dispositivo, y esta no linealidad introducirá distorsión armónica en la salida del oscilador. La no linealidad se puede eliminar agregando la mitad del voltaje de drenaje a fuente al voltaje de puerta a fuente a través de resistencias como se muestra en la Figura 12.4. Las resistencias son lo suficientemente grandes como para que no deriven significativamente la resistencia drenaje-fuente del FET en condiciones normales de operación. Con la topología mostrada,
\[v_{GS} = \dfrac{1}{2} (v_C + v_{DS}) \label{eq12.1.19} \]
Sustituir la ecuación\(\ref{eq12.1.19}\) en ecuación\(\ref{eq12.1.18}\) muestra que
\[i_D = K\left [\left (\dfrac{v_C}{2} + \dfrac{v_{DS}}{2} + V_P \right ) v_{DS} - \dfrac{v_{DS}^2}{2} \right ] = K \left (\dfrac{v_C}{2} + V_P \right ) v_{DS} \nonumber \]
o
\[R_{DS} = \dfrac{\partial v_{DS}}{\partial i_D} = \dfrac{1}{K[(v_C/2) + V_P]}\label{eq12.1.21} \]
Esta ecuación indica que la resistencia incremental del FET es independiente de la tensión drenaje-fuente cuando se incluye la red.
Para fines de diseño, asumimos que el FET se caracteriza por\(V_P = 4\) voltios y\(K = 10^{-3}\) mho por voltio. Recordemos que las oscilaciones de amplitud estable requieren que las tres constantes de\(R-C\) tiempo sean idénticas; por lo tanto, el valor del punto operativo de\(R_{DS}\) es de 500 ohmios. La ecuación\(\ref{eq12.1.21}\) combinada con parámetros FET indica que este valor resulta con un valor de punto operativo para el voltaje de control de -4 voltios. El cambio incremental en\(R_{DS}\) función del voltaje de control en este punto de operación, obtenido diferenciando\(\ref{eq12.1.21}\) con respecto a\(v_C\),
\[\dfrac{\partial R_{DS}}{\partial v_C}|_{v_C = -4V} = -125 \Omega /V \label{eq12.1.22} \]
El modelado anterior se realizó en términos de\(\Delta\), la desviación fraccionaria de la resistencia\(R_3\) en la Figura 12.2 de su valor nominal. Esta resistencia consiste en el FET más una\(9.5\ k\Omega\) resistencia en la implementación real. La dependencia incremental de\(\Delta\) la tensión de control se determina dividiendo la ecuación\(\ref{eq12.1.22}\) por el valor de punto operativo anticipado de la resistencia total,\(10\ k\Omega\). Así
\[\dfrac{\partial \Delta}{\partial v_C}|_{v_C = -4V} = -0.0125 V^{-1} \label{eq12.1.23} \]
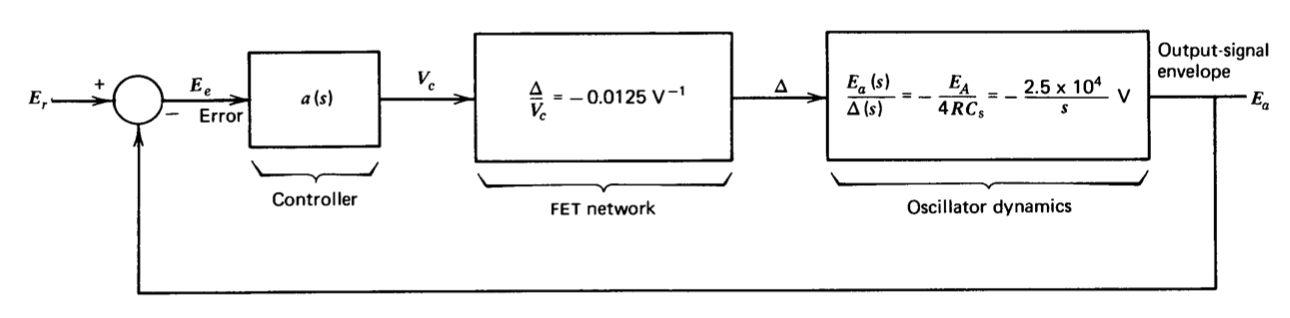
Las relaciones resumidas en Ecuaciones\(\ref{eq12.1.17}\) y\(\ref{eq12.1.23}\) combinadas con la topología del sistema y un supuesto valor de punto operativo para los\(E_A = 10\) voltios envolventes conducen al diagrama de bloques linealizado para el bucle amplitud-contrrol mostrado en la Figura 12.5. El negativo de la transmisión en bucle para este sistema es
\[\dfrac{E_a (s)}{E_e (s)} = a(s) \times \dfrac{312.5}{s} \nonumber \]
Una serie de factores rigen la elección de\(a(s)\) para esta aplicación, incluyendo:
(a) El voltaje real de puerta a fuente del FET requerido en condiciones de reposo depende en gran medida de los parámetros FET y de los valores exactos de los demás componentes utilizados en el circuito. La manera más fácil de asegurar que la diferencia entre la envolvente y la referencia sea constante a pesar de estos parámetros variables es incluir una integración\(a(s)\) ya que esta integración fuerza el valor del punto operativo del error a cero.
(b) El análisis se basa en una frecuencia de cruce mucho menor para el bucle de amplitud-control que la frecuencia de oscilación,\(10^4\) radianes por segundo. Sin embargo, un bucle de control de muy baja frecuencia acentúa el efecto sobre la amplitud de cambios rápidos en cantidades como los voltajes de suministro. Un compromiso algo arbitrario es elegir una frecuencia de cruce de 100 radianes por segundo.
(c) Dado que el análisis se basa en una jerarquía de aproximaciones, el sistema debe diseñarse para tener un margen de fase muy conservador.
(d) La función de transferencia del controlador debe incluir filtrado paso bajo. La señal del detector que indica la amplitud de la envolvente incluye invariablemente componentes en la frecuencia de oscilación o sus armónicos. Si estos componentes no se filtran de manera que estén en un nivel insignificante cuando se aplican a la puerta FET, la modulación de resistencia de canal resultante introduce distorsión en la señal de salida del oscilador.
Una función de transferencia de controlador que incorpora estas características es
\[a(s) = \dfrac{3.2 (0.1s + 1)}{s(10^{-3} s + 1)^2} \nonumber \]
El negativo de la transmisión en bucle con este valor para\(a(s)\) es
\[\dfrac{E_a (s)}{E_e (s)} = \dfrac{}{} \nonumber \]
La frecuencia de cruce del sistema es de 100 radianes por segundo, y el margen de fase supera\(70^{\circ}\) con este valor para\(a(s)\).
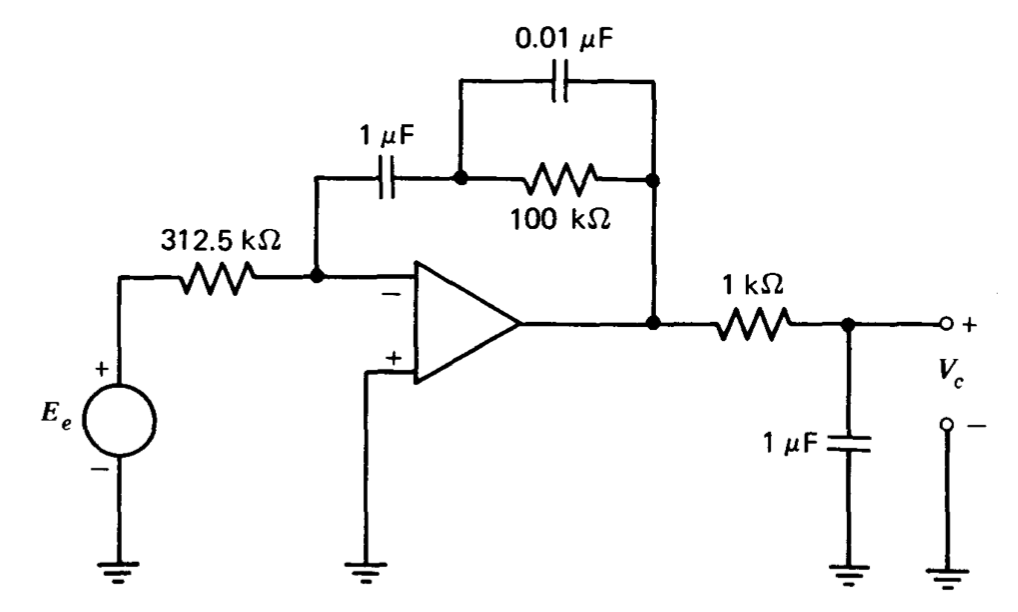
Un posible circuito que proporciona el negativo de lo deseado\(a(s)\) se muestra en la Figura 12.6. En muchos casos de interés práctico, esta inversión puede ser confirmada por algún reordenamiento del circuito de medición de amplitud. El segundo polo filtrante requerido se obtiene con una red pasiva. El nivel de impedancia de la red del filtro es lo suficientemente bajo para que la red no se vea perturbada por la\(2-M\Omega\) carga conectada a ella.
El nivel de referencia requerido para establecer la amplitud del oscilador se puede aplicar al controlador agregando otra resistencia de entrada al amplificador operacional. También puede ser posible realizar parte de la circuitería de medición de amplitud con este amplificador. Un ejemplo de este tipo de combinación de funciones se da en la Sección 12.5.1.
Dos consideraciones prácticas involucradas en el diseño de este oscilador merecen una mención especial. Primero, la señal\(v_B\) normalmente tiene menor distorsión armónica que la que tiene\(v_A\) ya que la integración del primer amplificador filtra cualquier armónico que pueda ser introducido por el FET. Segundo, es posible variar la amplitud de referencia para este circuito y así modular la amplitud de la salida del oscilador. Sin embargo, el ancho de banda de control en este modo será relativamente pequeño, y el rendimiento cambiará en función de la amplitud de la envolvente en reposo ya que la magnitud de la transmisión de bucle depende de los niveles operativos.
El rendimiento de un oscilador de este tipo puede ser bastante impresionante. El control de amplitud dentro de\(1\ mV\) pico a pico es posible si se utilizan “superdiodos” en el detector de envolvente. La distorsión armónica de la señal de salida se puede mantener un factor de\(10^4\) o más por debajo del componente fundamental.