1.3: Comunicación a distancia
- Page ID
- 83299
La comunicación mediante señales EM ha sido una parte integral de la sociedad desde la transmisión de las primeras señales telegráficas a través de cables a mediados del siglo XIX [7]. Este desarrollo derivó de una comprensión de la inducción magnética basada en los experimentos de Faraday en 1831 [8] en los que investigó la relación de los campos magnéticos y las corrientes. Esta obra de Faraday ahora se conoce como la ley de Faraday, o la ley de inducción de Faraday. Fue una de las cuatro leyes clave desarrolladas entre 1820 y 1835 que describieron la interacción de los campos estáticos y de los campos estáticos con las corrientes. Estos cuatro
| Banda | Rango de frecuencia |
|---|---|
| \(\text{L}\)“largo” | \(1-2\text{ GHz}\) |
| \(\text{S}\)“corto” | \(2-4\text{ GHz}\) |
| \(\text{C}\)“compromiso” | \(4-8\text{ GHz}\) |
| \(\text{X}\)“extendido” | \(8-12\text{ GHz}\) |
| \(\text{K}_{u}\)“kurtz bajo” | \(12-18\text{ GHz}\) |
| \(\text{K}\)“kurtz” (corto en alemán) | \(18-27\text{ GHz}\) |
| \(\text{K}_{a}\)“kurtz arriba” | \(27-40\text{ GHz}\) |
| \(\text{V}\) | \(40-75\text{ GHz}\) |
| \(\text{W}\) | \(75-110\text{ GHz}\) |
| \(\text{F}\) | \(90-140\text{ GHz}\) |
| \(\text{D}\) | \(110-170\text{ GHz}\) |
| \(\text{mm}\) | \(110-300\text{ GHz}\) |
Tabla\(\PageIndex{1}\): Bandas de radar IEEE [6]. La designación de banda mm también se usa cuando la intención es transmitir la información general anterior\(30\text{ GHz}\).
Nota
En\(\PageIndex{2}\) la Tabla las dimensiones de la guía de ondas se especifican en pulgadas (\(25.4\text{ mm/inch}\)se usa para convertir a\(\text{mm}\)). El número en la designación WR es la dimensión interna larga de la guía de ondas en centésimas de pulgada. La EIA es la Asociación de la Industria Electrónica con sede en Estados Unidos. Tenga en cuenta que la banda de radar (ver Tabla\(\PageIndex{1}\)) y las designaciones de banda de guía de ondas no necesariamente coinciden.
| Banda | Banda de guía de ondas EIA | Frecuencia de funcionamiento (\(\text{GHz}\)) | Dimensiones internas (\(a\times b\), pulgadas) |
|---|---|---|---|
| \(\text{R}\) | WR-430 | \ (\ text {GHz}\)) ">\(1.70-2.60\) | \ (a\ veces b\), pulgadas) ">\(4.300\times 2.150\) |
| \(\text{D}\) | WR-340 | \ (\ text {GHz}\)) ">\(2.20-3.30\) | \ (a\ veces b\), pulgadas) ">\(3.400\times 1.700\) |
| \(\text{S}\) | WR-284 | \ (\ text {GHz}\)) ">\(2.60-3.95\) | \ (a\ veces b\), pulgadas) ">\(2.840\times 1.340\) |
| \(\text{E}\) | WR-229 | \ (\ text {GHz}\)) ">\(3.30-4.90\) | \ (a\ veces b\), pulgadas) ">\(2.290\times 1.150\) |
| \(\text{G}\) | WR-187 | \ (\ text {GHz}\)) ">\(3.95-5.85\) | \ (a\ veces b\), pulgadas) ">\(1.872\times 0.872\) |
| \(\text{F}\) | WR-159 | \ (\ text {GHz}\)) ">\(4.90-7.05\) | \ (a\ veces b\), pulgadas) ">\(1.590\times 0.795\) |
| \(\text{C}\) | WR-137 | \ (\ text {GHz}\)) ">\(5.85-8.20\) | \ (a\ veces b\), pulgadas) ">\(1.372\times 0.622\) |
| \(\text{H}\) | WR-112 | \ (\ text {GHz}\)) ">\(7.05-10.00\) | \ (a\ veces b\), pulgadas) ">\(1.122\times 0.497\) |
| \(\text{X}\) | WR-90 | \ (\ text {GHz}\)) ">\(8.2-12.4\) | \ (a\ veces b\), pulgadas) ">\(0.900\times 0.400\) |
| \(\text{Ku}\) | WR-62 | \ (\ text {GHz}\)) ">\(12.4-18.0\) | \ (a\ veces b\), pulgadas) ">\(0.622\times 0.311\) |
| \(\text{K}\) | WR-51 | \ (\ text {GHz}\)) ">\(15.0-22.0\) | \ (a\ veces b\), pulgadas) ">\(0.510\times 0.255\) |
| \(\text{K}\) | WR-42 | \ (\ text {GHz}\)) ">\(18.0-26.5\) | \ (a\ veces b\), pulgadas) ">\(0.420\times 0.170\) |
| \(\text{Ka}\) | WR-28 | \ (\ text {GHz}\)) ">\(26.5-40.0\) | \ (a\ veces b\), pulgadas) ">\(0.280\times 0.140\) |
| \(\text{Q}\) | WR-22 | \ (\ text {GHz}\)) ">\(33-50\) | \ (a\ veces b\), pulgadas) ">\(0.224\times 0.112\) |
| \(\text{U}\) | WR-19 | \ (\ text {GHz}\)) ">\(40-60\) | \ (a\ veces b\), pulgadas) ">\(0.188\times 0.094\) |
| \(\text{V}\) | WR-15 | \ (\ text {GHz}\)) ">\(50-75\) | \ (a\ veces b\), pulgadas) ">\(0.148\times 0.074\) |
| \(\text{E}\) | WR-12 | \ (\ text {GHz}\)) ">\(60-90\) | \ (a\ veces b\), pulgadas) ">\(0.122\times 0.061\) |
| \(\text{W}\) | WR-10 | \ (\ text {GHz}\)) ">\(75-110\) | \ (a\ veces b\), pulgadas) ">\(0.100\times 0.050\) |
| \(\text{F}\) | WR-8 | \ (\ text {GHz}\)) ">\(90-140\) | \ (a\ veces b\), pulgadas) ">\(0.080\times 0.040\) |
| \(\text{D}\) | WR-6 | \ (\ text {GHz}\)) ">\(110-170\) | \ (a\ veces b\), pulgadas) ">\(0.0650\times 0.0325\) |
| \(\text{G}\) | WR-5 | \ (\ text {GHz}\)) ">\(140-220\) | \ (a\ veces b\), pulgadas) ">\(0.0510\times 0.0255\) |
Tabla\(\PageIndex{2}\): Bandas de guía de ondas seleccionadas con frecuencias de funcionamiento y dimensiones internas (consulte la Figura 1.2.2).
son la ley Biot-Savart (desarrollada alrededor de 1820), la ley de Ampere (1826), la ley de Faraday (1831) y la ley de Gauss (1835). Todas estas son leyes estáticas y no describen campos propagantes.
1.3.1 Campos electromagnéticos
Ahora sabemos que hay dos componentes del campo EM, el campo eléctrico,\(E\), con unidades de voltios por metro (\(\text{V/m}\)), y el campo magnético,\(H\), con unidades de amperios por metro (\(\text{A/m}\)). \(E\)y\(H\) campos juntos describen la fuerza entre cargos. También hay dos cantidades de flujo que son necesarias para entender las interacciones entre estos campos y el vacío o la materia. El primero es\(D\), la densidad de flujo eléctrico, con unidades de culombios por metro cuadrado (\(\text{C/m}^{2}\)), y el otro es\(B\), la densidad de flujo magnético, con unidades de teslas (\(\text{T}\)). \(B\)y\(H\), y\(D\) y\(E\), se relacionan entre sí por las propiedades del medio, que se plasman en las cantidades\(\mu\) y\(\varepsilon\) (con la letra caligráfica, por ejemplo\(\mathcal{B}\), denotando una cantidad en el dominio del tiempo):
\[\label{eq:1}\overline{\mathcal{B}}=\mu\overline{\mathcal{H}} \]
\[\label{eq:2}\overline{\mathcal{D}}=\varepsilon\overline{\mathcal{E}} \]
donde la barra superior denota una cantidad vectorial, y\(\mu\) se llama permeabilidad del medio y describe la capacidad de almacenar energía magnética en una región. Se denota la permeabilidad en el espacio libre (o vacío)\(\mu_{0}=4\pi\times 10^{-7}\text{ H/m}\) y el flujo magnético y el campo magnético se relacionan como
\[\label{eq:3}\overline{\mathcal{B}}=\mu_{0}\overline{\mathcal{H}} \]
La otra cantidad de material es la permitividad\(\varepsilon\), que describe la capacidad de almacenar energía en un volumen y en un vacío
\[\label{eq:4}\overline{\mathcal{D}}=\varepsilon_{0}\overline{\mathcal{E}} \]
donde\(\varepsilon_{0} = 8.854\times 10^{-12}\text{ F/m}\) está la permitividad de un vacío. La permitividad relativa,\(\varepsilon_{r}\), es la relación entre la permitividad de un material y la del vacío:
\[\label{eq:5}\varepsilon_{r}=\varepsilon /\varepsilon_{0} \]
De igual manera, la permeabilidad relativa\(\mu_{r}\), se refiere a la relación de permeabilidad de un material a su valor en vacío:
\[\label{eq:6}\mu_{r}=\mu /\mu_{0} \]
1.3.2 Ley Biot-Savart
La ley Biot-Savart relaciona la corriente con el campo magnético como, ver Figura\(\PageIndex{1}\),
\[\label{eq:7}d\overline{H} = \frac{Id\ell\times\hat{a}_{R}}{4\pi R^{2}} \]
que tiene las unidades de amperios por metro en el sistema SI. En Ecuación\(\eqref{eq:7}\)\(d\overline{H}\) está el\(H\) campo estático incremental,\(I\) es actual,\(d\ell\) es el vector de la longitud de un filamento de corriente\(I\),\(\hat{a}_{R}\) es el vector unitario en la dirección del filamento actual al campo magnético, y\(R\) es la distancia entre el filamento y el campo magnético. El\(d\overline{H}\) campo se dirige en ángulo recto hacia\(\hat{a}_{R}\) y el filamento actual. Entonces Ecuación\(\eqref{eq:7}\) dice que un filamento de corriente produce un campo magnético en un punto. El campo magnético total de una corriente en un alambre o superficie se puede encontrar modelando el alambre o superficie como una serie de filamentos de corriente, y el campo magnético total en un punto se obtiene integrando las contribuciones de cada filamento.
1.3.3 Ley de Inducción de Faraday
La ley de Faraday relaciona un campo magnético variable en el tiempo con una caída de voltaje inducida\(V\), alrededor de un camino cerrado, que ahora se entiende como\(\oint_{\ell}\overline{\mathcal{E}}\cdot d\ell\), es decir, el contorno cerrado integral del campo eléctrico,
\[\label{eq:8}V=\oint_{\ell}\overline{\mathcal{E}}\cdot d\ell = -\oint_{s}\frac{\partial\overline{\mathcal{B}}}{\partial t}\cdot d\text{s} \]
y esto tiene las unidades de voltios en el sistema de unidades SI. La operación descrita en la Ecuación\(\eqref{eq:8}\) se ilustra en la Figura\(\PageIndex{2}\).
1.3.4 Ley Circuital de Ampere
La ley circuital de Ampere, a menudo llamada solo ley de Ampere, relaciona la corriente continua y el campo magnético estático\(\overline{\mathcal{H}}\). La relación se basa en la figura\(\PageIndex{3}\) y la ley circuital de Ampere es
\[\label{eq:9}\oint_{\ell}\overline{H}\cdot d\ell = I_{\text{enclosed}} \]
Es decir, la integral del campo magnético alrededor de un bucle es igual a la corriente encerrada por el bucle. Usando simetría, la magnitud del campo magnético a una\(r\) distancia del centro del cable que se muestra en la Figura\(\PageIndex{3}\) es
\[\label{eq:10}H=|I|/(2\pi r) \]
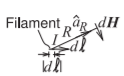
Figura\(\PageIndex{1}\): Diagrama que ilustra la ley Biot-Savart. La ley relaciona un filamento estático de corriente con el\(H\) campo incremental a distancia.
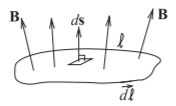
Figura\(\PageIndex{2}\): Diagrama que ilustra la ley de Faraday. El contorno\(\ell\) encierra la superficie.
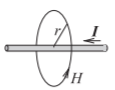
Figura\(\PageIndex{3}\): Diagrama que ilustra la ley de Ampere. La ley de Ampere relaciona la corriente,\(I\), en un cable con el campo magnético que lo rodea,\(H\).
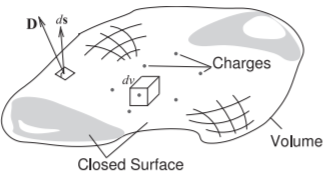
Figura\(\PageIndex{4}\): Diagrama que ilustra la ley de Gauss. Las cargas se distribuyen en el volumen encerrado por la superficie cerrada. Un área incremental es descrita por el vector\(d\mathbf{S}\), que es normal a la superficie y cuya magnitud es el área del área incremental.
1.3.5 Ley de Gauss
La ley final de EM estática es la ley de Gauss, que relaciona el vector de densidad de flujo eléctrico estático,\(\overline{\mathcal{D}}\), con la carga. Con referencia a la Figura\(\PageIndex{4}\), la ley de Gauss en forma integral es
\[\label{eq:11}\oint_{s}\overline{D}\cdot d\text{s}=\int_{v}\rho_{v}\cdot dv=Q_{\text{enclosed}} \]
Esto establece que la integral del vector de flujo eléctrico,\(\overline{D}\), sobre una superficie cerrada es igual a la carga total encerrada por la superficie,\(Q_{\text{enclosed}}\).
1.3.6 Ley del Magnetismo de Gauss
La ley del magnetismo de Gauss es paralela a la ley de Gauss que ahora se aplica a los campos magnéticos. En forma integral la ley es
\[\label{eq:12}\oint_{s}\overline{B}\cdot d\text{s}=0 \]
Esto establece que la integral del vector de flujo magnético,\(\overline{D}\), sobre una superficie cerrada es cero reflejando el hecho de que no existen cargas magnéticas.
1.3.7 Telégrafo
Con las leyes de campo estático establecidas, se estableció el escenario para iniciar el desarrollo de la transmisión de señales EM a través de cables. Mientras viajaba en barco de regreso a Estados Unidos desde Europa en 1832, Samuel Morse se enteró de los experimentos de Faraday y concibió un telégrafo EM. Buscó socios en Leonard Gale, profesor de ciencias en la Universidad de Nueva York, y Alfred Vail, “experto en las artes mecánicas”, quienes construyeron los modelos telegráficos utilizados en sus experimentos. En 1835 esta colaboración llevó a una versión experimental que transmitía una señal sobre\(16\text{ km}\) cable. Morse no era
| Símbolo | Código |
|---|---|
| \(1\) | . — |
| \(2\) | .. — |
| \(3\) | ... — |
| \(4\) | ... - |
| \(5\) | ... |
| \(6\) | -... |
| \(7\) | —... |
| \(8\) | —.. |
| \(9\) | —. |
| \(0\) | — |
| \(\text{A}\) | . - |
| \(\text{B}\) | -... |
| \(\text{C}\) | -.-. |
| \(\text{D}\) | -.. |
| \(\text{E}\) | . |
| \(\text{F}\) | .. -. |
| \(\text{G}\) | —. |
| \(\text{H}\) | ... |
| \(\text{I}\) | . |
| \(\text{J}\) | . — |
| \(\text{K}\) | -.- |
| \(\text{L}\) | .-.. |
| \(\text{M}\) | - - |
| \(\text{N}\) | -. |
| \(\text{O}\) | — |
| \(\text{P}\) | .—. |
| \(\text{Q}\) | — .- |
| \(\text{R}\) | .-. |
| \(\text{S}\) | ... |
| \(\text{T}\) | - |
| \(\text{U}\) | .. - |
| \(\text{V}\) | ... - |
| \(\text{W}\) | . — |
| \(\text{X}\) | - .. - |
| \(\text{Y}\) | - . — |
| \(\text{Z}\) | —.. |
Tabla\(\PageIndex{3}\): Código Morse Internacional.
solo en imaginar un telégrafo EM, y en 1837 Charles Wheatstone abrió la primera línea de telégrafo comercial entre Londres y Camden Town, Inglaterra, a una distancia de\(2.4\text{ km}\). Posteriormente, en 1844, Morse diseñó y desarrolló una línea para conectar Washington, DC y Baltimore, Maryland. Esto culminó con la primera transmisión pública el 24 de mayo de 1844, cuando Morse envió un mensaje telegráfico desde el Capitolio de Washington a Baltimore. Este evento es reconocido como el nacimiento de la comunicación a distancia mediante cables. Este rápido ritmo de transición de la investigación básica al electromagnetismo (experimento de Faraday) a un sistema de transmisión de campo se ha repetido muchas veces en la evolución de la tecnología de comunicación cableada e inalámbrica.
Los primeros sistemas telegráficos utilizaban baterías de inducción EM y multicelulares que se conectaban y desconectaban del circuito con el cable telegráfico largo y así creaban pulsos de corriente. Ahora sabemos que estos pulsos de corriente crearon campos magnéticos propagadores que fueron guiados por los cables y fueron acompañados por campos eléctricos. En 1840 Morse solicitó una patente estadounidense para “Mejora en el modo de comunicación de información mediante señales mediante la aplicación del telégrafo de electromagnetismo”, que describía “cables de rayos” y “código Morse”. Para 1854,\(37,000\text{ km}\) de alambre telegráfico cruzó Estados Unidos, y esto tuvo un profundo efecto en el desarrollo del país. Los ferrocarriles hicieron temprano un uso extensivo del telégrafo y se creó una nueva industria. En Estados Unidos la industria del telégrafo estuvo dominada por Western Union, que se convirtió en una de las empresas más grandes del mundo. Al igual que con el telégrafo, la historia de la comunicación por cable e inalámbrica ha sido moldeada tanto por la política, los intereses comerciales, el riesgo de mercado, el emprendimiento, la propiedad de patentes y los litigios de patentes como por la propia tecnología.
Las primeras señales telegráficas fueron solo ráfagas cortas y ráfagas de ruido ligeramente más largas usando código Morse en el que secuencias de puntos, guiones y pausas representan números y letras (ver Tabla\(\PageIndex{3}\)). \(^{1}\)La velocidad de transmisión fue determinada por la capacidad del operador para teclear y reconocer los códigos. La transferencia de información usando señales EM a finales del siglo XIX fue por lo tanto aproximadamente\(5\) bits por segundo (bits/s). Morse logró\(10\) palabras por minuto.
1.3.8 Los orígenes de la radio
En la década de 1850 Morse comenzó a experimentar con la transmisión inalámbrica, pero esto aún se basaba en el principio de conducción. Utilizó un río que fluye, que como se conoce ahora es un medio rico en iones, para llevar la carga. A un lado del río instaló una conexión en serie de una placa metálica, una batería, una llave Morse y una segunda placa metálica. Esto formó el circuito transmisor. Las placas metálicas se insertaron en el agua y se separaron por una distancia considerablemente mayor que la anchura del río. Al otro lado del río, se colocaron placas metálicas directamente opuestas a las placas transmisoras y este segundo conjunto de placas se conectó por un cable a un galvanómetro en serie. Esto formó el circuito de recepción, y los pulsos eléctricos establecidos por el transmisor dieron como resultado que la carga se transfiriera a través del río por conducción y los pulsos posteriormente detectados por el galvanómetro. Esta fue la primera transmisión inalámbrica mediante electromagnetismo, pero no fue radio.
Morse confió completamente en la conducción para lograr la transmisión inalámbrica y ahora se sabe que necesitamos alternar campos eléctricos y magnéticos para propagar información a distancia sin portadores de carga. Los siguientes pasos en el avance a la radio fueron los experimentos de inducción. Estos culminaron en un experimento de Loomis quien en 1866 envió las primeras señales inalámbricas aéreas utilizando cometas voladas por alambres de cobre [9]. La cometa transmisora tenía una llave Morse en el extremo del suelo y se habría desarrollado un potencial eléctrico entre el suelo y la propia cometa. El cierre de la llave resultó en un flujo de corriente a lo largo del cable y esto creó un campo magnético que se extendió e indujo una corriente en la cometa receptora y esto fue detectado por un galvanómetro. Sin embargo, no se produce gran parte de un campo eléctrico y no se transmite una onda EM. Como tal, el alcance de este sistema es muy limitado. La comunicación inalámbrica práctica requiere una onda EM a una frecuencia lo suficientemente alta como para que pueda generarse de manera eficiente por cables cortos.
1.3.9 Ecuaciones de Maxwell
El siguiente paso esencial en la invención de la radio fue el desarrollo de las ecuaciones de Maxwell en 1861. Antes de que se postularan las ecuaciones de Maxwell, se conocían varias leyes estáticas EM. Estas son la ley Biot—Savart, la ley circuital de Ampere, la ley de Gauss y la ley de Faraday. Tomados en conjunto, no pueden describir la propagación de las señales EM, pero pueden derivarse de las ecuaciones de Maxwell. Las ecuaciones de Maxwell no pueden derivarse de las leyes de campo magnético y eléctrico estático. Las ecuaciones de Maxwell incorporan información adicional que relaciona las derivadas espaciales con las derivadas del tiempo, lo que lleva a una descripción de los campos de propagación. Las ecuaciones de Maxwell son
\[\label{eq:13}\nabla\times\overline{\mathcal{E}}=-\frac{\partial\overline{\mathcal{B}}}{\partial t}-\overline{\mathcal{M}} \]
\[\label{eq:14}\nabla\cdot\overline{\mathcal{D}}=\rho_{V} \]
\[\label{eq:15}\nabla\times\overline{\mathcal{H}}=\frac{\partial\overline{\mathcal{D}}}{\partial t}+ \overline{\mathcal{J}} \]
\[\label{eq:16}\nabla\cdot\overline{\mathcal{B}}=\rho_{mV} \]
Ya se han introducido varias de las cantidades en la ecuación de Maxwell, pero ahora los campos eléctrico y magnético están en forma vectorial. Las otras cantidades en Ecuaciones\(\eqref{eq:13}\) —\(\eqref{eq:16}\) son
- \(\overline{\mathcal{J}}\), la densidad de corriente eléctrica, con unidades de amperios por metro cuadrado (\(\text{A/m}^{2}\));
- \(\rho_{V}\), la densidad de carga eléctrica, con unidades de culombios por metro cúbico (\(\text{C/m}^{3}\));
- \(\rho_{mV}\), la densidad de carga magnética, con unidades de webers por metro cúbico (\(\text{Wb/m}^{3}\)); y
- \(\overline{\mathcal{M}}\), la densidad de corriente magnética, con unidades de voltios por metro cuadrado (\(\text{V/m}^{2}\)).
Las cargas magnéticas no existen, pero su introducción a través de la densidad de carga magnética\(\rho_{mV}\), y la densidad de corriente magnética\(\overline{\mathcal{M}}\), introducen una simetría estéticamente atractiva a las ecuaciones de Maxwell. Las ecuaciones de Maxwell son ecuaciones diferenciales, y como ocurre con la mayoría de las ecuaciones diferenciales, su solución se obtiene con condiciones de límite particulares, que en la ingeniería de radio son impuestas por conductores. Los conductores eléctricos (es decir, paredes eléctricas) soportan cargas eléctricas y, por lo tanto, corriente eléctrica. Por analogía, las paredes magnéticas soportan cargas magnéticas y corrientes magnéticas. Las paredes magnéticas también proporcionan condiciones de límite para ser utilizadas en la solución de las ecuaciones de Maxwell. La noción de paredes magnéticas es importante en la ingeniería de RF y microondas, ya que se aproximan por el límite entre dos dieléctricos de diferente permitividad. Cuanto mayor es la diferencia de permitividad, más cerca se aproxima el límite a una pared magnética.
Las ecuaciones de Maxwell son propiedades fundamentales y no hay ninguna teoría subyacente, por lo que deben ser aceptadas “tal cual”, pero han sido verificadas en innumerables experimentos. Las ecuaciones de Maxwell tienen tres tipos de derivadas. Primero, está la derivada del tiempo,\(\partial /\partial t\). Luego hay dos derivadas espaciales, llamadas curl\(\nabla\times\), capturando la forma en que un campo circula espacialmente (o la cantidad que se acurruca sobre sí mismo)\(\nabla\cdot\), y, llamado operador div, que describen la extensión de un campo. En coordenadas rectangulares, curl,\(\nabla\times\), describe cuánto circunda un campo alrededor de los\(z\) ejes\(x\)\(y\),, y. Es decir, el rizo describe cómo un campo circula sobre sí mismo. Entonces Ecuación\(\eqref{eq:13}\) relaciona la cantidad que un campo eléctrico circula sobre sí mismo con los cambios del\(B\) campo en el tiempo. Entonces una derivada espacial de los campos eléctricos está relacionada con una derivada temporal del campo magnético. También en Ecuación\(\eqref{eq:15}\) la derivada espacial del campo magnético está relacionada con la derivada temporal del campo eléctrico. Estos son los elementos clave que dan como resultado una propagación autosustentable.
Div\(\nabla\cdot\),, describe cómo se extiende un campo desde un punto. Por lo que la presencia de carga eléctrica neta (digamos, en un conductor) dará como resultado que el campo eléctrico se extienda desde un punto (ver Ecuación\(\eqref{eq:14}\)). En contraste, el campo magnético (Ecuación\(\eqref{eq:16}\)) nunca puede divergir de un punto, lo que es resultado de cargas magnéticas no existentes (excepto cuando se utiliza la aproximación de la pared magnética).
La rapidez con que un campo varía con el tiempo,\(\partial\overline{\mathcal{B}}/\partial t\) y\(\partial\overline{\mathcal{D}}/\partial t\), depende de la frecuencia. La propiedad más interesante es la rapidez con la que un campo puede cambiar espacialmente,\(\nabla\times\overline{\mathcal{E}}\) y\(\nabla\times\overline{\mathcal{H}}\) —esto depende de la longitud de onda relativa a la geometría. Entonces, si las dimensiones transversales de una línea de transmisión son menores que una longitud de onda (\(\lambda /2\)o\(\lambda /4\) en diferentes circunstancias), entonces será imposible que los campos se acurruquen sobre sí mismos y así solo habrá una solución (sin variación espacial o mínima de la\(E\) y \(H\)campos) o, en algunos casos, ninguna solución a las ecuaciones de Maxwell.
1.3.10 Transmisión de señales de radio
Ahora la discusión vuelve al desarrollo tecnológico de la radio. Casi al mismo tiempo que los experimentos de inducción de Loomis en 1864, James Maxwell [10] sentó las bases de la teoría moderna EM en 1861 [11]. Maxwell teorizó que los campos eléctricos y magnéticos son diferentes manifestaciones del mismo fenómeno. La conclusión revolucionaria fue que si varían en el tiempo, entonces viajarían por el espacio como una ola. Esta perspicacia fue aceptada casi de inmediato por muchas personas e inició una gran cantidad de esfuerzos. El periodo de 1875 a 1900 fue una época de tremenda innovación en la comunicación inalámbrica.
El 22 de noviembre de 1875, Edison observó chispas EM. Anteriormente se consideraba que las chispas eran un fenómeno de inducción, pero Edison pensó que estaba produciendo un nuevo tipo de fuerza, a la que llamó la fuerza etérica. Creía que esto permitiría la comunicación sin cables. Para poner esto en contexto, el telégrafo se inventó en la década de 1830 y el teléfono se inventó en 1876.
La siguiente etapa conducente a la radio fue orquestada por D. E. Hughes a partir de 1879. Hughes experimentó con una chispa y razonó que en la brecha había una corriente rápidamente alterna y no una corriente constante como otros de su tiempo creían. Nació el oscilador eléctrico. El transmisor de chispa se incrementó con un mecanismo de relojería para interrumpir el circuito transmisor y producir señales de radio pulsadas. Utilizó un teléfono como receptor y caminó por Londres y detectó las señales transmitidas a distancia. Hughes señaló que tuvo buena recepción en\(180\text{ feet}\). Hughes demostró públicamente su “radio” en 1870 ante la Royal Society, pero los eminentes científicos de la sociedad determinaron que el efecto se debía simplemente a la inducción. Esto desanimó a Hughes de continuar. Sin embargo, Hughes tiene un reclamo legítimo de haber inventado la radio, la radio digital móvil en ese momento, y probablemente estaba transmitiendo pulsos en una\(100\text{ kHz}\) portadora. En la radio de Hugeness la portadora de RF fue producida por el oscilador de chispa y la información fue codificada como pulsos. Fue un pequeño salto a un sistema basado en claves Morse.
La invención de la radio práctica puede atribuirse a muchas personas, comenzando por Heinrich Hertz, quien en el periodo de 1885 a 1889 verificó con éxito la predicción esencial de las ecuaciones de Maxwell de que la energía EM podría propagarse a través de la atmósfera. Hertz fue mucho más minucioso que Hughes y sus resultados fueron ampliamente aceptados. En 1891 Tesla desarrolló lo que ahora se llama la bobina Tesla, que es un transformador con una bobina primaria y una secundaria, una dentro de la otra. Cuando una de las bobinas estaba excitada por una señal alterna, se produjo un gran voltaje a través de los terminales de la otra bobina. Tesla persiguió la aplicación de sus bobinas a la radio y se dio cuenta de que las bobinas podían sintonizarse para que la resonancia resultante amplificara enormemente una señal de radio.
El siguiente hito fue el establecimiento del primer sistema de radio práctico por Marconi, con experimentos que comenzaron en 1894. Las oscilaciones se produjeron en una chispa, las cuales fueron amplificadas por una bobina Tesla. La obra culminó con la transmisión de señales telegráficas a través del Atlántico (de Irlanda a Canadá) por Marconi en 1901. En 1904, se podían comprar fácilmente kits de radio de cristal para detectar señales telegráficas inalámbricas.
Los transmisores de chispa solo podían enviar pulsos de ruido y no de voz. Un generador que podía modularse en amplitud era un alternador. Al final
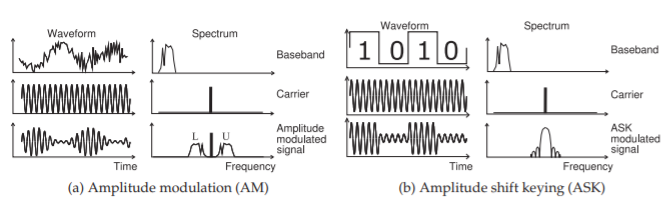
Figura\(\PageIndex{5}\): Forma de onda y espectros de esquemas de modulación simple. La señal moduladora, en la parte superior en (a) y (b), también se llama señal de banda base.
del siglo XIX, los alternadores fácilmente disponibles produjeron una\(60\text{ Hz}\) señal. Reginald Resplendent intentó hacer un alternador de mayor frecuencia y lo mejor que logró operó\(1\text{ kHz}\). Resplandeciente se dio cuenta de que las ecuaciones de Maxwell indicaban que la radiación aumentaba drásticamente con la frecuencia y por lo que necesitaba una fuente de señal de frecuencia mucho más alta. Bajo contrato, General Electric desarrolló un\(2\text{ kW}\)\(100\text{ kHz}\) alternador diseñado por Ernst Alexanderson. Con este alternador, la primera comunicación por radio de voz ocurrió el 23 de diciembre de 1900, en una transmisión de Fsenden desde una isla en el río Potomac, cerca de Washington, DC. Después, el 24 de diciembre de 1906, Fsensiden transmitió voz desde Massachusetts a barcos a cientos de millas de distancia en el Océano Atlántico. Este hito es considerado como el inicio de la era radiofónica.
Posteriormente, Marconi compró alternadores\(50\) y\(200\text{ kW}\) Alexanderson para sus transmisiones transatlánticas. Marconi fue un gran integrador de ideas, siendo logros particulares el diseño de antenas transmisoras y receptoras que pudieran sintonizarse a una frecuencia particular y el desarrollo de un coherer para mejorar la detección de una señal.
1.3.11 Radio Temprana
La radio funciona superponiendo información que varía relativamente lentamente, a lo que se llama la frecuencia de banda base, sobre una sinusoide portadora variando la amplitud y/o fase de la sinusoide. Los primeros sistemas de radio se basaban en modular una portadora oscilante, ya sea mediante la pulsación de la portadora (usando por ejemplo el código Morse) —este esquema de modulación se llama modulación por desplazamiento de amplitud (ASK) —o variando la amplitud de la portadora, es decir, modulación de amplitud ( AM), en el caso de transmisión analógica, generalmente de voz. Las formas de onda y los espectros de estos esquemas de modulación se muestran en la Figura\(\PageIndex{5}\). La información está contenida en la señal de banda base, que también se llama la señal moduladora. El espectro de la señal de banda base se extiende a CC o tal vez hacia abajo hasta donde rueda a baja frecuencia. El portador es una sola onda sinusoidal y no contiene información. La amplitud de la portadora es variada por la señal de banda base para producir la señal modulada. En general, hay muchos ciclos de la portadora en relación con las variaciones de la señal de banda base de modo que el ancho de banda de la señal modulada es relativamente pequeño en comparación con la frecuencia de la portadora.
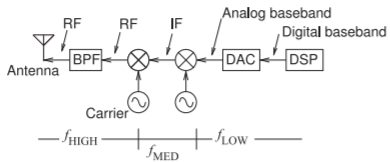
Figura\(\PageIndex{6}\): Un transmisor simple con secciones de baja\(f_{\text{LOW}}\)\(f_{\text{MED}}\), media y alta frecuencia.\(f_{\text{HIGH}}\) Los mezcladores pueden idealizarse como multiplicadores, mostrados como círculos con cruces, que potencian la frecuencia de la banda base de entrada o señal IF por la frecuencia de la portadora.
Las radios AM y ASK son sistemas de comunicación de banda estrecha (utilizan una pequeña porción del espectro EM), por lo que para evitar interferencias con otras radios es necesario buscar una parte abierta del espectro para colocar la señal portadora. En la década del siglo XX había poca organización y un oyente necesitaba buscar para encontrar la transmisión deseada. La tecnología del día requería esto de todos modos, ya que el portador se desplazaría alrededor\(10\%\) o menos ya que entonces no era posible construir un oscilador estable. No fue hasta el hundimiento del Titanic en 1912 que se impuso la regulación a la industria inalámbrica. Las investigaciones sobre el hundimiento del Titanic concluyeron que la mayoría de las vidas perdidas se habrían salvado si una nave cercana hubiera estado monitoreando sus canales de radio y si se fijara la frecuencia del canal de emergencia. No obstante, un segundo barco, pero no lo suficientemente cerca, sí respondió a la señal “SOS” de Titanic. Resultado de las investigaciones fue el Reglamento de Servicio de la Convención Internacional de Radiotelégrafos de Londres de 1912.
Estas primeras regulaciones eran bastante liberales y a las estaciones de radio se les permitía usar longitudes de onda de radio de su elección, pero restringidas a cuatro bandas anchas: una sola banda en\(1500\text{ kHz}\) para aficionados;\(187.5\) a\(500\text{ kHz}\), apropiadas principalmente para uso gubernamental; abajo\(187.5\text{ kHz}\) para uso comercial, y\(500\text{ kHz}\) a\(1500\text{ kHz}\), también una banda comercial. Los años posteriores vieron una asignación más estricta de bandas espectrales estrechas y la asignación de canales. Se establecieron los estándares y el entorno regulatorio para la radio, se asignarían bandas de frecuencia para fines particulares. Muy rápidamente fuertes intereses gubernamentales y comerciales lucharon por el uso exclusivo de bandas particulares y así el espectro EM desarrolló un valor considerable. Las entidades “poseían” porciones del espectro ya sea a través de una licencia o mediante asignación gubernamental.
Si bien la mayor parte del espectro está asignado, existen varias bandas abiertas donde no se requieren licencias. Las bandas de instrumentación, científica y médica (ISM) en\(2.4\) y\(5.8\text{ GHz}\) son ejemplos. Dado que estas bandas están reguladas libremente, las radios deben hacer frente a niveles potencialmente altos de interferencia.
Notas al pie
[1] El código Morse utiliza secuencias de puntos, guiones y espacios. La duración de un guión (o “dah”) es tres veces mayor que la de un punto (o “dit”). Entre letras hay un pequeño hueco. Por ejemplo, el código Morse para PI es “. - -.”. Entre palabras hay una pausa un poco más larga y entre oraciones una pausa aún más larga. Tabla\(\PageIndex{3}\) enumera el código Morse internacional adoptado en 1848. El código Morse original desarrollado en la década de 1830 se conoce ahora como “código Morse estadounidense” o “código ferroviario”. El “código Morse internacional moderno” extiende el código Morse internacional con secuencias para letras no inglesas y símbolos especiales.