2.2: Métricas de señal de radio

Las señales de radio están diseñadas para compensar el uso eficiente del espectro EM con la complejidad y el rendimiento del hardware de RF requerido. En última instancia, el objetivo es usar eficientemente el espectro a través del empaque máximo de información, por ejemplo, bits digitales, en un ancho de banda dado, mientras que, especialmente para radios móviles, se usa la menor potencia principal posible. La elección del tipo de modulación a utilizar está en el núcleo de la compensación de diseño del sistema de comunicación.

Existen dos familias de métodos de modulación: modulación analógica y digital. En la modulación analógica la señal RF tiene un rango continuo de valores; en la modulación digital, la salida tiene una serie de estados discretos en momentos particulares llamados ticks de reloj, digamos cada microsegundo. Solo hay algunos esquemas de modulación, todos los cuales son digitales, que logran las compensaciones óptimas de eficiencia espectral y facilidad de uso con una complejidad de hardware aceptable. Si la complejidad del hardware no es una preocupación, qué esquema de modulación se usa depende del ruido y la interferencia, así como de la potencia requerida para transmitir una señal, y la potencia requerida para procesar una señal recibida.

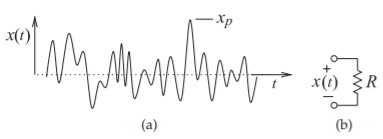
Figura\(\PageIndex{1}\): Definición de factor de cresta: (a) forma de onda arbitraria; y (b) voltaje a través de una resistencia.

Esta sección introduce varias métricas que caracterizan la variabilidad de la amplitud de una señal modulada, y esta variabilidad tiene un impacto directo en cómo se diseñan los rendimientos del hardware analógico y la eficiencia en que se puede usar el hardware.

2.2.1 Factor de cresta y relación de potencia pico a promedio

Introducción

En ingeniería de radio, el factor de cresta (CF) es una métrica que describe cómo varía el voltaje de una señal portadora modulada con el tiempo, y la relación de potencia pico a promedio (PAPR) describe cómo la potencia instantánea de una señal portadora varía con el tiempo. Tenga en cuenta que hay una métrica, la relación pico-promedio (PAR), que se define de manera diferente en las comunidades de poder, teoría de las comunicaciones y microondas. En algunas comunidades, la FQ también se llama la relación pico-promedio (PAR). Esto puede llevar a problemas. Considere, por ejemplo, la comunidad que trabaja en la medición inteligente de energía que combina la medición de potencia, la teoría de las comunicaciones y el diseño de microondas. La solución a esta inevitable confusión es omitir el uso de PAR y usar métricas inequívocas.

Nota

En los estándares PAR se define como la relación entre el valor pico instantáneo de un parámetro de señal y su valor promediado en el tiempo. PAR se usa con muchos parámetros de señal, por ejemplo, voltaje, corriente, potencia y frecuencia [1].

Factor de cresta

CF es la relación de la señal máxima, tal como una tensión, a su valor de raíz-meansquare (rms). Haciendo referencia a la forma de onda arbitraria mostrada en la Figura\(\PageIndex{1}\) (a),\(x_{p}\) es el valor máximo absoluto de la forma de onda\(x(t)\), si\(x_{\text{rms}}\) es su valor rms, entonces el factor de cresta es [2]

\[\label{eq:1} \text{CF}=x_{p}/x_{\text{rems}} \]

De manera más formal,

\[\label{eq:2}\text{CF}=\frac{\| x \|_{\infty}}{\| x\|_{2}} \]

donde\(\|x\|_{∞}\) está la norma del infinito, y aquí está el valor máximo de\(x(t)\),\(\|x\|_{∞} = \text{max}[x(t)] = x_{p}\), y\(\|x\|_{2}\) es solo el valor rms de\(x(t)\):

\[\label{eq:3}x_{\text{rms}}=\|x\|_{2}=\lim_{T\to\infty}\sqrt{\frac{1}{T}\int_{0}^{T}x(t)\cdot dt} \]

Tenga en cuenta que CF es una relación de voltaje (o corriente) en lugar de una relación de potencia. Los CFs de varias formas de onda se dan en la Tabla\(\PageIndex{1}\).

Relación de potencia pico a promedio (PAPR)

La relación de potencia pico a promedio (PAPR) es análoga a la CF pero para la potencia. Si\(x(t)\) es el voltaje a través de una resistencia, como se muestra en la Figura\(\PageIndex{1}\) (b), entonces el

Forma de onda	\(x(t)\)	Valor máx.	rms\((x_{\text{rms}})\)	CF	PAPR
DC	\ (x (t)\) ">	\(x_{\text{dc}}\)	\ ((x_ {\ text {rms}})\) ">\(x_{\text{dc}}\)	\(1\)	\(0\text{ dB}\)
Onda sinewave	\ (x (t)\) ">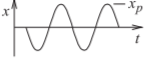	\(x_{p}\)	\ ((x_ {\ text {rms}})\) ">\(\frac{x_{p}}{\sqrt{2}}\)	\(1.414\)	\(3.01\text{ dB}\)
Onda sinusoidal rectificada de onda completa	\ (x (t)\) ">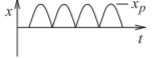	\(x_{p}\)	\ ((x_ {\ text {rms}})\) ">\(\frac{x_{p}}{\sqrt{2}}=0.717x_{p}\)	\(1.414\)	\(3.01\text{ dB}\)
Onda senoidal rectificada de media onda	\ (x (t)\) ">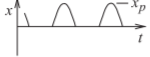	\(x_{p}\)	\ ((x_ {\ text {rms}})\) ">\(\frac{x_{p}}{2}\)	\(2\)	\(6.02\text{ dB}\)
Onda triangular	\ (x (t)\) ">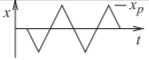	\(x_{p}\)	\ ((x_ {\ text {rms}})\) ">\(\frac{x_{p}}{\sqrt{3}}=0.577x_{p}\)	\(1.732\)	\(4.77\text{ dB}\)
Onda cuadrada	\ (x (t)\) ">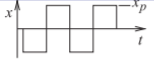	\(x_{p}\)	\ ((x_ {\ text {rms}})\) ">\(x_{p}\)	\(1\)	\(0\text{ dB}\)

Mesa\(\PageIndex{1}\)

la potencia pico instantánea en la resistencia es

\[\label{eq:4}P_{p}=|x_{p}|^{2}/R \]

donde de nuevo\(x_{p}\) es el valor absoluto pico de la forma de onda. \(P_{p}\)es la potencia del pico de una forma de onda tratándola como si fuera una señal de CC. Esto es apropiado para una señal que varía lentamente, como una señal de frecuencia de potencia, ya que es esta potencia instantánea la que determina la interrupción térmica de un sistema de energía. No es la potencia adecuada para usar con señales de radio y una métrica de señal de microondas más adecuada se describe en la Sección 2.2.2. La potencia promedio disipada en la resistencia es

\[\label{eq:5}P_{\text{avg}}=|x_{\text{rms}}|^{2}/R \]

Entonces

\[\label{eq:6}\text{PAPR}=\frac{P_{p}}{P_{\text{avg}}}=\text{CF}^{2}=(x_{p}/x_{\text{rms}})^{2} \]

En decibelios,

\[\begin{align}\text{PAPR}|_{\text{dB}}&=10\log (\text{PAPR})\nonumber \\ \label{eq:7}&=20\log (\text{CF})=20\log (x_{p}/x_{\text{rms}})\end{align} \]

La definición de PAPR anterior se puede utilizar con cualquier forma de onda y puede ser utilizada en todas las ramas de la ingeniería eléctrica. Las PAPR de varias formas de onda se dan en la Tabla\(\PageIndex{1}\).

Ejemplo\(\PageIndex{1}\): Crest Factor and PAPR of an Offset Sinusoid

¿Cuál es el factor de cresta (CF) y la relación de potencia pico a promedio (PAPR) de la señal\(x(t) = 0.1+0.5 \sin(\omega t)\)?

Solución

La señal es un desplazamiento sinusoidal por un término de CC. El valor pico de\(x(t)\) es\(x_{p} = 0.6\), y el valor rms de la señal será la raíz cuadrada de los valores rms al cuadrado de los componentes individuales de CC y sinusoidales. Esto se aplica a cualquier señal compuesta siempre que los componentes no estén correlacionados. Entonces\(x_{\text{rms}} = \sqrt{ 0.12 + (0.5/\sqrt{2})^{2}} = 0.3674\). La solución general para una señal\(x(t) = a + b \sin(\omega t)\) es, usando Ecuación\(\eqref{eq:3}\),

\[\begin{align}x_{\text{rms}}&=\sqrt{\lim_{T\to\infty}\frac{1}{T}\int_{0}^{T}\left[x(t)\right]^{2} dt}=\sqrt{\lim_{T\to\infty}\frac{1}{T}\int_{0}^{T}\left[a+b\sin (\omega t)\right]^{2} dt}\nonumber \\ &=\sqrt{\lim_{T\to\infty}\frac{1}{T}\int_{0}^{T}\left[a^{2}+ab\sin (\omega t)+b^{2}\sin^{2}(\omega t)\right]dt}\nonumber \\ &=\sqrt{\lim_{T\to\infty}\frac{1}{T}\left\{\int_{0}^{T}a^{2} dt +\int_{0}^{T}ab\sin (\omega t)dt+\int_{0}^{T}b^{2}\frac{1}{2}\left[1+\cos (2\omega t)\right] dt\right\}}\nonumber \\ \label{eq:8} &=\sqrt{\lim_{T\to\infty}\frac{1}{T}\left\{a^{2}T dt+0+\frac{1}{2}b^{2}T\right\}}\end{align} \]

ya que la integral de\(\sin\) y\(\cos\) durante un periodo es cero. Así

\[\label{eq:9}x_{\text{rms}}=\sqrt{a^{2}+b^{2}/2}=\sqrt{0.1^{2}+\frac{1}{2}0.5^{2}}=0.3674 \]

el factor de cresta es

\[\label{eq:10}\text{CF}=\frac{x_{p}}{x_{\text{rms}}}=\frac{0.6}{0.3674}=1.6311 \]

y PAPR es

\[\label{eq:11}\text{PAPR}=20\log (1.6311)=4.260\text{ dB} \]

Hay una manera más rápida de calcular PAPR tratando directamente con los poderes. La potencia pico de la forma de onda es\(P_{p} = x_{p}^{2}/R = 0.6^{2}/R = 0.36/R\), donde\(x\) se trata como una tensión a través de una resistencia\(R\). Las dos partes de\(x(t)\), es decir, la componente DC y la onda senoidal, no están correlacionadas, por lo que la potencia promedio de la señal combinada es la suma de las potencias de los componentes no correlacionados, por lo que

\[\label{eq:12}P_{\text{avg}}=\frac{1}{R}\left[0.1^{2}+\frac{1}{2}0.5^{2}\right]\frac{1}{R}=\frac{0.1350}{R} \]

Así, en decibelios,

\[\label{eq:13}\text{PAPR}|_{\text{dB}}=10\log\left(\frac{P_{p}}{P_{\text{avg}}}\right)=\frac{x_{p}^{2}}{x_{\text{rms}}^{2}}=10\log\left(\frac{0.36}{0.135}\right)=10\log (2.667)=4.260\text{ dB} \]

2.2.2 Relación de potencia de envolvente pico a media

Otra métrica para caracterizar señales es la relación de potencia de envolvente pico a media (PMEPR) y esto es particularmente útil para señales moduladas. La cantidad de información enviada por una señal de comunicación es proporcional a su potencia promedio, sin embargo, el hardware de RF debe diseñarse con suficiente margen para poder manejar picos en la señal sin producir distorsión apreciable. La forma de onda de una señal modulada de banda estrecha aparece como una portadora que cambia lentamente en amplitud y fase. Una onda senoidal de esta señal modulada se denomina pseudo-portadora y la potencia de un ciclo de la pseudo-portadora cuando la amplitud de la señal modulada está en su máximo (es decir, en el pico de la envolvente) se denomina potencia de envolvente pico (PEP) [1] (\(\text{PEP} = P_{\text{PEP}}\)). La relación de PEP a la potencia promedio de la señal (la potencia promediada en todos los tiempos) se llama PMEPR.

Entonces, si la potencia promedio de la señal modulada es\(P_{\text{avg}}\)

\[\label{eq:14}\text{PMEPR}=\frac{\text{PEP}}{P_{\text{avg}}}=\frac{P_{\text{PEP}}}{P_{\text{avg}}} \]

PMEPR es un buen indicador de cuán sensible es un formato de modulación a la distorsión introducida por la no linealidad del hardware de RF [3].

Es complejo determinar el PMEPR para una señal modulada general. A continuación se presentan las matemáticas para una señal AM con una señal moduladora sinusoidal. Determinar el PMEPR de otra manera requiere integración numérica siguiendo el procedimiento que se describe a continuación.

PMEPR de una señal AM

Se puede obtener una buena estimación del PMEPR de una señal AM considerando una señal de modulación sinusoidal (en lugar de una señal de banda base real). Dejar\(y(t) = \cos (2πf_{m}t)\) ser una señal moduladora cosinusoidal con frecuencia\(f_{m}\). Entonces, para AM, la señal portadora modulada es

\[\label{eq:15}x(t)=A_{c}\left[1+m\cos (2\pi f_{m}t)\right]\cos (2\pi f_{c}t) \]

donde\(m\) está el índice de modulación (por ejemplo,\(100\%\) AM tiene\(m = 1\)). Así, si se considera la potencia de solo un cuasi-periodo de\(x(t)\), es decir, un ciclo de la pseudo portadora, entonces\(x(t)\) tiene una potencia que varía con el tiempo.

Considere un voltaje\(v(t)\) a través de una resistencia de conductancia\(G\). La potencia de la señal se determina integrando sobre todo el tiempo, que es trabajo, y dividiendo por el periodo de tiempo. Esto produce la potencia promedio:

\[\label{eq:16}P_{\text{avg}}=\lim_{\tau\to\infty}\int_{-\tau}^{\tau}\frac{1}{2\tau}Gv^{2}(t)dt \]

Ahora bien, si\(v(t)\) es sinusoidal\(v(t) = A \cos\omega t\), entonces

\[\begin{align}P_{\text{avg}}&=\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}A_{c}^{2}G\cos^{2}(\omega t)dt\nonumber \\ &=\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}A_{c}^{2}G\frac{1}{2}\left[1+\cos (2\omega t)\right] dt \nonumber \\ \label{eq:17}&=\frac{1}{2}A_{c}^{2}G\left\{\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}1 dt+\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\cos (2\omega t)dt\right\}=\frac{1}{2}A_{c}^{2}G\end{align} \]

En la ecuación anterior, se ha empleado una equivalencia útil al observar que la integral infinita de una cosinusoide puede simplificarse a solo integrarse en un periodo,\(T = 2π/\omega\):

\[\label{eq:18}\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\cos^{n}(\omega t)dt=\frac{1}{T}\int_{-T/2}^{T/2}\cos^{n}(\omega t) dt \]

donde\(n\) es un entero positivo. En los cálculos de potencia existen otras técnicas útiles de simplificación basadas en identidades trigonométricas. Algunos de los que se utilizarán aquí son los siguientes:

\[\begin{align} \cos A\cos B&=\frac{1}{2}\left[\cos (A-B)+\cos (A+B)\right]\nonumber \\ \label{eq:19} \cos^{2}A&=\frac{1}{2}\left[1+\cos (2A)\right] \\ \label{eq:20}\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\cos\omega t dt&=\frac{1}{T}\int_{-T/2}^{T/2}\cos (\omega t)dt=0 \\ \label{eq:21}\frac{1}{T}\int_{-T/2}^{T/2}\cos^{2}(\omega t)dt&=\frac{1}{T}\int_{-T/2}^{T/2}\frac{1}{2}\left[\cos (2\omega t)+\cos (0)\right] \\ &=\frac{1}{2T}\left[\int_{-T/2}^{T/2}\cos (2\omega t)dt+\int_{-T/2}^{T/2}1 dt\right] \\ \label{eq:22} &=\frac{1}{2T}(0+T)=\frac{1}{2}\end{align} \]

Se dan más identidades trigonométricas en el Apéndice 1.A.2 de [4]. Además, cuando los cosinusoides\(\cos\omega_{A}t\) y\(\cos\omega_{B}t\), teniendo diferentes frecuencias (\(\omega_{A}\neq\omega_{B}\)), se multiplican juntos, para grandes\(\tau\),

\[\int_{-\tau}^{\tau}\cos\omega_{A}t\cos\omega_{B}t dt=\int_{-\tau}^{\tau}\frac{1}{2}\left[\cos (\omega_{A}+\omega_{B})t+\cos (\omega_{A}-\omega_{B})t\right] dt=0\nonumber \]

y si\(\omega_{A}\neq\omega_{B}\neq 0\)

\[\label{eq:23}\int_{-\infty}^{\infty}\cos\omega_{A}t\cos^{n}\omega_{B}tdt=0 \]

Ahora la discusión vuelve a caracterizar una señal AM al considerar la potencia promedio a largo plazo y la potencia máxima a corto plazo de la señal. La pseudo-portadora en su amplitud máxima es, de la Ecuación\(\eqref{eq:15}\),

\[\label{eq:24}x_{p}(t)=A_{c}[1+m]\cos (2\pi f_{c}t) \]

Entonces la potencia (\(P_{\text{PEP}}\)) de la pseudo portadora pico se obtiene integrando a lo largo de un periodo de la pseudo portadora:

\[\begin{align} P_{\text{PEP}}&=\frac{1}{T}\int_{-T/2}^{T/2}Gx^{2}(t)dt=\frac{1}{T}\int_{-T/2}^{T/2}A_{c}^{2}G(1+m)^{2}\cos^{2}(\omega_{c}t)dt\nonumber \\ \label{eq:25} &=A_{c}^{2}G(1+m)^{2}\frac{1}{T}\int_{-T/2}^{T/2}\cos^{2}(\omega_{c}t)dt=\frac{1}{2}A_{c}^{2}G(1+m)^{2}\end{align} \]

La potencia promedio (\(P_{\text{avg}}\)) de la señal modulada se obtiene integrando sobre todo el tiempo, por lo que

\[\begin{align} P_{\text{avg}}&=\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}Gx^{2}(t)dt\nonumber \\ &=A_{c}^{2}G\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\{[1+m\cos (\omega_{m}t)]\cos (\omega_{c}t\}^{2}dt\nonumber \\&=A_{c}^{2}G\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\{[1+2m\cos (\omega_{m}t)+m^{2}\cos^{2}(\omega_{m}t)]\cos^{2}(\omega_{c}t)\}dt\nonumber \\&=A_{c}^{2}G\left[\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\cos^{2}(\omega_{c}t)dt+\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}2m\cos (\omega_{m}t)\cos^{2}(\omega_{c}t)dt \right.\nonumber \\ &\quad \left. +\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}m^{2}\cos^{2}(\omega_{m}t)\cos^{2}(\omega_{c}t)dt\right]\nonumber \\ &=A_{c}^{2}G\left\{\frac{1}{2}+0+m^{2}\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\frac{1}{4}\left[1+\cos (2\omega_{m}t)\right]\left[1+\cos (2\omega_{c}t)\right] dt\right\}\nonumber \\ &=A_{c}^{2}G\left\{\frac{1}{2}+\frac{m^{2}}{4}\left[\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}1 dt+\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\cos (2\omega_{m}t) dt\right.\right.\nonumber \\ &\quad\left.\left. +\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\cos (2\omega_{c}t)dt+\lim_{\tau\to\infty}\frac{1}{2\tau}\int_{-\tau}^{\tau}\cos (2\omega_{m}t)\cos (2\omega_{c}t)dt\right]\right\} \nonumber \\ \label{eq:26} &=A_{c}^{2}G\left[\frac{1}{2}+m^{2}\left(\frac{1}{4}+0+0+0\right)\right] =\frac{1}{2}A_{c}^{2}G(1+m^{2}/2)\end{align} \]

Así el voltaje rms,\(x_{\text{rms}}\), se puede determinar como\(P_{\text{avg}} = x_{\text{rms}}^{2}G\). Entonces el PMEPR de una señal AM (i.e.,\(\text{PMEPR}_{\text{AM}}\)) es

\[\text{PMEPR}_{\text{AM}}=\frac{P_{\text{PEP}}}{P_{\text{avg}}}=\frac{\frac{1}{2}A_{c}^{2}G(1+m)^{2}}{\frac{1}{2}A_{c}^{2}G(1+m^{2}/2)}=\frac{(1+m)^{2}}{1+m^{2}/2}\nonumber \]

Para\(100\%\) AM descrito por\(m = 1\), el PMEPR es

\[\label{eq:27}\text{PMEPR}_{100\%\text{AM}}=\frac{(1+1)^{2}}{1+1^{2}/2}=\frac{4}{1.5}=2.667=4.26\text{ dB} \]

Al expresar el PMEPR en decibelios, la fórmula\(\text{PMEPR}_{\text{dB}} = 10 \log (\text{PMEPR})\) se usa ya que PMEPR es una relación de potencia. Como ejemplo, para\(50\%\) AM, descrito por\(m = 0.5\), el PMEPR es

\[\label{eq:28}\text{PMEPR}_{50\%\text{AM}}=\frac{(1+0.5)^{2}}{1+0.5^{2}/2}=\frac{2.25}{1.125}=2=3\text{ dB} \]

2.2.3 Señal de dos tonos

Al evaluar, ya sea a través de mediciones de laboratorio o simulaciones, es común y muchas veces necesario utilizar representaciones muy simples de una señal de banda base o incluso de una señal modulada. Esto simplifica enormemente las cosas y existe una expectativa justificada de que el rendimiento con la señal de prueba sea una buena indicación de rendimiento con una señal de banda base o modulada real. Con la simulación a nivel de circuito suele ser imposible considerar señales de banda base reales ya que la simulación puede no ser posible o la simulación puede tomar tiempos inaceptables. En cambio, es común usar señales de un solo tono, es decir, de onda sinusoidal simple o de dos tonos. Una señal de dos tonos es una señal que es la suma de dos cosinusoides:

\[\label{eq:29}y(t)=X_{A}\cos (\omega_{A}t)+X_{B}\cos (\omega_{B}t) \]

Generalmente las frecuencias de los dos tonos son cercanas\((|\omega_{A} −\omega_{B}| ≪ \omega_{A})\), con el concepto de que ambos tonos encajan dentro de la banda de paso de los filtros de paso de banda de un transmisor o receptor. Una señal de dos tonos no es una forma de modulación, sino que se usa comúnmente para caracterizar el rendimiento no lineal de los sistemas de RF y tiene una envolvente que es similar a la de muchas señales moduladas. La señal compuesta,\(y(t)\), parece una pseudo-portadora con una amplitud que varía lentamente, no muy diferente a una señal AM. Los tonos no están correlacionados de manera que la potencia promedio de la señal compuesta,\(y(t)\), es la suma de las potencias de cada uno de los tonos individuales. La potencia pico de la señal compuesta es la de la pseudo-portadora pico, por lo que\(y(t)\) tiene una amplitud pico de\(X_{A} + X_{B}\). La pseudo portadora pico es la sinusoide RF única donde la sinusoide de cada sinusoide se alinea tanto como sea posible. Conceptos similares se aplican a las señales\(n\) de tres tonos y tonos.

Ejemplo\(\PageIndex{2}\): PMEPR of a Two-Tone Signal

¿Cuál es el PMEPR de una señal de dos tonos con los tonos que tienen igual amplitud?

Solución

Que las amplitudes de los dos tonos sean\(X_{A}\) y\(X_{B}\). Ahora\(X_{A} = X_{B} = X\), y así la pseudo-portadora pico tiene amplitud\(2X\), y la potencia de la portadora de RF pico es proporcional a\(\frac{1}{2}(2X)^{2} = 2X^{2}\). El poder promedio es proporcional a\(\frac{1}{2}(X_{A}^{2}+X_{B}^{2}) =\frac{1}{2}(X_{2} + X+{2}) = X_{2}\), ya que cada tono es independiente del otro y así se pueden sumar los poderes.

\[\label{eq:30}\text{PMEPR}=\frac{P_{\text{PEP}}}{P_{\text{avg}}}=\frac{2X^{2}}{X^{2}}=2=3\text{ dB} \]

Ejemplo\(\PageIndex{3}\): PMEPR of Uncorrelated Signals

Considere la combinación de dos señales analógicas no correlacionadas, por ejemplo, una señal de dos tonos. Se denota una señal\(x(t)\) y la otra\(y(t)\), donde\(x(t)=0.1 \sin (10^{9}t)\) y\(y(t) = 0.05 \sin (1.01 · 10^{9}t)\). ¿Cuál es el PMEPR de esta señal combinada?

Solución

Estas dos señales no están correlacionadas y esto es clave para determinar la potencia promedio,\(P_{\text{avg}}\), ya que la suma de las potencias de cada señal individual (\(k\)es una constante de proporcionalidad):

\[P_{\text{avg}}=\int_{-\infty}^{\infty}x^{2}(t)\cdot dt+\int_{-\infty}^{\infty}y^{2}(t)\cdot dt=\frac{k}{2}(0.1)^{2}+\frac{k}{2}(0.5)^{2}=\frac{k}{2}[0.01+0.0025]=0.00625k\nonumber \]

Las dos portadoras son cercanas en frecuencia de modo que la señal suma\(z(t) = x(t) + y(t)\) parece una señal que varía lentamente con una frecuencia de radianes cerca de\(10^{9}\) rads por segundo. La amplitud máxima de un pseudo-ciclo de\(z(t) is 0.1+0.05 = 0.15\). Así, el poder del ciclo más grande es

\[P_{\text{PEP}}=\frac{1}{2}k(0.15)^{2}=0.01125k\nonumber \]

y así

\[\label{eq:31}\text{PMEPR}=\frac{P_{\text{PEP}}}{P_{\text{avg}}}=\frac{0.01125}{0.00625}=1.8=2.55\text{ dB} \]

Resumen

El PMEPR es un atributo importante de un formato de modulación e impacta en los tipos de diseños de circuitos que se pueden usar. Es mucho más difícil desarrollar hardware de bajo consumo que introduzca solo bajos niveles de distorsión cuando el PMEPR es alto.

Es tentador considerar si se pueden eludir las largas integraciones. Se pueden agregar potencias si los componentes de la señal (los tonos que componen la señal) no están correlacionados. Si están correlacionados, entonces se requieren las integraciones completas. Considere dos sinusoides no correlacionados de potencias (promedio)\(P_{1}\) y\(P_{2}\), respectivamente, entonces la potencia promedio de la señal compuesta es\(P_{\text{avg}} = P_{1} + P_{2}\). Sin embargo, al determinar la potencia sinusoidal pico, se considera el ciclo de RF donde se alinean las dos sinusoides pseudo-portadoras más grandes, y aquí los voltajes se suman para producir un solo ciclo de una onda senoidal con una amplitud mayor. Por lo tanto, la potencia máxima se aplica a un solo pseudo-ciclo de RF. Generalmente se sumaría la amplitud de voltaje de las dos ondas senoidales y luego se calcularía la potencia. Si las portadoras no correlacionadas se modulan y las señales moduladoras (las señales de banda base) no están correlacionadas, entonces la potencia promedio se puede determinar de la misma manera, pero el cálculo de la potencia máxima es mucho más complicado. Las integraciones son los únicos cálculos en los que siempre se puede confiar y se pueden usar con todas las señales moduladas.

Nota

\(x(t)\)Señala y no\(y(t)\) están correlacionadas si la integral sobre todos los desplazamientos de tiempo y tiempo de su producto es cero:\(C =\int_{-\infty}^{+\infty} x(t)y(t+\tau ) dt = 0\) para todos\(\tau\).

El uso preferido de PAR, PAPR o PMEPR en ingeniería de RF y microondas se encuentra actualmente en una fase de transición. El uso más común de PAR y PAPR en ingeniería eléctrica se refiere al pico de una señal como el valor pico instantáneo, y en el caso de PAPR, la potencia instantánea de la señal se calcula como si el pico fuera un valor de CC. En el pasado, muchas publicaciones de RF y microondas han tomado el pico como la potencia pico de una sinusoide que tiene una amplitud igual a la tensión pico de la señal y lo usaron para calcular PAR. Este uso es inconsistente con el uso predominante en ingeniería eléctrica y es un problema particular cuando se utiliza tecnología inalámbrica en otras disciplinas. PMEPR es el uso preferido para lo que los ingenieros de RF y microondas pretenden referirse al usar el término PAR. Un lector de literatura de RF que encuentre PAR necesita determinar cómo se está utilizando el término. No hay confusión si se usa PMEPR.

Ejemplo\(\PageIndex{4}\): PAPR and PMEPR of an AM Signal

¿Qué es el PAPR y el PMEPR de una señal\(100\%\) AM?

Solución

La señal es\(x(t) = A_{c} [1 + \cos 2πf_{m}t] \cos 2πf_{c}t\) y el PMEPR de esta señal, de la Ecuación\(\eqref{eq:27}\), es\(4.26\text{ dB}\). Ahora PAPR utiliza el valor máximo absoluto de la señal en lugar de la potencia máxima a corto plazo de la envolvente. El valor pico de\(x(t)\) es\(2A_{c}\) así que la potencia pico (si la señal es un voltaje a través de una conductancia\(G\)) es

\[\label{eq:32} P_{\text{peak, PAPR}}=(2A_{c})^{2}G \]

\(P_{\text{avg}}\)es lo mismo para PAPR y PMEPR para la señal AM, ver Ecuación\(\eqref{eq:26}\), para que

\[\label{eq:33}\text{PAPR}=\frac{P_{\text{peak, PAPR}}}{P_{\text{avg}}}=\frac{(2A_{c})^{2}G}{\frac{1}{2}A_{c}^{2}(1+\frac{1}{2})}=\frac{4}{3/4}=\frac{16}{3}=5.333=7.27\text{ dB} \]

Entonces PAPR es\(3\text{ dB}\) mayor que PMEPR para una señal AM\(100\%\) modulada, ver Ecuación\(\eqref{eq:27}\). Esto no siempre es el caso de otros esquemas de modulación.