3.9: Receptor SDR

Un receptor SDR implementa la demodulación mostrada en la Figura 3.10.24 (a) en dos etapas con demodulación analógica en cuadratura RF en la primera etapa similar a la mostrada en la Figura 3.10.24 (b). Hay mucho detalle en esta sección pero esto es necesario para entender la implementación de un receptor SDR a nivel de diseño.

El diagrama de bloques de una implementación particular de un receptor SDR se muestra en la Figura\(\PageIndex{1}\) que tiene una primera etapa en el dominio analógico implementada en un chip de módem RF, y una segunda etapa digital que implementa DSP en el chip de banda base. Si bien estos son chips separados al momento de escribir este artículo probablemente se combinarán en un solo chip algún día.

La porción analógica del receptor SDR se muestra en la Figura\(\PageIndex{1}\). Esta primera etapa separa los canales I y Q y emite señales de frecuencia de banda base que se muestrean y se ingresan a una segunda etapa de demodulación en cuadratura para producir las señales de banda base finales. Esta segunda etapa se implementa digitalmente. Las señales en la salida de la primera etapa analógica también se denominan frecuencias intermedias. La demodulación digital, a la derecha en la Figura\(\PageIndex{1}\), se realiza en una unidad DSP comúnmente conocida como un chip de módem de banda base. Un atributo clave es que la frecuencia LO de la primera etapa de demodulación, se\(f_{\text{LO}}\) puede establecer en relativamente pocos valores discretos mientras que el LO en la segunda etapa,\(f_{\text{LO, IF}}\) se establece finamente para la recuperación completa de la portadora. En conjunto\(f_{\text{LO}} + f_{\text{LO, IF}} = f_{c}\), la frecuencia de la portadora de la señal recibida\(s(t)\). La unidad DSP puede implementar decodificación tal como decodificación CDMA u OFDM.

El resto de esta sección rastrea el flujo de señal a través del receptor SDR. La señal presentada al demodulador es\(G_{L}s(t)\) donde\(s(t)\) está la señal DSB-SC transmitida en la Ecuación (3.9.1). \(G_{L}\), que será muy pequeña, es la ganancia de enlace que representa la pérdida en la transmisión y la ganancia del receptor y, en ausencia

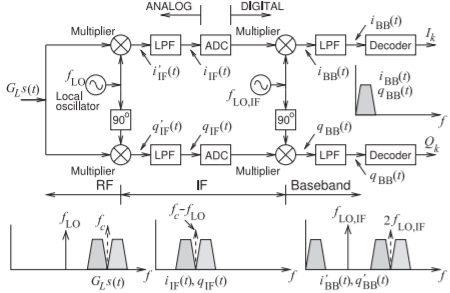
Figura\(\PageIndex{1}\): Receptor SDR con señal de entrada RF\(G_{L}s(t)\) con la primera frecuencia LO,\(f_{\text{LO}}\), menor que la señal portadora\(f_{c}\). Tenga en cuenta que\(2f_{\text{LO, IF}} = f_{c} − f_{\text{LO}}\).

de interferencia,\(s(t)\) es la señal de radio transmitida.

3.12.1 Demodulación del componente I

Si la señal transmitida es la señal DSB-SC\(s(t)\) con portadora\(f_{c}\) en la Ecuación (3.9.1) (reemplazando\(\omega_{\text{LO}}\) por\(f_{c}\)) entonces la señal presentada al demodulador en el receptor es\(G_{L}s(t)\) donde\(G_{L}\), que será muy pequeña, es la ganancia del enlace que representa la pérdida en transmisión y ganancia del receptor. El espectro de la señal DSB-SC recibida,\(G_{L}s(t)\), se muestra en la parte inferior izquierda de la Figura\(\PageIndex{1}\) con la frecuencia portadora\(f_{c}\) identificada por la flecha de trazos. También se muestra la frecuencia LO del primer demodulador at\(f_{\text{LO}}\). El componente en fase de la señal demodulada después del primer demodulador en cuadratura es, ver Figura\(\PageIndex{1}\),

\[\begin{align}i_{\text{IF}}'(t)&=G_{L}s(t)\sin(\omega_{\text{LO}}t)\nonumber \\ &=\frac{1}{2}[A_{i}(f_{i})\cos(\omega_{c}-\omega_{i})t+A_{q}(f_{q})\sin(\omega_{c}-\omega_{q})t\nonumber \\ &\quad - A_{i}(f_{i})\cos(\omega_{c}+\omega_{i})t+A_{q}(f_{q})\sin(\omega_{c}+\omega_{q})t]\sin(\omega_{\text{LO}}t) \nonumber \\ &=\frac{1}{2}[A_{i}(f_{i})\sin(\omega_{c}+\omega_{\text{LO}}-\omega_{i})t-A_{i}(f_{i})\sin(\omega_{c}-\omega_{\text{LO}}-\omega_{i})t \nonumber \\ &\quad +A_{q}(f_{q})\cos(\omega_{c}-\omega_{\text{LO}}-\omega_{q})t-A_{q}(f_{q})\cos(\omega_{c}+\omega_{\text{LO}}-\omega_{q})t \nonumber \\ &\quad -A_{i}(f_{i})\sin(\omega_{c}+\omega_{\text{LO}}+\omega_{i})t+A_{i}(f_{i})\sin(\omega_{c}-\omega_{\text{LO}}+\omega_{i})t \nonumber \\ \label{eq:1} &\quad -A_{q}(f_{q})\cos(\omega_{c}-\omega_{\text{LO}}+\omega_{q})t+A_{q}(f_{q})\cos(\omega_{c}+\omega_{\text{LO}}+\omega_{q})t]\end{align} \]

\(\eqref{eq:1}\)La ecuación incluye términos de frecuencia intermedia centrados en\(\omega_{c}−\omega_{\text{LO}}\) y términos de alta frecuencia centrados en\(\omega_{c}+\omega_{\text{LO}}\). Estos términos de alta frecuencia se pueden eliminar a través del filtrado de paso bajo dejando la señal recibida filtrada de paso bajo

\[\begin{align}i_{\text{IF}}(t)&=\frac{1}{2}[-A_{i}(f_{i})\sin(\omega_{c}-\omega_{\text{LO}}-\omega_{i})t+A_{q}(f_{q})\cos(\omega_{c}-\omega_{\text{LO}}-\omega_{q})t \nonumber \\ &\quad +A_{i}(f_{i})\sin(\omega_{c}-\omega_{\text{LO}}+\omega_{i})t-A_{q}(f_{q})\cos(\omega_{c}-\omega_{\text{LO}}+\omega_{q})t]\nonumber \\ &=\frac{1}{2}A_{i}(f_{i})[-\sin(\omega_{c}-\omega_{\text{LO}}-\omega_{i})t+\sin(\omega_{c}-\omega_{\text{LO}}+\omega_{i})t]\nonumber \\ &\quad +\frac{1}{2}A_{q}(f_{q})[\cos(\omega_{c}-\omega_{\text{LO}}-\omega_{q})t-\cos(\omega_{c}-\omega_{\text{LO}}+\omega_{q})t] \nonumber \\ &=\frac{1}{2}A_{i}(f_{i})[\sin(\omega_{i}-\omega_{c}+\omega_{\text{LO}})t+\sin(\omega_{i}+\omega_{c}-\omega_{\text{LO}})t] \nonumber \\ \label{eq:2} &\quad +\frac{1}{2}A_{q}(f_{q})[\cos(\omega_{q}-\omega_{c}+\omega_{\text{LO}})t-\cos(\omega_{q}+\omega_{c}-\omega_{\text{LO}})t]\end{align} \]

y esta es una señal DSB-SC con una frecuencia portadora\(f_{c} − f_{\text{LO}}\). La ubicación de\(i_{\text{IF}}\) se muestra en la Figura\(\PageIndex{1}\) y su espectro es el espectro medio en la parte inferior de la figura. Por supuesto, la ecuación\(\eqref{eq:2}\) es una señal discreta y el espectro muestra una señal de ancho de banda finito que describe\(i_{\text{IF}}(t)\) sobre el rango de\(f_{i}\) componentes. (Es decir, la suma lineal de\(i_{\text{IF}}(t)\) en Ecuación\(\eqref{eq:2}\) para todos los\(f_{i}\) componentes.)

Demodulación de una etapa con\(f_{\text{LO}}=f_{c}\)

La señal IF,\(i_{\text{IF}}(t)\) se mezcla entonces con el LO IF con frecuencia de radián\(\omega_{\text{LO, IF}}t = \omega_{c}t−\omega_{\text{LO}}t+\phi_{i}\) produciendo la señal de banda base recuperada del canal I

\[\begin{align} i_{\text{BB}}(t)&=\frac{1}{2}A_{i}(f_{i})[\sin(\omega_{i}t+\phi_{i})+\sin(\omega_{i}t-\phi_{i})] \nonumber \\ \label{eq:3}&\quad +\frac{1}{2}A_{q}(f_{q})[\cos(\omega_{q}t+\phi_{i})-\cos(\omega_{q}t-\phi_{i})]\end{align} \]

Entonces si\(\phi_{i} = 0\), que es cuando la fase de la señal at\(f_{\text{LO, IF}}\) ha sido recuperada correctamente, la señal de banda base demodulada para el canal I es

\[\label{eq:4}i_{\text{BB}}(t)=A_{i}(f_{i})\sin(\omega_{i}t) \]

Demodulación de dos etapas\(f_{\text{LO}}<f_{c}\)

En un demodulador SDR hay demodulación de dos etapas con una etapa analógica seguida de una etapa digital y esto es lo que se muestra en la Figura\(\PageIndex{1}\). La etapa analógica, que produce\(i_{\text{IF}}(t)\) en Ecuación\(\eqref{eq:2}\), se encuentra en un chip comúnmente conocido como el chip de módem RF. La segunda etapa suele estar en un chip separado llamado chip de procesamiento de banda base. Una implementación de un receptor SDR utiliza un LO analógico ajustado en pasos de frecuencia discretos y, con\(f_{\text{LO}} < f_{c}\) la señal convertida a la baja resultante\(i_{\text{IF}}(t)\) es una señal DSB-SC con una portadora en\(f_{c} − f_{\text{LO}}\), ver el espectro medio en la parte inferior de la Figura\(\PageIndex{1}\). Una segunda etapa de demodulación en cuadratura opera\(i_{\text{IF}}\). La\(i_{\text{IF}}\) señal a veces se llama señal de banda base si el foco está en el chip del módem RF.

La señal intermedia\(i_{\text{IF}}(t)\) en la ecuación\(\eqref{eq:3}\) se mezcla con una señal portadora IF a la frecuencia de la\(f_{\text{LO, IF}}\) siguiente manera

\[\begin{align} i_{\text{BB}}'(t)&=\left\{\frac{1}{2}A_{i}(f_{i})[\sin(\omega_{i}-\omega_{c}+\omega_{\text{LO}})t+\sin(\omega_{i}+\omega_{c}-\omega_{\text{LO}})t] \right.\nonumber \\ &\quad +\frac{1}{2}A_{q}(f_{q})[\cos(\omega_{q}-\omega_{c}+\omega_{\text{LO}})t-\cos(\omega_{q}+\omega_{c}-\omega_{\text{LO}})t]\left.\right\} \nonumber \\ \label{eq:5} &\quad\times\cos(\omega_{\text{LO, IF}})t \end{align} \]

El espectro de esta señal se muestra en la parte inferior derecha de la Figura\(\PageIndex{1}\) como el espectro inmediatamente adyacente a DC.

La frecuencia LO intermedia se\(f_{\text{LO, IF}}\) puede ajustar con ajuste fino para\(f_{\text{LO, IF}} = f_{c} − f_{\text{LO}}\) que produzca una señal de banda base\(i_{\text{BB}}′(t)\). La recuperación del portador entonces se convierte en el proceso de determinar la fase sincronizada\(f_{\text{LO, IF}}\) que es solo la\(f_{c}\) frecuencia compensada por el valor numérico de\(f_{\text{LO}}\). (Tenga en cuenta que\(\omega_{c} − \omega_{\text{LO}} −\omega_{\text{LO, IF}} = 0,\: −\omega_{c} + \omega_{\text{LO}} +\omega_{\text{LO, IF}} = 0,\: \omega_{c} − \omega_{\text{LO}} + \omega_{\text{LO, IF}} = 2\omega_{\text{LO, IF}}\), y\(−\omega_{c} + \omega_{\text{LO}} − \omega_{\text{LO, IF}} = −2\omega_{c,\text{ IF}}\). La señal de banda base del canal I es entonces

\[\begin{align} i_{\text{BB}}'(t)&=i_{\text{IF}}'(t)\cos(\omega_{\text{LO, IF}}t) \nonumber \\ &=G_{L}\left\{\frac{1}{2}A_{i}(f_{i})[\sin(\omega_{i}-\omega_{c}+\omega_{\text{LO}})t+\sin(\omega_{i}+\omega_{c}-\omega_{\text{LO}})t]\right.\nonumber \\ &\quad+\frac{1}{2}A_{q}(f_{q})[\cos(\omega_{q}-\omega_{c}+\omega_{\text{LO}})t-\cos(\omega_{q}+\omega_{c}-\omega_{\text{LO}})t]\left.\right\} \nonumber \\ &\quad\times\cos(\omega_{\text{LO, IF}}t)\nonumber \\ &=\frac{1}{2}G_{L}A_{i}(f_{i})[\sin(\omega_{i}+0)t+\sin(\omega_{i}-2\omega_{\text{LO, IF}})t\nonumber \\ &\quad+\sin(\omega_{i}+2\omega_{\text{LO, IF}})t+\sin(\omega_{i}+0)t]\nonumber \\ &\quad +\frac{1}{2}G_{L}A_{q}(f_{q})[+\cos(\omega_{q}-2\omega_{\text{LO, IF}})t+\cos(\omega_{q}+0)t\nonumber \\ \label{eq:6} &\quad -\cos(\omega_{q}+0)t-\cos(\omega_{q}+2\omega_{\text{LO, IF}})t]\end{align} \]

Después del filtrado paso bajo (en el DSP) para eliminar componentes centrados en\(±2\omega_{\text{LO, IF}}\)

\[\label{eq:7}i_{\text{BB}}(t)=G_{L}A_{i}(f_{i})\sin(\omega_{i}t) \]

Esta es la señal final deseada y su espectro se muestra como el recuadro en la mitad derecha de la Figura\(\PageIndex{1}\) (entre los dos decodificadores). Este análisis se ha realizado con un solo tono para el canal I pero por extensión esto se mantiene para la señal real del canal I. El muestreo\(i_{\text{BB}}(t)\) en las garrapatas de reloj produce la secuencia de símbolos que se transmitieron que después de la decodificación produce el flujo de bits\(I_{k}\).

3.12.2 Demodulación del\(Q\) Componente

La demodulación del canal Q procede de manera similar. El componente de cuadratura-fase se desmodula de manera similar excepto que la fase de las señales LO difieren en\(90^{\circ}\). Si la señal transmitida es la señal DSB-SC\(s(t)\) con portadora\(f_{c}\) en la Ecuación (3.9.1) (y reemplazada\(\omega_{\text{LO}}\) por\(f_{c}\)) y con una frecuencia LO del receptor\(f_{\text{LO}}\), la señal desmodulada en fase es

\[\begin{align} q_{\text{IF}}'(t)&=G_{L}s(t)\sin(\omega_{\text{LO}}t-\pi /2)\nonumber \\ &=-s(t)\cos(\omega_{\text{LO}}t)\nonumber \\ &=-\frac{1}{2}[A_{i}(f_{i})\cos(\omega_{c}-\omega_{i})t+A_{q}(f_{q})\sin(\omega_{c}-\omega_{q})t \nonumber \\ &\quad -A_{i}(f_{i})\cos(\omega_{c}+\omega_{i})t-A_{q}(f_{q})\sin(\omega_{c}+\omega_{q})t]\cos(\omega_{\text{LO}}t) \nonumber \\ &=-\frac{1}{2}\{A_{i}(f_{i})\cos(\omega_{c}+\omega_{\text{LO}}-\omega_{i})t+A_{i}(f_{i})\cos(\omega_{c}-\omega_{\text{LO}}-\omega_{i})t\nonumber \\ &\quad +A_{q}(f_{q})\sin(\omega_{c}-\omega_{\text{LO}}-\omega_{q})t+A_{q}(f_{q})\sin(\omega_{c}+\omega_{\text{LO}}-\omega_{q})t\nonumber \\ &\quad -A_{i}(f_{i})\cos(\omega_{c}+\omega_{\text{LO}}+\omega_{i})t-A_{i}(f_{i})\cos(\omega_{c}-\omega_{\text{LO}}+\omega_{i})t\nonumber \\ \label{eq:8} &\quad -A_{q}(f{q})\sin(\omega_{c}-\omega_{\text{LO}}+\omega_{q})t+A_{q}(f_{q})\sin(\omega_{c}+\omega_{\text{LO}}+\omega_{q})t\}\end{align} \]

Esto incluye términos de frecuencia intermedia centrados en\(\omega_{c} − \omega_{\text{LO}}\) y términos de alta frecuencia centrados en\(\omega_{c} + \omega_{\text{LO}}\). Estos términos de alta frecuencia se pueden eliminar a través del filtrado de paso bajo dejando la señal del receptor filtrada de paso bajo

\[\begin{align} q_{\text{IF}}(t)&=-\frac{1}{2}[A_{i}(f_{i})\cos(\omega_{c}-\omega_{\text{LO}}-\omega_{i})t+A_{q}(f_{q})\sin(\omega_{c}-\omega_{\text{LO}}-\omega_{q})t\nonumber \\ &\quad -A_{i}(f_{i})\cos(\omega_{c}-\omega_{\text{LO}}+\omega_{i})t-A_{q}(f_{q})\sin(\omega_{c}-\omega_{\text{LO}}+\omega_{q})t]\nonumber \\ &=\frac{1}{2}A_{i}(f_{i})[-\cos(\omega_{c}-\omega_{\text{LO}}-\omega_{i})t+\cos(\omega_{c}-\omega_{\text{LO}}+\omega_{i})t]\nonumber \\ &\quad+\frac{1}{2} A_{q}(f_{q}) [− \sin(\omega_{c} − \omega_{\text{LO}} − \omega_{q})t + \sin(\omega_{c} − \omega_{\text{LO}} + \omega_{q})t]\nonumber \\ & = \frac{1}{2}A_{i}(f_{i}) [− \cos(\omega_{i} − \omega_{c} + \omega_{\text{LO}})t + \cos(\omega_{i} + \omega_{c} − \omega_{\text{LO}})t] \nonumber \\ \label{eq:9}&\quad +\frac{1}{2}A_{q}(f_{q}) [\sin(\omega_{q} − \omega_{c} + \omega_{\text{LO}})t + \sin(\omega_{q} + \omega_{c} − \omega_{\text{LO}})t] \end{align} \]

Demodulación de una etapa con\(f_{\text{LO}}=f_{c}\)

Si la frecuencia LO es igual a la frecuencia portadora pero hay un desplazamiento de\(\phi_{i}\) modo que\(\omega_{\text{LO}}t = \omega_{c}t + \phi_{i}\), entonces la señal de banda base recuperada es

\[\begin{align}q_{\text{BB}}(t)&=\frac{1}{2}A_{i}(f_{i})[-\cos(\omega_{i}t+\phi_{i})+\cos(\omega_{i}t-\phi_{i})]\nonumber \\ \label{eq:10}&=\quad +\frac{1}{2}A_{q}(f_{q})[\sin(\omega_{q}t+\phi_{i})+\sin(\omega_{q}t-\phi_{i})]\end{align} \]

Entonces, si\(\phi_{i} = 0\) la señal de banda base demodulada para el canal I es

\[\label{eq:11}q_{\text{BB}}'(t)=A_{q}(f_{q})\sin(\omega_{q}t) \]

Demodulación de dos etapas\(f_{\text{LO}}<f_{c}\)

Cuando\(q_{\text{IF}}(t)\) en Ecuación\(\eqref{eq:3}\) se mezcla con una señal IF LO a frecuencia,\(f_{\text{LO, IF}}\) la señal resultante es

\[\begin{align}q_{\text{BB}}'(t)&=\left\{\frac{1}{2}A_{i}(f_{i})[\sin(\omega_{i}-\omega_{c}+\omega_{\text{LO}})t+\sin(\omega_{i}+\omega_{c}-\omega_{\text{LO}})t]\right. \nonumber \\ &\quad +\frac{1}{2}A_{q}(f_{q})[\cos(\omega_{q}-\omega_{c}+\omega_{\text{LO}})t-\cos(\omega_{q}+\omega_{c}-\omega_{\text{LO}})t]\left.\right\}\nonumber \\ \label{eq:12} &\quad\times\cos(\omega_{\text{LO, IF}})t\end{align} \]

La frecuencia LO intermedia se\(f_{\text{LO, IF}}\) puede ajustar con ajuste fino para\(f_{\text{LO, IF}} = f_{c} − f_{\text{LO}}\) que produzca una señal de banda base\(q_{\text{BB}}(t)\). (Tenga en cuenta que\(\omega_{c} −\omega_{\text{LO}} −\omega_{\text{LO, IF}} = 0,\: −\omega_{c} +\omega_{\text{LO}} +ω_{\text{LO, IF}} = 0,\: \omega_{c}−\omega_{\text{LO}} +\omega_{\text{LO, IF}} = 2\omega_{\text{LO, IF}},\) y\(−\omega_{c} + \omega_{\text{LO}} − \omega_{\text{LO, IF}} = −2\omega_{\text{LO, IF}}\). La señal de banda base del canal Q es entonces

\[\begin{align} q_{\text{BB}}'(t)&=q_{\text{IF}}(t)\cos(\omega_{\text{LO, IF}}t) \nonumber \\&=G_{L}\left\{\frac{1}{2}A_{i}(f_{i})[-\cos(\omega_{i}-\omega_{c}+\omega_{\text{LO}})t+\cos(\omega_{i}+\omega_{c}-\omega_{\text{LO}})t]\right. \nonumber \\ &\quad\frac{1}{2}A_{q}(f_{q})[\sin(\omega_{q}-\omega_{c}+\omega_{\text{LO}})t+\sin(\omega_{q}+\omega_{c}-\omega_{\text{LO}})t]\left.\right\} \nonumber \\ &\quad\times\cos(\omega_{\text{LO, IF}}t)\nonumber \\ &=\frac{1}{2}G_{L}A_{i}(f_{i})[-\cos(\omega_{i}+0)t+\cos(\omega_{i}-2\omega_{\text{LO, IF}})t \nonumber \\ &\quad +\cos(\omega_{i}+2\omega_{\text{LO, IF}})t+\cos(\omega_{i}+0)t\nonumber \\ &\quad +\frac{1}{2}G_{L}A_{q}(f_{q})[\sin(\omega_{q}-2\omega_{\text{LO, IF}})t+\sin(\omega_{q}+0)t\nonumber \\ \label{eq:13} &\quad -\sin(\omega_{q}+2\omega_{\text{LO, IF}})t-\cos(\omega_{q}+0)t]\end{align} \]

Después del filtrado paso bajo (en el DSP) para eliminar componentes centrados en\(±2\omega_{\text{LO, IF}}\)

\[\label{eq:14}q_{\text{BB}}(t)=G_{L}A_{q}(f_{q})\cos(\omega_{q}t) \]

Esto se puede comparar con la señal original en cuadratura que condujo a la señal modulada DSB-SC\(s(t)\). El componente de\(f_{q}\) frecuencia de\(q(t)\) fue\(A_{q}(f_{q})\sin(\omega_{q}t)\). Así es necesario cambiar la fase de\(q_{\text{BB}}(t)\) para obtener la\(q(t)\) señal original:

\[\begin{align}q_{\text{BB}}(t)\:\text{(phase shifted by }90^{\circ})&=G_{L}A_{q}(f_{q})\cos(\omega_{q}t-\pi /2)q(t)\nonumber \\ \label{eq:15}&=G_{L}A_{q}(f_{q})\sin(\omega_{q}t)\end{align} \]

y esto se puede implementar usando una transformada de Hilbert tal como se hizo en el transmisor SDR.