2.6: Estabilidad del amplificador

Existe el potencial para que un amplificador sea inestable y oscile. Generalmente no se trata de una oscilación constante con amplitud y frecuencia fijas, sino de una respuesta caótica. El diseño del oscilador no es tan sencillo como diseñar un amplificador inestable, si tan solo uno pudiera tener tanta suerte. No hay una métrica simple que indique si un amplificador será estable o no. En el peor de los casos un transistor oscilará sin importar lo que se haga a la circuitería externa [10]. Un fabricante no podría vender dicho transistor y no sería un componente útil en un proceso integrado monolítico. Por lo que no es de extrañar que los amplificadores estables puedan diseñarse utilizando transistores disponibles. Para el análisis de estabilidad, el dispositivo activo en un amplificador lineal a menudo puede tratarse como un puerto de dos (ver Figura 2.5.6 (a)).

Las consideraciones de estabilidad afectan la ganancia máxima (estable) que se puede lograr y la facilidad de diseño. Si la ganancia máxima estable es demasiado baja, entonces es necesario seleccionar otro transistor. Si la ganancia especificada está cerca de la ganancia máxima estable, entonces el diseño será un desafío, especialmente para anchos de banda más amplios. Entonces el esfuerzo de diseño aumenta con transistores más simples (y por lo tanto más baratos). La experiencia es la mejor guía para hacer esta compensación.

Hay muchas maneras de ver la estabilidad. En el dominio del tiempo la inestabilidad se manifiesta como el crecimiento de las señales a lo largo del tiempo independientemente del nivel de la señal de entrada. Sin embargo, es más eficiente analizar y diseñar circuitos de RF y microondas en el dominio de la frecuencia, por lo que la estabilidad debe evaluarse también en el dominio de la frecuencia. Las muchas técnicas de dominio de frecuencia disponibles para evaluar la estabilidad varían según el nivel de cobertura y la facilidad con la que se pueden aplicar. La técnica más simple y más fácil de aplicar se basa en el análisis de dos puertos, lo que lleva a métricas de estabilidad basadas en\(S\) parámetros de dos puertos y al concepto de regiones (llamadas círculos) de estabilidad en un gráfico de Smith y una técnica más general es el análisis de estabilidad Nyquist. Estos se consideran a continuación.

2.6.1 Análisis de estabilidad de dos puertos

El análisis de estabilidad debe aplicarse a los dos puertos más internos que contienen el dispositivo activo y cualquier red de retroalimentación. Si el puerto más interno de dos (incluyendo cualquier retroalimentación) es incondicionalmente estable, entonces el amplificador en el que está incrustado será estable. Así, existe un proceso de selección natural de manera que los transistores disponibles tienden a no sufrir inestabilidades internas.

La oscilación se iniciará si las señales reflejadas en el puerto de entrada aumentan en amplitud a medida que la señal se refleja primero desde la fuente\(\Gamma_{S}\), y luego desde el puerto de entrada. Es decir, si

\[\label{eq:1}|\Gamma_{S}\Gamma_{\text{IN}}|>1 \]

el amplificador será potencialmente inestable en la entrada. Que sea o no realmente inestable dependerá de las fases de\(\Gamma_{S}\) y\(\Gamma_{\text{IN}}\). Esta situación se muestra en el gráfico de flujo de señal de la Figura 2.5.6 (b), donde la oscilación es iniciada por ruido. De manera similar, la oscilación ocurrirá si múltiples reflexiones entre la salida y la carga se construyen en amplitud. Es decir, si

\[\label{eq:2}|\Gamma_{L}\Gamma_{\text{OUT}}|>1 \]

con la oscilación iniciada por el ruido como se muestra en la Figura 2.5.6 (c). Ahora

\[\label{eq:3}|\Gamma_{\text{IN}}|=\left|S_{11}+\frac{S_{12}S_{21}\Gamma_{L}}{1-S_{22}\Gamma_{L}}\right| \]

y

\[\label{eq:4}|\Gamma_{\text{OUT}}|=\left|S_{22}+\frac{S_{12}S_{21}\Gamma_{S}}{1-S_{11}\Gamma_{S}}\right| \]

Combinando ecuaciones\(\eqref{eq:1}\) —\(\eqref{eq:4}\), el amplificador será inestable si

\[\label{eq:5}|\Gamma_{S}\Gamma_{\text{IN}}|=\left|\Gamma_{S}S_{11}+\frac{S_{12}S_{21}\Gamma_{S}\Gamma_{L}}{1-S_{22}\Gamma_{L}}\right|>1 \]

o

\[\label{eq:6}|\Gamma_{L}\Gamma_{\text{OUT}}|=\left|\Gamma_{L}S_{22}+\frac{S_{12}S_{21}\Gamma_{S}\Gamma_{L}}{1-S_{11}\Gamma_{S}}\right|>1 \]

El acoplamiento\(\Gamma_{S}\) y\(\Gamma_{L}\) dificulta el diseño independiente de las redes de coincidencia de entrada y salida. Es mucho más conveniente considerar la situación incondicionalmente estable en la que la entrada es estable sin importar cuál sea la red de coincidencia de carga y salida presente, y la salida es estable sin importar cuál sea la fuente y la red de coincidencia de entrada presente. Como primera etapa en el diseño, un amplificador lineal está diseñado para una estabilidad incondicional. El espacio de diseño es mayor si la prueba más rigurosa de estabilidad, plasmada en Ecuaciones\(\eqref{eq:5}\) y\(\eqref{eq:6}\), se utiliza para determinar la estabilidad. Sin embargo, la ventaja (es decir, un espacio de diseño más grande) suele ser pequeña.

Si la fuente y la carga son pasivas,\(|\Gamma_{L}| < 1\) entonces\(|\Gamma_{S}| < 1\) y para que las oscilaciones se acumulen si

\[\label{eq:7}|\Gamma_{\text{IN}}|>1\quad\text{and}\quad |\Gamma_{\text{OUT}}|>1 \]

Para garantizar la estabilidad para todas las terminaciones pasivas de fuente y carga (es decir, estabilidad incondicional), entonces

\[\label{eq:8}|\Gamma_{\text{IN}}|<1\quad\text{and}\quad |\Gamma_{\text{OUT}}|<1 \]

Los amplificadores a menudo se realizan como etapas mediante las cuales una etapa de amplificador alimenta a otra. Esto complica el análisis de estabilidad, ya que es posible\(\Gamma_{S}\) y\(\Gamma_{L}\) ser más que la unidad. Si\(\Gamma_{S}\) y\(\Gamma_{L}\) son ambos menores que uno para múltiples etapas de amplificador, entonces se puede usar la estabilidad del amplificador que se describe aquí.

Para que los criterios de estabilidad sean utilizados en el diseño deben ser puestos en términos de los parámetros de dispersión del dispositivo activo. Existen dos criterios de estabilidad adecuados comúnmente utilizados, el\(k\) factor -factor y el\(\mu\) -factor, que ahora serán considerados.

2.6.2 Estabilidad incondicional: Círculos de Estabilidad de Dos Puertos

El coeficiente de reflexión de entrada de un dispositivo activo está determinado por los\(S\) parámetros del dispositivo y la carga:

\[\label{eq:9}\Gamma_{\text{IN}}=S_{11}+\frac{S_{12}S_{21}\Gamma_{L}}{1-S_{22}\Gamma_{L}} \]

y así para la estabilidad (para\(|\Gamma_{S}| \leq 1\))

\[\label{eq:10}|\Gamma_{\text{IN}}|=\left|S_{11}+\frac{S_{12}S_{21}\Gamma_{L}}{1-S_{22}\Gamma_{L}}\right|<1 \]

De igual manera, considerando la salida del dispositivo activo, para la estabilidad (con\(|\Gamma_{L}|\leq 1\)),

\[\label{eq:11}|\Gamma_{\text{OUT}}|=\left|S_{22}+\frac{S_{12}S_{21}\Gamma_{S}}{1-S_{11}\Gamma_{S}}\right|<1 \]

Ecuaciones\(\eqref{eq:10}\) y\(\eqref{eq:11}\) deben sostenerse para todos

\[\label{eq:12}|\Gamma_{S}|\leq 1\quad\text{and}\quad |\Gamma_{L}|\leq 1 \]

Cuando el activo es unilateral,\(S_{12} = 0\), y Ecuaciones\(\eqref{eq:10}\) y\(\eqref{eq:11}\) simplificar al requisito de que\(|S_{11}| < 1\) y\(|S_{22}| < 1\). De lo contrario, dado un dispositivo, habrá un límite en los valores de\(\Gamma_{S}\) y\(\Gamma_{L}\) eso asegurará la estabilidad. Los criterios de estabilidad están en términos de las magnitudes de los números complejos, y esto se sabe para especificar círculos en el plano complejo. El siguiente desarrollo conducirá a que el centro y el radio definan los círculos de estabilidad que definen los límites entre regiones estables y potencialmente inestables.

Para\(|\Gamma_{\text{IN}}| = 1\), el círculo de estabilidad de salida se define por

\[\label{eq:13}\left|S_{11}+\frac{S_{12}S_{21}\Gamma_{L}}{1-S_{22}\Gamma_{L}}\right|=1 \]

El desarrollo que sigue pone esto en la forma estándar para un círculo, es decir, en forma de

\[\label{eq:14}|\Gamma_{L}-c|=r \]

donde\(c\) es un número complejo y define el centro del círculo en una gráfica de coeficiente de reflexión, y\(r\) es un número real y es el radio del círculo. Este círculo define el límite entre los valores estables y potencialmente inestables de\(\Gamma_{L}\). Ahora la ecuación se\(\eqref{eq:13}\) puede reescribir como

\[\label{eq:15}|S_{11}-(S_{11}S_{22}-S_{12}S_{21})\Gamma_{L}|=|1-S_{22}\Gamma_{L}| \]

que incluye el determinante,\(\Delta\), de la matriz de parámetros de dispersión. Con

\[\label{eq:16}\Delta=S_{11}S_{22}-S_{12}S_{21} \]

La ecuación\(\eqref{eq:15}\) se convierte

\[\label{eq:17}|S_{11}-\Delta\Gamma_{L}|=|1-S_{22}\Gamma_{L}| \]

Eliminando los signos absolutos multiplicando cada lado por su complejo conjugado y luego reordenando,

\[\begin{align}\label{eq:18}(S_{11}-\Delta\Gamma_{L})(S_{11}-\Delta\Gamma_{L})^{\ast}&=(1-S_{22}\Gamma_{L})(1-S_{22}\Gamma_{L})^{\ast} \\ \label{eq:19}S_{11}S_{11}^{\ast}+\Delta\Delta^{\ast}\Gamma_{L}\Gamma_{L}^{\ast}-(\Delta\Gamma_{L}S_{11}^{\ast}+\Delta^{\ast}\Gamma_{L}^{\ast}S_{11})&=1+S_{22}S_{22}^{\ast}\Gamma_{L}\Gamma_{L}^{\ast} -(S_{22}\Gamma_{L}+S_{22}^{\ast}\Gamma_{L}^{\ast}) \\ \label{eq:20}\left(|S_{22}|^{2}-|\Delta|^{2}\right)\Gamma_{L}\Gamma_{L}^{\ast}-(S_{22}-\Delta S_{11}^{\ast})\Gamma_{L}-(S_{22}^{\ast}-\Delta ^{\ast}S_{11})\Gamma_{L}^{\ast}&=|S_{11}|^{2}-1 \\ \label{eq:21}\Gamma_{L}\Gamma_{L}^{\ast}-\frac{(S_{22}-\Delta S_{11}^{\ast})\Gamma_{L}}{|S_{22}|^{2}-|\Delta |^{2}}-\frac{(S_{22}-\Delta S_{11}^{\ast})^{\ast}\Gamma_{L}^{\ast}}{|S_{22}|^{2}-|\Delta |^{2}}&=\frac{|S_{11}|^{2}-1}{|S_{22}|^{2}-|\Delta |^{2}} \end{align} \]

Añadiendo el mismo término a ambas partes,

\[\begin{align}\Gamma_{L}\Gamma_{L}^{\ast}&-\frac{(S_{22}-\Delta S_{11}^{\ast})\Gamma_{L}}{|S_{22}|^{2}-|\Delta |^{2}}-\frac{(S_{22}-\Delta S_{11}^{\ast})^{\ast}\Gamma_{L}^{\ast}}{|S_{22}|^{2}-|\Delta |^{2}}+\frac{(S_{22}-\Delta S_{11}^{\ast})(S_{22}-\Delta S_{11}^{\ast})^{\ast}}{\left(|S_{22}|^{2}-|\Delta |^{2}\right)^{2}} \nonumber \\ \label{eq:22}&=\frac{|S_{11}|^{2}-1}{|S_{22}|^{2}-|\Delta |^{2}}+\frac{(S_{22}-\Delta S_{11}^{\ast})(S_{22}-\Delta S_{11}^{\ast})^{\ast}}{\left(|S_{22}|^{2}-|\Delta |^{2}\right)^{2}}\end{align} \]

y recopilar términos conduce a la ecuación para un círculo:

\[\label{eq:23}\left|\Gamma_{L}-\frac{S_{22}-\Delta S_{11}^{\ast}}{|S_{22}|^{2}-|\Delta|^{2}}\right|=\left|\frac{S_{12}S_{21}}{|S_{22}|^{2}-|\Delta |^{2}}\right| \]

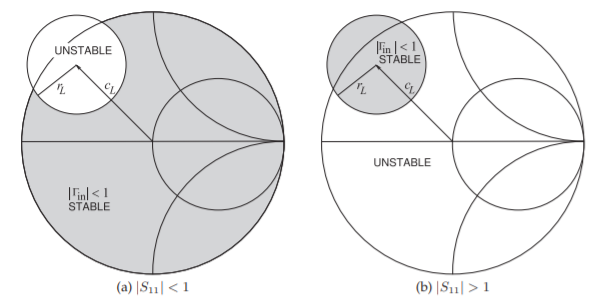
Figura\(\PageIndex{1}\): Círculos de estabilidad de salida en el\(\Gamma_{L}\) plano. Las regiones sombreadas denotan los valores de\(\Gamma_{L}\) que resultarán en estabilidad incondicional en la entrada indicada por\(|\Gamma_{\text{in}}| < 1\).

Esto define un círculo, llamado círculo de estabilidad de salida, en el\(\Gamma_{L}\) plano con centro\(c_{L}\) y radio\(r_{L}\) (el desarrollo de este se da en la Sección 1.A.13) de [7]:

\[\label{eq:24}\text{center : }c_{L}=\frac{(S_{22}-\Delta S_{11}^{\ast})^{\ast}}{|S_{22}|^{2}-|\Delta |^{2}} \]

\[\label{eq:25}\text{radius : }r_{L}=\left|\frac{S_{12}S_{21}}{|S_{22}|^{2}-|\Delta |^{2}}\right| \]

Este círculo se traza en una gráfica de Smith en la Figura\(\PageIndex{1}\) para las dos condiciones\(|S_{11}| < 1\) y\(|S_{11}| > 1\). Cuando\(|S_{11}| < 1\) la región sombreada en la Figura\(\PageIndex{1}\) (a) indica estabilidad incondicional. Es decir, siempre y cuando\(\Gamma_{L}\) se elija para estar en la región sombreada, el coeficiente de reflexión de entrada\(\Gamma_{\text{in}}\),, será menor de uno. No importa cuál sea la impedancia de la fuente, siempre y cuando sea pasiva no habrá oscilación debido a múltiples reflexiones entre la entrada del amplificador y la fuente.

De manera similar, se puede definir un círculo de estabilidad de entrada para\(\Gamma_{S}\), donde

\[\label{eq:26}\text{center : }c_{S}=\frac{(S_{11}-\Delta S_{22}^{\ast})^{\ast}}{|S_{11}|^{2}-|\Delta |^{2}} \]

\[\label{eq:27}\text{radius : }r_{S}=\left|\frac{S_{12}S_{21}}{|S_{11}|^{2}-|\Delta |^{2}}\right| \]

La interpretación de los círculos de estabilidad de entrada, mostrada en la Figura\(\PageIndex{2}\), es similar a la de los círculos de estabilidad de salida.

El criterio de estabilidad proporcionado por los círculos de estabilidad de entrada y salida es muy conservador. Por ejemplo, el círculo de estabilidad de entrada (for\(\Gamma_{S}\)) indica el valor de\(\Gamma_{S}\) que asegurará la estabilidad sin importar qué carga pasiva se presente. Así, los círculos de estabilidad aquí se denominan círculos de estabilidad incondicional. Sin embargo, un amplificador puede ser estable para cargas (o impedancias de fuente) distintas a las que aseguran estabilidad incondicional. El uso de círculos de estabilidad proporciona una buena primera pasada en el diseño de las redes coincidentes entre la fuente real y la carga y el amplificador. Los círculos de estabilidad cambiarán con la frecuencia, por lo que asegurar la estabilidad requiere una amplia visión de frecuencia. Esto se considera en el estudio de caso de diseño de amplificador lineal en la Sección 2.9.

El sombreado se usa comúnmente en publicaciones para indicar el establo y

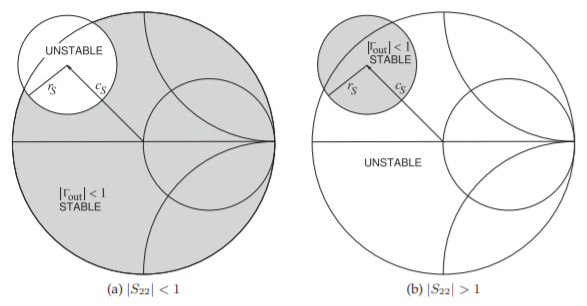
Figura\(\PageIndex{2}\): Círculos de estabilidad de entrada en el\(\Gamma_{S}\) plano. Las regiones sombreadas denotan los valores de\(\Gamma_{S}\) que resultarán en estabilidad incondicional en la salida indicada por\(|\Gamma_{\text{out}}| < 1\).

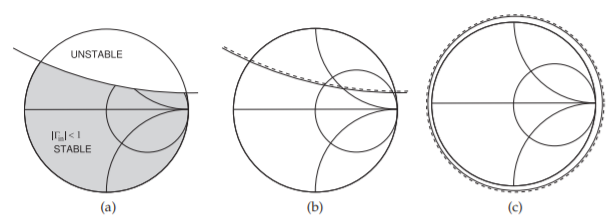
Figura\(\PageIndex{3}\): Círculos de estabilidad: (a) usando la ausencia de sombreado para indicar la región potencialmente inestable; (b) usar una línea discontinua para indicar la misma región potencialmente inestable; y (c) círculo de estabilidad de un dos puertos incondicionalmente estable (diferente).

regiones potencialmente inestables en un gráfico de Smith. Una alternativa comúnmente utilizada por los programas de diseño asistido por computadora de RF y microondas es usar una línea discontinua para indicar el lado del círculo de estabilidad que es potencialmente inestable (ver Figura\(\PageIndex{3}\)). La Figura\(\PageIndex{3}\) (a) usa sombreado para indicar la región potencialmente inestable del gráfico Smith mientras que el círculo de estabilidad en la Figura\(\PageIndex{3}\) (b) indica la región potencialmente inestable usando una línea discontinua. El círculo de estabilidad en la Figura\(\PageIndex{3}\) (c) identifica un puerto de dos puertos que es estable para todas las terminaciones pasivas.

Si un amplificador es incondicionalmente estable, el diseño del amplificador se simplifica considerablemente. Entonces, el diseño de redes coincidentes debe preocuparse por el impacto de las redes coincidentes en la estabilidad. Los análisis detallados de estabilidad se presentan en [11] y [12]. Tenga en cuenta que un amplificador puede ser estable incluso si

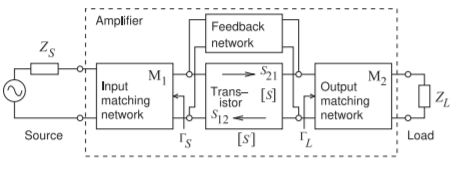
Figura\(\PageIndex{4}\): Configuración general del amplificador.

no es incondicionalmente estable.

2.6.3 Criterio de Estabilidad de Rollet —\(k\) -factor

Nota

Rollet rima con cartera.

El método\(k\) -factor, también conocido como criterio de estabilidad de Rollet [3, 4] es la métrica de estabilidad más utilizada. Se basa en los coeficientes de reflexión de entrada y salida de un dispositivo activo. El amplificador más general se representa en la Figura\(\PageIndex{4}\). Aquí el dispositivo activo tiene parámetros de dispersión

\[\label{eq:28}\mathbf{S}=[S]=\left[\begin{array}{cc}{S_{11}}&{S_{12}}\\{S_{21}}&{S_{22}}\end{array}\right] \]

y, como se va a utilizar mucho, definir el determinante\(\Delta = S_{11}S_{22} − S_{12}S_{21}\). El amplificador general tiene parámetros de dispersión\(\mathbf{S}′\). \(\Gamma_{S}\)es el coeficiente de reflexión del generador y\(\Gamma_{L}\) es el coeficiente de reflexión de la carga. Por estabilidad incondicional,\(|S'_{11}| < 1\) y\(|S'_{22}| < 1\). Si\(|S'_{11}| > 1\) o\(|S'_{22}| > 1\), entonces hay una resistencia negativa y posiblemente podría ocurrir oscilación. La estabilidad incondicional se define como cuándo\(|S'_{11}| < 1\) para todas las cargas pasivas\(\Gamma_{L}\) (es decir,\(|\Gamma_{L}|\leq 1 )\) y\(|S'_{22}| < 1\) para todas las impedancias pasivas de fuente\(\Gamma_{S}\) (es decir,\(|\Gamma_{S}|\leq 1 )\). Estas desigualdades son lo mismo que decir que la parte real de las impedancias de entrada y salida del amplificador son resistencias positivas. Estos requisitos también describen el círculo unitario en una gráfica de Smith. A partir de estas definiciones e ignorando la red de retroalimentación, un factor de estabilidad\(k\),, puede definirse como

\[\label{eq:29}k=\left(\frac{1-|S_{11}|^{2}-|S_{22}|^{2}+|\Delta|^{2}}{2|S_{12}|\: |S_{21}|}\right) \]

donde\(k > 1\) se requiere (pero no suficiente) para una estabilidad incondicional. Esta es la condición de estabilidad Rollet. Lo que se hace aquí es enrollar dos requisitos de estabilidad incondicional (on\(|S′_{11}|\) y\(|S′_{22}|\)) en uno solo. Si\(k\leq 1\), el amplificador puede no ser inestable, pero se requiere un cuidado extra cuando se presenta una carga al amplificador. Si\(k > 1\), el diseño es relativamente sencillo, pero si\(k\) está cerca\(1\) o\(k\leq 1\), el diseño será problemático. Cuanto más cerca esté el diseño de los límites de funcionamiento de un dispositivo, más probable\(k\) será cerca o menor que\(1\). Por ejemplo, el límite podría ser la ganancia máxima estable a la frecuencia de operación prevista.

Se ha demostrado que la estabilidad incondicional está asegurada si

\[\label{eq:30}k=\left(\frac{1-|S_{11}|^{2}-|S_{22}|^{2}+|\Delta |^{2}}{2|S_{12}|\: |S_{21}|}\right)>1 \]

Freq. \((\text{GHz}\))	\(k>1\)	\(|\Delta |<1\)	\(C_{L}\)	\(R_{L}\)	\(C_{S}\)	\(R_{S}\)
\ ((\ text {GHz}\)) ">\(0.5\)	\ (k">1\) ">\(0.15178\)	\ (|\ Delta |<1\) ">\(0.62757\)	\ (C_ {L}\) ">\(1.0388 + \jmath13.5176\)	\ (R_ {L}\) ">\(13.370\)	\ (C_ {S}\) ">\(0.92820 + \jmath0.50682\)	\ (R_ {S}\) ">\(0.22434\)
\ ((\ text {GHz}\)) ">\(1\)	\ (k">1\) ">\(0.24895\)	\ (|\ Delta |<1\) ">\(0.58720\)	\ (C_ {L}\) ">\(0.78679 + \jmath7.26968\)	\ (R_ {L}\) ">\(6.9988\)	\ (C_ {S}\) ">\(0.69258 + \jmath0.96669\)	\ (R_ {S}\) ">\(0.44107\)
\ ((\ text {GHz}\)) ">\(2\)	\ (k">1\) ">\(0.46535\)	\ (|\ Delta |<1\) ">\(0.46821\)	\ (C_ {L}\) ">\(0.73554 + \jmath3.96784\)	\ (R_ {L}\) ">\(3.4718\)	\ (C_ {S}\) ">\(−0.087892 + \jmath1.481129\)	\ (R_ {S}\) ">\(0.72546\)
\ ((\ text {GHz}\)) ">\(3\)	\ (k">1\) ">\(0.67865\)	\ (|\ Delta |<1\) ">\(0.37045\)	\ (C_ {L}\) ">\(0.63608 + \jmath3.17780\)	\ (R_ {L}\) ">\(2.4779\)	\ (C_ {S}\) ">\(−0.86485 + \jmath1.46382\)	\ (R_ {S}\) ">\(0.85475\)
\ ((\ text {GHz}\)) ">\(4\)	\ (k">1\) ">\(0.91943\)	\ (|\ Delta |<1\) ">\(0.29706\)	\ (C_ {L}\) ">\(0.52381 + \jmath2.82057\)	\ (R_ {L}\) ">\(1.9223\)	\ (C_ {S}\) ">\(−1.4232 + \jmath1.2217\)	\ (R_ {S}\) ">\(0.91458\)
\ ((\ text {GHz}\)) ">\(5\)	\ (k">1\) ">\(1.0838\)	\ (|\ Delta |<1\) ">\(0.24365\)	\ (C_ {L}\) ">\(0.32018 + \jmath2.76164\)	\ (R_ {L}\) ">\(1.7276\)	\ (C_ {S}\) ">\(−1.90410 + \jmath0.77291\)	\ (R_ {S}\) ">\(1.0132\)
\ ((\ text {GHz}\)) ">\(6\)	\ (k">1\) ">\(1.1839\)	\ (|\ Delta |<1\) ">\(0.18765\)	\ (C_ {L}\) ">\(0.065264 + \jmath2.679153\)	\ (R_ {L}\) ">\(1.5700\)	\ (C_ {S}\) ">\(−2.182123 + \jmath0.024217\)	\ (R_ {S}\) ">\(1.0885\)
\ ((\ text {GHz}\)) ">\(7\)	\ (k">1\) ">\(1.2846\)	\ (|\ Delta |<1\) ">\(0.14113\)	\ (C_ {L}\) ">\(−0.39857 + \jmath2.97836\)	\ (R_ {L}\) ">\(1.8266\)	\ (C_ {S}\) ">\(−2.06262 − \jmath0.85258\)	\ (R_ {S}\) ">\(1.0885\)
\ ((\ text {GHz}\)) ">\(8\)	\ (k">1\) ">\(1.5225\)	\ (|\ Delta |<1\) ">\(0.092502\)	\ (C_ {L}\) ">\(−0.91418 + \jmath3.21866\)	\ (R_ {L}\) ">\(2.0150\)	\ (C_ {S}\) ">\(−1.5996 − \jmath1.4914\)	\ (R_ {S}\) ">\(0.94750\)
\ ((\ text {GHz}\)) ">\(9\)	\ (k">1\) ">\(1.6448\)	\ (|\ Delta |<1\) ">\(0.056060\)	\ (C_ {L}\) ">\(−1.2526 + \jmath3.0479\)	\ (R_ {L}\) ">\(1.8998\)	\ (C_ {S}\) ">\(−1.1418 − \jmath1.8922\)	\ (R_ {S}\) ">\(0.92223\)
\ ((\ text {GHz}\)) ">\(10\)	\ (k">1\) ">\(1.3151\)	\ (|\ Delta |<1\) ">\(0.072750\)	\ (C_ {L}\) ">\(−1.7681 + \jmath2.6944\)	\ (R_ {L}\) ">\(2.0189\)	\ (C_ {S}\) ">\(−0.54178 − \jmath2.13439\)	\ (R_ {S}\) ">\(1.0468\)
\ ((\ text {GHz}\)) ">\(11\)	\ (k">1\) ">\(1.1043\)	\ (|\ Delta |<1\) ">\(0.11703\)	\ (C_ {L}\) ">\(−2.6666 + \jmath2.4074\)	\ (R_ {L}\) ">\(2.5186\)	\ (C_ {S}\) ">\(0.24025 − \jmath2.02042\)	\ (R_ {S}\) ">\(0.98357\)
\ ((\ text {GHz}\)) ">\(12\)	\ (k">1\) ">\(0.98784\)	\ (|\ Delta |<1\) ">\(0.16159\)	\ (C_ {L}\) ">\(−4.4423 + \jmath2.2978\)	\ (R_ {L}\) ">\(4.0111\)	\ (C_ {S}\) ">\(0.73109 − \jmath1.58120\)	\ (R_ {S}\) ">\(0.74724\)
\ ((\ text {GHz}\)) ">\(13\)	\ (k">1\) ">\(0.92131\)	\ (|\ Delta |<1\) ">\(0.18991\)	\ (C_ {L}\) ">\(−5.9502 + \jmath1.0596\)	\ (R_ {L}\) ">\(5.1100\)	\ (C_ {S}\) ">\(0.96118 − \jmath1.24308\)	\ (R_ {S}\) ">\(0.60117\)
\ ((\ text {GHz}\)) ">\(14\)	\ (k">1\) ">\(0.84098\)	\ (|\ Delta |<1\) ">\(0.21905\)	\ (C_ {L}\) ">\(−5.95467 − \jmath0.75389\)	\ (R_ {L}\) ">\(5.1368\)	\ (C_ {S}\) ">\(1.10689 − \jmath0.97667\)	\ (R_ {S}\) ">\(0.53246\)
\ ((\ text {GHz}\)) ">\(15\)	\ (k">1\) ">\(0.69555\)	\ (|\ Delta |<1\) ">\(0.24320\)	\ (C_ {L}\) ">\(−6.0313 − \jmath1.9645\)	\ (R_ {L}\) ">\(5.6068\)	\ (C_ {S}\) ">\(1.20251 − \jmath0.58617\)	\ (R_ {S}\) ">\(0.43291\)
\ ((\ text {GHz}\)) ">\(16\)	\ (k">1\) ">\(0.63420\)	\ (|\ Delta |<1\) ">\(0.27993\)	\ (C_ {L}\) ">\(−5.7310 − \jmath3.8333\)	\ (R_ {L}\) ">\(6.2171\)	\ (C_ {S}\) ">\(1.26271 − \jmath0.23704\)	\ (R_ {S}\) ">\(0.39187\)
\ ((\ text {GHz}\)) ">\(17\)	\ (k">1\) ">\(0.68792\)	\ (|\ Delta |<1\) ">\(0.32454\)	\ (C_ {L}\) ">\(−3.5163 − \jmath5.6496\)	\ (R_ {L}\) ">\(5.9268\)	\ (C_ {S}\) ">\(1.257206 + \jmath0.087208\)	\ (R_ {S}\) ">\(0.34232\)
\ ((\ text {GHz}\)) ">\(18\)	\ (k">1\) ">\(0.72764\)	\ (|\ Delta |<1\) ">\(0.36197\)	\ (C_ {L}\) ">\(−1.1258 − \jmath5.5386\)	\ (R_ {L}\) ">\(4.8824\)	\ (C_ {S}\) ">\(1.17955 + \jmath0.29932\)	\ (R_ {S}\) ">\(0.27755\)
\ ((\ text {GHz}\)) ">\(19\)	\ (k">1\) ">\(0.89194\)	\ (|\ Delta |<1\) ">\(0.35755\)	\ (C_ {L}\) ">\(0.72551 − \jmath2.82689\)	\ (R_ {L}\) ">\(1.9913\)	\ (C_ {S}\) ">\(1.20751 + \jmath0.32462\)	\ (R_ {S}\) ">\(0.27383\)
\ ((\ text {GHz}\)) ">\(20\)	\ (k">1\) ">\(0.97085\)	\ (|\ Delta |<1\) ">\(0.32318\)	\ (C_ {L}\) ">\(1.1030 − \jmath2.0753\)	\ (R_ {L}\) ">\(1.3671\)	\ (C_ {S}\) ">\(1.19540 + \jmath0.46897\)	\ (R_ {S}\) ">\(0.29068\)
\ ((\ text {GHz}\)) ">\(21\)	\ (k">1\) ">\(0.97475\)	\ (|\ Delta |<1\) ">\(0.28626\)	\ (C_ {L}\) ">\(1.3859 − \jmath1.8451\)	\ (R_ {L}\) ">\(1.3221\)	\ (C_ {S}\) ">\(0.94075 + \jmath0.85514\)	\ (R_ {S}\) ">\(0.27681\)
\ ((\ text {GHz}\)) ">\(22\)	\ (k">1\) ">\(1.1014\)	\ (|\ Delta |<1\) ">\(0.28501\)	\ (C_ {L}\) ">\(2.1696 − \jmath1.1961\)	\ (R_ {L}\) ">\(1.4187\)	\ (C_ {S}\) ">\(0.66834 + \jmath1.07377\)	\ (R_ {S}\) ">\(0.24499\)
\ ((\ text {GHz}\)) ">\(23\)	\ (k">1\) ">\(1.3123\)	\ (|\ Delta |<1\) ">\(0.29397\)	\ (C_ {L}\) ">\(2.35683 − \jmath0.15064\)	\ (R_ {L}\) ">\(1.1976\)	\ (C_ {S}\) ">\(0.51539 + \jmath1.17421\)	\ (R_ {S}\) ">\(0.22605\)
\ ((\ text {GHz}\)) ">\(24\)	\ (k">1\) ">\(1.4714\)	\ (|\ Delta |<1\) ">\(0.28083\)	\ (C_ {L}\) ">\(2.23754 + \jmath0.46967\)	\ (R_ {L}\) ">\(1.0569\)	\ (C_ {S}\) ">\(0.28045 + \jmath1.30061\)	\ (R_ {S}\) ">\(0.24185\)
\ ((\ text {GHz}\)) ">\(25\)	\ (k">1\) ">\(1.4273\)	\ (|\ Delta |<1\) ">\(0.22850\)	\ (C_ {L}\) ">\(2.2473 + \jmath1.2506\)	\ (R_ {L}\) ">\(1.3389\)	\ (C_ {S}\) ">\(0.079906 + \jmath1.412442\)	\ (R_ {S}\) ">\(0.31586\)
\ ((\ text {GHz}\)) ">\(26\)	\ (k">1\) ">\(1.5308\)	\ (|\ Delta |<1\) ">\(0.17235\)	\ (C_ {L}\) ">\(2.6309 + \jmath3.0590\)	\ (R_ {L}\) ">\(2.6671\)	\ (C_ {S}\) ">\(−0.45588 + \jmath1.43292\)	\ (R_ {S}\) ">\(0.36774\)

Cuadro\(\PageIndex{1}\): Parámetros del factor de estabilidad\(|\Delta |\),\(k\) factor y círculo de estabilidad de Rollet del transistor PhemT (en la Tabla 2.3.1). Para que el dispositivo activo sea incondicionalmente estable se deben cumplir dos condiciones:\(k > 1\) y\(|\Delta | < 1\). Las frecuencias en las que el dispositivo es incondicionalmente estable (\(5–11\)y\(22–26\text{ GHz}\)) están en negrita.

combinado con cualquiera de las siguientes condiciones auxiliares [13, 14, 15, 16, 17, 18, 19]:

\[\begin{align}\label{eq:31} B_{1}&=1+|S_{11}|^{2}-|S_{22}|^{2}-|\Delta |^{2}>0 \\ \label{eq:32}B_{2}&=1-|S_{11}|^{2}+|S_{22}|^{2}-|\Delta |^{2}>0 \\ \label{eq:33} |\Delta |&=|S_{11}S_{22}-S_{12}S_{21}|<1 \\ \label{eq:34}C_{1}&=1-|S_{11}|^{2}-|S_{12}S_{21}|>0 \\ \label{eq:35}C_{2}&=1-|S_{22}|^{2}-|S_{12}S_{21}|>0\end{align} \]

Las condiciones en Ecuaciones\(\eqref{eq:31}\) — no\(\eqref{eq:35}\) son independientes, y se puede demostrar que una implica a las otras si\(k > 1\) [13].

Los criterios de estabilidad de Rollet,\(k\) y\(|\Delta |\), se tabulan en la Tabla\(\PageIndex{1}\) para el pHEMT descrito en el Cuadro 2.3.1. El dispositivo es incondicionalmente estable a las frecuencias\(5–11\text{ GHz}\) y\(22–26\text{ GHz}\). Se ve que el dispositivo podría ser potencialmente inestable a frecuencias por debajo\(5\text{ GHz}\) y de\(12\) a\(21\text{ GHz}\). En estas frecuencias, los círculos de estabilidad necesitan ser utilizados en el diseño de redes coincidentes.

Freq \((\text{GHz})\)	\(\mu >1\)	\(B_{1}>0\)	\(B_{2}>0\)	\(|\Delta |<1\)	\(C_{1}>0\)	\(C_{2}>0\)
\ ((\ text {GHz})\) ">\(0.5\)	\ (\ mu “>1\)" >\(0.18785\)	\ (B_ {1} ">0\)" >\(1.1555\)	\ (B_ {2} ">0\)" >\(0.056799\)	\ (|\ Delta |<1\) ">\(0.62757\)	\ (C_ {1} ">0\)" >\(−0.077921\)	\ (C_ {2} ">0\)" >\(0.47143\)
\ ((\ text {GHz})\) ">\(1\)	\ (\ mu “>1\)" >\(0.31338\)	\ (B_ {1} ">0\)" >\(1.1338\)	\ (B_ {2} ">0\)" >\(0.17657\)	\ (|\ Delta |<1\) ">\(0.58720\)	\ (C_ {1} ">0\)" >\(−0.080934\)	\ (C_ {2} ">0\)" >\(0.39770\)
\ ((\ text {GHz})\) ">\(2\)	\ (\ mu “>1\)" >\(0.56362\)	\ (B_ {1} ">0\)" >\(1.1086\)	\ (B_ {2} ">0\)" >\(0.45297\)	\ (|\ Delta |<1\) ">\(0.46821\)	\ (C_ {1} ">0\)" >\(0.065756\)	\ (C_ {2} ">0\)" >\(0.39356\)
\ ((\ text {GHz})\) ">\(3\)	\ (\ mu “>1\)" >\(0.76297\)	\ (B_ {1} ">0\)" >\(1.0884\)	\ (B_ {2} ">0\)" >\(0.63717\)	\ (|\ Delta |<1\) ">\(0.37045\)	\ (C_ {1} ">0\)" >\(0.22398\)	\ (C_ {2} ">0\)" >\(0.44958\)
\ ((\ text {GHz})\) ">\(4\)	\ (\ mu “>1\)" >\(0.94651\)	\ (B_ {1} ">0\)" >\(1.0631\)	\ (B_ {2} ">0\)" >\(0.76039\)	\ (|\ Delta |<1\) ">\(0.29706\)	\ (C_ {1} ">0\)" >\(0.35892\)	\ (C_ {2} ">0\)" >\(0.51029\)
\ ((\ text {GHz})\) ">\(5\)	\ (\ mu “>1\)" >\(1.0526\)	\ (B_ {1} ">0\)" >\(1.0434\)	\ (B_ {2} ">0\)" >\(0.83782\)	\ (|\ Delta |<1\) ">\(0.24365\)	\ (C_ {1} ">0\)" >\(0.44002\)	\ (C_ {2} ">0\)" >\(0.54284\)
\ ((\ text {GHz})\) ">\(6\)	\ (\ mu “>1\)" >\(1.1100\)	\ (B_ {1} ">0\)" >\(1.0341\)	\ (B_ {2} ">0\)" >\(0.89551\)	\ (|\ Delta |<1\) ">\(0.18765\)	\ (C_ {1} ">0\)" >\(0.49297\)	\ (C_ {2} ">0\)" >\(0.56225\)
\ ((\ text {GHz})\) ">\(7\)	\ (\ mu “>1\)" >\(1.1783\)	\ (B_ {1} ">0\)" >\(1.0703\)	\ (B_ {2} ">0\)" >\(0.88992\)	\ (|\ Delta |<1\) ">\(0.14113\)	\ (C_ {1} ">0\)" >\(0.51407\)	\ (C_ {2} ">0\)" >\(0.60424\)
\ ((\ text {GHz})\) ">\(8\)	\ (\ mu “>1\)" >\(1.3310\)	\ (B_ {1} ">0\)" >\(1.1120\)	\ (B_ {2} ">0\)" >\(0.87085\)	\ (|\ Delta |<1\) ">\(0.092502\)	\ (C_ {1} ">0\)" >\(0.54812\)	\ (C_ {2} ">0\)" >\(0.66871\)
\ ((\ text {GHz})\) ">\(9\)	\ (\ mu “>1\)" >\(1.3954\)	\ (B_ {1} ">0\)" >\(1.1104\)	\ (B_ {2} ">0\)" >\(0.88335\)	\ (|\ Delta |<1\) ">\(0.056060\)	\ (C_ {1} ">0\)" >\(0.57284\)	\ (C_ {2} ">0\)" >\(0.68634\)
\ ((\ text {GHz})\) ">\(10\)	\ (\ mu “>1\)" >\(1.2039\)	\ (B_ {1} ">0\)" >\(1.1068\)	\ (B_ {2} ">0\)" >\(0.88259\)	\ (|\ Delta |<1\) ">\(0.072750\)	\ (C_ {1} ">0\)" >\(0.51811\)	\ (C_ {2} ">0\)" >\(0.63023\)
\ ((\ text {GHz})\) ">\(11\)	\ (\ mu “>1\)" >\(1.0739\)	\ (B_ {1} ">0\)" >\(1.1550\)	\ (B_ {2} ">0\)" >\(0.81758\)	\ (|\ Delta |<1\) ">\(0.11703\)	\ (C_ {1} ">0\)" >\(0.43720\)	\ (C_ {2} ">0\)" >\(0.60592\)
\ ((\ text {GHz})\) ">\(12\)	\ (\ mu “>1\)" >\(0.99026\)	\ (B_ {1} ">0\)" >\(1.2715\)	\ (B_ {2} ">0\)" >\(0.67626\)	\ (|\ Delta |<1\) ">\(0.16159\)	\ (C_ {1} ">0\)" >\(0.33481\)	\ (C_ {2} ">0\)" >\(0.63244\)
\ ((\ text {GHz})\) ">\(13\)	\ (\ mu “>1\)" >\(0.93383\)	\ (B_ {1} ">0\)" >\(1.3461\)	\ (B_ {2} ">0\)" >\(0.58173\)	\ (|\ Delta |<1\) ">\(0.18991\)	\ (C_ {1} ">0\)" >\(0.27037\)	\ (C_ {2} ">0\)" >\(0.65257\)
\ ((\ text {GHz})\) ">\(14\)	\ (\ mu “>1\)" >\(0.86542\)	\ (B_ {1} ">0\)" >\(1.3788\)	\ (B_ {2} ">0\)" >\(0.52518\)	\ (|\ Delta |<1\) ">\(0.21905\)	\ (C_ {1} ">0\)" >\(0.22227\)	\ (C_ {2} ">0\)" >\(0.64910\)
\ ((\ text {GHz})\) ">\(15\)	\ (\ mu “>1\)" >\(0.73637\)	\ (B_ {1} ">0\)" >\(1.4578\)	\ (B_ {2} ">0\)" >\(0.42389\)	\ (|\ Delta |<1\) ">\(0.24320\)	\ (C_ {1} ">0\)" >\(0.13811\)	\ (C_ {2} ">0\)" >\(0.65507\)
\ ((\ text {GHz})\) ">\(16\)	\ (\ mu “>1\)" >\(0.67769\)	\ (B_ {1} ">0\)" >\(1.4752\)	\ (B_ {2} ">0\)" >\(0.36811\)	\ (|\ Delta |<1\) ">\(0.27993\)	\ (C_ {1} ">0\)" >\(0.099372\)	\ (C_ {2} ">0\)" >\(0.65290\)
\ ((\ text {GHz})\) ">\(17\)	\ (\ mu “>1\)" >\(0.72762\)	\ (B_ {1} ">0\)" >\(1.4461\)	\ (B_ {2} ">0\)" >\(0.34324\)	\ (|\ Delta |<1\) ">\(0.32454\)	\ (C_ {1} ">0\)" >\(0.10910\)	\ (C_ {2} ">0\)" >\(0.66053\)
\ ((\ text {GHz})\) ">\(18\)	\ (\ mu “>1\)" >\(0.76942\)	\ (B_ {1} ">0\)" >\(1.4300\)	\ (B_ {2} ">0\)" >\(0.30791\)	\ (|\ Delta |<1\) ">\(0.36197\)	\ (C_ {1} ">0\)" >\(0.10899\)	\ (C_ {2} ">0\)" >\(0.67006\)
\ ((\ text {GHz})\) ">\(19\)	\ (\ mu “>1\)" >\(0.92718\)	\ (B_ {1} ">0\)" >\(1.3348\)	\ (B_ {2} ">0\)" >\(0.40953\)	\ (|\ Delta |<1\) ">\(0.35755\)	\ (C_ {1} ">0\)" >\(0.18890\)	\ (C_ {2} ">0\)" >\(0.65152\)
\ ((\ text {GHz})\) ">\(20\)	\ (\ mu “>1\)" >\(0.98311\)	\ (B_ {1} ">0\)" >\(1.2924\)	\ (B_ {2} ">0\)" >\(0.49876\)	\ (|\ Delta |<1\) ">\(0.32318\)	\ (C_ {1} ">0\)" >\(0.24511\)	\ (C_ {2} ">0\)" >\(0.64191\)
\ ((\ text {GHz})\) ">\(21\)	\ (\ mu “>1\)" >\(0.98558\)	\ (B_ {1} ">0\)" >\(1.3331\)	\ (B_ {2} ">0\)" >\(0.50306\)	\ (|\ Delta |<1\) ">\(0.28626\)	\ (C_ {1} ">0\)" >\(0.24786\)	\ (C_ {2} ">0\)" >\(0.66286\)
\ ((\ text {GHz})\) ">\(22\)	\ (\ mu “>1\)" >\(1.0587\)	\ (B_ {1} ">0\)" >\(1.3627\)	\ (B_ {2} ">0\)" >\(0.47486\)	\ (|\ Delta |<1\) ">\(0.28501\)	\ (C_ {1} ">0\)" >\(0.25075\)	\ (C_ {2} ">0\)" >\(0.69466\)
\ ((\ text {GHz})\) ">\(23\)	\ (\ mu “>1\)" >\(1.1641\)	\ (B_ {1} ">0\)" >\(1.3295\)	\ (B_ {2} ">0\)" >\(0.49769\)	\ (|\ Delta |<1\) ">\(0.29397\)	\ (C_ {1} ">0\)" >\(0.28504\)	\ (C_ {2} ">0\)" >\(0.70093\)
\ ((\ text {GHz})\) ">\(24\)	\ (\ mu “>1\)" >\(1.2294\)	\ (B_ {1} ">0\)" >\(1.2872\)	\ (B_ {2} ">0\)" >\(0.55509\)	\ (|\ Delta |<1\) ">\(0.28083\)	\ (C_ {1} ">0\)" >\(0.33166\)	\ (C_ {2} ">0\)" >\(0.69771\)
\ ((\ text {GHz})\) ">\(25\)	\ (\ mu “>1\)" >\(1.2330\)	\ (B_ {1} ">0\)" >\(1.2866\)	\ (B_ {2} ">0\)" >\(0.60899\)	\ (|\ Delta |<1\) ">\(0.22850\)	\ (C_ {1} ">0\)" >\(0.36433\)	\ (C_ {2} ">0\)" >\(0.70313\)
\ ((\ text {GHz})\) ">\(26\)	\ (\ mu “>1\)" >\(1.3676\)	\ (B_ {1} ">0\)" >\(1.3398\)	\ (B_ {2} ">0\)" >\(0.60077\)	\ (|\ Delta |<1\) ">\(0.17235\)	\ (C_ {1} ">0\)" >\(0.38405\)	\ (C_ {2} ">0\)" >\(0.75358\)

Cuadro\(\PageIndex{2}\): Parámetros de estabilidad de Edwards— Sinsky para el transistor pHEMT documentados en la Tabla 2.3.1. Para la estabilidad,\(\mu > 1\). Las frecuencias a las que el dispositivo es incondicionalmente estable están en negrita. El dispositivo es incondicionalmente estable a las frecuencias\(5–11\text{ GHz}\) y\(22–26\text{ GHz}\). Las otras columnas se refieren a Ecuaciones\(\eqref{eq:31}\) —\(\eqref{eq:35}\) y se proporcionan para completar.

2.6.4 Criterio de Estabilidad Edwards-Sinsky —\(\mu\) -factor

El criterio de estabilidad de Rollet\(\eqref{eq:35}\), Ecuaciones\(\eqref{eq:30}\) —, asegura estabilidad incondicional pero no proporciona una medida relativa de estabilidad. Es decir, el\(k\) factor no se puede utilizar para determinar qué tan cerca está un diseño en particular del borde de la estabilidad. No hay capacidad para comparar la estabilidad relativa de diferentes diseños. Edwards y Sinsky [13] desarrollaron una prueba que puede ser utilizada para comparar la estabilidad relativa de diferentes diseños. Esto se denomina criterio de estabilidad\(\mu\) -factor, con estabilidad incondicional teniendo

\[\label{eq:36}\mu=\frac{1-|S_{11}|^{2}}{|S_{22}-S_{11}^{\ast}\Delta |+|S_{21}S_{12}|}>1 \]

Un resultado importante es que un mayor valor de\(\mu\) indica mayor estabilidad. El\(\mu\) factor es una sola cantidad que proporciona una condición suficiente y necesaria para una estabilidad incondicional. Es decir, no importa qué fuente pasiva y carga se presenten (es decir, si\(|\Gamma_{S}|\leq 1\) y\(|\Gamma_{L}|\leq 1\)) entonces el amplificador será estable si\(\mu > 1\). Esto contrasta con el criterio de estabilidad de Rollet en el que se deben cumplir dos condiciones.

Los parámetros de estabilidad Edwards—Sinsky para el transistor PhemT (documentados en la Tabla 2.3.1) se muestran en la Tabla\(\PageIndex{2}\). Las frecuencias incondicionalmente estables de operación son\(5–11\text{ GHz}\) y\(22–26\text{ GHz}\). Estas son las mismas frecuencias incondicionalmente estables determinadas mediante el criterio de estabilidad de Rollet (en la Tabla\(\PageIndex{1}\)). La información adicional disponible con el Edwards—

Figura\(\PageIndex{5}\): Análisis de estabilidad de Nyquist: (a) amplificador de retroalimentación; (b) un bucle con coeficientes de reflexión\(\Gamma_{1}\) y\(\Gamma_{2}\); y (c) una gráfica de estabilidad Nyquist de ganancia de bucle\(G = −\Gamma_{1}\Gamma_{2}\) (con\(H\) conjunto a\(1\)).

El criterio de estabilidad de Sinsky es el que\(\mu\) indica la estabilidad relativa. En Tabla\(\PageIndex{2}\), el transistor es incondicionalmente estable en el\(5–11\text{ GHz}\) rango, y en este rango el dispositivo es más estable entre\(8\) y\(10\text{ GHz}\). En la gama alta, arriba\(22\text{ GHz}\), el dispositivo es cada vez más estable. Se puede esperar que esto continúe ya que los parásitos capacitivos del dispositivo cortocircuitan el dispositivo. (El resultado de la baja impedancia de los condensadores a altas frecuencias es que se generarán voltajes de RF más pequeños para el mismo nivel de accionamiento). Por lo que este transistor hará un muy buen\(8–10\text{ GHz}\) amplificador siempre que se elijan redes de coincidencia adecuadas para asegurar la estabilidad por debajo\(5\text{ GHz}\) y por encima\(11\text{ GHz}\). Tenga en cuenta, sin embargo, que el amplificador se puede utilizar hasta aproximadamente\(20\text{ GHz}\), pero con especial cuidado en el diseño. Por encima de\(20\text{ GHz}\) la ganancia máxima unilateral del transductor es demasiado pequeña para ser útil (ver Cuadro 2.3.3, donde\(G_{TU\text{,max}}\) se tabula para este transistor).

El factor de estabilidad Edwards—Sinsky,\(\mu\), también se llama factor de estabilidad geométrica. Es la distancia desde el centro del gráfico Smith (es decir, el origen de la gráfica polar del\(S\) parámetro) hasta el punto potencialmente inestable más cercano en el plano de origen de entrada. Es decir, es la distancia más corta desde el origen hasta el círculo de estabilidad de entrada, donde un negativo\(\mu\) indica que el círculo de estabilidad abarca el origen de la carta Smith.

Edwards y Sinsky también definieron un parámetro dual,\(\mu ′\) [13]:

\[\label{eq:37}\mu '=\frac{1-|S_{22}|^{2}}{|S_{11}-S_{22}^{\ast}\Delta |+|S_{21}S_{12}|} \]

Esta es la distancia desde el centro de la gráfica Smith (es decir, el origen de la gráfica polar del\(S\) parámetro) hasta el punto potencialmente inestable más cercano en el plano de carga de salida. Es decir, es la distancia más corta desde el origen hasta el círculo de estabilidad de salida. Si\(\mu > 1\) (indicando la posibilidad de inestabilidad de dos puertos), entonces\(\mu′ > 1\) también. Así, para determinar si un puerto de dos puertos es incondicionalmente estable, sólo es necesario considerar uno de ellos. Además,\(\mu\) y a veces\(\mu ′\) se les conoce como los factores de estabilidad geométrica de entrada y salida respectivamente, y a veces simplemente como\(\mu_{1}\) (MU1) y\(\mu_{2}\) (MU2), respectivamente. Calcular ambos\(\mu\) y\(\mu ′\) es útil, ya que esto permite examinar la estabilidad relativa en la entrada y en la salida. \(\PageIndex{3}\)Listas de tablas\(\mu\) y\(\mu ′\) para el transistor PhemT considerado previamente.

2.6.5 Criterio de Estabilidad Nyquist

El criterio de estabilidad Nyquist es la forma más completa de analizar la estabilidad. Se basa en el análisis del sistema de retroalimentación mostrado en la Figura\(\PageIndex{5}\) (a) [20, 21, 22, 23]. La función de transferencia de bucle cerrado es

\[\label{eq:38}T=\frac{G}{1+GH} \]

Freq. \((\text{GHz})\)	\(\mu\)(MU1) (entrada)	\(\mu '\)(MU2) (salida)
\ ((\ text {GHz})\) ">\(0.5\)	\ (\ mu\) (MU1) (entrada) ">\(0.18785\)	\ (\ mu '\) (MU2) (salida) ">\(0.8332\)
\ ((\ text {GHz})\) ">\(1\)	\ (\ mu\) (MU1) (entrada) ">\(0.31338\)	\ (\ mu '\) (MU2) (salida) ">\(0.74811\)
\ ((\ text {GHz})\) ">\(2\)	\ (\ mu\) (MU1) (entrada) ">\(0.56362\)	\ (\ mu '\) (MU2) (salida) ">\(0.75828\)
\ ((\ text {GHz})\) ">\(3\)	\ (\ mu\) (MU1) (entrada) ">\(0.76297\)	\ (\ mu '\) (MU2) (salida) ">\(0.84547\)
\ ((\ text {GHz})\) ">\(4\)	\ (\ mu\) (MU1) (entrada) ">\(0.94651\)	\ (\ mu '\) (MU2) (salida) ">\(0.96112\)
\ ((\ text {GHz})\) ">\(5\)	\ (\ mu\) (MU1) (entrada) ">\(1.05257\)	\ (\ mu '\) (MU2) (salida) ">\(1.04174\)
\ ((\ text {GHz})\) ">\(6\)	\ (\ mu\) (MU1) (entrada) ">\(1.10997\)	\ (\ mu '\) (MU2) (salida) ">\(1.09373\)
\ ((\ text {GHz})\) ">\(7\)	\ (\ mu\) (MU1) (entrada) ">\(1.17828\)	\ (\ mu '\) (MU2) (salida) ">\(1.14339\)
\ ((\ text {GHz})\) ">\(8\)	\ (\ mu\) (MU1) (entrada) ">\(1.33101\)	\ (\ mu '\) (MU2) (salida) ">\(1.23947\)
\ ((\ text {GHz})\) ">\(9\)	\ (\ mu\) (MU1) (entrada) ">\(1.39544\)	\ (\ mu '\) (MU2) (salida) ">\(1.28779\)
\ ((\ text {GHz})\) ">\(10\)	\ (\ mu\) (MU1) (entrada) ">\(1.20387\)	\ (\ mu '\) (MU2) (salida) ">\(1.15528\)
\ ((\ text {GHz})\) ">\(11\)	\ (\ mu\) (MU1) (entrada) ">\(1.07392\)	\ (\ mu '\) (MU2) (salida) ">\(1.05108\)
\ ((\ text {GHz})\) ">\(12\)	\ (\ mu\) (MU1) (entrada) ">\(0.99026\)	\ (\ mu '\) (MU2) (salida) ">\(0.99479\)
\ ((\ text {GHz})\) ">\(13\)	\ (\ mu\) (MU1) (entrada) ">\(0.93383\)	\ (\ mu '\) (MU2) (salida) ">\(0.97018\)
\ ((\ text {GHz})\) ">\(14\)	\ (\ mu\) (MU1) (entrada) ">\(0.86542\)	\ (\ mu '\) (MU2) (salida) ">\(0.94371\)
\ ((\ text {GHz})\) ">\(15\)	\ (\ mu\) (MU1) (entrada) ">\(0.73637\)	\ (\ mu '\) (MU2) (salida) ">\(0.90486\)
\ ((\ text {GHz})\) ">\(16\)	\ (\ mu\) (MU1) (entrada) ">\(0.67769\)	\ (\ mu '\) (MU2) (salida) ">\(0.89289\)
\ ((\ text {GHz})\) ">\(17\)	\ (\ mu\) (MU1) (entrada) ">\(0.72762\)	\ (\ mu '\) (MU2) (salida) ">\(0.91790\)
\ ((\ text {GHz})\) ">\(18\)	\ (\ mu\) (MU1) (entrada) ">\(0.76942\)	\ (\ mu '\) (MU2) (salida) ">\(0.93939\)
\ ((\ text {GHz})\) ">\(19\)	\ (\ mu\) (MU1) (entrada) ">\(0.92718\)	\ (\ mu '\) (MU2) (salida) ">\(0.97655\)
\ ((\ text {GHz})\) ">\(20\)	\ (\ mu\) (MU1) (entrada) ">\(0.98311\)	\ (\ mu '\) (MU2) (salida) ">\(0.99342\)
\ ((\ text {GHz})\) ">\(21\)	\ (\ mu\) (MU1) (entrada) ">\(0.98558\)	\ (\ mu '\) (MU2) (salida) ">\(0.99451\)
\ ((\ text {GHz})\) ">\(22\)	\ (\ mu\) (MU1) (entrada) ">\(1.05874\)	\ (\ mu '\) (MU2) (salida) ">\(1.01979\)
\ ((\ text {GHz})\) ">\(23\)	\ (\ mu\) (MU1) (entrada) ">\(1.16408\)	\ (\ mu '\) (MU2) (salida) ">\(1.05629\)
\ ((\ text {GHz})\) ">\(24\)	\ (\ mu\) (MU1) (entrada) ">\(1.22944\)	\ (\ mu '\) (MU2) (salida) ">\(1.08865\)
\ ((\ text {GHz})\) ">\(25\)	\ (\ mu\) (MU1) (entrada) ">\(1.23297\)	\ (\ mu '\) (MU2) (salida) ">\(1.09884\)
\ ((\ text {GHz})\) ">\(26\)	\ (\ mu\) (MU1) (entrada) ">\(1.36763\)	\ (\ mu '\) (MU2) (salida) ">\(1.13596\)

Tabla\(\PageIndex{3}\): Parámetros de estabilidad Edwards—Sinsky de entrada y salida para el transistor pHEMT documentados en la Tabla 2.3.1. Para la estabilidad,\(\mu > 1\) y\(\mu ′ > 1\). El dispositivo es incondicionalmente estable a las frecuencias\(5–11\text{ GHz}\) y\(22–26\text{ GHz}\).

El sistema de retroalimentación es inestable si la función de transferencia de bucle abierto\(GH = −1\). Por lo general, en el análisis de estabilidad\(H\) se considera\(1\) que es tal que el sistema es inestable si la función de transferencia de bucle abierto\(G = −1\). Relacionando esto con los circuitos de microondas, se considera cada bucle en un gráfico de flujo de señal. Generalmente es suficiente considerar todos los bucles posibles que contienen un par de nodos, como se muestra en la Figura\(\PageIndex{5}\) (b). Lo mejor sería seleccionar el par de nodos en la entrada o salida de un dispositivo activo, ya que seguramente el dispositivo activo va a estar involucrado en la inestabilidad. Por supuesto, existe la posibilidad de que se pierda el par crítico de nodos, lo que es más probable que suceda en un amplificador multietapa. En esa situación se deben considerar individualmente varios pares de nodos. Volviendo a un solo par de nodos, como se muestra en la Figura\(\PageIndex{5}\) (b), aquí la función de transferencia de dominio de frecuencia de bucle abierto es

\[\label{eq:39}G=\Gamma_{1}\Gamma_{2} \]

El criterio de estabilidad Nyquist es que el sistema es inestable si la función de transferencia de bucle abierto\(G\),, trazada en la llanura compleja rodea el\(−1\) punto en una rotación en sentido horario con frecuencia creciente. Los detalles detrás de esto se proporcionan en casi todos los libros sobre sistemas de control lineal (e.g. [20, 21, 22, 23]).

Para asegurar la estabilidad, la gráfica Nyquist, como se llama a la Figura\(\PageIndex{5}\) (c), debe representarse para cada bucle de un sistema. Sin embargo, la experiencia es una buena guía y solo unos pocos bucles necesitan ser considerados en la práctica. También hay métricas como el parámetro de\(S\) sonda (a veces llamado\(G\) sonda) utilizado en los simuladores de circuito de microondas que proporcionan una buena estimación de si

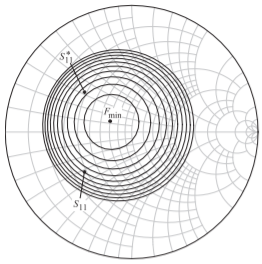
Figura\(\PageIndex{16}\): Circulos de figura de ruido en\(8\text{ GHz}\), trazados en el gráfico Smith de entrada (es decir, en el gráfico\(\Gamma_{S}\) Smith) para el transistor pHEMT documentado en la Tabla 2.3.1. \(F_{\text{min}}\)es\(1.04\text{ dB}\) y los círculos están en\(0.1\text{ dB}\) círculos de manera que el círculo exterior es el locus de\(\Gamma_{S}\) que producirá una figura de ruido de\(2.04\text{ dB}\).

La trama nyquist rodeará el punto [24]. La utilidad de esto es que un elemento SPROBE o GPROBE de dos puertos puede insertarse en un circuito y usarse para proporcionar una medida de estabilidad de Nyquist considerando la ganancia de bucle abierto basada en coeficientes de reflexión que buscan desde cada puerto.

Una técnica similar a la aplicación del criterio de estabilidad Nyquist es crear una gráfica Bode [25]. Sin embargo, esto no es fácil de hacer con muchos circuitos de microondas y no suele usarse.

2.6.6 Resumen

En esta sección se presentaron criterios que pueden ser utilizados para determinar la estabilidad de amplificadores de transistores y de dispositivos activos. Las pruebas de estabilidad deben aplicarse a los dos puertos más internos, específicamente al dispositivo activo, para proporcionar una mayor confianza en el diseño. Se presentaron dos criterios en las formas de FOM para la estabilidad incondicional: el\(k\) -factor y\(\mu\) -factor. El\(k\) factor -que forma parte del criterio de estabilidad incondicional de Rollet, es una prueba de si un dispositivo es incondicionalmente estable o no. No proporciona una medida relativa de estabilidad. El\(\mu\) -factor, derivado de Edwards y Sinsky, es un factor que indica la estabilidad relativa de una red. Los amplificadores estables se pueden diseñar incluso si el amplificador no es incondicionalmente estable. Los círculos de estabilidad ayudan en el diseño de dichos amplificadores. La estabilidad es un tema extenso y el lector está dirigido al análisis de estabilidad en profundidad por parte de Suárez y Quere [12] para mayor información.

También se presentaron dos técnicas gráficas. Los círculos de estabilidad se pueden usar en el diseño para permitir una compensación gráfica de estabilidad, ruido, ganancia y ancho de banda que se muestra en un gráfico de Smith. Es sorprendente lo bien que un diseñador puede hacer el trade-off.