1.5: Propiedades de los Materiales

Propiedades Macroscópicas

Para entender los dispositivos de conversión de energía, necesitamos entender los materiales tanto microscópicamente a escala atómica como macroscópicamente a grandes escalas. Una propiedad macroscópica es una propiedad que se aplica a piezas grandes del material en lugar de piezas de tamaño microscópico.

Una forma de clasificar los materiales es en función de su estado de la materia. Los materiales pueden clasificarse como sólidos, líquidos, gases o plasmas. Un plasma es un gas ionizado. Existen otros estados de la materia más inusuales como los condensados de Bose Einstein, pero no serán discutidos en este libro.

Figura\(\PageIndex{1}\): Ilustración de la estructura atómica cristalina, amorfa y policristalina.

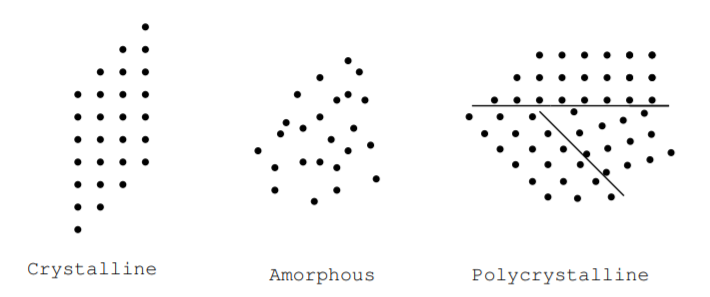
Podemos clasificar adicionalmente los sólidos como cristalinos, policristalinos o amorfos en función de la regularidad de su estructura atómica [9]. La figura\(\PageIndex{1}\) ilustra estos términos. En un cristal, la disposición de los átomos es periódica. Los átomos pueden estar dispuestos en una matriz cúbica, matriz hexagonal, o de alguna otra manera, pero se disponen periódicamente en tres dimensiones. En un material amorfo, la disposición de los átomos no es periódica. El término amorfo significa vítreo. Un material policristalino está compuesto por pequeñas regiones cristalinas. Estas definiciones pueden aplicarse a materiales hechos de elementos individuales o materiales hechos de múltiples elementos. Muchos dispositivos de conversión de energía están hechos de materiales cristalinos, amorfos o policristalinos muy puros. Por ejemplo, el telururo de cadmio amorfo se utiliza para fabricar células solares, y el silicio cristalino se utiliza para fabricar dispositivos de efecto Hall. Muchos materiales, incluyendo tanto el silicio como el dióxido de silicio, se pueden encontrar en estas tres formas a temperatura ambiente. En el silicio cristalino y amorfo, por ejemplo, los átomos de silicio pueden tener el mismo número de vecinos más cercanos, y la densidad de átomos en ambos materiales puede ser la misma, pero no hay un orden de rango medio en el material amorfo. Las propiedades eléctricas de las formas cristalinas, amorfas y policristalinas de un material pueden diferir. Los electrones pueden fluir más fácilmente a través de un material cristalino puro, mientras que es más probable que los electrones se dispersen o absorban a medida que fluyen a través de un material amorfo, materiales cristalinos con impurezas o un material cristalino con defectos cristalinos.

Podemos clasificar adicionalmente los cristales como isotrópicos o anisotrópicos [10, p. 210]. Un cristal es isotrópico si su estructura macroscópica y las propiedades del material son las mismas en cada dirección. Un cristal es anisotrópico si la estructura macroscópica y las propiedades del material son diferentes en diferentes direcciones.

También podemos clasificar los materiales en función de cómo se comportan cuando se aplica un voltaje a través del material [11]. En un conductor, los electrones fluyen fácilmente en presencia de un voltaje aplicado o campo eléctrico. En un aislante, también llamado dieléctrico, los electrones no fluyen en presencia de un voltaje aplicado o campo eléctrico. En presencia de una pequeña tensión externa o campo eléctrico, un semiconductor actúa como aislante, y en presencia de un fuerte voltaje o campo eléctrico, un semiconductor actúa como conductor. Tanto los sólidos como los líquidos pueden ser conductores, y tanto los sólidos como los líquidos pueden ser aislantes. Por ejemplo, el cobre es un conductor sólido mientras que el agua salada es un conductor líquido.

Propiedades microscópicas

La configuración electrónica enumera los niveles de energía ocupados por electrones alrededor de un átomo. La configuración electrónica puede describir átomos neutros o ionizados, y puede describir átomos en el estado de energía más baja o átomos excitados. Por ejemplo, la configuración electrónica de un átomo de aluminio neutro en el estado de energía más bajo es\(1s^{2}2s^{2}2p^{6}3s^{2}3p^{1}\). La configuración electrónica de un\(^{+}\) ion de aluminio Al en el estado de energía más baja es\(1s^{2}2s^{2}2p^{6}3s^{2}\), y la configuración electrónica de un átomo de aluminio neutro con un electrón excitado se puede escribir como\(1s^{2}2s^{2}2p^{6}3s^{2}4s^{1}\).

Los electrones están etiquetados por cuatro números cuánticos: el número cuántico principal, el número cuántico acimutal, el número cuántico magnético y el número cuántico de espín [6] [12]. No hay dos electrones alrededor de un átomo que puedan tener el mismo conjunto de números cuánticos. El número cuántico principal toma valores enteros, 1, 2, 3 y así sucesivamente. Se dice que todos los electrones con el mismo número cuántico de principio están en la misma cáscara. Los grandes números en la configuración electrónica se refieren a los números cuánticos principales. El átomo de aluminio neutro en el estado de energía más baja tiene dos electrones en el caparazón 1, ocho electrones en el caparazón 2 y tres electrones en el caparazón 3. Para la mayoría de los átomos, especialmente los átomos con pocos electrones, los electrones con números cuánticos de principio más bajo están ambos espacialmente más cerca del núcleo y requieren la mayor cantidad de energía para eliminarlos. Sin embargo, hay excepciones a esta idea para algunos electrones alrededor de átomos más grandes [13] [14].

Los números cuánticos azimutales son enteros, y estos valores definen subshells. Para conchas con número cuántico principal\(\mathfrak{n}\), el número cuántico azimutal puede tomar valores de 0 a\(\mathfrak{n}-1\). En la configuración electrónica, los valores de este número cuántico se denotan con letras minúsculas:\(s =0\),\(p =1\),\(d =2\),\(f =3\), y así sucesivamente. Los números cuánticos magnéticos también son enteros, y estos valores definen orbitales. Para una subcapa con número cuántico azimutal\(l\), el número cuántico magnético toma valores de\(-l\) a\(l\). En la configuración electrónica, los números de superíndice indican el número cuántico magnético. Los números cuánticos de espín de electrones pueden tomar los valores\(\frac{1}{2}\) y\(\frac{-1}{2}\). No se denotan explícitamente en la configuración electrónica.

Consideremos nuevamente el átomo de aluminio neutro en el estado energético más bajo. Este átomo tiene electrones con números cuánticos principales\(\mathfrak{n}\) = 1, 2 y 3. Para los electrones con número cuántico principal 1, los únicos valores posibles tanto para el número cuántico acimutal como para el número cuántico magnético son cero. El número cuántico de giro puede tomar los valores de\(\frac{1}{2}\) y\(\frac{-1}{2}\). Solo dos electrones pueden ocupar el caparazón 1, y estos electrones se denotan por el\(1s^{2}\) término de la configuración de electrones. Para los electrones con principio número cuántico 2, el número cuántico azimutal puede ser 0 o 1. Dos electrones pueden ocupar el\(2s\) orbital, y seis electrones pueden ocupar el\(2p\) orbital. Para el shell 3, el número cuántico azimutal puede tomar tres valores posibles:\(s =0\),\(p =1\), y\(d =2\). Sin embargo, dado que el aluminio solo tiene 13 electrones, los electrones no tienen todos estos valores posibles, por lo que la capa 3 solo está parcialmente llena. Los átomos en la columna más a la derecha de la tabla periódica tienen conchas completamente llenas. Rara vez están involucrados en reacciones químicas porque agregar electrones, eliminar electrones o formar enlaces químicos requeriría demasiada energía.

Los electrones de valencia son los electrones que más fácilmente se arrancan de un átomo. Los electrones de valencia son los electrones involucrados en las reacciones químicas, y la corriente eléctrica es el flujo de electrones de valencia. Otros electrones, de capa interna, pueden estar involucrados en reacciones químicas o corriente eléctrica solo en casos de energías aplicadas inusualmente grandes, y estas situaciones no serán discutidas en este texto. Los electrones de valencia ocupan la subcapa o subcáscaras con los números cuánticos más altos, y los electrones de valencia no forman parte de conchas completamente llenas. Para el ejemplo del átomo de aluminio neutro en el estado de energía más baja, los tres electrones en la capa 3 son electrones de valencia.

¿Dónde están los electrones alrededor del átomo espacialmente? Esta pregunta es de interés para químicos, físicos e ingenieros eléctricos. Si conocemos el orbital de un electrón, tenemos alguna información sobre dónde es probable que el electrón se encuentre espacialmente alrededor de un átomo. Sin embargo, identificar la ubicación de un electrón con cualquier grado de precisión es difícil por múltiples razones. Primero, los átomos son diminutos, aproximadamente\(10^{-10}\) m de diámetro. Segundo, a cualquier temperatura por encima del cero absoluto, los átomos y electrones están continuamente en movimiento. Tercero, los electrones tienen propiedades similares a partículas y ondas. Cuarto, según el Principio de Incertidumbre de Heisenberg, la posición y el impulso de un electrón no pueden conocerse simultáneamente con total precisión. En el mejor de los casos, se puede decir que lo más probable es que un electrón esté en alguna región y se mueva con algún rango de velocidad. Quinto, en muchos materiales incluyendo conductores y semiconductores, los electrones de valencia son compartidos por muchos átomos en lugar de unirse a un átomo individual [10, p. 544].