2.2: Capacitores

Polarización de materiales

Cuando se aplica un voltaje externo a través de un aislante, las cargas se separan por todo el material, y esta separación de carga se denomina polarización del material. La polarización del material se puede definir con mayor precisión en términos de la intensidad del campo eléctrico\(\overrightarrow{E}\) y la densidad de flujo de desplazamiento\(\overrightarrow{D}\), dos campos vectoriales que aparecen en las ecuaciones de Maxwell, Ecuaciones 1.6.3 - 1.6.6. Estos campos vectoriales están relacionados por\[\overrightarrow{D} = \epsilon \overrightarrow{E}. \nonumber \]

¿Por qué definimos dos parámetros de campo eléctrico cuando solo son versiones escaladas entre sí? Es útil separar la descripción del campo eléctrico dentro de un material de la descripción del campo en el espacio libre. De manera similar, dos campos vectoriales describen el campo magnético, la intensidad del campo magnético\(\overrightarrow{H}\) y la densidad de flujo magnético\(\overrightarrow{B}\), y estos campos aparecen en las ecuaciones de Maxwell por la misma razón. La polarización del material\(\frac{C}{m^2}\),\(\overrightarrow{P}\) en unidades, se define como la diferencia entre el campo eléctrico en el material\(\overrightarrow{D}\) y el campo eléctrico que estaría presente en el espacio libre\(\overrightarrow{E}\). Más específicamente\[\overrightarrow{P} =\overrightarrow{D}-\epsilon_0 \overrightarrow{E} \nonumber \] o\[\overrightarrow{P} =(\epsilon - \epsilon_0) \overrightarrow{E}. \nonumber \]

Estas expresiones involucran la permitividad del espacio libre\(\epsilon_0\) y la permitividad de un material\(\epsilon\) que se definieron en Ondas Electromagnéticas y Materiales.

Los científicos sobrecargan tanto las palabras capacitancia como polarización con múltiples significados. Consulte el Apéndice C para obtener más detalles sobre los diferentes usos de estos términos.

Almacenamiento de Energía en Capacitores

Cuando se carga un condensador, la energía se convierte de energía eléctrica a energía almacenada en una polarización de material que es energía de la separación de carga. Cuando se descarga, la energía se convierte de la energía almacenada en la polarización del material de nuevo a la energía eléctrica de los electrones que fluyen. Los capacitores están hechos de un material aislante entre las placas conductoras. A medida que suministramos un voltaje a través del aislador, las cargas se acumulan en las placas. El voltaje acumulado es proporcional a la carga acumulada en las placas. \[Q =Cv \label{2.2.4} \]

En la Ecuación\ ref {2.2.4},\(Q\) está la carga en culombios,\(v\) es el voltaje, y la constante de proporcionalidad es la capacitancia\(C\) en faradios. Si tomamos la derivada con respecto al tiempo, obtenemos la expresión más familiar que relaciona la corriente y el voltaje a través del condensador. \[\frac{dQ}{dt} =i =C\frac{dv}{dt} \nonumber \]

La capacitancia de un condensador está relacionada con la permitividad del material dieléctrico entre los conductores. La permitividad es una medida de la cantidad de energía que puede ser almacenada por un material dieléctrico. Como se describe en la Ecuación 1.6.20, para un condensador de placa paralela esta relación es\[C =\frac{\epsilon A}{d_{thick}} \label{2.2.6} \]

donde\(A\) está el área de las placas y\(d_{thick}\) es la distancia entre las placas. La energía\(E\) almacenada en un condensador en función del voltaje aplicado a través de él viene dada por\[E =\frac{1}{2}Cv^2 =\frac{1}{2}Qv. \nonumber \]

La capacitancia de un condensador de placa paralela llena de vacío se describe mediante la Ecuación\ ref {2.2.6} con permitividad\(\epsilon = \epsilon_0\), la permitividad del espacio libre. A medida que cargamos el condensador, las cargas se acumulan en las placas, y no se produce ningún cambio en el vacío entre las placas. Si reemplazamos el vacío por un dieléctrico con\(\epsilon > \epsilon_0\), la capacitancia se hace más grande. El condensador lleno de dieléctrico puede almacenar más energía, todo lo demás igual, porque el material dieléctrico cambia a medida que se carga el condensador. Más específicamente, el material polariza. En un aislante, los electrones están unidos a sus átomos, y la corriente no puede fluir. En cambio, los electrones en un dieléctrico se mueven ligeramente con respecto a sus núcleos mientras siguen estando unidos a los átomos. Los electrones siempre están en movimiento para los materiales a temperaturas superiores al cero absoluto, pero cuando un material polariza, la ubicación neta de los electrones con respecto a los núcleos cambia. A medida que se carga el condensador, los electrones se desplazan ligeramente de sus átomos, equilibrando las cargas en las placas, y se almacena más energía en el dieléctrico para un voltaje dado. Decimos que este proceso induce dipolos eléctricos. Cuanto mayor es la permitividad\(\epsilon\), más el material puede almacenar energía polarizando de esta manera. Por esta razón, los capacitores suelen estar llenos de materiales dieléctricos como el dióxido de tántalo\(Ta_2O_5\) que tiene\(\epsilon = 25\epsilon_0\) [18]. Un material con\(\epsilon = 25\epsilon_0\), por ejemplo, podrá almacenar 25 veces la energía de un condensador lleno de aire del mismo tamaño con el mismo voltaje aplicado.

Permittividad y medidas relacionadas

Por razones históricas, la permitividad puede ser expresada por diferentes medidas. La susceptibilidad eléctrica\(\chi_e\), la permitividad relativa\(\epsilon_r\), el índice de refracción\(n\) y la permitividad\(\epsilon\) describen la capacidad de un material para almacenar energía en el campo eléctrico. La susceptibilidad eléctrica es una medida sin unidad relacionada con la permitividad por\[\chi_e = \frac{\epsilon}{\epsilon_0}-1 \nonumber \]

y la permitividad relativa es otra medida sin unidades definida por\[\epsilon_r = \frac{\epsilon}{\epsilon_0}. \nonumber \]

Con algo de álgebra, podemos escribir la polarización material en términos de la permitividad relativa o la susceptibilidad eléctrica. \[\overrightarrow{P} =(\epsilon_r-1)\epsilon_0\overrightarrow{E} =\epsilon_0\chi_e\overrightarrow{E} \nonumber \]

Los científicos que estudian la óptica suelen utilizar el índice de refracción, otra medida sin unidades que representa la relación entre la velocidad de la luz en el espacio libre y la velocidad de la luz en el material. \[n =\frac{c}{|\overrightarrow{v}|} = \frac{\text{speed of light in free space}}{\text{speed of light in material}} \nonumber \]

Dado que las ondas electromagnéticas no pueden viajar más rápido que la velocidad de la luz en el espacio libre, el índice de refracción de un material es mayor que uno,\(n > 1\). Suponiendo que un material es un buen aislante y\(\mu =\mu_0\), que suelen ser una suposición segura para la óptica, la relación entre el índice de refracción y la permitividad se simplifica a\[n =\sqrt{\epsilon_r}. \nonumber \]

La tabla\(\PageIndex{1}\) enumera las permitividades relativas de algunos aisladores utilizados para fabricar condensadores o dispositivos piezoeléctricos. Los valores son todos aproximados. Consulte las referencias citadas para obtener información más detallada.

En las definiciones de 1.6.3 y en Tabla\(\PageIndex{1}\), la permitividad se trata como una constante escalar, pero en algunos contextos se necesita una descripción más complicada. En un material cristalino, un voltaje aplicado a lo largo de un eje cristalográfico puede inducir la separación de carga en todo el material más fácilmente que un voltaje del mismo tamaño aplicado a lo largo de un eje diferente.

Cuadro\(\PageIndex{1}\): Valores aproximados de permitividad relativa de diversos materiales.

Material	Permittividad relativa\(\epsilon_r\)	Referencia
Vacío	\ (\ epsilon_r\) ">1.0	[3]
Teflón	\ (\ épsilon_r\) ">2.1	[3]
Polietileno	\ (\ épsilon_r\) ">2.3	[3]
Papel	\ (\ épsilon_r\) ">3.0	[3]
\(\text{SiO}_2\)	\ (\ épsilon_r\) ">3.5	[18]
Mica	\ (\ epsilon_r\) ">6.0	[3]
\(\text{Al}_2\text{O}_3\)	\ (\ épsilon_r\) ">9	[18]
\(\text{AlP}\)	\ (\ épsilon_r\) ">10.2	[9]
\(\text{ZrSiO}_4\)	\ (\ épsilon_r\) ">12.5	[19]
\(\text{Si}\)	\ (\ épsilon_r\) ">11.8	[9]
\(\text{Ge}\)	\ (\ épsilon_r\) ">16	[9]
\(\text{Ta}_2\text{O}_5\)	\ (\ épsilon_r\) ">24	[20]
\(\text{ZrO}_2\)	\ (\ épsilon_r\) ">25	[18]
\(\text{HfO}_2\)	\ (\ épsilon_r\) ">40	[18]
\(\text{TiO}_2\)	\ (\ épsilon_r\) ">50	[18]
\(\text{PbS}\)	\ (\ épsilon_r\) ">161	[9]
\(\text{PbSe}\)	\ (\ épsilon_r\) ">280	[9]
\(\text{BaSrTiO}_3\)	\ (\ épsilon_r\) ">300	[18]
\(\text{PbTe}\)	\ (\ épsilon_r\) ">360	[9]

Figura\(\PageIndex{1}\): Ilustración de polarización material.

En tales casos, el material se llama anisotrópico. La permitividad de los materiales anisotrópicos se describe con mayor precisión mediante una matriz.

\[ \begin{pmatrix} \epsilon_{xx} & \epsilon_{xy} & \epsilon_{xz} \\ \epsilon_{yx} & \epsilon_{yy} & \epsilon_{yz} \\ \epsilon_{zx} & \epsilon_{zy} & \epsilon_{zz} \end{pmatrix} \nonumber \]

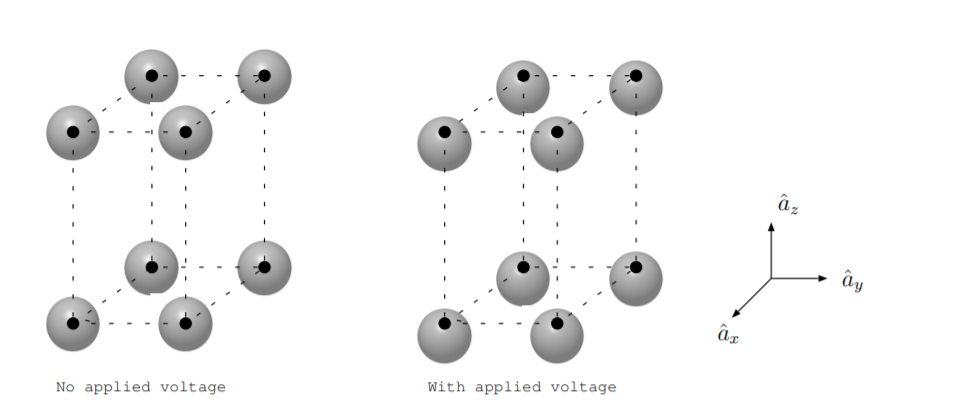
La parte izquierda de la Figura\(\PageIndex{1}\) muestra algunos átomos de un cristal. Los pequeños círculos negros representan la ubicación de los núcleos de átomos en los cristales, y los círculos grises representan la nube de electrones que rodea los núcleos de cada átomo. Si se aplica un campo eléctrico en la\(\hat{a}_z\) dirección, el material se polariza, por lo que los electrones se desplazan ligeramente con respecto a los núcleos como se muestra en la figura de la derecha. Dado que el espaciamiento de los átomos es diferente en la\(\hat{a}_y\) dirección\(\hat{a}_x\) y que en la\(\hat{a}_z\) dirección, el campo externo requerido para obtener el mismo desplazamiento de carga será diferente en las\(\hat{a}_y\) direcciones\(\hat{a}_x\) y que la\(\hat{a}_z\) dirección para este material. Por esta razón, el material ilustrado en la figura es anisotrópico, y la permitividad se describe mejor por una matriz en lugar de una cantidad escalar.

Propiedades del Capacitor

Los capacitores son dispositivos de conversión de energía utilizados en aplicaciones desde la estabilización de fuentes de alimentación hasta el filtrado de señales de comunicación y la separación de un desplazamiento de CC de una señal de CA. Aunque tanto los condensadores como las baterías almacenan energía eléctrica, la energía de las baterías se almacena en los enlaces químicos de los átomos de los electrodos mientras que la energía se almacena en los condensadores en la polarización del material de las cargas ligadas que se desplazan en una capa dieléctrica.

Figura\(\PageIndex{2}\): Rango de capacitancia y valores de voltaje máximo para varios tipos de condensadores, siguiendo [21] y [22].

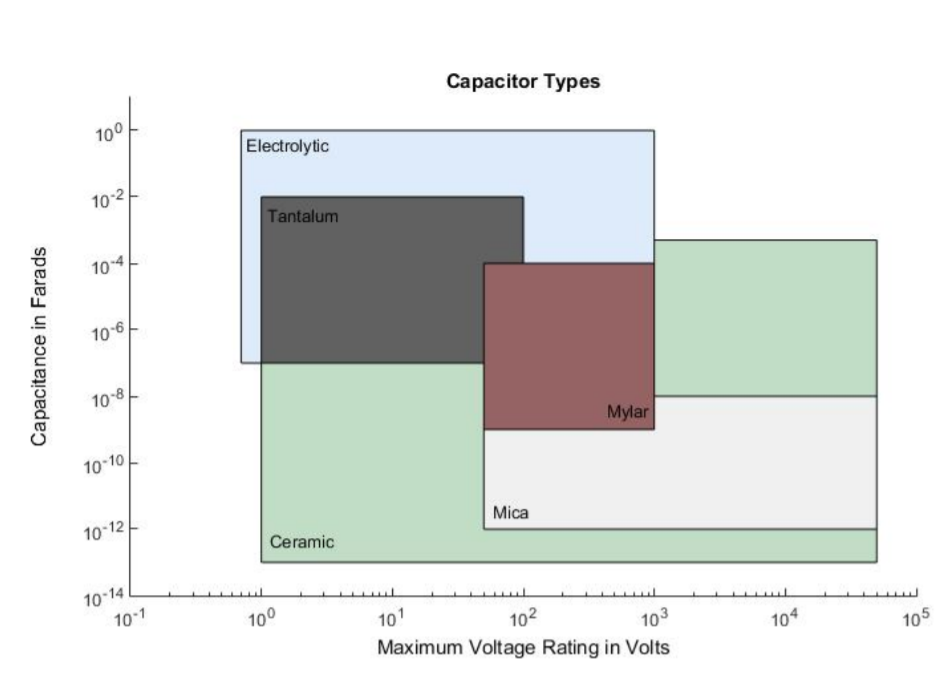
Las dos primeras medidas a considerar al seleccionar un condensador para usar en un circuito son la capacitancia y el voltaje máximo. Un condensador puede dañarse si se coloca en un circuito donde el voltaje a través de él excede el valor nominal máximo. Los rangos aproximados para estos parámetros para capacitores con diferentes materiales dieléctricos se muestran en la Figura\(\PageIndex{2}\). Los rangos de capacitancia están en el eje vertical y los rangos de voltaje máximo están en el eje horizontal. Por ejemplo, los condensadores electrolíticos a menudo se pueden encontrar con valores de capacitancia que van desde\(10^{-7}\) hasta 1 F y clasificaciones de voltaje máximo en el rango de 1 a 1000 V. De manera similar, los condensadores cerámicos a menudo se pueden encontrar con valores de capacitancia que van desde\(10^{-13}\) a\(5 \cdot 10^{-4}\) F y clasificaciones de voltaje máximo en el rango de 1 a 50,000 V.

Si bien la capacitancia y la clasificación de voltaje máximo son parámetros importantes a considerar, no son las únicas consideraciones. Otro factor a considerar es la estabilidad de la temperatura. Idealmente, la capacitancia será independiente de la temperatura. Sin embargo, todos los materiales tienen un coeficiente de temperatura distinto de cero. Los capacitores cerámicos y electrolíticos tienden a ser más sensibles a la variación de temperatura que los condensadores de polímero o vacío [22]. La precisión, o precisión, también es importante. Así como las resistencias están etiquetadas con tolerancias, los capacitores pueden tener tolerancias de, por ejemplo,\(\pm5\%\) o\(\pm10\%\). Otro factor a considerar es la resistencia en serie equivalente [23, ch. 1]. Todos los materiales tienen cierta resistividad, por lo que todos los capacitores tienen alguna resistencia finita. Para tener en cuenta la resistencia interna, podemos modelar cualquier condensador físico como un condensador ideal en serie con una resistencia ideal, y el valor de la resistencia utilizada se llama resistencia en serie equivalente. Además, se debe considerar la fuga de un condensador [22]. Si un condensador es capaz de retener su carga almacenada durante un largo período de tiempo, el condensador tiene pequeñas fugas. Si el condensador se descarga rápidamente incluso cuando se desconecta de un circuito, tiene grandes fugas. Un condensador ideal no tiene fugas [22]. Los capacitores también se diferencian por su vida útil. Un condensador ideal opera durante décadas sin degradación. Sin embargo, algunos tipos de capacitores, como los condensadores electrolíticos, no están diseñados para tener una larga vida útil [22]. Otros factores a considerar incluyen costo, disponibilidad, tamaño y respuesta de frecuencia [22].

Figura\(\PageIndex{3}\): Mica natural.

Como dieléctrico se utilizan cerámicas, vidrios, polímeros y otros materiales [22]. A menudo, los capacitores se clasifican por el material dieléctrico que contienen [22]. Los capacitores cerámicos son pequeños, baratos y fácilmente disponibles [22]. A menudo pueden tolerar grandes voltajes aplicados [22]. Por lo general, tienen valores de capacitancia pequeños, poca precisión, baja estabilidad de temperatura y fuga moderada [22]. Tienen baja resistencia en serie equivalente y pueden soportar mucha corriente, pero pueden causar picos de voltaje transitorios, [23, ch. 1]. Algunos capacitores cerámicos son piezoeléctricos. Si estos condensadores son vibrados, o incluso golpeados con un lápiz, se introducirá ruido en el circuito debido a la piezoelectricidad [23, ch. 12].

La mica es un material interesante que se utiliza como dieléctrico en capacitores. La figura\(\PageIndex{3}\) muestra mica natural recolectada en la mina Ruggles cerca de Grafton, New Hampshire. La mica viene en diferentes formas naturales incluyendo biotita y moscovita\(\text{KAl}_2(\text{AlSi}_3\text{O}_{10})(\text{OH})_2\) [24]. La mica es un mineral escamoso con una estructura en capas [24], por lo que los capacitores de mica se pueden hacer con capas dieléctricas muy delgadas. Los capacitores de mica a menudo tienen buena precisión y pequeñas fugas [22].

Figura\(\PageIndex{4}\): Capacitores de tamaño de orificio pasante.

Los dieléctricos de condensadores se han hecho de muchos tipos de polímeros, incluidos poliestireno, policarbonato, poliéster, polipropileno, teflón y mylar [22]. Estos capacitores a menudo tienen buena precisión, estabilidad de temperatura y características de fuga [22].

No todos los capacitores tienen dieléctricos sólidos. Un vacío es un dieléctrico. Los capacitores con dieléctrico de vacío se utilizan en aplicaciones que involucran alto voltaje o que requieren fugas muy bajas [22]. Capacitores con dieléctricos líquidos hechos de aceite se utilizan en situaciones similares [22]. Los capacitores electrolíticos a menudo tienen dieléctricos que son una combinación de materiales sólidos con electrolitos líquidos. Un electrolito es un líquido a través del cual algunas cargas pueden fluir más fácilmente que otras. Los capacitores electrolíticos están polarizados, es decir, que tienen terminales positivos y negativos, por lo que, similar a un diodo, la orientación del condensador en un circuito es importante. Dentro de un condensador electrolítico hay una unión de múltiples materiales. La aplicación inicial de voltaje en la fábrica crea químicamente una capa de óxido que es el dieléctrico. Invertir el voltaje disolverá el dieléctrico y destruirá el condensador. Una ventaja de los condensadores electrolíticos es que un dispositivo pequeño puede tener una gran capacitancia. Sin embargo, a menudo tienen poca precisión, estabilidad de temperatura y fugas [22]. Además, los condensadores electrolíticos tienen una vida útil finita porque el líquido puede degradarse con el tiempo.