2.3: Dispositivos piezoeléctricos

¿Podemos inducir una polarización material en un aislante de una manera que no implique aplicar voltaje? Si es así, entonces este método puede cargar un condensador, y podemos descargar el condensador como de costumbre para producir electricidad. Cualquier dispositivo que realice esta tarea es un dispositivo de conversión de energía. Los dispositivos piezoeléctricos, piroeléctricos y electroópticos implican este tipo de conversión de energía, y actualmente todos están disponibles como sensores y como otros productos. En los dispositivos piezoeléctricos, discutidos en esta sección, una tensión mecánica provoca una polarización del material.

Si se ejerce una tensión lo suficientemente grande sobre un material, la estructura cristalina cambiará. Por ejemplo, a temperatura y presión suficientemente altas, el carbón cristalizará en diamante, y cuando se elimina la presión, el material permanece en forma de diamante. El acero se puede endurecer golpeándolo repetidamente en un proceso llamado granallado. Se necesita una cantidad significativa de energía para cambiar permanentemente la estructura cristalina de un material. En esta sección, no estamos discutiendo este efecto. En cambio, estamos discutiendo un efecto que normalmente requiere poca energía. Cuando se ejerce una tensión mecánica sobre un dispositivo piezoeléctrico, se establece una polarización de material. Los electrones de valencia son desplazados, pero los núcleos del material y otros electrones no se mueven. Cuando liberamos el estrés, la polarización material desaparece.

Constante de tensión piezoeléctrica

Podemos describir la polarización material de un material aislante piezoeléctrico incorporando un término que depende de la tensión mecánica aplicada, [25].

\[\overrightarrow{P} =\overrightarrow{D} - \epsilon_0\overrightarrow{E} +d\overrightarrow{\varsigma} \label{2.3.1} \]

En esta ecuación\(\overrightarrow{P}\) se encuentra la polarización del material en\(\frac{C}{m^2}\),\(\overrightarrow{D}\) es densidad de flujo de desplazamiento en\(\frac{C}{m^2}\),\(\epsilon_0\) es la permitividad del espacio libre en\(\frac{F}{m}\),\(\overrightarrow{E}\) es la intensidad del campo eléctrico aplicado en\(\frac{V}{m}\),\(d\) es la constante de tensión piezoeléctrica en \(\frac{m}{V}\), y\(\overrightarrow{\varsigma}\) es el estrés en los pascales. El estrés también se puede dar en otras unidades.

\[1 Pa =1 \frac{J}{m^3} = 1 \frac{N}{m^2} \nonumber \]

Para muchos materiales, la constante de deformación piezoeléctrica\(d\) es cero, y para muchos otros materiales,\(d\) es bastante pequeña. El titanato de bario se utiliza para fabricar sensores piezoeléctricos porque tiene un coeficiente de deformación piezoeléctrico relativamente grande,\(d \approx 3 \cdot 10^{-10} \frac{m}{V}\) [25, p. 408]. Coeficientes de ejemplo adicionales se dan en el siguiente capítulo en la Tabla 3.1.1.

La deformación mecánica es una medida sin unidad de deflexión o deformación mientras que la tensión tiene unidades pascales. Sin un campo eléctrico externo, estas cantidades están relacionadas por el módulo elástico de Young que tiene unidades\(\frac{N}{m^2}\). \[ \text{strain} =( \frac{1}{\text{Young's elastic modulus}}) \cdot \text{stress} \nonumber \]

Si también se aplica un campo eléctrico, la tensión y la deformación están relacionadas por\[ \text{strain} =( \frac{1}{\text{Young's elastic modulus}} ) \cdot \text{stress} + \overrightarrow{E} \cdot d \nonumber \]

donde\(d\) es la constante de deformación piezoeléctrica. La energía almacenada en un dispositivo piezoeléctrico bajo tensión\(\overrightarrow{\varsigma}\) viene dada por\[E = |\overrightarrow{\varsigma}| \cdot A \cdot l \cdot \eta_{eff} \nonumber \]

donde\(A\) es el área de la sección transversal de un dispositivo en\(m^2\),\(l\) es la deformación en m, y\(\eta_{eff}\) es la eficiencia. Los dispositivos que son más grandes, se deforman más o están hechos de materiales con constantes piezoeléctricas más grandes almacenan más energía.

Según la Ecuación\ ref {2.3.1}, la polarización material de un cristal aislante es linealmente proporcional a la tensión aplicada. Si bien esto describe con precisión muchos materiales, es una mala descripción de otros materiales. Para otros cristales piezoeléctricos, la polarización del material es proporcional al cuadrado de la tensión aplicada\[ |\overrightarrow{P}| = |\overrightarrow{D}| - \epsilon_0 |\overrightarrow{E}| + d |\overrightarrow{\varsigma}| + d_{quad} {|\overrightarrow{\varsigma}|}^2 \label{2.3.6} \]

donde\(d_{quad}\) hay otra constante de deformación piezoeléctrica. Para modelar la polarización material en otros materiales, se necesitan términos que involucren mayores potencias de la tensión.

Piezoelectricidad en Materiales Cristalinos

Para entender qué materiales son piezoeléctricos, necesitamos introducir alguna terminología para describir los cristales. Los materiales cristalinos pueden estar compuestos de elementos, tales como\(\text{Si}\), o compuestos, tales como\(\text{NaCl}\). Por definición, los átomos en los cristales se disponen periódicamente. Se especifican dos componentes para describir la disposición de los átomos en un cristal: una celosía y una base [25, p. 4]. Una celosía es una matriz periódica de puntos en el espacio. Una red\(\mathfrak{n}\) -dimensional se especifica por vectores de\(\mathfrak{n}\) celosía para entero\(\mathfrak{n}\). Podemos llegar de un punto de celosía a cada otro punto de celosía viajando un número entero de vectores de celosía. Tres vectores,\(\overrightarrow{a_1}\),\(\overrightarrow{a_2}\), y\(\overrightarrow{a_3}\) se utilizan para describir celosías físicas en tres espacios. La elección de los vectores de celosía no es única. Los vectores de celosía que son lo más cortos posible se denominan vectores de celosía primitivos. Una celda de una celosía es el área (2D) o volumen (3D) formada por vectores de celosía. Una celda primitiva es el área o volumen formado por vectores de celosía primitivos, y es la unidad repetitiva más pequeña posible la que describe una celosía.

Figura\(\PageIndex{1}\): Ilustración bidimensional de los términos celosía, base, estructura cristalina y vector de celosía primitiva.

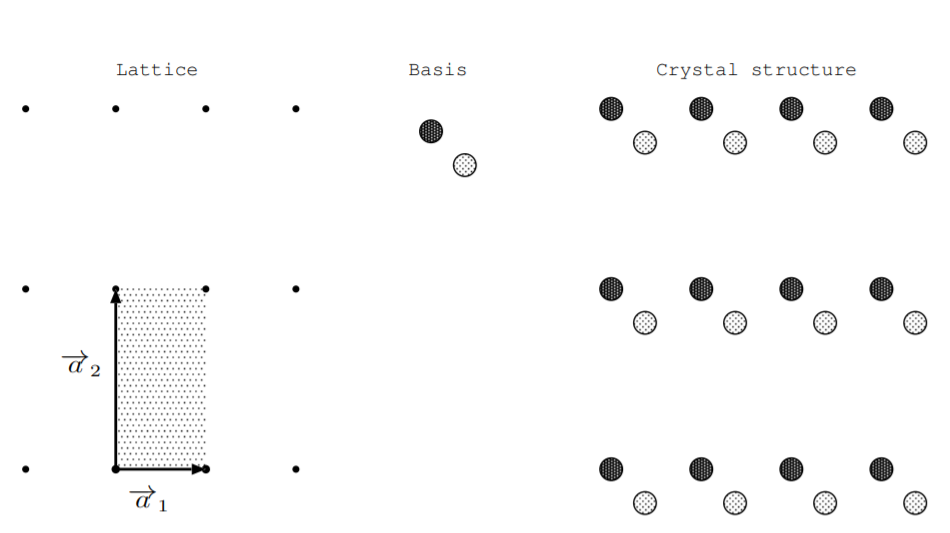
Para especificar la estructura de un material, adjuntamos uno o más átomos a cada punto de la celosía. Esta disposición de átomos se llama base cristalina. La base de celosía y cristal juntos definen la estructura cristalina [25]. La figura\(\PageIndex{1}\) muestra un ejemplo bidimensional de una celosía, base cristalina y estructura cristalina. Dado que este ejemplo es bidimensional, solo se necesitan dos vectores de celosía para especificar la celosía. Se muestran dos vectores de celosía primitivos y se sombrea una celda primitiva.

Hay 14 posibles tipos de celosías tridimensionales, y estos se llaman celosías Bravais [25]. Cada una de estas posibles celosías tiene un nombre descriptivo. La figura\(\PageIndex{2}\) muestra cuatro de las posibles celosías Bravais: cúbico simple, cúbico centrado en el cuerpo, cúbico centrado en la cara y triclínico asimétrico. En la celosía cúbica simple, todos los ángulos entre los segmentos de línea que conectan los puntos vecinos más cercanos son ángulos rectos, y todas las longitudes entre los puntos vecinos más cercanos son iguales. En la red triclínica asimétrica, ninguno de estos ángulos son ángulos rectos, y ninguna de estas longitudes entre los puntos vecinos más cercanos es igual. La figura\(\PageIndex{2}\) muestra celdas de celosía, pero las celdas para las celosías cúbicas centradas en el cuerpo y cúbicas centradas en la cara no son celdas primitivas porque se pueden encontrar unidades repetitivas

Consideremos algunos ejemplos de celosías y estructuras cristalinas. La estructura cristalina del cloruro de sodio, por ejemplo, involucra una red cúbica centrada en la cara y una base compuesta por un átomo de sodio y un átomo de cloro. Otro ejemplo es el silicio que cristaliza en lo que se conoce como la estructura diamantada [25]. Esta estructura cristalina involucra una celosía cúbica centrada en la cara y una base compuesta por dos átomos de silicio, en la ubicación (0, 0, 0) y\((\frac{l}{4},\frac{l}{4},\frac{l}{4})\) donde\(l\) está la longitud de la celda primitiva. El carbono\(\text{Si}\),\(\text{Ge}\), y\(\text{Sn}\) todos cristalizan en esta estructura de diamante con longitudes de celda de\(l\) = 0.356, 0.543, 0.565 y 0.646 nm respectivamente [25].

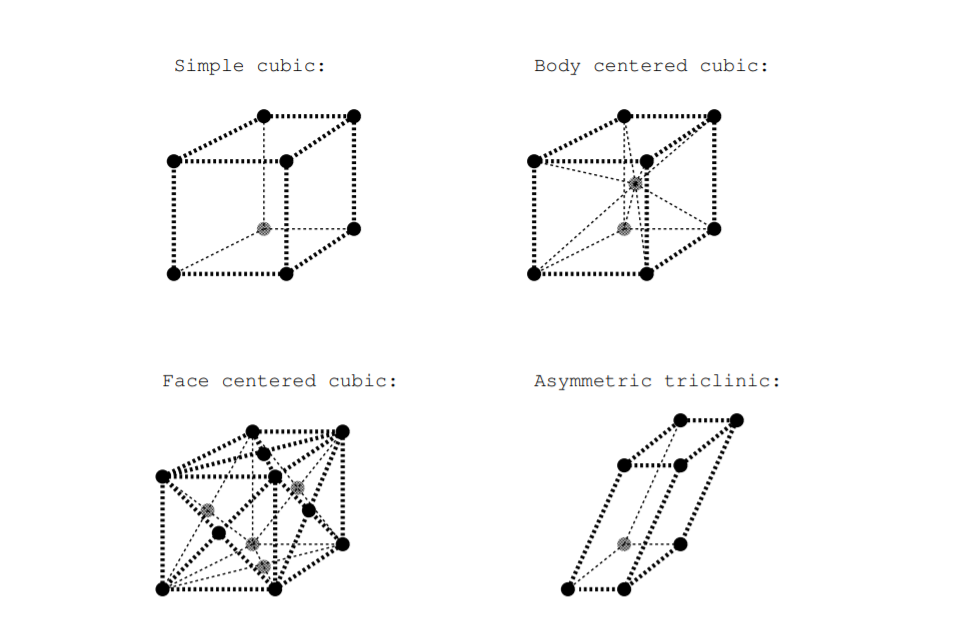
Figura\(\PageIndex{2}\): Ilustración de algunas celosías de Bravais.

Si bien solo hay 14 posibles celosías tridimensionales, hay significativamente más estructuras cristalinas posibles porque la estructura cristalina también incorpora la base. No es posible enumerar todas las estructuras cristalinas posibles. En cambio, se clasifican en función de las simetrías que contienen. Las posibles operaciones de simetría son rotaciones de 2, 3 veces, 4 y 6 veces, planos de espejo horizontales y verticales e inversión. Las estructuras cristalinas se agrupan en función de los elementos de simetría que contienen en clases llamadas grupos de puntos de cristal. Hay 32 posibles grupos de puntos cristalinos, y se enumeran en la Tabla\(\PageIndex{1}\).

Algunos autores clasifican las estructuras cristalinas en grupos de espacio cristalino en lugar de grupos de puntos cristalinos [6] [26]. Si bien hay 32 grupos de puntos de cristal, hay 230 grupos de espacios cristalinos. Los grupos de espacios cristalinos se basan en transformaciones de simetría que pueden incorporar no solo rotaciones y planos de espejo, sino también una combinación de traslaciones junto con rotaciones y planos de espejo. Los grupos de espacio cristalino no se discutirán más en este texto.

Cuadro\(\PageIndex{1}\): Resumen de grupos de puntos cristalinos.

Hermann- Notación Mauguin	Notación de Schoenflies	Sistema de Cristal	Ángulos de Celda Primitiva	Longitudes de Celda Primitiva	Piezoelec., Electro óptica Pockels, Simetría sin inversión	Piroeléctrico
1	\(C_1\)	triclínica	\( \alpha , \beta , \gamma \neq 90^{\circ} \)	\(a \neq b \neq c\)	y	y
\(\bar{1}\)	\(S_2\)	triclínica	\( \alpha , \beta , \gamma \neq 90^{\circ} \)	\(a \neq b \neq c\)	n	n
2	\(C_2\)	monoclínico	\( \alpha , \gamma = 90^{\circ}, \beta \neq 90^{\circ} \)	\(a \neq b \neq c\)	y	y
\(m\)	\(C_{1h}\)	monoclínico	\( \alpha , \gamma = 90^{\circ}, \beta \neq 90^{\circ} \)	\(a \neq b \neq c\)	y	y
\(\frac{2}{m}\)	\(C_{2h}\)	monoclínico	\( \alpha , \gamma = 90^{\circ}, \beta \neq 90^{\circ} \)	\(a \neq b \neq c\)	n	n
222	\(D_2, V\)	ortorrómbico	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a \neq b \neq c\)	y	n
2mm	\(C_{2v}\)	ortorrómbico	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a \neq b \neq c\)	y	y
\(\frac{2}{m}\frac{2}{m}\frac{2}{m}\)	\(D_{2h}, V_h\)	ortorrómbico	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a \neq b \neq c\)	n	n
4	\(C_4\)	tetragonal	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b \neq c\)	y	y
\(\bar{4}\)	\(S_4\)	tetragonal	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b \neq c\)	y	n
\(\frac{4}{m}\)	\(C_{4h}\)	tetragonal	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b \neq c\)	n	n
422	\(D_4\)	tetragonal	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b \neq c\)	y	n
\(4mm\)	\(C_{4v}\)	tetragonal	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b \neq c\)	y	y
\(\bar{4}2m\)	\(D_{2d}, V_d\)	tetragonal	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b \neq c\)	y	n
\(\frac{4}{m}\frac{2}{m}\frac{2}{m}\)	\(D_{4h}\)	tetragonal	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b \neq c\)	n	n
3	\(C_3\)	trigonal	\( \alpha , \beta , \gamma \neq 90^{\circ} \)	\(a = b = c\)	y	y
\(\bar{3}\)	\(S_6\)	trigonal	\( \alpha , \beta , \gamma \neq 90^{\circ} \)	\(a = b = c\)	n	n
32	\(D_3\)	trigonal	\( \alpha , \beta , \gamma \neq 90^{\circ} \)	\(a = b = c\)	y	n
\(3m\)	\(C_{3v}\)	trigonal	\( \alpha , \beta , \gamma \neq 90^{\circ} \)	\(a = b = c\)	y	y
\(\bar{3}\frac{2}{m}\)	\(D_{3d}\)	trigonal	\( \alpha , \beta , \gamma \neq 90^{\circ} \)	\(a = b = c\)	n	n
6	\(C_6\)	hexagonal	\( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \)	\(a = b \neq c\)	y	y
\(\bar{6}\)	\(C_{3h}\)	hexagonal	\( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \)	\(a = b \neq c\)	y	n
\(\frac{6}{m}\)	\(C_{6h}\)	hexagonal	\( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \)	\(a = b \neq c\)	n	n
622	\(D_6\)	hexagonal	\( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \)	\(a = b \neq c\)	y	n
\(6mm\)	\(C_{6v}\)	hexagonal	\( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \)	\(a = b \neq c\)	y	y
\(\bar{6}m2\)	\(D_{3h}\)	hexagonal	\( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \)	\(a = b \neq c\)	y	n
\(\frac{6}{m}\frac{2}{m}\frac{2}{m}\)	\(D_{6h}\)	hexagonal	\( \alpha = \beta = 90^{\circ}, \gamma = 120^{\circ} \)	\(a = b \neq c\)	n	n
23	\(T\)	cúbico (isométrico)	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b = c\)	y	n
\(\frac{2}{3}\bar{m}\)	\(T_h\)	cúbico (isométrico)	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b = c\)	n	n
432	\(O\)	cúbico (isométrico)	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b = c\)	y	n
\(\bar{4}3m\)	\(T_d\)	cúbico (isométrico)	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b = c\)	y	n
\(\frac{4}{m}\bar{3}\frac{2}{m}\)	\(O_h\)	cúbico (isométrico)	\( \alpha , \beta , \gamma = 90^{\circ} \)	\(a = b = c\)	n	n

Figura\(\PageIndex{3}\): Formas utilizadas para ilustrar elementos de simetría.

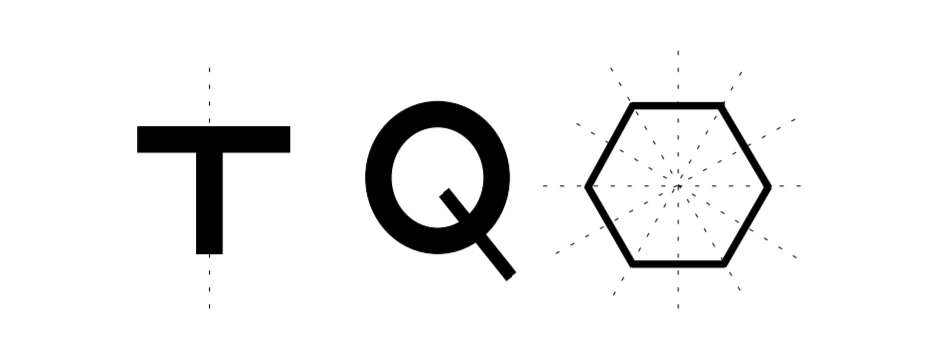
Como ejemplo de identificación de elementos de simetría, considere las formas 2D en la Figura\(\PageIndex{3}\). La figura en forma de T tiene un elemento de simetría, una simetría de plano espejo. La forma se ve igual si se refleja sobre el plano espejo que se muestra en la figura por una línea punteada. La forma Q no tiene elementos de simetría. El hexágono tiene múltiples elementos de simetría. Contiene rotación de 2 veces porque se ve igual cuando se gira por\(180^{\circ}\). También tiene simetrías de rotación de 3 y 6 veces porque se ve igual cuando se gira por\(60^{\circ}\) y\(30^{\circ}\) respectivamente. También tiene múltiples planos de espejo mostrados por líneas punteadas en la figura. En este ejemplo, se identifican elementos de simetría de formas 2D, pero los científicos de materiales están interesados en identificar simetrías de estructuras cristalinas 3D para obtener información sobre las propiedades de los materiales. Los materiales se clasifican en categorías llamadas grupos de puntos cristalinos en función de las simetrías de sus estructuras cristalinas.

Generalizamos sobre materiales cristalinos en base a si su estructura cristalina posee o no simetría de inversión. ¿Cuál es la operación de inversión? En 2D, la inversión es lo mismo que una rotación por\(180^{\circ}\). En 3D, una forma o estructura cristalina contiene simetría de inversión si es idéntica cuando se gira\(180^{\circ}\) e invierte a través del origen [24, p. 269]. Más específicamente, dibuja un vector\(\overrightarrow{V}\) desde el centro de la forma hasta cualquier punto de la superficie. Si la forma tiene simetría de inversión, entonces para cualquier vector de este tipo\(\overrightarrow{V}\), el punto a una\(\overrightarrow{V}\) distancia del origen también está en la superficie de la forma. El ejemplo a la izquierda de la Figura\(\PageIndex{4}\) tiene simetría de inversión porque para cualquier vector\(\overrightarrow{V}\) de este tipo desde el centro de la forma hasta un punto en la superficie, hay un punto en la superficie un vector\(\overrightarrow{V}\) alejado del origen también. El ejemplo de la derecha no contiene simetría de inversión como lo ilustra el vector\(\overrightarrow{V}\) mostrado por la flecha.

Figura\(\PageIndex{4}\): La forma de la izquierda contiene simetría de inversión mientras que la forma de la derecha no.

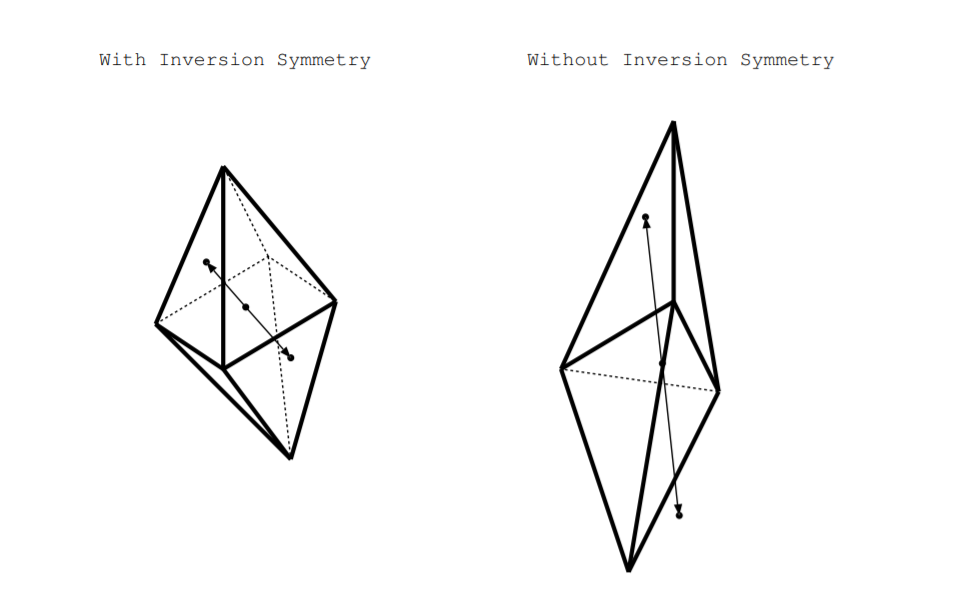
Si una estructura cristalina tiene simetría de inversión, decimos que el cristal tiene un centro de simetría de lo contrario decimos que es no centrosimétrico. Las estructuras cristalinas se clasifican en clases llamadas grupos de puntos cristalinos, y veintiuno de los 32 grupos de puntos no tienen centro de simetría por lo tanto no contienen simetría de inversión [24, p. 35]. Veinte de estos grupos de puntos cristalinos tienen un eje polar, algunos ejes en el cristal con diferentes formas en extremos opuestos del eje. Estos veintiún grupos de puntos cristalinos se especifican como no centrosimétricos en la sexta columna de la Tabla\(\PageIndex{1}\). Si presionamos mecánicamente estos materiales a lo largo del eje polar, se acumularán diferentes cantidades de cargas en los diferentes lados del eje. Los materiales cristalinos dieléctricos cuya estructura cristalina pertenece a cualquiera de estos 21 de estos grupos de puntos cristalinos no centrosimétricos son piezoeléctricos [24].

En la tabla se\(\PageIndex{1}\) enumeran todos los grupos de puntos cristalinos y se resume si los materiales cristalinos cuya estructura cristalina pertenece a cada grupo pueden ser piezoeléctricos, piroeléctricos y electroópticos Pockels. La piroelectricidad y la electro-óptica se discuten en el siguiente capítulo. La información en la tabla proviene de las referencias [24] [26] [27] [28]. Las dos columnas de la izquierda enumeran los 32 posibles grupos de puntos de cristal. Existen dos formas diferentes, pero equivalentes, de etiquetar los grupos de puntos cristalinos. La primera columna nombra los grupos de puntos de cristal usando la notación Hermann-Mauguin. Esta notación data de la década de 1930 y es utilizada por químicos, mineralogistas y algunos físicos. La segunda columna nombra los grupos de puntos de cristal usando la notación Schoenflies. La notación de Schoenflies data de 1891 [29], y es utilizada por matemáticos, espectroscopistas y otros físicos.

Figura\(\PageIndex{5}\): Etiquetas en una celda primitiva de una celosía

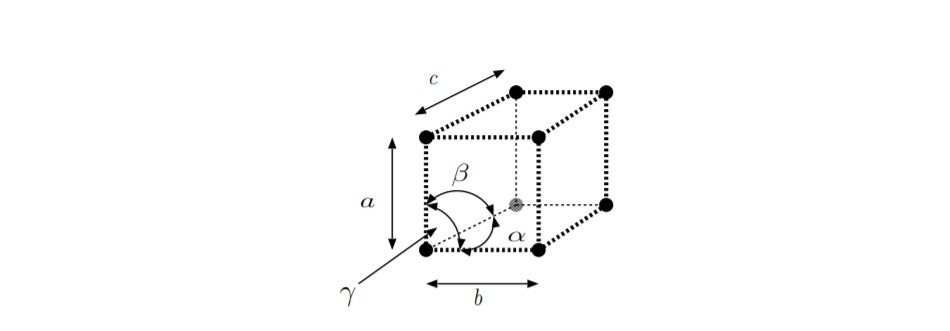
La tercera columna de Table\(\PageIndex{1}\) enumera el sistema de cristal. Como se muestra en la Figura\(\PageIndex{5}\):, los ángulos de una celda primitiva de una celosía están etiquetados\(\alpha,\)\(\beta,\) y\(\gamma\), y las longitudes de los lados están etiquetadas\(a,\)\(b,\) y\(c\). Los grupos de puntos cristalinos se pueden clasificar en función de los ángulos y longitudes de la celda primitiva de la red que pertenece a ese grupo. La literatura contiene múltiples formas sutilmente diferentes de definir los sistemas cristalinos [30]. La información de la tercera columna sigue a la referencia [28]. La cuarta columna da relaciones entre los ángulos de la celda primitiva. La quinta columna da relaciones entre las longitudes de los lados de la celda primitiva. Las combinaciones de ángulos y longitudes no son exclusivas de una fila específica. Por ejemplo, las clases\(C_2\) y\(C_{1h}\) ambas tienen\(\alpha = 90^{\circ} ,\)\(\beta \neq 90^{\circ} ,\)\(\gamma = 90^{\circ}\), y\(a \neq b \neq c\). Sin embargo, las estructuras cristalinas que pertenecen a estos grupos de puntos cristalinos contienen diferentes elementos de simetría. Para más detalles sobre específicamente qué elementos de simetría están contenidos en qué grupo de puntos cristalinos, véase [24] [26] [27] [28]. La sexta columna enumera si el grupo de puntos de cristal tiene simetría de inversión o no. Las estructuras cristalinas sin simetría de inversión o centro de simetría, llamadas no centrosimétricas, son tanto piezoeléctricas como electroópticas Pockels. La última columna enumera si los materiales cristalinos cuya estructura cristalina pertenece a los diversos grupos de puntos cristalinos pueden ser piroeléctricos o no.

Es posible comenzar con una estructura cristalina de un material, derivar los elementos de simetría que contiene, derivar si el material es piezoeléctrico o no, y derivar si el material es piroeléctrico o no. Además, es posible derivar a lo largo de qué ejes puede ocurrir piezoelectricidad o piroelectricidad en el material. Sin embargo, esta derivación está más allá del alcance de este libro. Para más detalles, véase [6] [27] [28] [31].

Para predecir si un material cristalino dieléctrico es piezoeléctrico o no, identifique su base reticular y cristalina para identificar su estructura cristalina. Identificar las simetrías de la estructura cristalina para clasificar su estructura cristalina en un grupo determinado de puntos cristalinos. Si esa estructura cristalina contiene simetría de inversión, el material puede ser piezoeléctrico. A menudo no tenemos que pasar por todos estos pasos porque el grupo de puntos cristalinos para muchos materiales cristalinos está tabulado [32]. Incluso si la estructura cristalina de un material contiene simetría de inversión, el efecto piezoeléctrico y el coeficiente de deformación piezoeléctrico\(d\) pueden ser demasiado pequeños para medirlos.

El efecto solo puede ocurrir cuando se tensiona el material a lo largo de algún eje en particular, y puede que no ocurra para una tensión mecánica de una orientación arbitraria con respecto a la dirección de los ejes del cristal. Solo hay un grupo de puntos cristalinos, llamado triclínico asimétrico, donde una tensión aleatoria producirá una polarización material [24]. Para todos los demás grupos de puntos, solo las tensiones a lo largo de ciertos ejes producirán una polarización material [24]. Además, en la mayoría de los cristales una cantidad dada de tensión a lo largo de un eje del cristal producirá una cantidad diferente de polarización del material que la misma cantidad de tensión aplicada a lo largo de un eje cristalográfico diferente. Cualitativamente, comprimir un cristal a lo largo de un eje puede causar más desplazamiento de carga que comprimir un cristal a lo largo de un eje diferente. Por esta razón, es más preciso tratar el coeficiente de deformación piezoeléctrica como una matriz. Esta matriz 3x6 tiene elementos\[d_{ik} =\left. \left(\frac{\partial\text{strain along k}}{\partial\text{electric field along i}}\right)\right|_{\text{for a given stress}} \nonumber \]

donde el campo eléctrico tiene\(x,\)\(y,\) y\(z\) componentes, y la tensión se puede aplicar a lo largo de las\(zz\) direcciones\(xx,\)\(xy,\)\(xz,\)\(yy,\)\(yz,\) o.

Piezoelectricidad en Materiales Amorfos y Policristalinos y Ferroelectricidad

En la sección anterior se discutió la piezoelectricidad en cristales. Podemos discutir simetrías de la estructura cristalina de los materiales cristalinos, pero ni siquiera podemos definir una estructura cristalina para materiales amorfos. Sin embargo, es posible fabricar dispositivos piezoeléctricos a partir de materiales policristalinos y amorfos. En un dieléctrico, si aplicamos un campo eléctrico externo, se induce una polarización material. Los dipolos eléctricos se forman porque los electrones y núcleos de los átomos se desplazan ligeramente entre sí. La ley de Coulomb nos dice que las acumulaciones de carga, como estos dipolos eléctricos, inducen un campo eléctrico. Entonces, si aplicamos un campo eléctrico externo a un dieléctrico, este efecto primario induce una polarización material, y esta polarización material, como efecto secundario, inducirá polarización adicional del material en el material. Una vez que un átomo se polariza formando un dipolo eléctrico, los átomos cercanos se polarizarán. Las regiones pequeñas del mismo material de polarización se denominan dominios eléctricos.

En ciertos materiales dieléctricos, una tensión mecánica externa induce una polarización local del material. La acumulación de carga de esta polarización material induce una polarización material en átomos cercanos formando dominios eléctricos [23]. Este efecto piezoeléctrico puede ocurrir tanto si el material original es cristalino, amorfo o policristalino [23]. En los materiales no cristalinos, este efecto es necesariamente no lineal, por lo que estos materiales no están bien descritos por las Ecuaciones\ ref {2.3.1} o\ ref {2.3.6}.

El proceso no lineal de una polarización material de un átomo que induce una polarización material de átomos cercanos causando la formación de dominios eléctricos se llama ferroelectricidad. Los materiales ferroeléctricos pueden ser cristalinos, amorfos o policristalinos. Veremos en el próximo capítulo que los materiales pueden ser piroeléctricos ferroeléctricos y ferroeléctricos electroópticos además de ferroeléctricos piezoeléctricos. El efecto ferroeléctrico está limitado por la temperatura. Para muchos materiales ferroeléctricos, estos efectos ocurren solo por debajo de alguna temperatura, llamada temperatura de Curie. Cuando los materiales se calientan por encima de la temperatura de Curie, el efecto ferroeléctrico desaparece [33]. La polarización material de un material ferroeléctrico puede depender de si previamente se ha inducido o no una polarización de material. Si el estado de un material depende de su historia pasada, decimos que el material tiene histéresis. Los materiales ferroeléctricos pueden tener una polarización de material incluso en ausencia de una tensión mecánica externa o campo eléctrico si previamente se ha aplicado una fuente de energía.

Mientras que el prefijo ferro- significa hierro, la mayoría de los materiales ferroeléctricos no contienen hierro, y la mayoría de los materiales que contienen hierro no son ferroeléctricos. La palabra ferroeléctrico se utiliza como analogía a la palabra ferromagnético. Algunos materiales que contienen hierro son ferromagnéticos. Si se aplica un campo magnético externo a través de un material ferromagnético, se establece un campo magnético interno en el material. Los materiales ferromagnéticos pueden tener un dipolo magnético permanente incluso en ausencia de un campo magnético aplicado. Podemos modelar un dipolo eléctrico como un par de cargas. Podemos modelar un dipolo magnético como un pequeño bucle de corriente. Los materiales ferromagnéticos presentan histéresis, y tienen dominios magnéticos donde los dipolos magnéticos están alineados.

Originalmente, un material ferroeléctrico piezoeléctrico tiene dominios eléctricos alineados aleatoriamente y sin polarización neta de material, por lo que comienza como ni piezoeléctrico ni ferroeléctrico. El proceso de hacer que un material exhiba piezoelectricidad y ferroelectricidad se llama polarización. Para polear un material, colóquelo en un campo eléctrico externo fuerte [23], por ejemplo, a través de los polos de una batería, de ahí el término. La polarización no cambia la estructura atómica, por lo que si el material fue originalmente amorfo, permanecerá amorfo. Durante este proceso, se forman dominios eléctricos, y estos dominios permanecen incluso cuando se elimina el campo externo. Un material que es piezoeléctrico debido a este tipo de polarización a veces se llama electreto [15, p. 297]. Después de que el material es polarizado, puede tener una polarización neta del material en todas partes. Además, después de la polarización, es piezoeléctrico y ferroeléctrico, por lo que una tensión mecánica externa induce una polarización del material localmente y en todo el material.

Materiales utilizados para fabricar dispositivos piezoeléctricos

¿Qué hace que un material sea bueno para un sensor piezoeléctrico o un dispositivo de conversión de energía piezoeléctrica? Los primeros dispositivos piezoeléctricos están hechos de aisladores eléctricos. Cuando se aplica un voltaje externo a través de un conductor, los electrones de valencia se eliminan de sus átomos, por lo que no se acumula polarización de material. En segundo lugar, los dispositivos piezoeléctricos están hechos de materiales con grandes constantes de tensión piezoeléctricas. La constante de deformación piezoeléctrica es tan pequeña que no se puede detectar en muchos cristales con estructuras cristalinas de uno de los 21 grupos de puntos cristalinos conocidos por ser piezoeléctricos, y es cero en cristales de los otros grupos de puntos cristalinos. En tercer lugar, los dispositivos piezoeléctricos deben estar hechos de materiales que no sean quebradizos para que puedan soportar tensiones repetidas sin daños permanentes. Las propiedades térmicas también pueden ser importantes [33]. No hay material que sea mejor en todas las aplicaciones.

El cuarzo, cristalino\(\text{SiO}_2\), fue el primer material en el que se estudió la piezoelectricidad. Pierre y Jacques Curie descubrieron el efecto en el cuarzo en la década de 1880 [3]. Hoy en día, muchos dispositivos piezoeléctricos, incluidos los osciladores de cristal, están hechos de cuarzo. El titanato de plomo y circonio es otro material utilizado debido a su constante de deformación piezoeléctrica relativamente alta [3] [34]. En aplicaciones que requieren flexibilidad y la capacidad de soportar tensiones mecánicas repetidas sin daños, se utilizan polímeros como el fluoruro de polivinilo [25]. También se ha estudiado la piezoelectricidad en materiales que incluyen titanato de bario\(\text{BaTiO}_3\), niobato de litio, turmalina

\[\text{(Na,Ca)(Li,Mg,Al)}_3 \text{(Al,Fe,Mn)}_6 ( \text{BO}_3)_3 (\text{Si}_6\text{O}_8)\text{(OH)}_4 , \nonumber \]

y sal Rochelle

\[\text{KNaC}_4\text{H}_4\text{O}_6 \cdot 4\text{H}_2\text{O} \nonumber \]

[3] [23] [24] [34].

Los fabricantes de dispositivos piezoeléctricos no suelen etiquetar sus productos para decir si están hechos de materiales cristalinos, amorfos o policristalinos, pero existen ventajas y desventajas en los diferentes tipos de materiales. Una ventaja de fabricar dispositivos piezoeléctricos a partir de materiales policristalinos o amorfos es que los dispositivos pueden fabricarse más fácilmente en diferentes formas como cilindros y esferas [33]. Sin embargo, los materiales utilizados a menudo tienen temperaturas de fusión más bajas, coeficientes de expansión de temperatura más altos y son más quebradizos [33]. Los materiales cristalinos, como el cuarzo, tienen las ventajas de ser más duros y tener una temperatura de fusión más alta [33].

Aplicaciones de Piezoelectricidad

Una serie de componentes eléctricos implican piezoelectricidad. Cuando se aplica un voltaje a través de una pieza de material piezoeléctrico, se dobla y deforma mecánicamente. Cuando se libera el voltaje, regresa a una frecuencia resonante natural. Este material se puede integrar con un circuito de retroalimentación para producir oscilaciones a una frecuencia precisa. Los osciladores eléctricos de este tipo suelen estar hechos de cuarzo cristalino. Una aplicación más reciente es el transformador piezoeléctrico. Estos dispositivos se utilizan en las lámparas fluorescentes de cátodo frío las cuales se utilizan como retroiluminación para paneles LCD [23, p. 289]. Las lámparas requieren alrededor de mil voltios para encenderse y cientos de voltios durante su uso. Los transformadores hechos de imanes y bobinas pueden lograr estos altos voltajes, pero los transformadores piezoeléctricos son mucho más pequeños, lo suficientemente pequeños como para montarse en una placa de circuito impreso. Un transformador tradicional involucra un par de bobinas, y convierte la electricidad de CA en energía magnética en electricidad de CA a un voltaje diferente. De manera similar, un transformador piezoeléctrico también implica múltiples procesos de conversión de energía. En dicho dispositivo, la electricidad de CA se convierte en vibraciones mecánicas y luego en electricidad de CA a un voltaje diferente. La energía se conserva en estos dispositivos, por lo que pueden producir altos voltajes con corrientes bajas. Figura\(\PageIndex{6}\): muestra un transformador piezoeléctrico que puede convertir una entrada de 8 a 14 V a una salida de hasta 2 kV [35]. Figura\(\PageIndex{7}\): muestra un ejemplo de algunos pequeños componentes de circuitos piezoeléctricos. Comenzando en la parte superior izquierda y yendo en sentido horario, se muestran un micrófono, un transmisor y receptor ultrasónicos, un sensor de vibración y un oscilador.

La eficiencia de los dispositivos de conversión de energía es difícil de discutir porque cada autor hace diferentes suposiciones. Sin embargo, por cualquier medida, la eficiencia de un dispositivo piezoeléctrico comercial es baja, a menudo 6% o menos [36]. Debido a esta baja eficiencia, muchos dispositivos piezoeléctricos se utilizan como sensores. Independientemente de esta baja eficiencia, se utilizan otros dispositivos para la recolección de energía. Por ejemplo, una estación de tren incorporó dispositivos piezoeléctricos en las plataformas para generar electricidad. También se han utilizado dispositivos piezoeléctricos para convertir la energía del movimiento de un fluido o del viento directamente a electricidad [36].

Figura\(\PageIndex{6}\): Transformador piezoeléctrico que toma una entrada de 8-14 V y produce y salida de hasta 2 kV. Esta foto es utilizada con permiso de [35].

Figura\(\PageIndex{7}\): Ejemplo de pequeños dispositivos piezoeléctricos. En sentido horario desde la parte superior izquierda: micrófono electret, sensor de distancia ultrasónico, sensor de vibración, cristal oscilador.

Existe interés en el uso de dispositivos piezoeléctricos para aplicaciones biomédicas. El cuarzo es piezoeléctrico y es duradero, fácilmente disponible y no tóxico. Los ingenieros han desarrollado dispositivos piezoeléctricos diseñados para su uso fuera del cuerpo y para ser implantados dentro del cuerpo. Algunos dispositivos piezoeléctricos se utilizan como sensores. Por ejemplo, los sensores piezoeléctricos pueden monitorear rodillas u otras articulaciones [3]. Además, la imagen ultrasónica es una técnica de diagnóstico común. Los dispositivos piezoeléctricos se utilizan tanto para generar las vibraciones ultrasónicas como para detectarlas [33]. Otros dispositivos piezoeléctricos biomédicos se utilizan como fuente de energía eléctrica. Los corazones artificiales, marcapasos y otros dispositivos requieren electricidad, y a menudo están limitados por la tecnología de batería disponible para abastecer la energía [36]. Los generadores piezoeléctricos no tienen partes móviles para desgastarse, y pueden evitar el problema de necesitar cambiar las baterías. La actividad física se puede clasificar como continua, como la respiración, o discontinua, como caminar. Ambos tipos de actividad física pueden ser utilizados como fuente de energía mecánica para dispositivos piezoeléctricos [36]. La cantidad de energía requerida para diferentes dispositivos biomédicos varía bastante. Por ejemplo, un corazón artificial puede requerir alrededor de 8 W mientras que un marcapasos puede requerir solo unos pocos microvatios [36]. Los dispositivos piezoeléctricos pueden capturar energía de la actividad física típica y convertirla en energía eléctrica para alimentar el dispositivo. Un dispositivo piezoeléctrico en una rodilla artificial ha producido 0.85 mW [36], y un dispositivo en un zapato ha generado 8.4 mW al caminar [36].

Los dispositivos piezoeléctricos se utilizan en otros tipos de sistemas de imágenes además de los sistemas de imágenes biomédicas. Una de las aplicaciones anteriores fue en sistemas de sonar. Alrededor de la época de la Primera Guerra Mundial, los militares desarrollaron activamente sistemas de sonar para detectar embarcaciones y submarinos. Hoy en día, los sistemas de sonar se utilizan para detectar peces y medir la profundidad de los cuerpos de agua [33]. También se utilizan imágenes de sonar para analizar circuitos eléctricos y detectar imperfecciones y grietas en acero y en soldaduras [33].

Los dispositivos piezoeléctricos también se utilizan en una variedad de otras aplicaciones. En algunos botones y teclados se utilizan sensores piezoeléctricos [36]. Los dispositivos piezoeléctricos se utilizan para hacer acelerómetros [37, p. 353], y se utilizan para medir el flujo de la tubería [33]. Los altavoces, micrófonos y zumbadores pueden estar hechos de dispositivos piezoeléctricos, y pueden funcionar tanto a frecuencias de audio como a frecuencias ultrasónicas. Los dispositivos piezoeléctricos que generan señales ultrasónicas se pueden utilizar para emulsionar tintes, pinturas y productos alimenticios como la mantequilla de maní [33]. También, se utilizan en algunas igniciones de parrillas de barbacoa donde el estrés mecánico induce una chispa eléctrica [23, ch. 15].