2.4: Problemas

2.1. Un condensador de placa paralela tiene una capacitancia de\(C =10 pF\). Las placas tienen área\(0.025 cm^2\). Una capa dieléctrica de espesor\(d_{thick} = 0.01 mm\) separa las placas. Para la capa dieléctrica, calcule la permitividad\(\epsilon\), la permitividad\(\epsilon_r\) relativa y la susceptibilidad eléctrica\(\chi_e\).

2.2. A menudo asumimos que la capacitancia de un condensador y la permitividad de un material son constantes. Sin embargo, a veces estas cantidades se describen mejor como funciones de frecuencia. Considere un condensador hecho de placas paralelas de área\(0.025 cm^2\) separadas por\(0.01 mm\). Supongamos que para\(\omega \lesssim 10^6 \frac{rad}{s}\), la capacitancia está bien modelada por\[C(\omega) = 8 \cdot 10^{-11} + 3 \cdot 10^{-15} \omega \nonumber \] en faradios. Para el material dieléctrico entre las placas del condensador, calcule la permitividad\(\epsilon(\omega)\), la permitividad\(\epsilon_r(\omega)\) relativa y la susceptibilidad eléctrica\(\chi_e(\omega)\).

2.3. Una galleta tipo sándwich cilíndrica tiene un radio de 0.75 pulg. La galleta está hecha de dos obleas, cada una de espesor de 0.15 pulgadas, las cuales son perfectas dieléctricas de permitividad relativa\(\epsilon_r =2.8\). Entre las obleas hay una capa de relleno de crema de espesor 0.1 en la que es un dieléctrico perfecto de permitividad relativa\(\epsilon_r =2.2\). Encuentra la capacitancia general de la cookie. Pista: Las capacitancias en serie se combinan como\(\frac{1}{\frac{1}{C_1}+\frac{1}{C_2}}\).

2.4. Un condensador de placa paralela tiene una capacitancia de\(3 \mu F\).

(a) Supongamos que otro condensador se fabrica utilizando el mismo material dieléctrico y con la misma área de sección transversal. Sin embargo, el grosor del dieléctrico entre las placas del condensador es el doble que el del condensador original. ¿Cuál es su capacitancia?

(b) Supongamos que un tercer condensador está hecho con la misma área de sección transversal y grosor que el primer condensador, pero a partir de un material con el doble de permitividad. ¿Cuál es su capacitancia?

2.5. Un material piezoeléctrico tiene una permitividad de\(\epsilon = 3.54 \cdot 10^{-11} \frac{F}{m}\) y tiene una constante de tensión piezoeléctrica de\(d =2 \cdot 10^{-10} \frac{m}{V}\). Si el material se coloca en un campo eléctrico de fuerza\(|\overrightarrow{E}| =70 \frac{V}{m}\) y se somete a una tensión de\(|\overrightarrow{\varsigma}| =3.5 \frac{N}{m^2}\). Calcular la polarización del material.

2.6. Un material piezoeléctrico tiene permitividad\(\epsilon_r = 2.5\). Si el material se coloca en un campo eléctrico de fuerza\(|\overrightarrow{E}| =2\cdot10^3\frac{V}{m}\) y se somete a una tensión de\(|\overrightarrow{\varsigma}| =200 \frac{N}{m^2}\), la polarización material del material es\(3.2 \cdot 10^{-8} \frac{C}{m^2}\). Calcular\(d\), la constante de deformación piezoeléctrica.

2.7. Considera dos dispositivos piezoeléctricos del mismo tamaño y forma. El material dieléctrico del primer dispositivo tiene una permitividad de\(\epsilon = 2.21 \cdot 10^{-11} \frac{F}{m}\) y una constante de tensión piezoeléctrica de\(d = 8 \cdot 10^{-11} \frac{m}{V}\). El material dieléctrico del segundo dispositivo tiene una susceptibilidad eléctrica\(chi_e =3.2\) y una constante de tensión piezoeléctrica de\(d = 2 \cdot 10^{-10} \frac{m}{V}\).

(a) Encontrar\(\epsilon_r\), la permitividad relativa, para cada dispositivo.

(b) Encontrar\(\frac{C_1}{C_2}\), la relación entre la capacitancia del primer dispositivo y la capacitancia del segundo dispositivo.

c) Los dispositivos se colocan en un campo eléctrico externo de fuerza\(|\overrightarrow{E}| =32 \frac{V}{m}\). No se pone tensión en los dispositivos. Calcular la polarización del material,\(\overrightarrow{P}\) para cada dispositivo.

d) Los dispositivos se colocan en un campo eléctrico externo de fuerza\(|\overrightarrow{E}| =32 \frac{V}{m}\), y\(|\overrightarrow{\varsigma}| =100 \frac{N}{m^2}\) se aplica una tensión de a los dispositivos. Calcular la polarización del material,\(\overrightarrow{P}\) para cada dispositivo.

(e) ¿Qué dispositivo esperarías que sea capaz de almacenar más energía? Explica tu respuesta.

2.8. Un dispositivo piezoeléctrico particular tiene un área de sección transversal de\(10^{-5} m^2\). Cuando\(800 \frac{N}{m^2}\) se aplica una tensión de, el dispositivo se comprime por\(10 \mu m\). Bajo estas condiciones, el dispositivo puede generar\(2.4 \cdot 10^{-9} J\). Calcular la eficiencia del dispositivo.

2.9. Un dispositivo piezoeléctrico particular tiene un área de sección transversal\(10^{-5} m^2\) y una eficiencia de 5%. Cuando\(1640 \frac{N}{m^2}\) se aplica una tensión de al dispositivo, oscila con una velocidad promedio de\(0.01 \frac{m}{s}\). Calcular la potencia que se puede generar desde el dispositivo.

2.10. Un dispositivo piezoeléctrico se coloca en un campo eléctrico de fuerza\(|\overrightarrow{E}| =500 \frac{V}{m}\). El dispositivo se prueba dos veces. En la primera prueba,\(|\overrightarrow{\varsigma}| =1000 \frac{N}{m^2}\) se puso una tensión de en el dispositivo, y se midió la polarización del material para ser\(|\overrightarrow{P}| =2.75 \cdot 10^{-8} \frac{C}{m^2}\). En la segunda prueba también con\(|\overrightarrow{E}| =500 \frac{V}{m}\),\(|\overrightarrow{\varsigma}| =100 \frac{N}{m^2}\) se puso una tensión de en el dispositivo, y se midió la polarización del material para ser\(|\overrightarrow{P}| =6.50 \cdot 10^{-9} \frac{C}{m^2}\). Encuentra la constante\(d\) de deformación piezoeléctrica y encuentra la permitividad relativa del material\(\epsilon_r\).

2.11. De acuerdo con la hoja de datos, un dispositivo piezoeléctrico es 3% eficiente. Un compañero de trabajo dice que la energía no se conserva en el dispositivo porque el 97% de la energía se pierde cuando se usa. Explica qué es lo que está mal con la explicación de tu compañero de trabajo.

2.12. Haga coincidir la propiedad del material con su definición. (No se usarán todas las definiciones).

1. Una tensión mecánica provocará una polarización (material) en este tipo de material.	A. Amorfo
2. Este tipo de material es vítreo y no cristalino.	B. Dieléctrico
3. Las cargas no fluyen fácilmente a través de este tipo de material	C. Ferroeléctrico
4. Ante la presencia de una tensión externa débil, las cargas no fluyen en este tipo de material. En presencia de un fuerte voltaje externo, las cargas fluyen fácilmente.	D. Piezoeléctrico
5. Una polarización material en un átomo induce polarización material en átomos cercanos en este tipo de material.

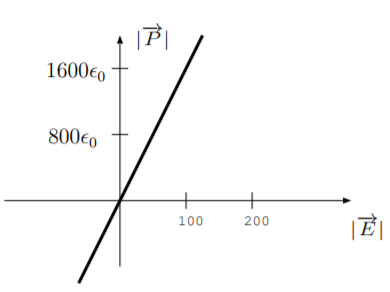
2.13. Considerar un material piezoeléctrico en un campo eléctrico externo\(\overrightarrow{E}\) en unidades V m. La figura muestra la magnitud de la polarización del material\(\frac{C}{m^2}\),\(|\overrightarrow{P}|\) en unidades, en función de la intensidad del campo eléctrico externo cuando no se aplica tensión mecánica. El material tiene una constante de deformación piezoeléctrica de\(d = 5 \cdot 10^{-10} \frac{m}{V}\).

a) Encontrar la permitividad\(\epsilon_r\) relativa y encontrar la susceptibilidad eléctrica\(\chi_e\).

(b) Encontrar y trazar una expresión para la magnitud de la polarización del material en función de la intensidad del campo eléctrico externo cuando\(1000 \frac{N}{m^2}\) se aplica una tensión de. Etiquete bien los ejes de su parcela.

(c) Este material se utiliza para hacer un dispositivo piezoeléctrico con un área de sección transversal de\(1 cm^2\). Cuando este dispositivo se comprime a una distancia de\(1 mm\),\(2 \cdot 10^{-10} J\) se almacena una energía de. Encuentra la eficiencia del dispositivo.

2.14. Considera la estructura cristalina 2D, mostrada en la figura, compuesta por una celosía y una base cristalina. La base cristalina está compuesta por dos átomos de tipo A y un átomo de tipo B.

(a) Esbozar la base cristalina.

(b) Esbozar la celosía 2D.

(c) Dibuja dos vectores primitivos\(\overrightarrow{a}_1\) y\(\overrightarrow{a}_2\) en tu boceto.

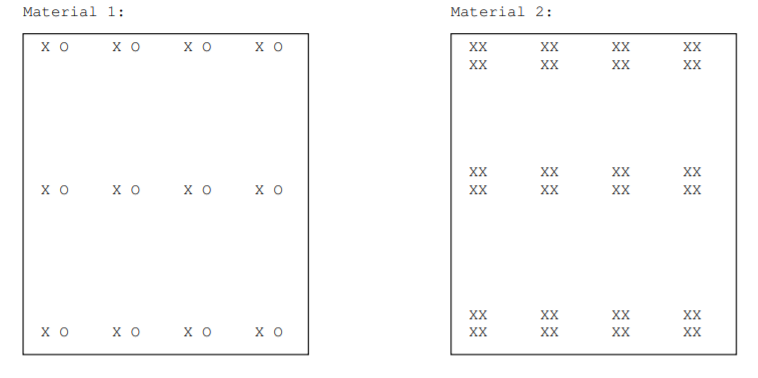
2.15. Considere las ilustraciones de la estructura cristalina de dos materiales 2D donde X y O representan la ubicación de diferentes tipos de átomos. ¿Los materiales tienen la misma estructura cristalina? base? celosía? grupo de puntos de cristal? Contesta sí o no, y explícale.

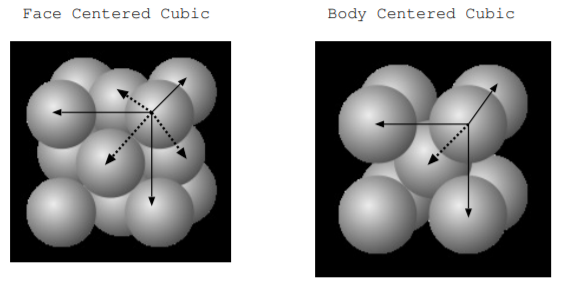
2.16. La siguiente figura ilustra dos posibles celosías cristalinas: una celosía cúbica centrada en la cara y una celosía cúbica centrada en el cuerpo. Las flechas sólidas representan vectores de celosía, pero no vectores de celosía primitivos, y las celdas mostradas no son celdas primitivas. Los vectores punteados en la figura muestran vectores de celosía primitivos. En el caso de la celosía cúbica centrada en la cara, los vectores primitivos de celosía van de un punto de esquina a un punto en el medio de una de las caras del cubo. En la celosía cúbica centrada en el cuerpo, los vectores primitivos de celosía van de un punto de esquina a un punto en el centro de una celda que bordea esa esquina. Supongamos que los vectores sólidos tienen longitud 0.4 nm. Encuentra la longitud del vector de celosía primitiva en la celosía cúbica centrada en la cara, y encuentra la longitud del vector de celosía primitiva en la celosía cúbica centrada en el cuerpo.