Saltar al contenido principal
LibreTexts Español

4.5: Problemas

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    81910

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    4.1. Una antena está diseñada para operar entre\(4.98 \text{ GHz}\) y\(5.02 \text{ GHz}\), para un ancho de banda de\( \Delta f = 0.04 \text{ GHz}\). Find\(\Delta \lambda\), el rango de longitud de onda sobre el cual la antena está diseñada para operar. Pista: La respuesta NO es 7.5 m.

    4.2. Usa la figura para encontrar la siguiente información. (Los cables que se conectan al receptor o transmisor no se muestran.)

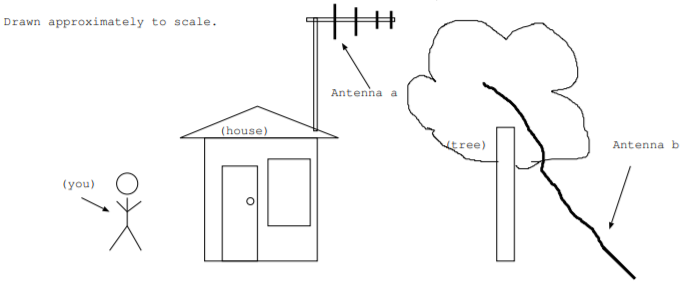
    4.5.1.png

    1. Aproximar la longitud de onda a la que la antena está diseñada para operar.
    2. Aproximar la frecuencia a la que la antena b está diseñada para operar.
    3. ¿Qué antena tiene probablemente elementos parásitos: antena a, antena b, ambas o ninguna? Explica tu elección.
    4. ¿Qué antena esperas que sea más isotrópica: antena a, antena b, o serían aproximadamente las mismas? Explica tu elección.
    5. ¿Qué antena es más probable que se utilice como receptor que como transmisor: antena a, antena b o ambas antenas aproximadamente iguales? Explica tu elección.

    4.3. Algunos especulan que las civilizaciones alienígenas podrían ser capaces de ver programas de televisión que escapan de la atmósfera terrestre. Para hacerse una idea de la probabilidad de que esto ocurra, considere una antena isotrópica en el espacio exterior que transmita una señal de\(200 \text{ MHz}\) TV.

    Supongamos que la civilización alienígena utiliza una antena con superficie\(0.5 m^2\) y cuenta con la tecnología para detectar una señal con potencia tan baja como\(5 \cdot 10^{-22} W\). ¿Cuál es la potencia mínima que se debe transmitir para que la detección ocurra a una distancia de 1.0 año luz?

    4.4. El Proyecto ELF, descrito en la Sec. 4.4.1, era un sistema de radio de frecuencia extremadamente baja establecido por los militares para comunicarse con submarinos.\(76 \text{ Hz}\) Tenía instalaciones cerca de Clam Lake, Wisconsin y Republic, Michigan, a 148 millas de distancia [52]. Debido a que estas instalaciones estaban ubicadas a una fracción de longitud de onda, las antenas en estas ubicaciones actuaron como parte de una sola matriz. La longitud de todos los elementos de la antena fue de 84 millas [52]. Supongamos que tardó 18 minutos en transmitir un mensaje de tres letras usando ASCII de 8 bits, y supongamos que las señales viajan cerca de la velocidad de la luz en el espacio libre.

    1. Calcular la relación de la distancia entre las instalaciones de transmisión y la longitud de onda.
    2. Calcular la relación entre la longitud de todos los elementos de la antena y la longitud de onda.
    3. ¿Cuál era la velocidad de comunicación en bits por segundo?
    4. ¿Cuántas longitudes de onda eran cada bit?

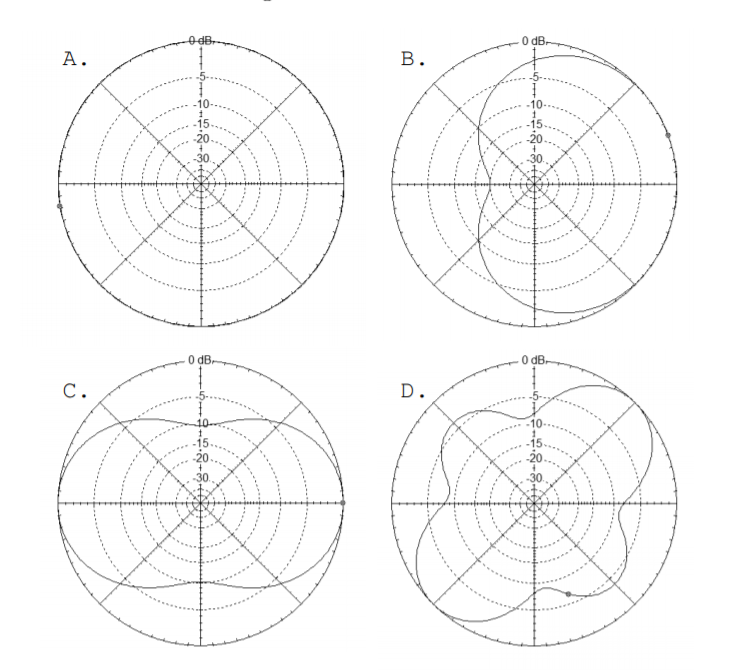
    4.5. Coincidir las siguientes parcelas o descripciones de antenas con sus parcelas de acimut.

    1. Una antena con gráfico 3D que se muestra a continuación

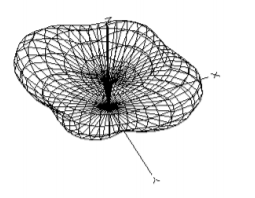
    4.5.2.png

    2. Una antena isotrópica

    3. Una antena con nulos en\(\pm 900\)

    4. Una antena con una ganancia de alrededor\(19 \text{dB}\)

    4.5.3.png

    4.6. Se muestran los gráficos del patrón de radiación para una antena de transmisión particular. Fueron trazados con EZNEC. La parcela acimutal está a la izquierda y la parcela de elevación a la derecha. La antena está diseñada para operar en\(360 \text{ MHz}\). Utilice las parcelas para responder a las siguientes preguntas.

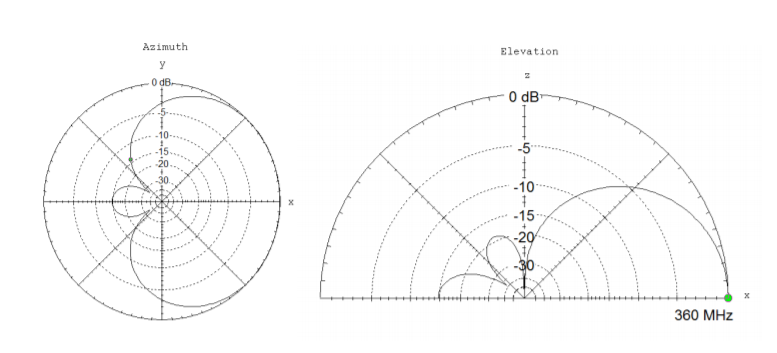
    4.5.4.png

    1. Supongamos que una persona a 100 m de distancia y que recibe la señal de la antena en la dirección frontal (a lo largo del\(\hat{a}_x\) eje) recibe una señal de 15 W. Aproximadamente, ¿qué tan fuerte de señal recibiría la persona al pararse a 100 m del transmisor a lo largo del\(\hat{a}_y\) eje (en vatios)?
    2. Encuentra el (poder)\(\text{F/B ratio}\) en\(\text{dB}\).
    3. De acuerdo con la gráfica acimutal, ¿en qué ángulo aproximadamente están los nulos para esta antena?
    4. ¿A qué longitud de onda está diseñada esta antena para operar?

    4.7. La Figura 4.4.2 muestra las gráficas del patrón de radiación para una antena cuádruple diseñada para operar en\(f = 21.2 \text{ MHz}\). La gráfica superior izquierda muestra la gráfica acimutal, la gráfica superior derecha muestra la gráfica de elevación. La gráfica inferior izquierda muestra el patrón de radiación 3D, y la gráfica inferior derecha muestra los elementos de la antena. Se trazaron con el software EZNEC.

    (a) Encuentre la longitud de onda a la que la antena está diseñada para operar.

    (b) Encontrar\(\left[\frac{|\overrightarrow{E}_{front}|}{|\overrightarrow{E}_{back}|}\right]_{dB}\), la relación de campo frontal a posterior de la antena en\(\text{dB}\).

    (c) Encontrar\(\left[\frac{|P_{front}|}{|P_{back}|}\right]_{dB}\), la relación de potencia delantera a trasera en\(\text{dB}\).

    (d) Encontrar\(\left[\frac{|P_{front}|}{|P_{back}|}\right]_{lin}\), la relación de potencia delantera a trasera en una escala lineal.

    (e) Supongamos que la intensidad del campo eléctrico a 50 m de distancia medida a lo largo del\(\phi = 45^{\circ}\) eje (en el\(z = 0\) plano) es\(5 \frac{V}{m}\). Encuentra la intensidad del campo eléctrico a 50 m de distancia medida a lo largo del\(\phi = 135^{\circ}\) eje (en el\(z = 0\) plano).

    4.8. Se muestran gráficos de patrón de radiación para una antena de transmisión particular. Fueron trazados con EZNEC. La parcela acimutal está a la izquierda y la parcela de elevación a la derecha.

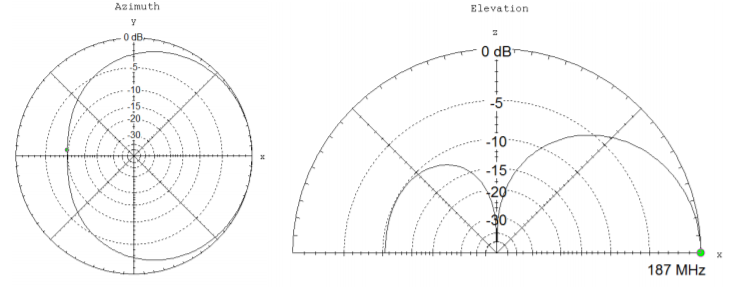
    4.5.5.png

    (a) ¿Esta antena es isotrópica? Justifica tu respuesta.

    (b) La antena está diseñada para operar a una frecuencia de\(187 \text{ MHz}\). ¿Cuál es la longitud de onda correspondiente?

    (c) Encontrar el (poder)\(\text{F/B ratio}\) en\({dB}\).

    (d) La señal a 100 m de la antena transmisora en la dirección frontal (\(\phi = 0\)) se mide para ser\(|\overrightarrow{E}| = 50 \frac{V}{m}\). ¿Cuál es la intensidad del campo eléctrico de la señal\(\frac{V}{m}\) a 100 m de la antena en la\(\phi = 45^{\circ}\) dirección?

    e) Las gráficas de patrones de radiación no se aplican a todas las distancias desde la antena. ¿Aproximadamente para qué distancias de distancia son válidas las parcelas de radiación?

    4.9. Determine si las siguientes ondas electromagnéticas están polarizadas linealmente, polarizadas circularmente derecha, polarizadas circularmente izquierda, polarizadas elípticamente derecha o polarizadas elípticamente izquierda. Todas estas olas viajan en la\(\hat{a}_z\) dirección, y\(\omega\) es una constante. (Esta es una versión modificada de P3.34 de [11].)

    (a)\(\overrightarrow{E} =10\cos(\omega t - 8z) \hat{a}_x + 10\sin(\omega t - 8z) \hat{a}_y\)

    b)\(\overrightarrow{E} =10\cos(\omega t - 8z) \hat{a}_x + 10\sin(\omega t - 8z) \hat{a}_y\)

    c)\(\overrightarrow{E} =10\cos(\omega t - 8z + \frac{\pi}{4}) \hat{a}_x + 20\sin(\omega t - 8z + \frac{\pi}{4}) \hat{a}_y\)

    d)\(\overrightarrow{E} =10\cos(\omega t - 8z) \hat{a}_x - 10\sin(\omega t - 8z) \hat{a}_y\)

    This page titled 4.5: Problemas is shared under a CC BY-NC 4.0 license and was authored, remixed, and/or curated by Andrea M. Mitofsky via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.