5.1: Física del efecto Hall

Los dispositivos de efecto Hall son dispositivos de conversión de energía directa que convierten la energía de un campo magnético en electricidad. La física detrás de estos dispositivos se describe mediante la ecuación de fuerza de Lorentz. Esta discusión sigue las referencias [3] y [9]. Si colocamos una carga en un campo eléctrico externo, se sentirá una fuerza paralela al campo eléctrico aplicado. Si colocamos una carga móvil en un campo magnético externo, sentirá una fuerza perpendicular al campo magnético aplicado. La ecuación de fuerza de Lorentz\[\overrightarrow{F} = Q\left(\overrightarrow{E} + \overrightarrow{v} \times \overrightarrow{B} \right) \nonumber \]

describe las fuerzas sobre la carga móvil debidas a los campos eléctricos y magnéticos externos. En la ecuación anterior,\(\overrightarrow{F}\) representa la fuerza en newtons sobre una carga que se mueve con velocidad\(\overrightarrow{v}\) en unidades\(\frac{m}{s}\). La cantidad\(\overrightarrow{E}\) representa la intensidad del campo eléctrico en unidades\(\frac{V}{m}\), y\(\overrightarrow{B}\) representa la densidad de flujo magnético en unidades\(\frac{Wb}{m^2}\). La carga en culombios se denota por\(Q\). Observe que la fuerza sobre la carga debida al campo eléctrico apunta en la misma dirección que el campo eléctrico mientras que la fuerza sobre la carga debida al campo magnético apunta perpendicularmente tanto a la velocidad de la carga como a la dirección del campo magnético.

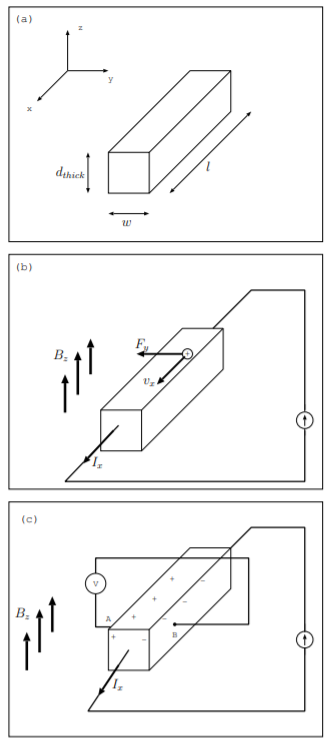
El efecto Hall ocurre tanto en conductores como en semiconductores. En los conductores, los electrones son los portadores de carga responsables del efecto mientras que en los semiconductores, tanto los electrones como los huecos son los portadores de carga responsables del efecto [9]. Un agujero es la ausencia de un electrón. Considere una pieza de semiconductor orientada como se muestra en la Fig. \(\PageIndex{1}\)a. Supongamos que la longitud está especificada por\(l\), se especifica\(w\) el ancho y el grosor se especifica por\(d_{thick}\). Para un dispositivo típico de efecto Hall, estas dimensiones pueden estar en el rango milimétrico. Además, supongamos que el semiconductor es de tipo p con concentración de agujeros\(p\) en unidades\(m^{-3}\). La concentración de carga representa la densidad de carga neta, o en exceso, por encima de un material neutro. Los materiales con una carga negativa neta, exceso de electrones de valencia, tendrán un valor positivo para la concentración de electrones\(n\) y se denominan tipo n. Los materiales con una carga positiva neta, un exceso de agujeros, tendrán un valor positivo para la concentración de agujeros\(p\) que representa la densidad de agujeros en el material y se denominan tipo p. La densidad de carga total está relacionada con\(n\) y\(p\) por\[\rho_{ch} = -qn + qp \nonumber \]

donde\(q\) está la magnitud de la carga de un electrón.

Supongamos que el semiconductor se coloca en un campo magnético externo orientado en la\(\hat{a}_z\) dirección, con densidad de flujo magnético\[\overrightarrow{B} = B_z\hat{a}_z. \nonumber \]

También supongamos que se suministra una corriente a través del semiconductor en la\(\hat{a}_x\) dirección. Los portadores de carga positiva en el semiconductor, agujeros, se mueven con velocidad\(\overrightarrow{v} = v_x\hat{a}_x\) porque la corriente es el flujo de carga por unidad de tiempo. Estas medidas se ilustran en la Fig. \(\PageIndex{1}\)b. Los dispositivos de efecto Hall se utilizan normalmente como sensores a diferencia de los dispositivos de recolección de energía porque la energía debe suministrarse a partir de esta corriente externa y porque la cantidad de electricidad producida suele ser bastante pequeña.

La fuerza sobre las cargas se puede encontrar a partir de la ecuación de fuerza de Lorentz. La fuerza debida al campo magnético externo sobre una carga de magnitud\(q\) viene dada por

\[q\overrightarrow{v} \times \overrightarrow{B} = qv_x\hat{a}_x \times B_z\hat{a}_z = -qB_z\hat{a}_y \nonumber \]

y se orienta en la\(-\hat{a}_y\) dirección. Las cargas positivas se acumulan en un lado del semiconductor como se muestra en la Fig. \(\PageIndex{1}\)c. Esta acumulación de carga provoca un campo eléctrico orientado en la\(\hat{a}_y\) dirección que se opone a una mayor acumulación de carga. Las cargas se acumulan hasta que se alcanza un equilibrio cuando las fuerzas sobre las cargas en la\(\hat{a}_y\) dirección son cero.

\[\overrightarrow{F} = 0 = Q\left(\overrightarrow{E} + \overrightarrow{v} \times \overrightarrow{B} \right) \nonumber \]

Figura\(\PageIndex{1}\): Ilustración del efecto Hall.

La intensidad del campo eléctrico se puede expresar como una función del voltaje\(V_{AB}\) medido a través del ancho del dispositivo, en la\(\hat{a}_y\) dirección.

\[\overrightarrow{E} = \frac{V_{AB}}{w}\hat{a}_y \nonumber \]

\[q\overrightarrow{E} = -q\overrightarrow{v} \times \overrightarrow{B} \nonumber \]

\[\frac{V_{AB}}{w} = v_xB_z \label{5.1.8} \]

Si bien a menudo\(v_x\) se desconoce la magnitud de la velocidad de las cargas\(I_x\), se conoce la corriente aplicada, en unidades amperios. La densidad de corriente a través de una sección transversal del dispositivo es el producto de la concentración de carga, la fuerza de las cargas y la velocidad de las cargas.

\[\text{current density} = \frac{I_x}{w \cdot d_{thick}} = q \cdot v_x \cdot p \nonumber \]

A partir de la expresión anterior, la velocidad se puede expresar en términos de la corriente.

\[v_x = \frac{I_x}{w \cdot d_{thick} \cdot q \cdot p} \label{5.1.10} \]

Las ecuaciones\ ref {5.1.8} y\ ref {5.1.10} se pueden combinar.

\[V_{AB} = \frac{w \cdot I_x \cdot B_z}{w \cdot d_{thick} \cdot q \cdot p} \nonumber \]

Un magnetómetro es un dispositivo que mide el campo magnético. Para usar un dispositivo de efecto Hall como magnetómetro, comience con una pieza de semiconductor de dimensiones conocidas y concentración de carga conocida, y luego aplique una corriente. Si se mide el voltaje perpendicular a la corriente, se puede calcular el campo magnético. El voltaje medido es proporcional a la fuerza de la densidad de flujo magnético externo.

\[B_z = \frac{d_{thick} \cdot q \cdot p \cdot V_{AB}}{I_x} \nonumber \]

El voltaje se mide fácilmente con un voltímetro, por lo que no se necesitan herramientas especializadas. Para medir de manera confiable este voltaje, a menudo se amplifica.

Alternativamente, si se conoce la intensidad de un campo magnético externo, se puede usar el efecto Hall para medir las concentraciones de agujeros o electrones en una pieza de semiconductor. Con algo de álgebra, podemos escribir la concentración de agujeros en función de las dimensiones del semiconductor, la intensidad del campo magnético conocida, la corriente aplicada y el voltaje medido.

\[p = \frac{I_x \cdot B_z}{d_{thick} \cdot q \cdot V_{AB}} \label{5.1.13} \]

Se puede encontrar una expresión análoga si los electrones en lugar de agujeros son el portador de carga dominante. El signo de esta tensión medida también se utiliza para determinar si una pieza de semiconductor es de tipo n o de tipo p [58].

La resistencia Hall\(R_H\) es un parámetro inversamente proporcional a la concentración de carga, y tiene las unidades de ohmios [9] [59]. Para los supuestos anteriores, la resistencia Hall se define como

\[R_H = \frac{B_z}{qp} \cdot \frac{w}{l \cdot d_{thick}}. \label{5.1.14} \]

Al combinar las Ecuaciones\ ref {5.1.13} y\ ref {5.1.14}, se puede escribir en términos de la tensión medida y la corriente aplicada.

\[R_H = \frac{V_{AB}}{I_x} \cdot \frac{w}{l} \nonumber \]

Como ejemplo, supongamos que una pieza de silicio con una concentración de agujeros de\(p = 10^{17} cm^{-3}\) se utiliza como dispositivo de efecto Hall. El dispositivo tiene dimensiones\(l = 1 cm\),\(w = 0.2 cm\), y\(d_{thick} = 0.2 cm\), y está orientado como se muestra en la Fig. \(\PageIndex{1}\). El material tiene una resistividad de\(\rho = 0.9 \Omega \cdot cm\). Se\(I = 1 mA\) aplica una corriente de en la\(\hat{a}_x\) dirección. El dispositivo se encuentra en un campo magnético externo de\(\overrightarrow{B} = 10^{-5}\hat{a}_z \frac{Wb}{cm^2}\). Si se conecta un voltímetro como se muestra en la figura, ¿qué voltaje\(V_{AB}\) se mide?

\[V_{AB} = \frac{I_x \cdot B_z}{q \cdot d_{thick} \cdot p} = \frac{1^{-3} \cdot 10^{-5}}{1.6 \cdot 10^{-19} \cdot 0.2 \cdot 10^{17}} = 3.1 \cdot 10^{-6} V \nonumber \]

Las señales en el rango de milivoltios se detectan fácilmente con un voltímetro estándar, sin embargo, las señales en el rango de microvoltios a menudo se pueden medir con alguna amplificación. ¿Qué potencia de salida genera este dispositivo? Podemos calcular la resistencia a lo largo de la\(\hat{a}_y\) dirección. La resistividad del silicio se dio en el problema, y la resistencia\(R\) y resistividad\(\rho\) están relacionadas por

\[R = \frac{\rho \cdot \text{length}}{\text{area}}. \nonumber \]

La resistencia a través del ancho del dispositivo es

\[R_{width} = \frac{\rho w}{ld_{thick}} = \frac{0.09 \cdot 0.2}{1 \cdot 0.2} = 0.09 \Omega \nonumber \]

Podemos utilizar esta resistencia calculada y el voltaje medido para encontrar la potencia convertida del campo magnético a la energía eléctrica del dispositivo.

\[P = \frac{V^2_{AB}}{R_{width}} = 1.1 \cdot 10^{-11} W \nonumber \]

Esta cantidad de poder es pequeña. Si bien este dispositivo puede hacer un sensor útil, no hará un dispositivo de recolección de energía útil. Genera decenas de picovatios de potencia, y se debe suministrar una\(1 mA\) corriente para generar la energía.