6.3: Cristalografía revisitada
- Page ID
- 81924
Espacio Real y Espacio Recíproco
Los físicos y químicos suelen estar interesados en dónde es probable que se encuentren electrones o nucleones de átomos con respecto a la posición en el espacio real. Las ideas de una celosía, base y estructura cristalina se discutieron en la Sec. 2.3.2. Para revisar, una celosía describe las disposiciones de los puntos. La base describe cómo se disponen los átomos en cada punto de celosía. La celosía y la base juntas forman la estructura cristalina. Una red 3D es descrita por tres vectores de celosía\(\overrightarrow{a_1}\),\(\overrightarrow{a_2}\), y\(\overrightarrow{a_3}\). Si se eligen lo más cortos posible, se les llama vectores de celosía primitivos. La magnitud de un vector reticular primitivo puede ser de alrededor de 0.1 nm. Los vectores de celosía primitivos definen una celda llamada celda primitiva. Dado que una celosía es periódica, si sabemos describir una celda primitiva, podemos describir toda la celosía.
Para cada celosía, existe una red recíproca correspondiente definida por un conjunto de vectores. Ambos contienen la misma información en diferentes formas. Para una red 3D con vectores primitivos\(\overrightarrow{a_1}\),\(\overrightarrow{a_2}\), y\(\overrightarrow{a_3}\), los vectores de la red recíproca son etiquetados por los vectores\(\overrightarrow{b_1}\),\(\overrightarrow{b_2}\), y\(\overrightarrow{b_3}\).
\[\overrightarrow{b_1} = \frac{2 \pi \overrightarrow{a_2} \times \overrightarrow{a_3}}{\overrightarrow{a_1} \cdot \overrightarrow{a_2} \times \overrightarrow{a_3}} \nonumber \]
\[\overrightarrow{b_2} = \frac{2 \pi \overrightarrow{a_3} \times \overrightarrow{a_1}}{\overrightarrow{a_1} \cdot \overrightarrow{a_2} \times \overrightarrow{a_3}} \nonumber \]
\[\overrightarrow{b_3} = \frac{2 \pi \overrightarrow{a_1} \times \overrightarrow{a_2}}{\overrightarrow{a_1} \cdot \overrightarrow{a_2} \times \overrightarrow{a_3}} \nonumber \]
Observe que\(\overrightarrow{b_1}\) es perpendicular a\(\overrightarrow{a_2}\) y\(\overrightarrow{a_3}\). También,\(\overrightarrow{b_1}\) es paralelo a\(\overrightarrow{a_1}\). Más específicamente,\( |\overrightarrow{b_1}| \cdot |\overrightarrow{a_1}| = 2 \pi\). (Factores de\(2 \pi \) presentación por elección de unidades,\(\frac{cycles}{m}\) vs\(\frac{rad}{m}\).) Por lo tanto, si vector\(\overrightarrow{a_1}\) es largo,\(\overrightarrow{b_1}\) será corto. Así como podemos llegar de un punto de celosía a otro viajando múltiplos enteros de los vectores de\(\overrightarrow{a_\mathfrak{n}}\) celosía, podemos obtener de cualquier punto al siguiente de la red recíproca viajando múltiplos enteros del vector de\(\overrightarrow{b_\mathfrak{n}}\) celosía. Los vectores de celosía en el espacio real tienen unidades de longitud,\(m\). Los vectores de celosía en el espacio recíproco tienen unidades\(m^{-1}\).
La red recíproca da información sobre la frecuencia espacial de los átomos. Si los planos de los átomos en un cristal están estrechamente espaciados en una dirección,\(|\overrightarrow{a_1}|\) es relativamente pequeño. El vector recíproco correspondiente\(|\overrightarrow{b_1}|\) es relativamente grande. La red recíproca representa la frecuencia espacial del átomo en unidades\(m^{-1}\). Si los planos de átomos en un cristal están muy separados,\(|\overrightarrow{a_1}|\) es grande y\(|\overrightarrow{b_1}|\) es pequeño.
Si un haz de luz brilla sobre un cristal donde la longitud de onda de la luz está cerca del espaciamiento entre los cristales, la luz se difractará y el patrón de difracción se relaciona con la red recíproca. La zona Brillouin es una celda primitiva para una red recíproca. El volumen de una celda unitaria en el espacio recíproco sobre una celda unitaria en el espacio real viene dado por
\[\frac{\text{vol. Brillouin zone}}{\text{vol. primitive cell in real space}} = \frac{\overrightarrow{b_1} \cdot \overrightarrow{b_2} \times \overrightarrow{b_3}}{\overrightarrow{a_1} \cdot \overrightarrow{a_2} \times \overrightarrow{a_3}} =(2\pi)^3. \nonumber \]
En cuanto a la celosía espacial real, para entender la celosía espacial recíproca, solo necesitamos entender una celda porque la celosía espacial recíproca es periódica.
versus k Diagramas
Los diagramas de nivel de energía, discutidos en la Sección 6.2, trazaron energías de electrones donde el eje vertical representaba energía. No se muestran variaciones en el eje horizontal. Los diagramas de nivel de energía más útiles para semiconductores se amplían de manera que solo se muestran la valencia y la banda de conducción. En muchos casos, es útil trazar diagramas de nivel de energía versus posición en el espacio real. Para tal diagrama, el eje vertical representa la energía, y el eje horizontal representa la posición. También es útil para trazar diagramas de nivel de energía versus posición en el espacio recíproco.
La energía cinética viene dada por
\[E_{kinetic} = \frac{1}{2}m|\overrightarrow{v}|^2 = \frac{1}{2m}|\overrightarrow{M}|^2 \nonumber \]
donde\(\overrightarrow{v}\) representa la velocidad en\(\frac{m}{s}\) y\(m\) representa la masa en kg. El impulso viene dado por\(\overrightarrow{M} = m\overrightarrow{v}\) en unidades\(\frac{kg \cdot m}{s} = \frac{J \cdot s}{m}\). Los electrones en los cristales a\(T > 0\) K vibran, y ciertas vibraciones son resonantes en el cristal. El impulso cristalino\(\overrightarrow{M}_{crystal}\) representa el impulso interno de debido a las vibraciones. Se puede expresar como
\[\overrightarrow{M}_{crystal} = \hbar\overrightarrow{k} \nonumber \]
y tiene unidades de impulso\(\frac{kg \cdot m}{s}\). A la cantidad\(\overrightarrow{k}\) se le llama vector de onda, y tiene unidades\(m^{-1}\). Representa un cambio en la frecuencia espacial, una distancia en el espacio recíproco. La constante
\[\hbar = \frac{h}{2\pi} \nonumber \]
se llama h-bar y es la constante de Planck dividida por\(2\pi\). La energía cinética se puede escribir en términos del vector de onda.
\[E_{kinetic} = \frac{\hbar^2 |\overrightarrow{k}|^2}{2m} \label{6.3.8} \]
La ecuación\ ref {6.3.8} describe cómo la energía de un electrón varía con el vector de onda\(|\overrightarrow{k}|\) que incorpora información sobre las vibraciones de la red. La energía es cuadrática en el vector de onda, por lo que las gráficas de energía versus\(|\overrightarrow{k}|\) son parabólicas. La ecuación\ ref {6.3.8} es solo un modelo, y se aplica mejor cerca de la parte superior de la banda de valencia y la parte inferior de la banda de conducción.
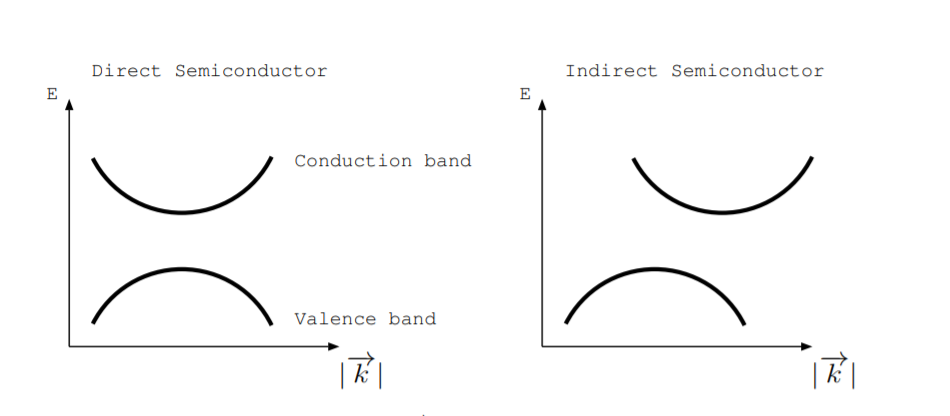
La gráfica de energía versus\(|\overrightarrow{k}|\) diagramas permitió niveles de energía. Piense en el\(|\overrightarrow{k}|\) eje como cambio de posición en el espacio recíproco. Si la parte superior de la banda de valencia y la parte inferior de la banda de conducción ocurren al mismo\(|\overrightarrow{k}|\) valor en un semiconductor, decimos que es directa. Si la parte superior de la banda de valencia y la parte inferior de la banda de conducción ocurren a diferentes\(|\overrightarrow{k}|\) valores, decimos que el semiconductor es indirecto. La parte izquierda de la Fig. \(\PageIndex{1}\)muestra un\(|\overrightarrow{k}|\) diagrama de energía versus para un semiconductor directo, y la parte derecha de la Fig. \(\PageIndex{1}\)muestra uno para un semiconductor indirecto. GaAs, InP y ZnTe son semiconductores directos. Si, Ge, AlAs y GaP son semiconductores indirectos. A lo largo de diferentes ejes cristalinos, la estructura de la banda cambia algo. El eje horizontal de una energía versus\(|\overrightarrow{k}|\) diagrama puede especificarse a lo largo de un eje particular en el espacio recíproco.
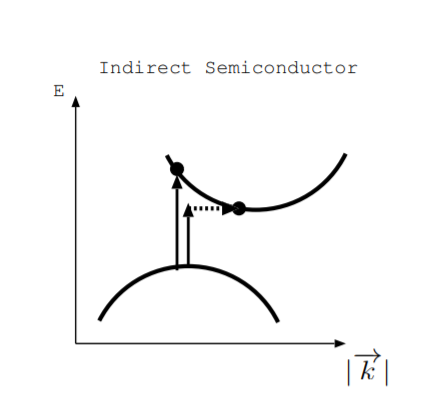
¿Qué sucede cuando iluminamos un semiconductor directo? Un fotón de suficiente energía puede excitar un electrón de la banda de valencia a la banda de conducción para crear un par electrón-hueco. ¿Qué sucede en un semiconductor indirecto? La figura\(\PageIndex{2}\) ilustra dos posibilidades. Como lo ilustra la flecha más larga, un electrón puede excitarse directamente desde la valencia a la banda de conducción. Sin embargo, esto requiere un fotón de más energía que la distancia vertical entre la parte superior de la banda de valencia y la parte inferior de la banda de conducción [25, p. 200]. Alternativamente, como se ilustra por las otras dos flechas, la excitación desde la parte superior de la banda de valencia hasta la parte inferior de la banda de conducción puede implicar un fotón y un fonón. Tanto la energía como el impulso deben conservarse, por lo que se necesita un cambio en el impulso cristalino para excitar un electrón en este caso. Las células solares y los fotodetectores pueden estar hechos de semiconductores directos o indirectos.