6.4: pn Juncciones
- Page ID
- 81923
Muchos dispositivos, incluidos los dispositivos fotovoltaicos, LEDs, fotodiodos, láseres semiconductores y dispositivos termoeléctricos, están hechos esencialmente de uniones pn. Para entender los dispositivos fotovoltaicos y estos otros dispositivos de conversión de energía, necesitamos entender las uniones pn. Considera un cristal semiconductor compuesto por un material tipo n (con exceso de electrones) en un lado y un material tipo p (carente de electrones, en otras palabras, con exceso de agujeros) en el otro lado. La unión de los materiales tipo p y tipo n se denomina unión pn. Supongamos que la unión es abrupta y se encuentra en equilibrio térmico.
Algunas uniones pn están hechas de semiconductores elementales como Si, y otras uniones pn están hechas de semiconductores compuestos como GaAs.
Algunas uniones pn tienen el mismo material en ambos lados, mientras que otras uniones pn tienen diferentes materiales en cada lado. Por ejemplo, una unión pn se puede hacer a partir de una capa de tipo n de GaAs y una capa de tipo p de GaAs. También se puede hacer a partir de una capa de GaAs tipo n y una capa de tipo p de AlAS.
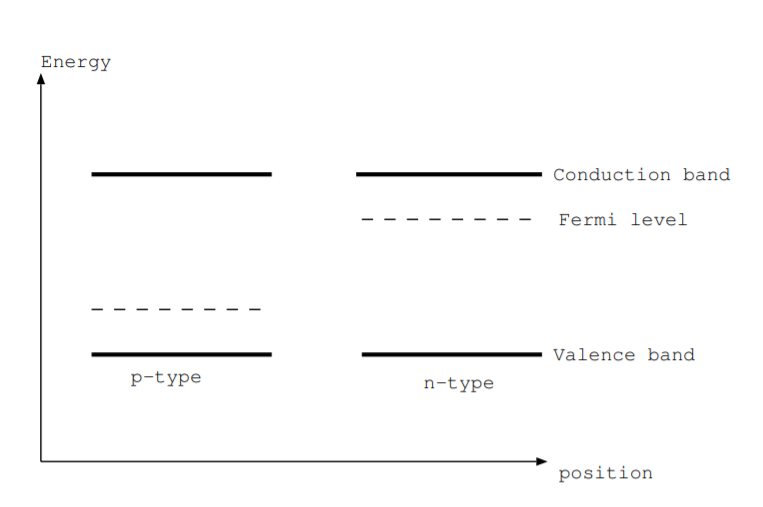
¿Qué sucede cuando juntamos un material tipo p y un material tipo n para formar una unión pn? Los electrones de valencia y los agujeros se mueven. Los núcleos y los electrones de la capa interna no lo hacen. Algunos electrones sobrantes de la región tipo n van hacia la región de tipo p. Algunos agujeros sobrantes de la región tipo p van hacia la región de tipo n. Estos portadores de carga difunden, son barridos de, una región cercana al cruce. Esta región cercana a la unión que carece de portadores de carga se denomina capa de agotamiento [10, p. 564]. Como se muestra en la Fig. \(\PageIndex{1}\), el nivel Fermi\(E_f\) está cerca de la banda de valencia para materiales tipo p. El material tipo P carece de electrones, por lo que la energía donde es igualmente probable que encuentre un estado electrónico ocupado y desocupado está más cerca de la banda de valencia. Por una razón similar, el nivel de Fermi\(E_f\) se encuentra cerca de la banda de conducción para materiales tipo n. La figura\(\PageIndex{2}\) muestra el diagrama de nivel de energía versus posición para la unión pn, y los niveles de Fermi de los dos materiales están alineados en esta figura.
Considere una unión donde el material de tipo n es silicio dopado con átomos de fósforo y el material de tipo p es silicio dopado con átomos de aluminio. El lado tipo n de la unión pn tiene un exceso de cargas positivas debido a que algunos átomos de fósforo reemplazan a los átomos de Si en el material. Los átomos de fósforo tienen un protón más que los átomos de silicio. También tienen un electrón más, pero el electrón de valencia es un portador de carga que se difunde lejos de la unión. De manera similar, el lado tipo p de la unión tiene un exceso de cargas negativas debido a que algunos átomos de aluminio reemplazan a los átomos de silicio. Los átomos de aluminio tienen un protón menos que los átomos de Si. También tienen un electrón menos, pero el agujero es un portador de carga que también se difunde lejos de la unión.
Se forma un campo eléctrico a través de la unión debido a la distribución neta de carga cerca del cruce. La intensidad del campo eléctrico es la fuerza por unidad de carga, y tiene las unidades\(\frac{V}{m}\). También hay necesariamente una caída de voltaje a través de una unión pn en equilibrio, y esta tensión se denomina potencial de contacto\(V_0\) en las unidades de voltios. Si bien el potencial de contacto es un voltaje, no se puede medir colocando un voltímetro a través de una unión pn porque se formarían uniones adicionales en cada cable del voltímetro con voltajes adicionales introducidos [9, p. 141].
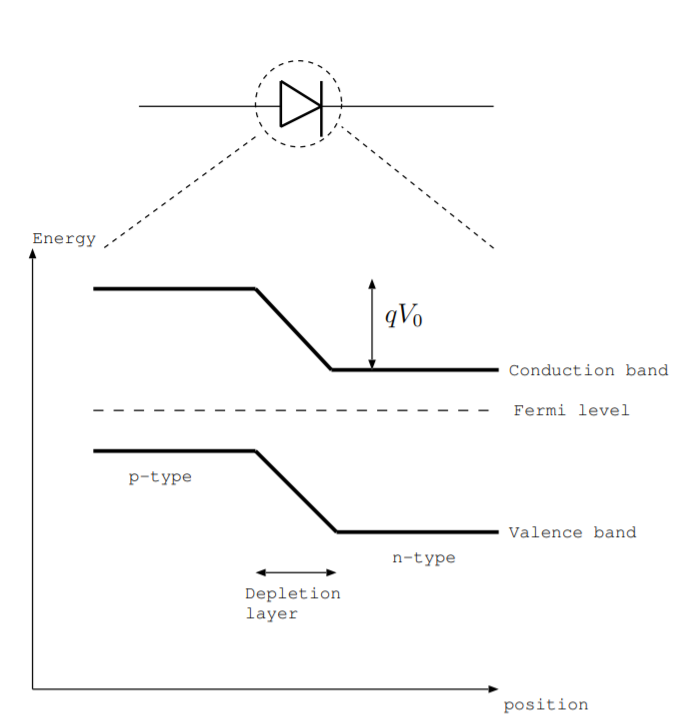
La figura\(\PageIndex{2}\) ilustra el diagrama de nivel de energía de una unión pn. El eje horizontal representa la posición, y el eje vertical representa la energía. Se relaciona con las cifras de la Sección 6.2. Sin embargo, la Fig. \(\PageIndex{2}\)se amplía verticalmente, y se traza versus posición cerca del cruce. También muestra la relación entre el diagrama de nivel de energía y el símbolo de circuito para un diodo, y la capa de agotamiento está etiquetada. La distancia vertical\(qV_0\), también etiquetada en la Fig. \(\PageIndex{2}\), representa la cantidad de energía requerida para mover un electrón a través de la unión [9, p. 141].
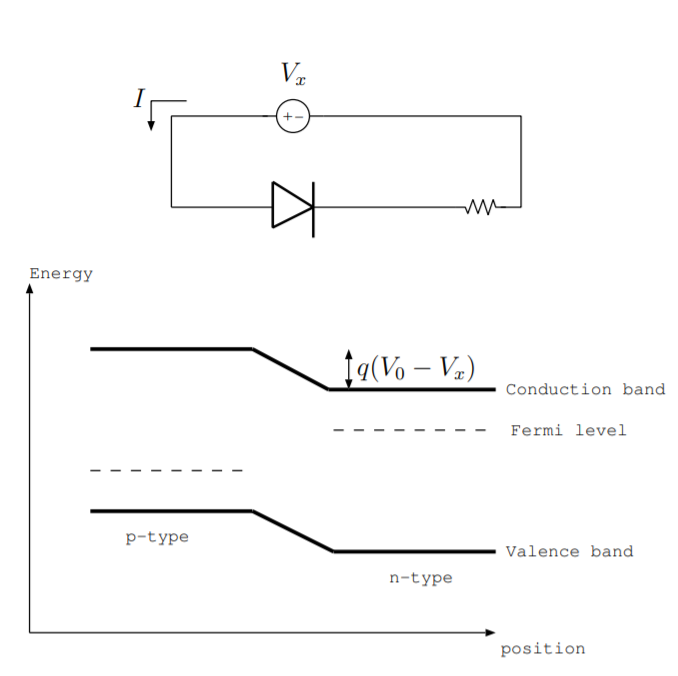
La figura\(\PageIndex{3}\) muestra el diagrama de nivel de energía para una unión pn polarizada hacia delante. En una unión pn con polarización directa, la corriente fluye desde el lado de tipo p a tipo n de la unión. Más específicamente, los orificios fluyen de la región de tipo p a tipo n, y algunos de estos orificios neutralizan las cargas excedentes en la capa de agotamiento. La capa de agotamiento se vuelve más estrecha. El campo eléctrico que impide el flujo de cargas se hace más pequeño, y la caída de voltaje a través de la unión se vuelve más pequeña. La energía\(q (V_0 - V_x)\) está etiquetada en la Fig. \(\PageIndex{3}\)para una unión pn polarizada hacia delante donde el voltaje\(V_x\) es el voltaje suministrado. Esta energía representa la energía necesaria para que las cargas fluyan a través de la unión, y es más pequeña que la energía correspondiente en el caso de la unión imparcial. Las cargas fluyen más fácilmente en el caso de una unión pn polarizada hacia delante, y el diodo actúa como un cable.
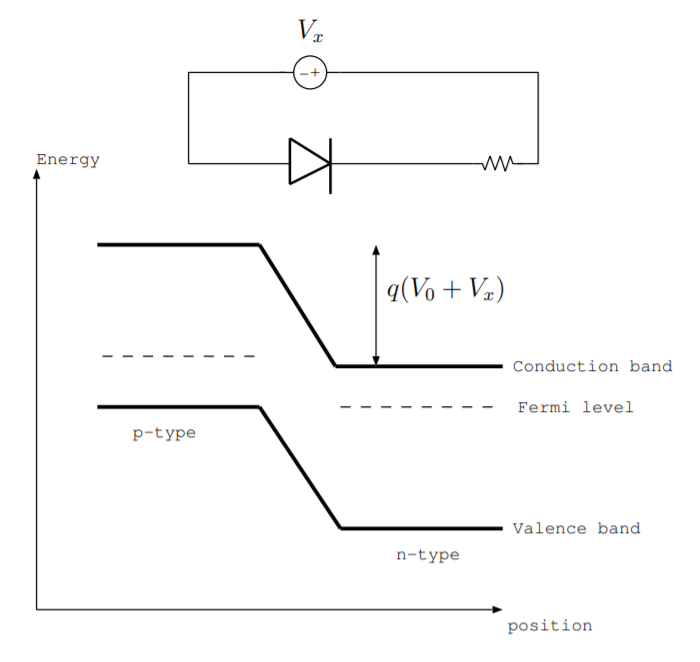
La figura\(\PageIndex{4}\) muestra el diagrama de nivel de energía para una unión pn polarizada invertida. Para una unión pn polarizada inversa, la tensión a través de la unión\(V_0 + V_x\) es mayor que para una unión no polarizada, y la energía necesaria para que fluyan las cargas\(q (V_0 + V_x)\) es mayor que para una unión no polarizada. Las uniones pn polarizadas invertidas actúan como circuitos abiertos, y las cargas no fluyen debido a esta cantidad de energía requerida.
Un diodo emisor de luz (LED) es un dispositivo que convierte la electricidad en energía electromagnética óptica, y está hecho de una unión pn semiconductora. En uso, se coloca una polarización hacia delante a través del LED como se muestra en la Fig. \(\PageIndex{3}\). Los agujeros fluyen desde la región de tipo p a tipo n. Algunos de estos agujeros se combinan con electrones en la capa de agotamiento. En un LED, se emiten fotones en este proceso. La energía del fotón emitido corresponde a la energía de la brecha de energía. Algunos LEDs tienen una capa intrínseca adicional, no dopada, en la unión, entre las capas tipo p y tipo n para mejorar la eficiencia del dispositivo.
Una célula solar y un fotodetector óptico también son esencialmente uniones pn. Ambos dispositivos convierten la energía electromagnética óptica en electricidad. Cuando la luz brilla en estos dispositivos, se crean pares electrón-agujero en la unión. Debido a la distribución de carga a través de la unión, muchos de los electrones y agujeros creados son barridos lejos de la unión antes de que puedan recombinarse [9]. Este flujo de cargas es una corriente, por lo que la energía electromagnética óptica se convierte en electricidad. Cuando la luz brilla en un dispositivo fotovoltaico, se puede medir una tensión a través de la unión, y este efecto se denomina efecto fotovoltaico [9, p. 212].
La distancia vertical entre la banda de conducción y la banda de valencia en un diagrama de nivel de energía es la brecha de energía\(E_g\). La brecha de energía del material utilizado para hacer una célula solar o fotodetector determina las propiedades del dispositivo. Los fotones con energía mayor que la brecha de energía tienen suficiente energía para formar pares electrón-agujero mientras que los fotones con menos energía no pueden.
Si se aplica un gradiente de temperatura a través de una unión pn, las cargas fluyen. Cuando se calienta un lado del dispositivo, las cargas se mueven más rápidamente y estas cargas energéticas se difunden hacia el lado más frío. Este efecto, denominado efecto termoeléctrico Seebeck, se discute en el Capítulo 8.