6.7: Problemas
- Page ID
- 81930
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)6.1. Clasificar los materiales desde la brecha de energía más pequeña hasta la mayor brecha de energía:
- Arseniuro de indio, INAs
- Arseniuro de aluminio, ALAS
- Arseniuro de galio, GaAs
6.2. El diagrama de nivel de energía para una unión pn de silicio se muestra en la siguiente figura. Parte del dispositivo está dopado con átomos de Ga, y parte del dispositivo está dopado con átomos As. Etiquete lo siguiente:
- La banda de valencia
- La banda de conducción
- La brecha energética
- La región de tipo n
- La región de tipo p
- La capa de agotamiento
- La parte del dispositivo dopada con Ga
- La parte del dispositivo dopada con As
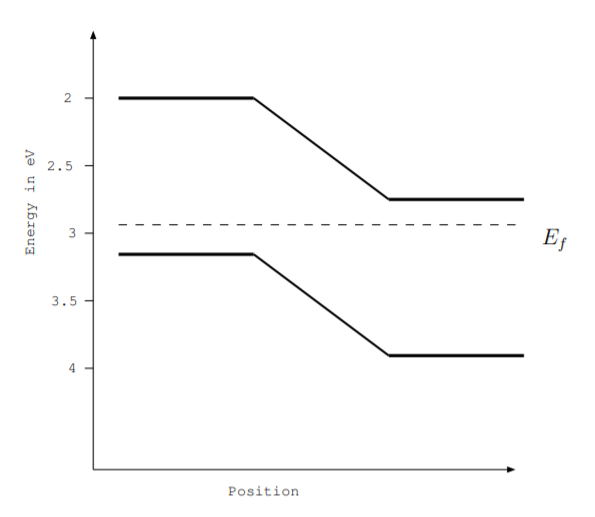
6.3. La figura del problema anterior muestra el diagrama de nivel de energía para una unión pn de semiconductores.
(a) Si esta unión pn se utiliza en un LED, ¿cuál será la longitud de onda en nm de la luz emitida por el LED?
b) Si esta unión pn se utiliza como célula solar, ¿qué rango de longitudes de onda de luz será absorbida por la célula solar?
6.4. Se utiliza un semiconductor para hacer un LED que emite luz roja a\(\lambda\) = 630 nm.
(a) Encontrar la brecha de energía en eV del semiconductor.
(b) Encontrar la energía en julios de un fotón emitido.
(c) Encontrar la energía en julios para Avogadro número constante de estos fotones.
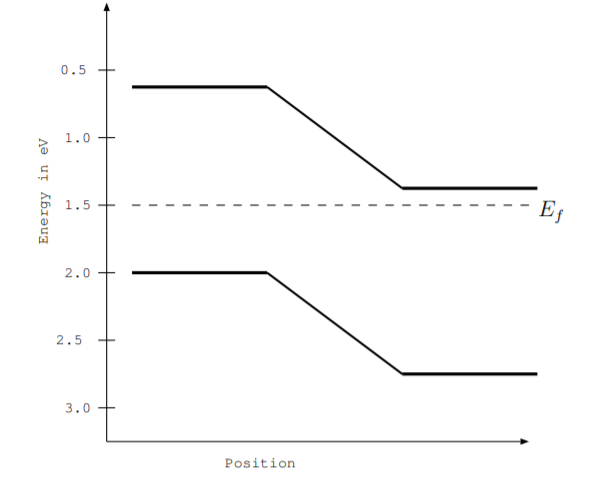
6.5. La siguiente figura muestra el diagrama de nivel de energía para un LED de arseniuro de galio.
(a) Encontrar la brecha energética.
(b) Encontrar la energía de un fotón emitido por el LED.
(c) Encontrar la frecuencia en Hz de un fotón emitido por el LED.
6.6. Utilice la Fig. 6.2.6 para responder a esta pregunta.
(a) Supongamos que le gustaría hacer un LED que emita luz roja con una longitud de onda de 650 nm. Sugerir tres posibles materiales semiconductores que podrían ser utilizados.
(b) Supongamos que le gustaría hacer una célula solar en capas utilizando capas de los siguientes materiales: InP,\(\text{In}_{0.5}\text{Ga}_{0.5}\text{As}\), y\(\text{AlAs}_{0.5}\text{Sb}_{0.5}\), ¿Qué capa estaría en la parte superior, en el medio, y en la parte inferior del dispositivo, y por qué?
6.7. Utilice la Fig. 6.2.6 para responder a esta pregunta.
(a) Encontrar la brecha energética de\(\text{InP}_{0.1}\text{As}_{0.9}\) en las unidades de julios.
(b) Si\(\text{InP}_{0.1}\text{As}_{0.9}\) se utiliza para hacer un LED, encuentre la frecuencia esperada, en Hz, de los fotones emitidos. c) ¿Sería mejor hacer una célula solar a partir de fosfuro de galio o fosfuro de indio? ¿Por qué?
6.8. Un panel solar produce una potencia promedio de 800 W. El panel se encuentra en una ubicación que recibe un promedio\(0.07 \frac{W}{cm^2}\) de energía óptica del sol. Supongamos que el panel tiene una eciencia del 9%.
(a) Calcular la superficie del panel solar en unidades\(m^2\).
b) Calcular la cantidad promedio de energía (en eV) producida en una semana.
6.9. Un panel solar tiene un área de\(50 m^2\), y produce un promedio de 4 kW de potencia. El panel se encuentra en una ubicación que recibe un promedio\(0.085 \frac{W}{cm^2}\) de energía óptica del sol. Calcular la eficiencia del panel.