7.5: Problemas

7.1. Identificar si los siguientes dispositivos operan en función de la emisión espontánea, la emisión estimulada o la absorción.

• Diodo emisor de luz
• Lámpara de descarga de gas
• Láser de iones de argón
• Panel solar
• Láser semiconductor

7.2. Considera un radiador de cuerpo negro a una temperatura de 6500 K. Usa Matlab, o software similar, para responder a esta pregunta.

(a) Encontrar la frecuencia que corresponde a la densidad de energía espectral máxima por unidad de ancho de banda.

(b) Encontrar la longitud de onda que corresponde a la densidad de energía espectral máxima por unidad de ancho de banda.

(c) Encontrar el valor de la densidad de energía espectral por unidad de ancho de banda\(\frac{J \cdot s}{m^3}\) en la frecuencia encontrada en parte\(a\).

7.3. Un láser semiconductor que emite luz\(\lambda = 500\) nm tiene una longitud de\(800 \mu m\). El ancho es\(12 \mu m\), y el grosor es\(5 \mu m\). ¿Cuántas longitudes de onda tiene el dispositivo en la dirección longitudinal? ¿Cuántas longitudes de onda tiene el dispositivo en cada dirección transversal?

7.4. Supongamos que un láser semiconductor tiene una longitud de\(800 \mu m\). La emisión láser puede ocurrir cuando la longitud de la cavidad es igual a un número entero de medias longitudes de onda. Qué longitudes de onda en el rango 650 nm\(< \lambda <\) 652 nm puede emitir este láser, y en cada caso, enumerar la longitud de la cavidad en longitudes de onda.

7.5. Supongamos que dos niveles de energía de un láser de gas están separados por 1.4 eV, y asumir que son igualmente degenerados (\(g_1 = g_2\)). La emisión espontánea coeciente de Einstein para las transiciones entre estos niveles de energía viene dada por\(A_{12} = 3 \cdot 10^6 s^{-1}\). Encuentra los otros dos coeficientes de Einstein,\(B_{12}\) y\(B_{21}\).

7.6. La brecha energética de las ALAs es de 2.3 eV, y la brecha de energía de AlSb es 1.7 eV [9, p. 19]. Las brechas energéticas de los materiales de composición Alas\(_x\) Sb\(_{1−x}\) con\(0 \leq x \leq 1\) varían aproximadamente linealmente entre estos valores [9, p. 19]. Supongamos que le gustaría hacer un láser semiconductor a partir de un material de composición Alas\(_x\) Sb\(_{1−x}\). Encontrar el valor de\(x\) que especifica la composición de un material que emite luz a longitud de onda\(\lambda = 640\) nm.

7.7. Los espectros láser a menudo son modelados por funciones lorentzianas. Una función lorentziana centrada en el origen con área bajo la curva de unidad tiene ecuación

\[y(x) = \frac{1}{\pi} \cdot \frac{0.5 \cdot \mathrm{FWHM}}{x^2 + (0.5 \cdot \mathrm{FWHM})^2}\nonumber \]

donde FWHM es el ancho completo a la mitad del máximo. El valor máximo de esta función es\(\frac{2}{\pi \cdot \mathrm{FWHM}}\). El espectro láser de la Fig. 7.7 está centrado cerca de\(\lambda = 570\) nm, tiene un FWHM de 5 nm y tiene una intensidad máxima de luminiscencia de 49. Encuentra una ecuación lorentziana que pueda modelar este espectro en particular.

7.8. Como se discutió en el problema anterior, los espectros láser a menudo son modelados por funciones lorentzianas. Para comprender mejor las funciones lorentzianas, use Matlab o software similar para este problema.

a) Trazar una función lorentziana centrada en el origen con FWHM 5 y amplitud máxima de unidad. En el mismo eje, traza una función gaussiana también centrada en el origen con FWHM 5 y amplitud máxima de unidad.

(b) Repita la parte a, pero ponga el eje vertical de sus parcelas en una escala logarítmica.

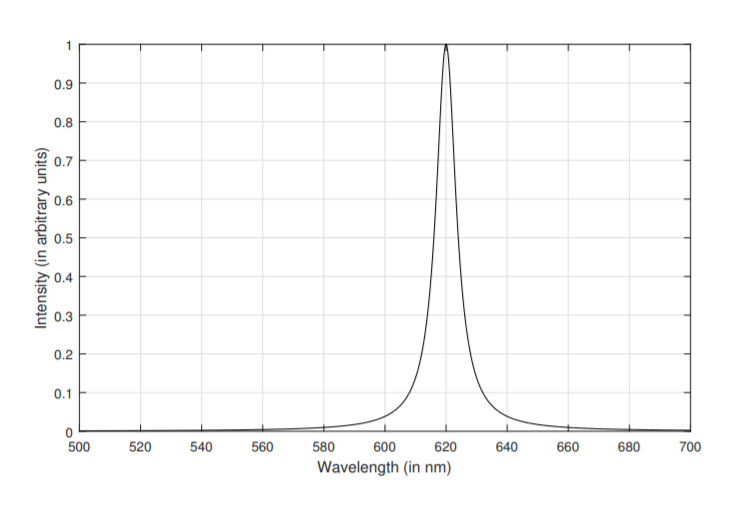
7.9. La figura ilustra un espectro láser. Aproximadamente encontrar:

(a) La longitud de onda de la intensidad máxima

b) El FWHM

c) El factor de calidad

7.10. Tres componentes principales de un láser son la bomba, el material activo y la cavidad. Cuatro tipos principales de láseres son los láseres de gas, los láseres semiconductores, los láseres de tinte y los láseres de estado sólido. Haga coincidir el componente de ejemplo con la mejor descripción del tipo de componente y tipo de láser en el que se encuentra especificado. (Cada respuesta se utilizará una vez.)

Componente de ejemplo
1. Bordes de un cristal de AlgaAs
2. Rhodamine 6G solución líquida
3. Espejo externo fabricado en vidrio SiO2 recubierto con aluminio
4. Batería de un puntero láser
5. Vidrio SiO2 dopado con 1% de átomos de Er
6. Gas CO2 en un tubo cerrado
7. Empalme Pn hecho de InGaAs
8. Láser de iones de argón utilizado para suministrar energía para excitar electrones de un Zafiro dopado con Ti

Descripción
A. Cavidad de un láser semiconductor
B. Cavidad de un láser de gas
C. Material activo de un láser semiconductor
D. Material activo de un láser de gas
E. Material activo de un láser de tinte
F. Material activo de un láser de estado sólido
G. Bomba de un láser semiconductor
H. Bomba de un láser de estado sólido

7.11. La intensidad de la luz solar en un día soleado es de alrededor\(0.1 \frac{W}{cm^2}\). La potencia del láser se puede confinar a un tamaño de punto muy pequeño. Supongamos que un láser produce un haz con tamaño de punto 1\(mm^2\). ¿Para qué potencia láser en vatios será equivalente la intensidad del haz a la intensidad de la luz solar en días soleados? Mirar al sol puede dañar un ojo, por lo que observar un rayo láser de esta intensidad es peligroso por la misma razón.