8.8: Problemas
- Page ID
- 81959
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)8.1. En un\(1 mm^3\) volumen, los\(10^{15}\) átomos de argón están a una temperatura de\(T = 300\) K. Calcular la presión del gas.
8.2. El gas argón está encerrado en un recipiente de un volumen fijo. A\(T = 300\) K, la presión del gas es de 50,000 Pa. A\(T = 350\) K, calcule la presión del gas.
8.3. Un globo se llena de átomos de helio a temperatura ambiente,\(72 ^{\circ}F\). Tiene un volumen de\(5 \cdot 10^{-5} m^3\), y el gas en el globo tiene una presión de\(10^6 \frac{N} {m^2}\). ¿Cuántos átomos de helio hay en el globo y cuál es la masa del gas?
8.4. Se utiliza un calentador resistivo para suministrar calor a una caja aislada. El calentador tiene corriente\(0.04 A\) y resistencia\(1 k\Omega\), y opera durante una hora. La energía se almacena en la caja o se usa para hacer girar un eje. Si la caja gana 2,500 J de energía en esa hora, ¿cuánta energía se utilizó para girar el eje?
8.5. Cualitativamente, explicar la diferencia entre cada par de cantidades relacionadas.
a) Efecto Seebeck y efecto Peltier
b) Conductividad térmica y conductividad eléctrica
8.6. Coincidir la descripción con la cantidad medida.
| A. Conductividad eléctrica |
| B. Coeficiente de Peltier |
| C. Coeficiente de Seebeck |
| D. Conductividad térmica |
| Coeficiente de E. Thomson |
| 1. Una barra está hecha de una unión de dos metales. Se coloca una corriente de 1 mA a través de la barra. La temperatura en cada extremo de la barra se mide en función del tiempo. La tasa de calor generado a través de la barra dividida por la corriente es ¿qué cantidad? |
| 2. Una barra está hecha de una unión de dos metales. Un extremo de la barra se mantiene a una temperatura de\(20 ^{\circ}C\) mientras que el otro se mantiene en\(45 ^{\circ}C\). El voltaje entre los extremos de la barra se mide con un voltímetro. Este voltaje dividido por\(15 ^{\circ}C\) es ¿qué cantidad? |
| 3. Un extremo de una barra de metal de se sostiene en\(45 ^{\circ}C\) mientras que el otro extremo se sostiene en\(20 ^{\circ}C\). Se coloca una corriente de 1 mA a través de la barra. Se mide la tasa de calor generado a través de la barra. El índice de calor generado dividido por el producto de 1 mA y ¿cuál\(1 ^{\circ}C\) es la cantidad? |
| 4. Un extremo de una barra de metal de área de sección transversal\(A\) se calienta a una temperatura de\(45 ^{\circ}C\). Se coloca un termopar a 3 cm por debajo de la barra alejada del calentador. El producto de la potencia disipada en el calentador tiempos 3 cm dividido por el producto de A y la diferencia de temperatura medida es ¿qué cantidad? |
| 5. Se introduce una corriente de 1 mA a través de una barra metálica de área de sección transversal\(A\). La caída de voltaje a través de la barra se mide con un voltímetro. La corriente multiplicada por la longitud de la barra dividida por el producto de la tensión medida y ¿qué cantidad\(A\) es? |
8.7. Explique cómo medir cada una de las siguientes cantidades, y enumere las herramientas necesarias para realizar la medición.
a) Conductividad eléctrica
b) Conductividad térmica
c) Coeficiente Peltier
8.8. Un dispositivo termoeléctrico tiene una figura de mérito de\(Z = 0.7 K^{-1}\). Un segundo dispositivo está hecho de los mismos materiales semiconductores, pero se ha dopado para que la conductividad eléctrica sea 20% mayor. Encuentra la figura de mérito del segundo dispositivo.
8.9. Un dispositivo termoeléctrico está hecho de un material con resistividad\(5 \cdot 10^{-8} \Omega \cdot m\) y coeficiente de Seebeck\(8.5 \cdot 10^{-5} \frac{V}{K}\). Se utilizó un cubo, de 1 cm en cada lado, para determinar la conductividad térmica. Un lado del cubo estaba calentado. En un estado estacionario, la tasa de transferencia de energía por conducción a través del cubo es de 1.8 W. La distribución de temperatura a través del material es lineal, y una diferencia de temperatura a través se mide para ser de 20 K a través del cubo. Encuentra la conductividad térmica\(\kappa\), y encuentra la figura de mérito\(Z\) para el material.
8.10. Como se muestra en la Fig. 8.5.2, un calentador suministra calor a un lado de una varilla de hierro. La varilla es cilíndrica con longitud 30 cm y radio 2 cm. El calentador suministra 2 W de potencia al borde de la varilla. El hierro tiene una conductividad térmica de\(\kappa = 80 \frac{W}{m \cdot K}\). Dos termopares están separados 15 cm como se muestra en la figura. ¿Cuál es la diferencia de temperatura (en grados Celsius) medida entre los dos termopares?
8.11. Un dispositivo termoeléctrico se utiliza para construir un refrigerador pequeño que puede contener dos latas pop. Cuando el dispositivo está funcionando, el lado frío del dispositivo está\(T = 10 ^{\circ}C\) mientras que el lado caliente del dispositivo, fuera del refrigerador, está en\(T = 42 ^{\circ}C\). ¿Cuál es la máxima eficiencia posible de este dispositivo?
8.12. El lado frío de un dispositivo termoeléctrico, utilizado para generar electricidad, está a una temperatura de\(100 ^{\circ}C\). ¿Cuál es la temperatura mínima del lado caliente del dispositivo necesaria para lograr una eficiencia de\(\eta_{ef\,f}\) = 15%?
8.13. La eficiencia de Carnot describe el límite de la eficiencia para algunos dispositivos. ¿Se aplica a los siguientes tipos de dispositivos? (Conteste sí o no.)
- Dispositivo de efecto Hall
- Láser de semiconductores
- Dispositivo fotovoltaico
- Dispositivo piezoeléctrico
- Dispositivo piroeléctrico
- Dispositivo termoeléctrico utilizado como sensor de temperatura
- Dispositivo termoeléctrico utilizado como refrigerador
- Dispositivo termoeléctrico utilizado para generar electricidad para un sistema de sensores
8.14. Las cifras muestran el coeficiente de Seebeck\($(T)\), la resistividad eléctrica\(\rho(T)\) =\(\frac{1} {\sigma(T)}\) y la conductividad térmica\(\kappa(T)\) trazados frente a la temperatura\(T\) para una familia de materiales conocidos como skutterudites. Estos materiales tienen la composición Tl\(_x\) Co\(_{4-y}\) Fe\(_y\) Sb\(_{12}\) y Tl\(_x\) Co\(_4\)\(_{12-y}\) Sb Sn\(_y\) donde\(x\) y\(y\) varían de cero a 1. Las cifras utilizadas con permiso de referencia [121]. Recientemente, los científicos han estado estudiando la posibilidad de fabricar dispositivos termoeléctricos a partir de estos materiales. Utilizando los datos de las cifras, aproximar la cifra termoeléctrica de mérito\(Z\) en unidades\(K^{-1}\) a una temperatura de\(T = 200\) K para el material con\(x = 0.1\).
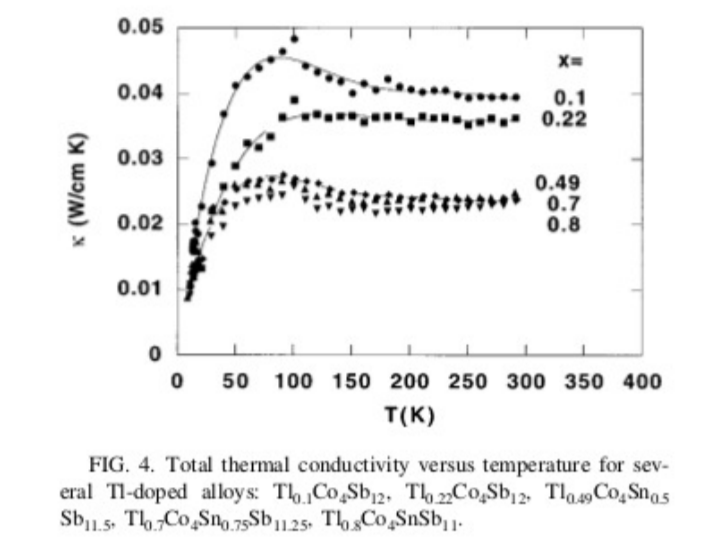
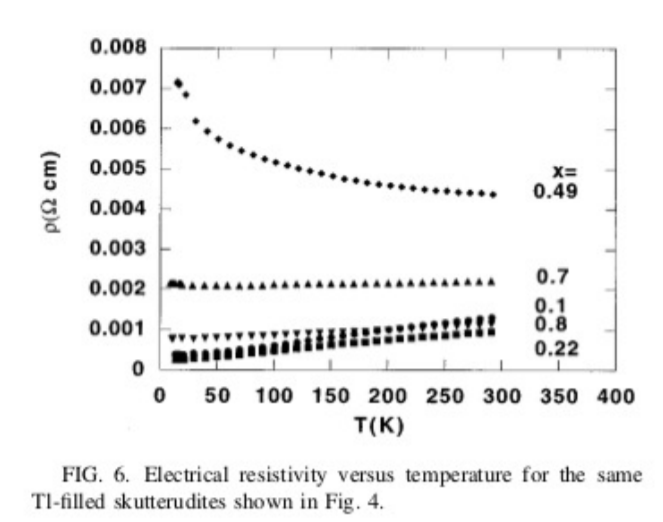
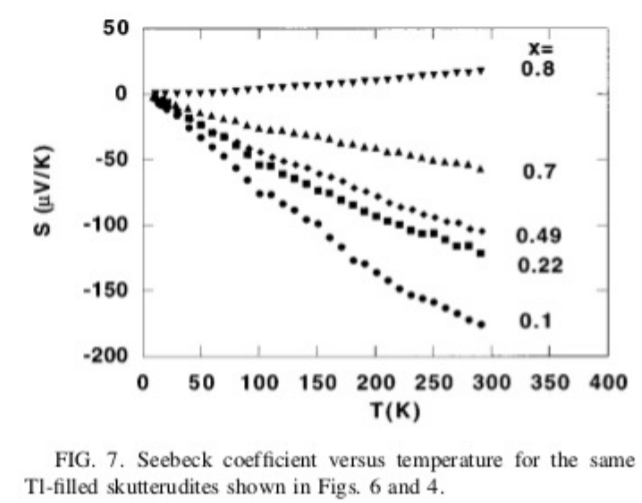
Figura\(\PageIndex{1}\)
8.15. Considere los datos en las cifras del problema anterior sobre el rango\(50 < T < 300\) K para el material con\(x = 0.1\). ¿A qué temperatura, dentro de este rango, se encuentra el producto de la figura de mérito por la temperatura\(ZT\), la mayor, y cuál es el valor correspondiente de\(ZT\)? Muestre su trabajo.
8.16. Las cifras muestran el coeficiente de Seebeck, la resistividad eléctrica y la conductividad térmica para tres materiales diferentes. Supongamos que nos gustaría utilizar estos materiales para construir dispositivos termoeléctricos que generen electricidad donde el lado frío del dispositivo está ligeramente por debajo de\(T \approx 400\) K, y el lado caliente está ligeramente por encima de\(T \approx 400\) K. Las cifras se utilizan con permiso de la referencia [122].
(a) Aproximadamente, calcular el coeficiente de Peltier y el coeficiente de Thomson para CeFe\(_4\) As\(_{12}\) near\(T \approx 400\) K.
(b) Supongamos que tiene un cubo de CeFe\(_4\) As\(_{12}\), 1 cm a cada lado. ¿Cuál es la resistencia R del cubo?
(c) Cuál es la cifra termoeléctrica de mérito\(Z\) para CeFe\(_4\) Como\(_{12}\) cerca de\(T \approx 400\) K. Incluya unidades en su respuesta.
d) Todo lo demás igual, cuál de los tres materiales produciría el mayor voltaje para una diferencia de temperatura dada. Justifica tu respuesta.
e) ¿Cuál de los tres materiales tiene la mayor figura termoeléctrica de mérito? Justifica tu respuesta.
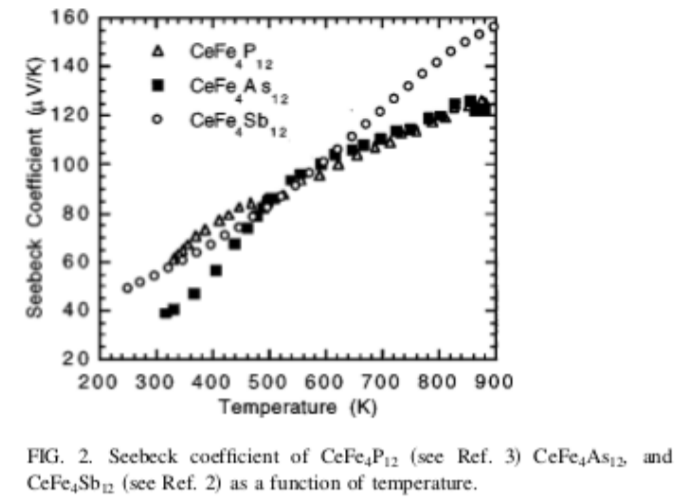
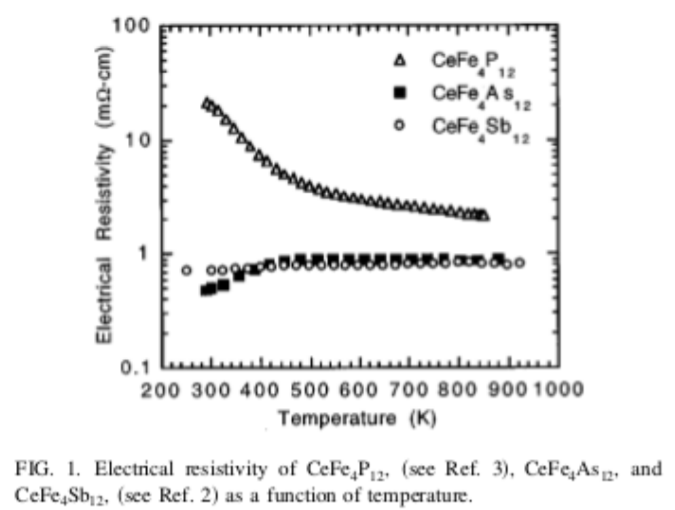
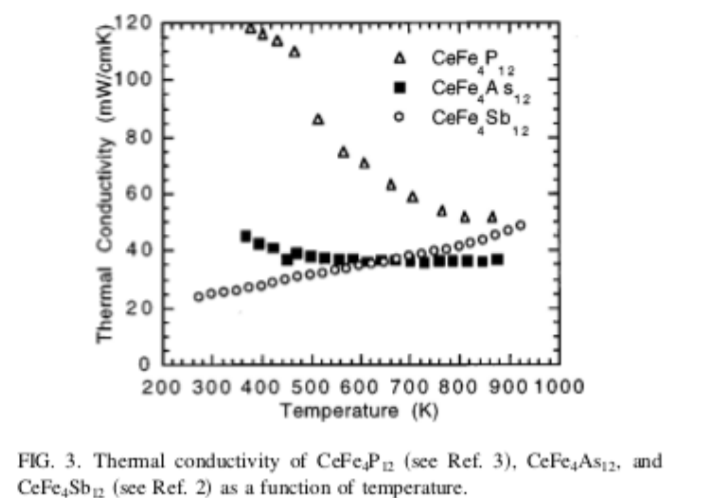
Figura\(\PageIndex{2}\)


