10.5: Electrofluídicos
- Page ID
- 81831
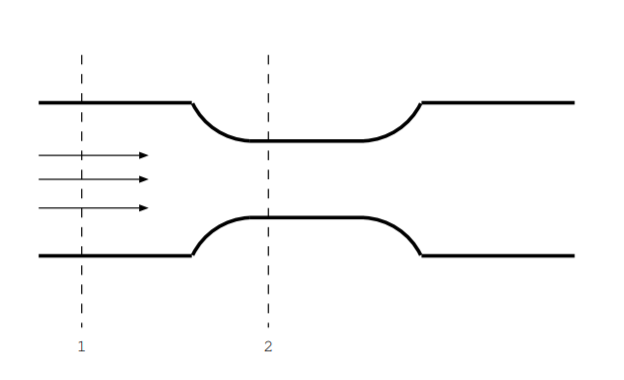
Los dispositivos electrohidrodinámicos (EHD) convierten entre energía eléctrica y flujo de fluido. Estos dispositivos también se conocen como dispositivos electrocinéticos. Los dispositivos microfluídicos son dispositivos EHD que están estampados en una sola oblea de silicio u otro sustrato, y las escalas de longitud suelen ser inferiores a un milímetro [159]. Los ingenieros han construido bombas EHD, válvulas, mezcladores, separadores y otros dispositivos EHD [159] [160]. Se han utilizado dispositivos electrohidrodinámicos o microfluídicos en productos que incluyen impresoras de chorro de tinta, detectores químicos, máquinas para secuenciación de ADN o análisis de proteínas, y bombas de insulina [61] [160] [161].
Algunos dispositivos EHD operan a partir de la idea de la ecuación de Bernoulli, y esta relación es una consecuencia directa de la conservación de energía. Para ilustrar la física fundamental de esta idea, comience por considerar un dispositivo más simple, una tubería constreñida. Esta tubería convierte la energía de un diferencial de presión a energía cinética [103, ch. 3] [162, p. 346]. Considera un fluido con viscosidad cero y conductividad térmica cero que fluye a través de una tubería horizontal (por lo que la gravedad puede ser ignorada). La figura\(\PageIndex{1}\) ilustra esta geometría. La velocidad\(\overrightarrow{v}\) y la presión\(\mathbb{P}\) son diferentes en ubicaciones con diferente diámetro de tubería, por ejemplo, las ubicaciones 1 y 2 en la figura. Considera una pequeña cantidad de agua con masa\(m = \rho_{dens} \Delta \mathbb{V}\) donde\(\rho_{dens}\) está la densidad y\(\Delta \mathbb{V}\) es el pequeño volumen. Supongamos que hay dos, y sólo dos, componentes de la energía: la energía cinética y la energía debida al fluido comprimido. Al pasar de la ubicación 1 a la ubicación 2, la presión de esta pequeña masa de fluido cambia. El cambio en la energía debido a la compresión de esta gota de agua es igual a\((\mathbb{P}_1 - \mathbb{P}_2) \Delta \mathbb{V}\). La energía cinética también cambia, y el cambio en la energía cinética viene dado por
\[\frac{1}{2} m|\overrightarrow{v_{1}}|^{2}-\frac{1}{2} m|\overrightarrow{v_{2}}|^{2}=\frac{1}{2}\left(\rho_{\text {dens}} \Delta \mathbb{V}\right)\left(|\overrightarrow{v_{1}}|^{2}-|\overrightarrow{v_{2}}|^{2}\right). \nonumber \]
Sin embargo, la energía se conserva, por lo que
\[\left(\mathbb{P}_{1}-\mathbb{P}_{2}\right) \Delta \mathbb{V}+\frac{1}{2}\left(\rho_{\text {dens}} \Delta \mathbb{V}\right)\left(|\overrightarrow{v_{1}}|^{2}-|\overrightarrow{v_{2}}|^{2}\right)=0. \nonumber \]
Esta expresión se puede simplificar algebraicamente.
\[\mathbb{P}_{1}-\mathbb{P}_{2}+\frac{1}{2} \rho_{\text {dens}}\left|\vec{v}_{1}\right|^{2}-\frac{1}{2} \rho_{\text {dens}}\left|\vec{v}_{2}\right|^{2}=0 \nonumber \]
\(\mathbb{P}\)Tanto la presión como la velocidad\(\overrightarrow{v}\) son funciones de ubicación. La única forma en que esta expresión puede ser cierta para todas las ubicaciones es si es verdadera para cada ubicación y una constante.
\[\mathbb{P}_{1}+\frac{1}{2} \rho_{\text {dens}}|\overrightarrow{v_{1}}|^{2}=\mathbb{P}_{2}+\frac{1}{2} \rho_{\text {dens}}|\overrightarrow{v_{2}}|^{2}=\text { constant } \nonumber \]
La ecuación de Bernoulli con los supuestos bastante severos anteriores se convierte
\[\mathbb{P}+\frac{1}{2} \rho_{\text {dens}}|\vec{v}|^{2}=\text { constant }. \label{10.5.5} \]
La ecuación de Bernoulli también se utiliza para describir la elevación de una lámina de aire o la trayectoria de una pelota curva en el béisbol [162, p. 350]. En algunos EHD la electricidad induce cambios en la presión o volumen de un canal microfluídico. El fluido en estos dispositivos puede ser conductor o aislante. Como se ve en la Ecuación\ ref {10.5.5}, este cambio en la presión induce un cambio en la velocidad del fluido.
En otros EHD, los voltajes aplicados ejercen fuerzas sobre los fluidos conductores. Un objeto cargado en un campo eléctrico externo\(\overrightarrow{E}\) siente una fuerza en la dirección del campo eléctrico. Una corriente en un campo magnético externo\(\overrightarrow{B}\) siente una fuerza. La dirección de esta fuerza es perpendicular tanto a la dirección de la corriente como a la dirección del campo magnético externo. Estos efectos son resumidos por la ecuación de fuerza de Lorentz
\[\overrightarrow{F} = Q \left( \overrightarrow{E} +\overrightarrow{v} \times \overrightarrow{B} \right) \nonumber \]
que se discutió en el Capítulo 5. En ese capítulo se discutieron los dispositivos de efecto Hall y los dispositivos magnetohidrodinámicos, los cuales se pueden entender mediante la ecuación de fuerza de Lorentz con un campo magnético externo pero sin campo eléctrico. Este tipo de EHD se puede entender por la ecuación de fuerza de Lorentz con un campo eléctrico externo pero sin campo magnético. El líquido en estos dispositivos debe ser conductor. Cuando se aplica una tensión a través de este tipo de EHD, se induce un campo eléctrico que hace que el líquido fluya, y se dice que este efecto se debe a un potencial de flujo [159]. Un efecto relacionado llamado electroforesis ocurre en líquidos que contienen partículas cargadas [161]. Si se aplica un campo eléctrico, estas partículas se moverán. Este efecto se ha demostrado con moléculas de ADN cargadas y moléculas de proteína cargadas en soluciones [161].
Otros dispositivos EHD operan cambiando la polarización del material de un líquido aislante, y este efecto se llama dielectroforesis. El concepto de polarización material se discutió en la Sección 2.2.1. Si aplicamos un campo eléctrico a través de un conductor, ya sea que ese conductor sea sólido o líquido, las cargas fluirán. Si aplicamos un campo eléctrico a través de un dieléctrico, el material puede polarizarse. En otras palabras, habrá algún desplazamiento de carga neta aunque todos los electrones permanezcan unidos a átomos. El campo eléctrico externo hace que tanto los átomos del líquido se polaricen como estos átomos polarizados fluyan.
Hay una serie de otros efectos de EHD interrelacionados. La electroósmosis puede ocurrir en fluidos con carga superficial. En algunos líquidos, los iones se forman en la superficie debido a enlaces químicos desapareados, debido a iones adsorbidos en la superficie, o por otras razones. Si se aplica un campo eléctrico a través de esta capa de cargas, el fluido fluirá, y este efecto se llama electroósmosis [161] [159]. Además, un campo eléctrico externo aplicado a través de un fluido puede calentar parte del fluido y causar un gradiente de temperatura. El fluido puede fluir debido al gradiente de temperatura, y este efecto se denomina flujo electrotérmico [161]. Otro efecto, conocido como electrohumectación, ocurre en los líquidos conductores. En la interfaz de un conductor sólido y un líquido conductor, se construyen cargas [61]. Nuevamente, si se aplica un campo eléctrico, el líquido fluirá.