11.4: Ejemplo de Muelle Masivo

Ejemplos en esta sección y en la siguiente sección ilustrarán cómo podemos usar la ecuación de Euler-Lagrange para encontrar la ecuación de movimiento que describe un proceso de conversión de energía. Considere un sistema compuesto por una masa y un resorte donde la energía se transfiere entre la energía potencial del resorte almacenada en el resorte comprimido y la energía cinética de la masa. La masa se especifica por\(m\) en kg. Se une a un resorte con resorte constante\(K\) adentro\(\frac{J}{m^2}\). La posición de la masa se especifica por\(x(t)\) donde\(x\) es la variable dependiente en metros y\(t\) es la variable independiente tiempo en segundos. Supongamos que esta masa y resorte están fijos en un plano nivelado o de alguna otra manera no influenciados por la gravedad. Este sistema de resorte de masa se ilustra en el lado izquierdo de la Fig. \(\PageIndex{1}\). Cuando el resorte se comprime, el sistema gana energía potencial de resorte. Cuando se libera el resorte, la energía se convierte de energía potencial de resorte a energía cinética. Supongamos que no se producen otros procesos de conversión de energía, como el calentamiento debido a la fricción.

Figura\(\PageIndex{1}\): Un sistema de muelles de masa.

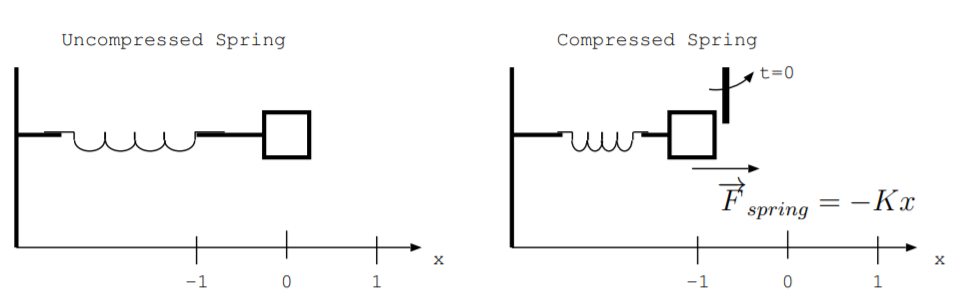
El lado derecho de la Fig. \(\PageIndex{1}\)muestra el resorte comprimido mantenido en su lugar por un sistema de retención. Porque\(t < 0\), el sistema no tiene energía cinética debido a que la masa no se mueve, y el sistema tiene energía potencial en el resorte comprimido. En este momento, la masa está en la posición\(x\) donde\(x < 0\). El resorte ejerce una fuerza sobre la masa,

\[\overrightarrow{F}_{spring}=-K x \hat{a}_{x} \nonumber \]

que está en la\(\hat{a}_{x}\) dirección.

At\(t = 0\), se elimina la restricción y la energía potencial de resorte se convierte en energía cinética. La primera forma es la energía potencial de resorte.

\[E_{potential\,energy} = \frac{1}{2}Kx^2 \nonumber \]

La segunda forma es la energía cinética de la masa.

\[E_{kinetic} = \frac{1}{2} m \left( \frac{dx}{dt} \right)^2 \nonumber \]

En cualquier instante del tiempo, cuando la masa está en el lugar\(x(t)\), la energía total es representada por el hamiltoniano.

\[H = E_{total} = E_{potential\,energy} + E_{kinetic} \nonumber \]

\[H=\frac{1}{2} K x^{2}+\frac{1}{2} m\left(\frac{d x}{d t}\right)^{2} \label{11.4.5} \]

El lagrangiano representa la diferencia entre las formas de energía.

\[\mathcal{L}=E_{potential\,energy} -E_{kinetic} \nonumber \]
\[\mathcal{L}\left(t, x, \frac{d x}{d t}\right)=\frac{1}{2} K x^{2}-\frac{1}{2} m\left(\frac{d x}{d t}\right)^{2} \nonumber \]

Tanto el hamiltoniano como el lagrangiano tienen unidades de julios. El potencial generalizado es

\[\frac{\partial \mathcal{L}}{\partial x} = Kx \nonumber \]

en unidades de newtons. Tenga en cuenta que\(Kx = − \overrightarrow{F}_{spring}\). El impulso generalizado es

\[\mathbb{M}=\frac{\partial \mathcal{L}}{\partial\left(\frac{d x}{d t}\right)}=-m \frac{d x}{d t} \nonumber \]

en unidades de las\(\frac{kg \cdot m}{s}\) cuales son las unidades de impulso.

En\(t = 0\), se quita la restricción. La masa sigue el camino\(x(t)\). Si conocemos al lagrangiano, podemos encontrar el camino por ensayo y error. Para encontrar el camino de esta manera, adivina un camino\(x(t)\) que sigue la masa y calcula la acción.

\[\mathbb{S}=\left|\int_{t_{1}}^{t_{2}} \frac{1}{2} m\left(\frac{d x}{d t}\right)^{2}-\frac{1}{2} K x^{2}\right| d t \label{11.4.10} \]

Adivina repetidamente otro camino y calcula la acción. El camino con la menor acción de todos los caminos posibles es el camino que sigue la masa. Este camino tiene la menor diferencia entre la energía potencial y la energía cinética integrada a lo largo del tiempo.

Podemos pensar en muchos caminos posibles, pero no físicos,\(x(t)\) que la masa puede seguir. La figura\(\PageIndex{2}\) ilustra dos rutas no físicas así como la ruta física derivada a continuación. Las rutas se consideran a lo largo del intervalo de tiempo\(0 < t < 1\). Los tres caminos suponen que inicialmente, en\(t = 0\), el resorte se comprime para que la masa esté en su ubicación\(x(0) = -1\). También, asumen que al final del intervalo, at\(t = 1\), el resorte se ha expandido para que la masa esté en su ubicación\(x(1) = 1\). Los posibles caminos ilustrados en la figura son

\[x_{1}(t)=2 t-1 \quad(\text { not physical })\nonumber \]

\[x_{2}(t)=2 t^{2}-1 \quad(\text { not physical })\nonumber \]

y

\[x_{3}(t)=-\cos (\pi t) \quad(\text { physical })\nonumber \]

Figura\(\PageIndex{2}\): Posibles caminos tomados por la masa y su acción correspondiente.

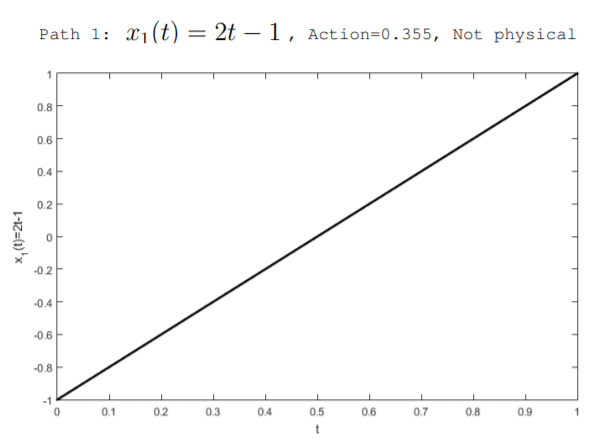
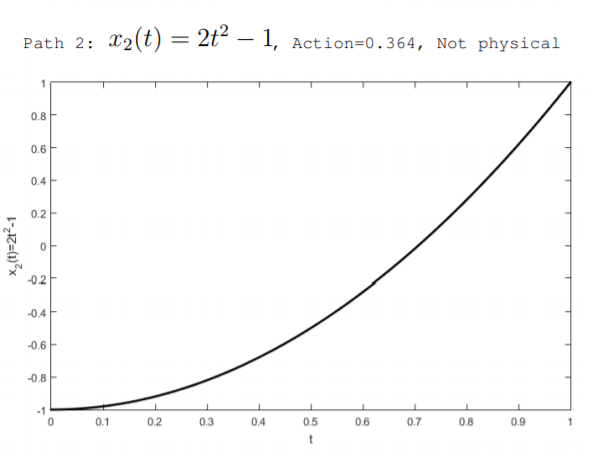
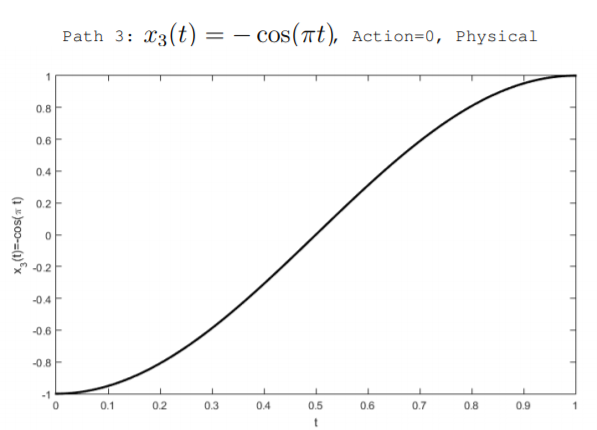
El camino\(x_1(t)\) describe un caso en el que la masa viaja a una velocidad constante. La trayectoria\(x_2(t)\) describe un caso en el que la masa acelera cuando se retira la restricción, y la trayectoria\(x_3(t)\) describe un caso en el que la masa primero acelera y luego se ralentiza. La acción de cada ruta se puede calcular usando la Ecuación\ ref {11.4.10}. Para fines de ejemplo, se\(K = \pi^2 \frac{J}{m^2}\) utilizan los valores de\(m = 1 kg\) y. El camino\(x_1(t)\) tiene\(\mathbb{S} = 0.355\), el camino\(x_2(t)\) tiene\(\mathbb{S} = 0.364\), y el camino físico\(x_3(t)\) tiene acción cero\(\mathbb{S} = 0\). Podemos derivar el camino que minimiza la acción y que se encuentra en la naturaleza usando la ecuación de Euler-Lagrange.

\[\frac{\partial \mathcal{L}}{\partial x}-\frac{d}{d t} \frac{\partial \mathcal{L}}{\partial\left(\frac{d x}{d t}\right)}=0 \nonumber \]

El primer término es el potencial generalizado. El segundo término es la derivada temporal del impulso generalizado. La ecuación del movimiento se encuentra juntando estas piezas.

\[Kx+m\frac{d^2x}{dt^2} = 0 \label{11.4.12} \]

El primer término de la ecuación del movimiento es\(- \left| \overrightarrow{F}_{spring} \right|\). El segundo término representa la aceleración de la masa. Acabamos de encontrar la ecuación del movimiento, y es una declaración de la segunda ley de Newton, la fuerza es la aceleración de masa por tiempos. También es una declaración de conservación de la fuerza sobre la masa.

La ecuación\ ref {11.4.12} es una ecuación diferencial lineal de segundo orden con coeficientes constantes. Es la famosa ecuación de onda, y su solución es bien conocida

\[x(t)=c_{0} \cos \left(\sqrt{\frac{K}{m}} t\right)+c_{1} \sin \left(\sqrt{\frac{K}{m}} t\right) \nonumber \]

donde\(c_0\) y\(c_1\) son constantes determinadas por las condiciones iniciales. Si sujetamos firmemente la masa al resorte, en lugar de dejar que la masa sea expulsada, oscilará como lo describe el camino\(x(t)\). La energía se conserva en este sistema. Para verificar la conservación de la energía, podemos demostrar que la energía total no varía con el tiempo. La energía total viene dada por el hamiltoniano de la Ecuación\ ref {11.4.5}. En este ejemplo, tanto el hamiltoniano como el lagrangiano no dependen explícitamente del tiempo,\(\frac{\partial H}{\partial t} =0\) y\(\frac{\partial \mathcal{L}}{\partial t} = 0\). En cambio, sólo dependen de los cambios en el tiempo. Por esta razón, decimos que tanto la energía total como la lagrangiana tienen simetría de traducción de tiempo, o decimos que son invariantes en el tiempo. La primavera y la masa se comportan igual hoy, una semana a partir de hoy, y un año a partir de hoy.

También podemos verificar la conservación de la energía algebraicamente demostrando eso\(\frac{dH}{dt} = 0\).

\[\frac{d H}{d t}=\frac{\partial H}{\partial t}+\frac{\partial H}{\partial x} \frac{d x}{d t}+\frac{\partial H}{\partial\left(\frac{d x}{d t}\right)} \frac{d^{2} x}{d t^{2}} \nonumber \]

\[\frac{d H}{d t}=0+K x \frac{d x}{d t}+m \frac{d x}{d t} \frac{d^{2} x}{d t^{2}} \nonumber \]

\[\frac{d H}{d t}=\frac{d x}{d t}\left(K x+m \frac{d^{2} x}{d t^{2}}\right)=0 \nonumber \]

Observe que la cantidad entre paréntesis en la línea anterior debe ser cero a partir de la ecuación de movimiento. La ecuación de Euler-Lagrange se puede dividir en un par de ecuaciones diferenciales de primer orden llamadas ecuaciones de Hamilton.

\[\frac{d \mathbb{M}}{d t} =-\frac{\partial H}{\partial x} \quad \text { and } \frac{d x}{d t} =\frac{\partial H}{\partial \mathbb{M}} \nonumber \]

Este ejemplo se resume en la Tabla\(\PageIndex{1}\). En analogía con el lenguaje utilizado para describir los circuitos y la electromagnetica, la relación entre la trayectoria generalizada y el potencial generalizado se conoce como la relación constitutiva. Siguiendo la Ecuación 11.1.6, la relación entre la trayectoria generalizada y el potencial generalizado es la capacidad generalizada, y en este ejemplo, es la inversa de la constante de resorte. Si bien\(x\) se supone que el desplazamiento es escalar, el vector\(\overrightarrow{x}\) se usa en la tabla para generalidad.

Cuadro\(\PageIndex{1}\): Resumen del sistema de resorte masivo en el lenguaje de cálculo de variaciones.

Dispositivo de almacenamiento de energía	Muelle lineal
Ruta Generalizada	Desplazamiento\(\overrightarrow{x}\) en m
Potencial Generalizado	\(\overrightarrow{F}\)Fuerza en\(\frac{J}{m} = N\)
Capacidad Generalizada	\(\frac{1}{K}\)en\(\frac{m^2}{J}\)
Relación constitutiva	\(\overrightarrow{x} = \frac{1}{K}\overrightarrow{F}\)
Energía	\(\frac{1}{2}\frac{1}{K}|\overrightarrow{x}|^2 = \frac{1}{2}K|\overrightarrow{F}|^2\)
Ley para el potencial	Segunda Ley de Newton\(\overrightarrow{F} = m\overrightarrow{a}\)