13.3: Derivación del Lagrangiano
- Page ID
- 81902
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)El propósito de este capítulo es encontrar el voltaje\(V (r)\) y la densidad de carga\(\rho_{ch}(r)\) alrededor de un átomo, y utilizaremos cálculo de variaciones para lograr esta tarea. Necesitamos hacer algunas suposiciones bastante severas para que este problema sea manejable. Considera un átomo neutro aislado con muchos electrones a su alrededor. Supongamos\(T \approx 0\) K, por lo que todos los electrones ocupan los niveles de energía más bajos posibles. Supongamos que el átomo es esféricamente simétrico. Todas las cantidades que encontramos, como voltaje, densidad de carga y Lagrangian, varían con\(r\) pero no varían con\(\theta\) o\(\phi\). Utilizaremos coordenadas esféricas con el origen en el núcleo del átomo. Si bien las cantidades varían con la posición, supongamos que ninguna cantidad varía con el tiempo. La densidad de carga nos\(\rho_{ch}(r)\) indica dónde es más probable que se encuentren los electrones en promedio. Se relaciona con la función de onda mecánica cuántica,\(\psi\), por
\[\rho_{c h}=-q \cdot|\psi|^{2} \nonumber \]
donde\(q\) está la magnitud de la carga de un electrón. Supongamos que todos los electrones que rodean al átomo están distribuidos uniformemente y pueden tratarse como si fueran una nube electrónica uniforme de alguna densidad de carga.
Escoge uno de los electrones del átomo, y considera lo que sucede cuando el electrón se mueve radialmente hacia dentro y hacia afuera. La figura\(\PageIndex{1}\) ilustra esta situación. A medida que el electrón se mueve, ocurre la conversión de energía El objetivo de esta sección es anotar lo hamiltoniano y lagrangiano para este proceso de conversión energética. Escribimos estas cantidades en las unidades de energía por unidad de volumen por electrón de valencia bajo consideración.
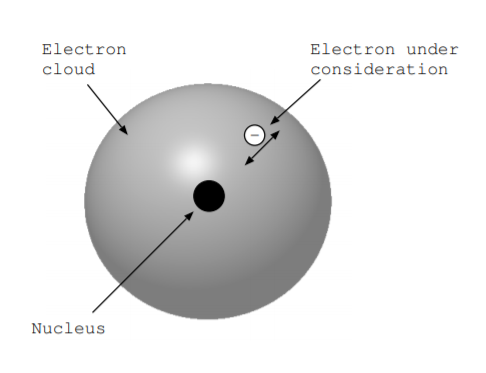
Para entender lo que sucede cuando se mueve el electrón, considera la energía del átomo con más detalle. La ley de Coulomb, introducida en la Ecuación 1.6.2, nos dice que los objetos cargados ejercen fuerzas sobre otros objetos cargados. Más específicamente, la intensidad del campo eléctrico\(\overrightarrow{E}\) debida a una carga puntual de\(Q\) culombios a una\(r\) distancia rodeada por un material con permitividad\(\epsilon\) viene dada por
\[\overrightarrow{E}=\frac{Q \hat{a}_{r}}{4 \pi \epsilon r^{2}}. \nonumber \]
El átomo está compuesto por protones cargados\(N\) positivamente. El electrón bajo consideración siente una fuerza de Coulomb atractiva debido a estos protones. Adicionalmente, el átomo tiene\(N\) electrones, y\(N - 1\) de estos ejercen una fuerza repulsiva de Coulomb sobre el electrón bajo consideración. Dado que existe una separación de carga y un campo eléctrico, se almacena la energía. Llamar al componente de la energía del átomo debido a la interacción Coulomb entre los protones del núcleo y el electrón bajo consideración\(E_{Coulomb\, e \,nucl}\). Llamar a la interacción de Coulomb entre el electrón bajo consideración y todos los demás electrones\(E_{e\, e \,interact}\). El átomo también tiene energía cinética. Llama a la energía cinética del núcleo\(E_{kinetic\, nucl}\) y a la energía cinética de todos los electrones\(E_{kinetic\, e}\). La energía del átomo es la suma de todos estos términos.
\[E_{atom} = E_{Coulomb\, e \,nucl.} + E_{kinetic\, nucl} + E_{e\, e \,interact} + E_{kinetic \,e} \nonumber \]
La energía debida al giro de los electrones y protones se ignora al igual que la energía debida a la interacción con cualquier otro objeto cargado cercano. A\(T \approx 0\) K, la energía cinética del núcleo será cercana a cero, por lo que podemos ignorar el término,\(E_{kinetic\, nucl} \approx 0\). La cantidad\(E_{kinetic\, e}\) no puede ser exactamente cero. En el capítulo 6 trazamos diagramas de nivel de energía para electrones alrededor de un átomo. Incluso en\(T = 0\) K, los electrones tienen algo de energía interna, y esta energía se denota por el nivel de energía ocupado.
Si tenemos un átomo grande con muchos electrones a su alrededor, la interacción Coulomb entre cualquier electrón y el núcleo está protegida por la interacción Coulomb de todos los demás electrones. Más específicamente, supongamos que tenemos un átomo aislado con\(N\) protones en el núcleo y\(N\) electrones a su alrededor. Si escogemos uno de los electrones,\(E_{Coulomb\, e \,nucl}\) para ese electrón se describe la energía almacenada en el campo eléctrico debido a la separación de carga entre el núcleo de carga positiva\(Nq\) y ese electrón. Sin embargo, también hay\(N - 1\) otros electrones que tienen una carga negativa. El término\(E_{e\, e \,interact}\) describe la energía almacenada en el campo eléctrico debido a la separación de carga entre los\(N - 1\) otros electrones y el electrón bajo consideración. Estos términos se cancelan un poco entre sí porque el electrón bajo consideración interactúa con\(N\) protones cada uno de carga positiva q y\(N - 1\) electrones cada uno de carga negativa\(-q\). No obstante, los términos no desaparecen por completo. Calculando
\[E_{Coulomb\, e \,nucl} + E_{e\, e \,interact} \nonumber \]
es complicado porque los electrones están en movimiento, y no sabemos realmente dónde están o incluso dónde es más probable que se encuentren. De hecho, estamos tratando de resolver por dónde es probable que se encuentren.
A medida que movemos el electrón bajo consideración hacia adentro y hacia afuera radialmente, la energía se transfiere entre (\(E_{Coulomb\, e \,nucl} + E_{e\, e \,interact}\)) y\(E_{kinetic\, e}\). El hamiltoniano es la suma de estas dos formas de energía por unidad de volumen, y el lagrangiano es la diferencia de estas dos formas de energía por unidad de volumen. Ambas cantidades tienen las unidades\(\frac{J}{m^3}\). Elija voltaje\(V (r)\) como ruta generalizada y densidad de carga\(\rho_{ch}(r)\) como potencial generalizado. La variable independiente de estas cantidades es la posición radial\(r\), no el tiempo. Ya podemos escribir el hamiltoniano y lagrangiano.
\[H\left(r, V, \frac{d V}{d r}\right) = \left(\frac{E_{Coulomb\, e \,nucl}}{\mathbb{V}} + \frac{E_{e\, e \,interact}}{\mathbb{V}}\right) + \frac{E_{kinetic\, e}}{\mathbb{V}} \nonumber \]
\[\mathcal{L} \left(r, V, \frac{d V}{d r}\right) = \left(\frac{E_{Coulomb\, e \,nucl}}{\mathbb{V}} + \frac{E_{e\, e \,interact}}{\mathbb{V}}\right) - \frac{E_{kinetic\, e}}{\mathbb{V}} \nonumber \]
El siguiente paso es escribir
\[\frac{E_{Coulomb\, e \,nucl}}{\mathbb{V}} + \frac{E_{e\, e \,interact}}{\mathbb{V}} \nonumber \]
en cuanto al camino\(V\). Como se detalla en la Tabla 12.2.3, la densidad de energía debida a un campo eléctrico\(\overrightarrow{E}\) viene dada por
\[\frac{E}{\mathbb{V}} = \frac{1}{2}\epsilon |\overrightarrow{E}|^2. \nonumber \]
Recuerda que\(E\) representa la energía mientras que\(\overrightarrow{E}\) representa el campo eléctrico. El campo eléctrico es el gradiente negativo de la tensión\(V (r)\).
\[\overrightarrow{E} = -\overrightarrow{\nabla}V. \nonumber \]
Podemos combinar estas expresiones y la Ecuación 13.2.6 para escribir el primer término del hamiltoniano y el lagrangiano en términos del camino generalizado.
\[\frac{E_{Coulomb\, e \,nucl}}{\mathbb{V}} + \frac{E_{e\, e \,interact}}{\mathbb{V}} = \frac{1}{2}\epsilon |\overrightarrow{\nabla}V|^2 \nonumber \]
\[H\left(r, V, \frac{d V}{d r}\right) = \left(\frac{1}{2}\epsilon |\overrightarrow{\nabla}V|^2\right) + \frac{E_{kinetic\, e}}{\mathbb{V}} \nonumber \]
\[\mathcal{L} \left(r, V, \frac{d V}{d r}\right) = \left(\frac{1}{2}\epsilon |\overrightarrow{\nabla}V|^2\right) - \frac{E_{kinetic\, e}}{\mathbb{V}} \nonumber \]
La siguiente tarea es describir el término restante\(\frac{E_{kinetic\, e}}{\mathbb{V}}\) como una función del camino generalizado también. Esta tarea es un poco más desafiante. Seguimos tomando el enfoque de hacer aproximaciones severas hasta que sea manejable. Tenemos que\(\rho_{ch}(r)\) expresarnos en función de\(V (r)\). Entonces con algo de álgebra, se\(\frac{E_{kinetic\, e}}{\mathbb{V}}\) puede escribir puramente en función de\(V (r)\).
Queremos generalizar sobre la energía cinética de los electrones. Sin embargo, cada electrón tiene su propia velocidad\(\overrightarrow{v}\) e impulso\(\overrightarrow{M}\). Estas cantidades dependen de la posición
\[\overrightarrow{r} = r \hat{a}_r + \theta \hat{a}_{\theta} + \phi \hat{a}_{\phi} \nonumber \]
de alguna manera desconocida. Además, el cálculo de\(\frac{E_{kinetic\, e}}{\mathbb{V}}\) depende de la densidad de carga\(\rho_{ch}(r)\), que es la cantidad desconocida que estamos tratando de encontrar. Tenemos más suerte al describir estas cantidades en el espacio recíproco, introducido en la Sec. 6.3. La posición se denota en el espacio recíproco por un vector de onda
\[\overrightarrow{k} = \tilde r \hat{a}_r + \tilde \theta \hat{a}_{\theta} + \tilde \phi \hat{a}_{\phi} \label{13.3.14} \]
Podemos describir las propiedades de un material describiendo cómo varían con la posición en el espacio real. Por ejemplo,\(\rho_{ch}(r)\) representa la densidad de carga de los electrones en función de la distancia r desde el centro del átomo. Nos puede interesar cómo otras cantidades, como la energía requerida para arrancar un electrón o la energía cinética interna a un electrón, varían también con la posición en el espacio real. En lugar de describir cómo varían las cantidades con la posición en el espacio real, podemos describir cómo varían las cantidades con la frecuencia espacial de los electrones. Esta es la idea detrás de representar cantidades en el espacio recíproco. Nos puede interesar cómo varía la densidad de carga de los electrones en función de la frecuencia espacial de las cargas en un cristal u otro material, y esta es la idea representada por funciones de vector de onda como\(\rho_{ch}(\overrightarrow{k})\). Estamos tratando de resolver por densidad de carga\(\rho_{ch}(r)\). Esperamos que los electrones sean más propensos a encontrarse a ciertas distancias\(r\) del centro del átomo que a otras distancias. Sin embargo, no hay patrón a la densidad de carga en función del vector de onda,\(\rho_{ch}(\overrightarrow{k})\). Supongamos que\(\rho_{ch}\) es aproximadamente constante con respecto a\(|\overrightarrow{k}|\) hasta algún nivel. Con algo más de trabajo, esta suposición nos permitirá resolver por densidad de carga\(\rho_{ch}(r)\).
La energía cinética de un solo electrón viene dada por
\[\frac{E_{kinetic\, e}}{e^-} = \frac{1}{2}m|\overrightarrow{v}|^2 \nonumber \]
donde\(m\) está la masa del electrón. Podemos escribir esta energía en términos de ímpetu,\(\overrightarrow{M} = m\overrightarrow{v}\). (Tenga en cuenta que el impulso\(\overrightarrow{M}\) y el impulso generalizado\(\mathbb{M}\) son diferentes y tienen diferentes unidades.)
\[\frac{E_{kinetic\, e}}{e^-} = \frac{|\overrightarrow{M}|^2}{2m} \nonumber \]
No sabemos cómo varía la energía en función de la posición r. En cambio, podemos escribir la energía en función del momento cristalino\(\overrightarrow{M}_{crystal}\) o del vector de onda\(\overrightarrow{k}\), y sabemos algo sobre la variación de estas cantidades. El impulso del cristal es igual al vector de onda escalado por la constante de Planck.
\[\overrightarrow{M}_{crystal} = \hbar \overrightarrow{k} \nonumber \]
Tiene las unidades de impulso\(\frac{kg \cdot m}{s}\), y se introdujo en la Sec. 6.3.2. La energía cinética de un electrón en función del momento cristalino viene dada por
\[\frac{E_{kinetic\, e}}{e^-} = \frac{\left(\overrightarrow{M}_{crystal}\right)^2}{2m} = \frac{\left(\hbar |\overrightarrow{k}|\right)^2}{2m}. \label{13.3.18} \]
Un vector en el espacio recíproco se representa Ecuación\ ref {13.3.14}, y la Ecuación\ ref {13.3.18} puede simplificarse porque estamos asumiendo simetría esférica\(\tilde \theta = \tilde \phi = 0\). La magnitud del vector de onda se convierte\(|\overrightarrow{k}| = \tilde r\), y podemos escribir la energía como
\[\frac{E_{kinetic\, e}}{e^-} = \frac{\hbar^2 \tilde r^2}{2m}. \label{13.3.19} \]
Así como cada electrón tiene su propio impulso\(m|\overrightarrow{v}|\), cada electrón tiene su propio impulso cristalino\(\hbar |\overrightarrow{k}|\). Sin embargo, conocemos alguna información sobre el vector\(|\overrightarrow{k}|\) de onda de los electrones en el átomo. A\(T = 0\) K, los electrones ocupan los estados de energía más bajos permitidos. Los estados energéticos están ocupados hasta algún estado ocupado más alto llamado la energía Fermi\(E_f\). Mientras que los ingenieros eléctricos usan el término energía Fermi, los químicos a veces usan el término potencial químico\(\mu_{chem}\). Los estados energéticos más bajos, están ocupados mientras que los superiores están vacíos. De manera similar, los vectores de onda están ocupados hasta algún vector de onda ocupado más alto llamado vector de onda Fermi\(k_f\).
\[ |\overrightarrow{k}| = \begin{cases} \text{filled state} & \tilde r < k_f \\ \text{empty state} & \tilde r > k_f \end{cases} \nonumber \]
La energía de Fermi y el vector de onda Fermi están relacionados por
\[E_f = \frac{\hbar^2 k^2_f}{2m}. \label{13.3.21} \]
Utilizamos la idea de espacio recíproco para escribir una expresión de la energía cinética de los electrones por unidad de volumen [136, p. 49]. La energía cinética debida a cualquier electrón en función de la posición en el espacio recíproco viene dada por la Ecuación\ ref {13.3.19}. Tenga en cuenta que a cada valor de\(|\overrightarrow{k}| = \tilde r\), el electrón tiene una energía cinética diferente. Para encontrar la energía cinética por unidad de volumen debida a todos los electrones, nos integramos sobre todo\(|\overrightarrow{k}| = \tilde r\) en coordenadas esféricas que están ocupadas por electrones, y luego dividimos por el volumen ocupado en el\(\overrightarrow{k}\) espacio.
\[\frac{E_{kinetic\, e}}{\mathbb{V}} = \frac{1}{\text{vol. occupied in } k \text{ space}} \cdot \int_{\text{filled } k \text{ levels}} \left(\frac{E_{kinetic\, e}}{e^-}\right)\left(\frac{e^-}{\text{volume}}\right) d (\text{vol. all } k \text{ space}) \nonumber \]
El número de electrones por unidad de volumen viene dado por
\[\left(\frac{e^-}{\text{volume}}\right) = \frac{-\rho_{ch}}{q}. \nonumber \]
El volumen ocupado en el espacio recíproco es\(\frac{4}{3}\pi k^3_f\), el volumen de una esfera de radio\(k_f\).
\[\frac{E_{kinetic\, e}}{\mathbb{V}} = \frac{1}{\frac{4}{3}\pi k^3_f} \cdot \int_{\text{filled } k \text{ levels}} \left(\frac{\hbar^2 \tilde r^2}{2m}\right)\left(\frac{-\rho_{ch}}{q}\right) d (\text{vol. all } k \text{ space}) \nonumber \]
Un elemento diferencial del volumen se expresa como
\[d^3 |\overrightarrow{k}| = \tilde r^2 \sin \tilde \theta\, d \tilde r \,d \tilde \theta \,d \tilde \phi. \nonumber \]
\[\frac{E_{kinetic\, e}}{\mathbb{V}} = \frac{1}{\frac{4}{3}\pi k^3_f} \cdot \int_{\text{filled } k \text{ levels}} \left(\frac{\hbar^2 |\overrightarrow{k}|^2}{2m}\right)\left(\frac{-\rho_{ch}}{q}\right) (\tilde r^2 \sin \tilde \theta\, d \tilde r \,d \tilde \theta \,d \tilde \phi) \nonumber \]
Como se describió anteriormente, los electrones ocupan estados en el espacio recíproco solo con\(0 \leq \tilde r \leq k_f\).
\[\frac{E_{kinetic\, e}}{\mathbb{V}} = \frac{1}{\frac{4}{3}\pi k^3_f} \cdot \int\limits_{\tilde r = 0}^{k_f} \,\int\limits_{\tilde \theta = 0}^{\pi} \,\int\limits_{\tilde \phi = 0}^{2\pi} \left(\frac{\hbar^2 \tilde r^2}{2m}\right)\left(\frac{-\rho_{ch}}{q}\right) (\tilde r^2 \sin \tilde \theta\, d \tilde r \,d \tilde \theta \,d \tilde \phi) \nonumber \]
La integral anterior puede ser evaluada directamente. El primer paso para evaluarlo es sacar constantes al exterior. Como se describió anteriormente,\(\rho_{ch}\) varía con\(r\) pero no\(\tilde r\), por lo que también se puede tirar fuera de la integral.
\[\frac{E_{kinetic\, e}}{\mathbb{V}} = \frac{-1}{\frac{4}{3}\pi k^3_f} \cdot \frac{\hbar^2 \rho_{ch}}{2mq} \int\limits_{\tilde r = 0}^{k_f} \,\int\limits_{\tilde \theta = 0}^{\pi} \,\int\limits_{\tilde \phi = 0}^{2\pi} \tilde r^4 \sin \tilde \theta\, d \tilde r \,d \tilde \theta \,d \tilde \phi \nonumber \]
La integral se separa y puede ser evaluada.
\[\frac{E_{kinetic\, e}}{\mathbb{V}} = \frac{-1}{\frac{4}{3}\pi k^3_f} \cdot \frac{\hbar^2 \rho_{ch}}{2mq} \left( \int\limits_{\tilde \theta = 0}^{\pi} \,\int\limits_{\tilde \phi = 0}^{2\pi} \sin \tilde \theta\, d \tilde r \,d \tilde \theta \,d \tilde \phi \right) \left( \int\limits_{\tilde r = 0}^{k_f} \tilde r^4 d \tilde r \right) \nonumber \]
\[\frac{E_{kinetic \, e}}{\mathbb{V}} = \frac{-1}{\frac{4}{3} \pi k^3_f} \cdot \frac{\hbar^2 \rho_{ch}}{2mq}4\pi \left(\frac{{k_f}^5}{5}\right) \nonumber \]
\[\frac{E_{kinetic \, e}}{\mathbb{V}} =\frac{-3 \rho_{ch} k^2_f \hbar^2}{10mq} \label{13.3.31} \]
La densidad de carga es una función de la posición en el espacio real\(r\), y estamos en el proceso de resolver para esta función,\(\rho_{ch}(r)\). Sin embargo, también depende de la energía de Fermi\(E_f\), y de ahí del vector de onda Fermi\(k_f\), para el átomo. A continuación, encontramos la relación entre\(\rho_{ch}\) y\(k_f\). Se permiten dos electrones por nivel de energía (spin up y spin down), de ahí por\(k\) estado lleno. El número de estados llenos por átomo en el espacio recíproco está relacionado con la densidad de carga.
\[\rho_{ch} = -2q \left( \frac{\text{no. filled } k \text{ states}}{\text{unit vol. in } k \text{ space}}\right) \nonumber \]
En la Sec. 6.3.1, vimos que una celda primitiva en el espacio recíproco era\((2 \pi )^3\) veces la celda primitiva en el espacio real, entonces
\[(\text{unit vol. } k \text{ space}) = (2 \pi )^3 \cdot (\text{unit vol. real space}) = (2 \pi )^3. \nonumber \]
Sabemos algo sobre los vectores de onda de estados rellenos en el espacio recíproco. A\(T = 0\) K, los estados más bajos se llenan, y todos los demás están vacíos, y se llenan hasta un radio de\(k_f\). El volumen de una esfera de radio\(k_f\) viene dado por\(\frac{4}{3}\pi k^3_f\), y esto representa el número de\(k\) estados llenos por volumen de espacio recíproco. Por lo tanto, podemos simplificar la expresión anterior.
\[\rho_{ch} = -2q \cdot \frac{4}{3} \pi k_f^3 \cdot \frac{1}{(2 \pi )^3} \nonumber \]
\[\rho_{ch} = \frac{-q}{3 \pi^2}k_f^3 \nonumber \]
\[k_f = \left(\frac{-3 \pi^2}{q}\rho_{ch}\right)^{1/3} \label{13.3.36} \]
Queremos escribir\(\frac{E_{kinetic\, e}}{\mathbb{V}}\) en función del camino generalizado\(V\). Ahora podemos lograr esta tarea combinando Ecuaciones\ ref {13.3.31} y\ ref {13.3.36}.
\[\frac{E_{kinetic \, e}}{\mathbb{V}}= \frac{-3\hbar^2}{10mq}\rho_{ch} \left(\frac{-3\pi^2}{q}\rho_{ch}\right)^{2/3} \nonumber \]
\[\frac{E_{kinetic \, e}}{\mathbb{V}}= \frac{-3\hbar^2}{10mq} \left(\frac{-3\pi^2}{q}\right)^{2/3} \rho_{ch}^{5/3} \nonumber \]
La energía eléctrica es producto de la carga y el voltaje. Más específicamente, a partir de la Ecuación 2.2.7, viene dada por
\[E = \frac{1}{2}QV. \nonumber \]
La densidad de energía eléctrica viene dada por
\[\frac{E}{\mathbb{V}} = \frac{1}{2}\rho_{ch}V. \label{13.3.40} \]
Utilice la ecuación\ ref {13.3.40} para relacionar\(\rho_{ch}\) y\(V\).
\[\frac{E_{kinetic \, e}}{\mathbb{V}}= \frac{1}{2}\rho_{ch}V =\frac{-3\hbar^2}{10mq} \left(\frac{-3\pi^2}{q}\right)^{2/3} \rho_{ch}^{5/3} \nonumber \]
Ahora hemos relacionado el camino generalizado y el potencial generalizado.
\[V = \frac{-3\hbar^2}{5mq} \left(\frac{-3\pi^2}{q}\right)^{2/3} \rho_{ch}^{2/3} \nonumber \]
\[\rho_{ch} = \left(\frac{-5mq}{3\hbar^2} \cdot \left(\frac{-3\pi^2}{q}\right)^{-2/3} \right)^{3/2} V^{3/2} \nonumber \]
\[\rho_{ch} = \left[ \left(\frac{-5mq}{3\hbar^2}\right)^{3/2} \left(\frac{-q}{3\pi^2}\right)\right] \cdot V^{3/2} \nonumber \]
Por último, podemos escribir\(\frac{E_{kinetic\, e}}{\mathbb{V}}\) en función de\(V\).
\[\frac{E_{kinetic \, e}}{\mathbb{V}}= \left[ \left(\frac{-5mq}{3\hbar^2}\right)^{3/2} \left(\frac{-q}{3\pi^2}\right)\right]V^{5/2} \nonumber \]
Observe que la cantidad entre paréntesis arriba es constante. El coeficiente\(c_0\) se define a partir del término entre paréntesis.
\[c_0 = \left(\frac{-5mq}{3\hbar^2}\right)^{3/2} \left(\frac{-q}{3\pi^2}\right) \label{13.3.46} \]
\[\frac{E_{kinetic \, e}}{\mathbb{V}}=c_{0} V^{5 / 2} \nonumber \]
Ahora podemos describir todos los términos del lagrangiano en términos de nuestro camino generalizado.
\[\frac{E_{Coulomb\, e \,nucl}}{\mathbb{V}} + \frac{E_{e\, e \,interact}}{\mathbb{V}} = \frac{1}{2}\epsilon |\overrightarrow{\nabla}V|^2 \nonumber \]
\[\frac{E_{kinetic \, e}}{\mathbb{V}} = c_{0} V^{5 / 2} \nonumber \]
El hamiltoniano representa la densidad total de energía, y el lagrangiano representa la diferencia de densidad energética de estas formas de energía. El hamiltoniano y lagrangiano tienen la forma\(H = H (r, V, \frac{dV}{dr})\) y\(\mathcal{L} = \mathcal{L} (r, V, \frac{dV}{dr})\) dónde\(r\) está la posición en coordenadas esféricas. No hay\(\theta\) o\(\phi\) dependencia de\(H\) o\(\mathcal{L}\). Todo es esféricamente simétrico.
\[H = \frac{1}{2}\epsilon |\overrightarrow{\nabla}V|^2 + c_{0} V^{5 / 2} \nonumber \]
\[\mathcal{L} = \frac{1}{2}\epsilon |\overrightarrow{\nabla}V|^2 - c_{0} V^{5 / 2} \nonumber \]
Como un aparte, consideremos una\(E_f = \mu_{chem}\) vez más la energía Fermi. Con algo de álgebra, podemos escribirlo en función del voltaje. Usa Ecuaciones\ ref {13.3.21},\ ref {13.3.36}, y\ ref {13.3.46}.
\[E_f= \frac{\hbar^2k^2_f}{2m} = \frac{\hbar^2}{2m} \left( \frac{-3\pi^2 \rho_{ch}}{q}\right)^{2/3} \nonumber \]
\[E_f= \frac{\hbar^2}{2m} \left( \frac{-3\pi^2}{q}\right)^{2/3} \left[ \left(\frac{-5mq}{3\hbar^2} \cdot \left( \frac{-3\pi^2}{q}\right)^{-2/3}\right)^{3/2} V^{3/2}\right]^{2/3} \nonumber \]
\[E_f = \frac{-5q}{6}V \nonumber \]
Observe que la energía Fermi es solo una versión escalada del voltaje\(V\) con respecto a un nivel del suelo en\(r = \infty\). Los ingenieros eléctricos suelen utilizar la palabra voltaje como sinónimo de potencial. Cuando los químicos usan el término potencial químico, se refieren a la misma cantidad simplemente escalada por una constante. Así como el voltaje es una cantidad fundamental de ingeniería eléctrica que representa lo difícil que es mover electrones, el potencial químico es una cantidad fundamental de química que representa lo difícil que es mover electrones alrededor.


