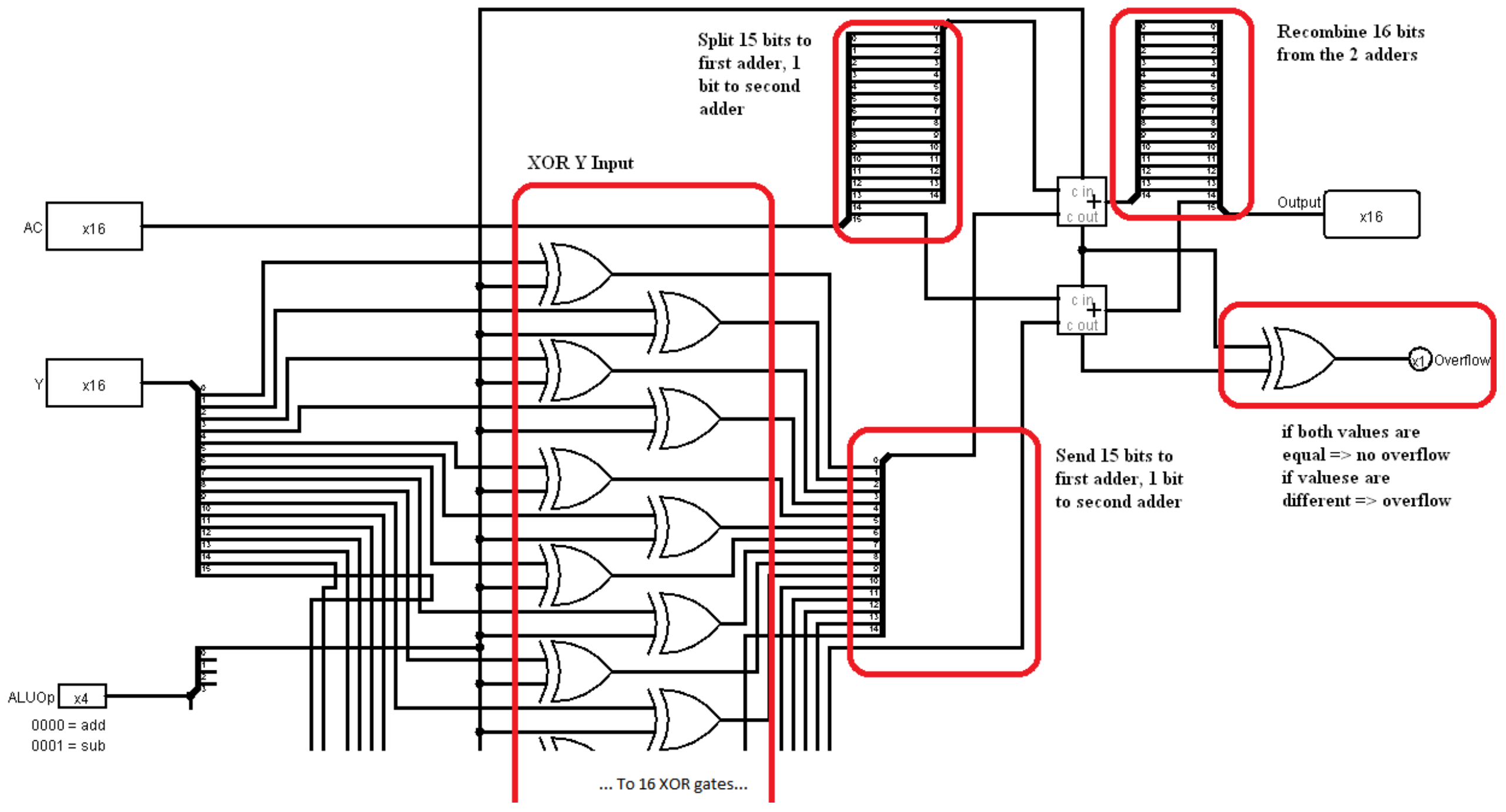
5.2: El ALU
( \newcommand{\kernel}{\mathrm{null}\,}\)
El ALU para esta unidad soporta suma y resta, y también implementa una bandera para indicar si la operación actual produjo un desbordamiento. Y el desbordamiento ocurre cuando se agregan dos números que son demasiado grandes para ser almacenados en los enteros de 16 bits implementados en la CPU. Por ejemplo, sumando 27000 + 25000 = 52000, un valor mayor que el entero máximo que se puede manejar, que es 32767. De igual manera -27000 + -25000 = -52000, un número que está demasiado por debajo del número entero mínimo que se puede manejar, que es -32768. Más adelante se discutirá cómo maneja la ALU estas situaciones.
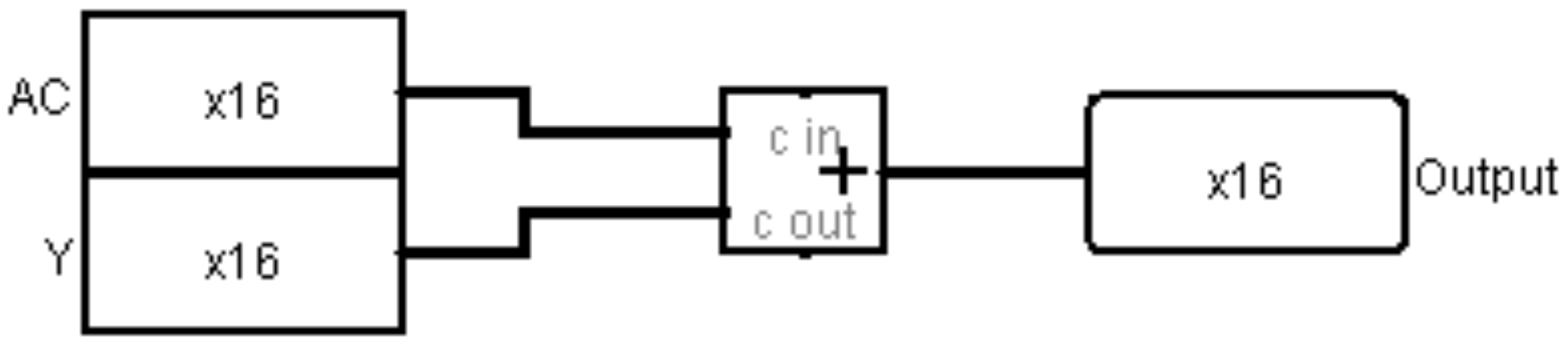
Una ALU simple que implementaría solo la adición de 16 bits es fácil de implementar, y se muestra en la siguiente figura. Dos valores de 16 bits ($ac e Y) se envían a la CPU, y se usa un sumador para agregar los valores y producir un resultado.
Para crear sustracción de implementos, se utiliza un poco de matemáticas creativas.
- Recuerde queX0=X; yX1=X'.
- Aritmética simple dice X + Y = X + (-Y)
- -Y = Y' + 1 (operación de negación complementaria de 2).
- La resta se puede implementar tomando cada bit de Y, XORIENDO con 1 (obteniendo el completamiento), luego sumando 1. Para sumar 1, pasa este bit al carry in de la sumadora.
- La adición se puede implementar tomando cada bit de Y, Xorándolo con 0 (para que no cambie) y sumando 0. Para sumar 0, pasa este bit al carry in del sumador.
- Por lo tanto, una unidad de Agregar/Restar puede implementarse pasando un bit indicador. Si el bit es 0, se realiza una operación de suma; si el bit es 1, se realiza una operación de resta.
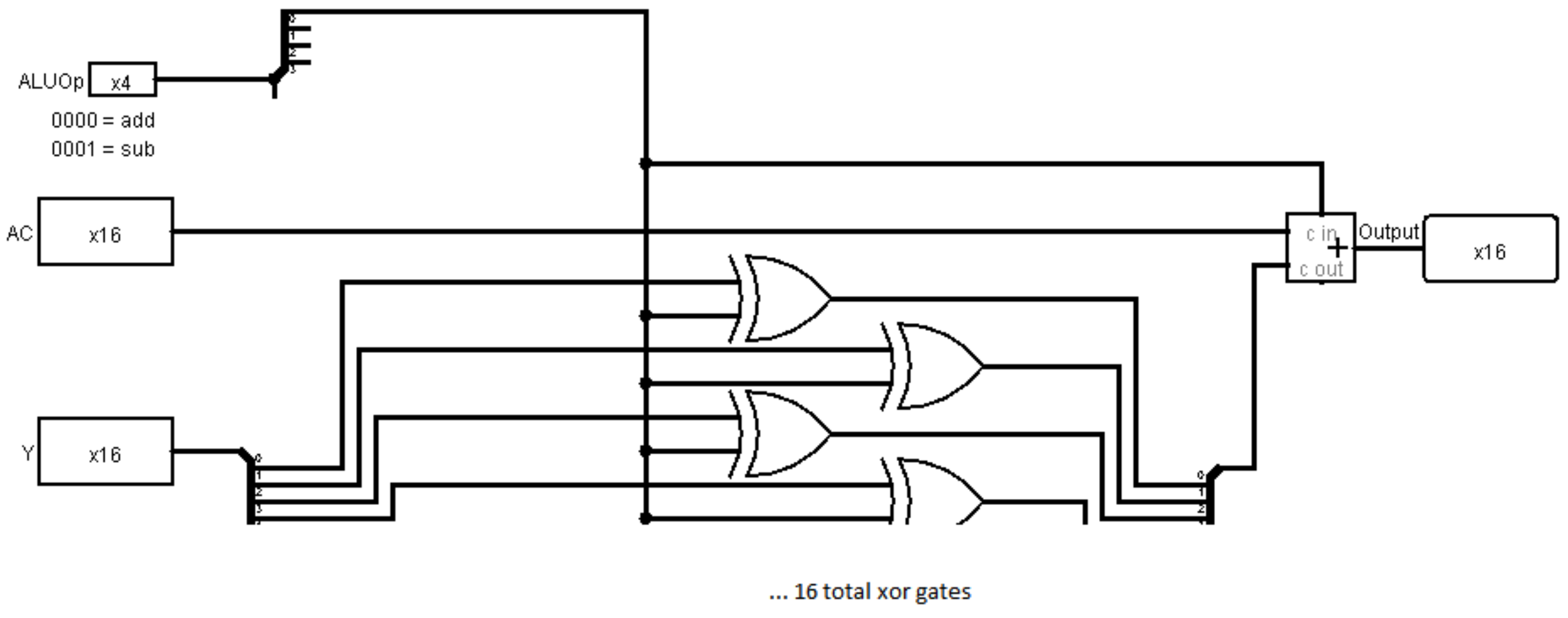
Este procedimiento se implementa en el siguiente circuito Logisim. Tenga en cuenta que todo lo que hace es XOR los bits Y con el valor de bandera 0/1, y luego agregar la bandera al sumador a través del acarreo en el sumador.
Hay una última adición por hacer a la ALU. Queremos verificar si hay un desbordamiento o no. La forma más fácil de hacer esto es verificar los bits para llevar y llevar hasta el último sumador completo. Si son iguales, no hay desbordamiento, pero si son diferentes, entonces se produjo desbordamiento. Estos dos bits se pueden verificar usando una puerta XOR. Si son iguales (sin desbordamiento), el XOR producirá 0, y si son diferentes (desbordamiento) el XOR producirá 1.