Saltar al contenido principal
LibreTexts Español

5.10: Detalle- Seguro de Vida

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    82111

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Un ejemplo de estadística y probabilidad en la vida cotidiana es su uso en seguros de vida. Consideramos aquí solo el seguro a plazo de un año (las compañías de seguros son muy creativas en la comercialización de pólizas más complejas que combinan aspectos de seguros, ahorros, inversión, ingresos de jubilación y minimización de impuestos).

    Al contratar una póliza de seguro de vida, pagas una prima de tantos dólares y, si mueres durante el año, a tus beneficiarios se les paga una cantidad mucho mayor. El seguro de vida puede pensarse de muchas maneras.

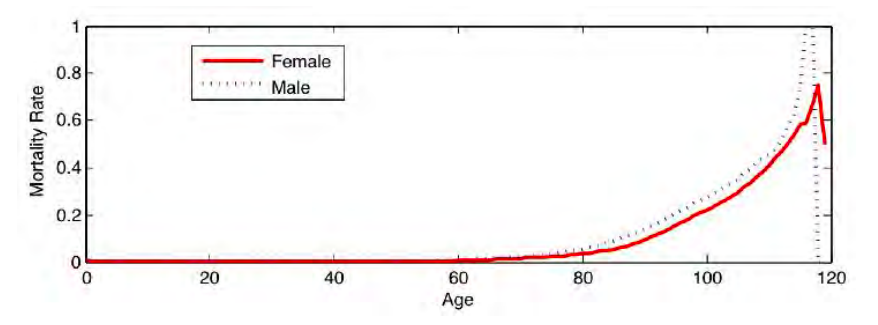
    Desde la perspectiva de un jugador, estás apostando a que morirás y la compañía de seguros está apostando a que vivirás. Cada uno de ustedes puede estimar la probabilidad de que muera, y debido a que las probabilidades son subjetivas, pueden diferir lo suficiente como para hacer que tal apuesta parezca favorable para ambas partes (por ejemplo, suponga que conoce una situación médica amenazante y no la revele a la aseguradora). Las compañías de seguros utilizan tablas de mortalidad como la Tabla 5.2 (que se muestra también en la Figura 5.4) para establecer sus tasas. (Curiosamente, las compañías de seguros también venden anualidades, que desde la perspectiva de un jugador son apuestas al revés, la compañía está apostando a que morirás pronto y estás apostando a que vivirás mucho tiempo).

    Otra forma de pensar sobre los seguros de vida es como inversión financiera. Dado que las compañías de seguros pagan en promedio menos de lo que cobran (de lo contrario irían a la quiebra), normalmente los inversionistas harían mejor invirtiendo su dinero de otra manera, por ejemplo poniéndolo en un banco.

    La mayoría de las personas que compran seguros de vida, por supuesto, no lo consideran ni como una apuesta ni una inversión, sino como una red de seguridad. Saben que si mueren, sus ingresos cesarán y quieren proporcionar un reemplazo parcial para sus dependientes, generalmente hijos y cónyuges. La prima es pequeña porque la probabilidad de muerte es baja durante los años en que dicha red de seguridad es importante, pero el beneficio en el improbable caso de muerte puede ser muy importante para los beneficiarios. Tal red de seguridad puede no ser tan importante para las personas muy ricas (que pueden permitirse la pérdida de ingresos), las personas solteras sin dependientes o las personas mayores cuyos hijos han crecido.

    La Figura 5.4 y la Tabla 5.2 muestran la probabilidad de muerte durante un año, en función de la edad, para la cohorte de residentes estadounidenses nacidos en 1988 (datos de The Berkeley Mortalidad Database\(^2\)).

    Screen Shot 2021-05-04 a las 10.00.17 PM.png
    Figura 5.4: Probabilidad de muerte durante un año para residentes estadounidenses nacidos en 1988.
    Edad Hembra Macho Edad Hembra Macho Edad Hembra Macho

    0

    		 0.008969 0.011126 40 0.000945 0.002205 80 0.035107 0.055995
    1 0.000727 0.000809 41 0.001007 0.002305 81 0.038323 0.061479
    2 0.000384 0.000526 42 0.00107 0.002395 82 0.041973 0.067728
    3 0.000323 0.000415 43 0.001144 0.002465 83 0.046087 0.074872
    4 0.000222 0.000304 44 0.001238 0.002524 84 0.050745 0.082817
    5 0.000212 0.000274 45 0.001343 0.002605 85 0.056048 0.091428
    6 0.000182 0.000253 46 0.001469 0.002709 86 0.062068 0.100533
    7 0.000162 0.000233 47 0.001616 0.002856 87 0.06888 0.110117
    8 0.000172 0.000213 48 0.001785 0.003047 88 0.076551 0.120177
    9 0.000152 0.000162 49 0.001975 0.003295 89 0.085096 0.130677
    10 0.000142 0.000132 50 0.002198 0.003566 90 0.094583 0.141746
    11 0.000142 0.000132 51 0.002454 0.003895 91 0.105042 0.153466
    12 0.000162 0.000203 52 0.002743 0.004239 92 0.116464 0.165847
    13 0.000202 0.000355 53 0.003055 0.00463 93 0.128961 0.179017
    14 0.000263 0.000559 54 0.003402 0.00505 94 0.142521 0.193042
    15 0.000324 0.000793 55 0.003795 0.005553 95 0.156269 0.207063
    16 0.000395 0.001007 56 0.004245 0.006132 96 0.169964 0.221088
    17 0.000426 0.001161 57 0.004701 0.006733 97 0.183378 0.234885
    18 0.000436 0.001254 58 0.005153 0.007357 98 0.196114 0.248308
    19 0.000426 0.001276 59 0.005644 0.008028 99 0.208034 0.261145
    20 0.000406 0.001288 60 0.006133 0.008728 100 0.220629 0.274626
    21 0.000386 0.00131 61 0.006706 0.009549 101 0.234167 0.289075
    22 0.000386 0.001312 62 0.007479 0.010629 102 0.248567 0.304011
    23 0.000396 0.001293 63 0.008491 0.012065 103 0.263996 0.319538
    24 0.000417 0.001274 64 0.009686 0.013769 104 0.280461 0.337802
    25 0.000447 0.001245 65 0.011028 0.015702 105 0.298313 0.354839
    26 0.000468 0.001226 66 0.012368 0.017649 106 0.317585 0.375342
    27 0.000488 0.001237 67 0.013559 0.019403 107 0.337284 0.395161
    28 0.000519 0.001301 68 0.014525 0.020813 108 0.359638 0.420732
    29 0.00055 0.001406 69 0.015363 0.022053 109 0.383459 0.439252
    30 0.000581 0.001532 70 0.016237 0.023393 110 0.408964 0.455882
    31 0.000612 0.001649 71 0.017299 0.025054 111 0.437768 0.47619
    32 0.000643 0.001735 72 0.018526 0.027029 112 0.466216 0.52
    33 0.000674 0.00179 73 0.019972 0.029387 113 0.494505 0.571429
    34 0.000705 0.001824 74 0.02163 0.032149 114 0.537037 0.625
    35 0.000747 0.001859 75 0.023551 0.035267 115 0.580645 0.75
    36 0.000788 0.001904 76 0.02564 0.038735 116 0.588235 1
    37 0.00083 0.001961 77 0.027809 0.042502 117 0.666667 1
    38 0.000861 0.002028 78 0.030011 0.046592 118 0.75 0
    39 0.000903 0.002105 79 0.032378 0.051093 119 0.5 0
    Cuadro 5.2: Tabla de mortalidad para residentes estadounidenses nacidos en 1988

    \(^2\)The Berkeley Mortality Database can be accessed online: http://www.demog.berkeley.edu/ bmd/states.html

    This page titled 5.10: Detalle- Seguro de Vida is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Paul Penfield, Jr. (MIT OpenCourseWare) via source content that was edited to the style and standards of the LibreTexts platform.