7.7: Procesos en cascada
- Page ID
- 82327
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Considera dos procesos en cascada. Este término se refiere a que la salida de un proceso sirva como entrada a otro proceso. Entonces los dos procesos en cascada pueden modelarse como un proceso más grande, si se ocultan los estados “internos”. Hemos visto que los procesos discretos sin memoria se caracterizan por valores de\(I\)\(J\),\(L\),\(N\), y\(M\). La Figura 7.10 (a) muestra un par de procesos en cascada, cada uno caracterizado por sus propios parámetros. Por supuesto, los parámetros del segundo proceso dependen de las probabilidades de entrada que encuentre, las cuales están determinadas por las probabilidades de transición (y probabilidades de entrada) del primer proceso.
Pero la cascada de los dos procesos es en sí misma un proceso discreto sin memoria y por lo tanto debe tener sus propios cinco parámetros, como se sugiere en la Figura 7.10 (b). Se pueden calcular los parámetros del modelo general
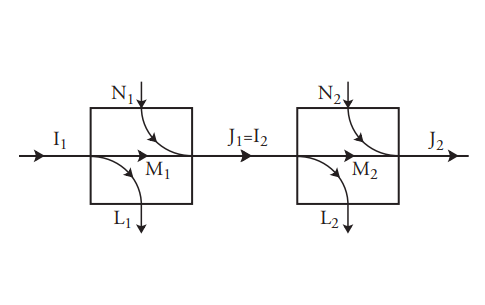
Figura 7.10: Cascada de dos procesos discretos sin memoria
ya sea de dos maneras. En primer lugar, las probabilidades de transición del proceso global se pueden encontrar a partir de las probabilidades de transición de los dos modelos que están conectados entre sí; de hecho, la matriz de probabilidades de transición es meramente el producto matricial de las dos matrices de probabilidad de transición para el proceso 1 y el proceso 2. Todos los parámetros se pueden calcular a partir de esta matriz y las probabilidades de entrada.
El otro enfoque es buscar fórmulas para\(I\),\(J\),\(L\)\(N\), y\(M\) del proceso general en términos de las cantidades correspondientes para los procesos componentes. Esto es trivial para las cantidades de entrada y salida:\(I = I_1\) y\(J = J_2\). Sin embargo, es más difícil para\(L\) y\(N\). Aunque\(L\) y generalmente\(N\) no se puede encontrar exactamente de\(L_1\)\(L_2\),\(N_2\),\(N_1\) y, es posible encontrar límites superior e inferior para ellos. Estos son útiles para proporcionar información sobre el funcionamiento de la cascada.
Se puede demostrar fácilmente que desde\(I = I_1\),\(J_1 = I_2\), y\(J = J_2\),
\(L − N = (L_1 + L_2) − (N_1 + N_2) \tag{7.33}\)
Entonces es sencillo (aunque quizás tedioso) demostrar que la pérdida\(L\) para el proceso general no siempre es igual a la suma de las pérdidas para los dos componentes\(L_1 + L_2\), sino que
\(0 ≤ L_1 ≤ L ≤ L_1 + L_2 \tag{7.34}\)
para que la pérdida quede delimitada desde arriba y abajo. También,
\(L_1 + L_2 − N_1 ≤ L ≤ L_1 + L_2 \tag{7.35}\)
de manera que si el primer proceso está libre de ruido entonces\(L\) es exactamente\(L_1 + L_2\).
Existen fórmulas similares para\(N\) en términos de\(N_1 + N_2\):
\(0 ≤ N_2 ≤ N ≤ N_1 + N_2 \tag{7.36}\)
\(N_1 + N_2 − L_2 ≤ N ≤ N_1 + N_2 \tag{7.37}\)
De estos resultados se derivan fórmulas similares para la información mutua de la cascada\(M\):
\(M_1 − L_2 ≤ M ≤ M_1 ≤ I \tag{7.38}\)
\(M_1 − L_2 ≤ M ≤ M_1 + N_1 − L_2 \tag{7.39}\)
\(M_2 − N_1 ≤ M ≤ M_2 ≤ J \tag{7.40}\)
\(M_2 − N_1 ≤ M ≤ M_2 + L_2 − N_1 \tag{7.41}\)
Otras fórmulas para\(M\) se derivan fácilmente de la Ecuación 7.19 aplicada al primer proceso y la cascada, y la Ecuación 7.24 aplicada al segundo proceso y la cascada:
\(\begin{align*} M &= M_1 + L_1 − L \\ &= M_1 + N_1 + N_2 − N − L_2 \\ &= M_2 + N_2 − N \\ &= M_2 + L_2 + L_1 − L − N_1 \tag{7.42} \end{align*}\)
donde la segunda fórmula en cada caso proviene del uso de la Ecuación 7.33. Tenga en cuenta que\(M\) no puede exceder cualquiera\(M_1\) o\(M_2\), es decir,\(M ≤ M_1\) y\(M ≤ M_2\). Esto es consistente con la interpretación de\(M\) como la información que pasa, la información que obtiene a través de la cascada debe ser capaz de obtener a través del primer proceso y también a través del segundo proceso.
Como caso especial, si el segundo proceso es sin pérdidas,\(L_2 = 0\) y luego\(M = M_1\). En ese caso, el segundo proceso no baja la información mutua por debajo de la del primer proceso. De igual manera si el primer proceso es sin ruido, entonces\(N_1 = 0\) y\(M = M_2\).
La capacidad\(C\) de canal de la cascada es, de manera similar, no mayor que la capacidad de canal del primer proceso o la del segundo proceso:\(C ≤ C_1\) y\(C ≤ C_2\). Otros resultados que relacionan las capacidades del canal no son una consecuencia trivial de las fórmulas anteriores porque\(C\) es por definición el máximo\(M\) sobre todas las distribuciones de probabilidad de entrada posibles; la distribución que maximiza\(M_1\) puede no conducir a la distribución de probabilidad para la entrada de el segundo proceso que maximiza\(M_2\).