Introducción

Del Autor

Existen numerosos libros de texto sobre aerodinámica y rendimiento de las aeronaves. Muchos de estos hacen trabajos maravillosos al partir de los conceptos básicos de la física y las matemáticas y derivar todas las importantes ecuaciones dinámicas de fluidos y dinámicas de vuelo que finalmente determinan la forma en que un avión vuela y se comporta. Estos, sin embargo, a menudo se escriben con tanto rigor matemático y científico que los estudiantes se pierden en las matemáticas y no logran apreciar la importancia física de los supuestos hechos a lo largo del camino y, por lo tanto, no entienden cómo usar los resultados. Otros textos buscan simplificar el rigor de las derivaciones y enfatizar solo las ecuaciones finales, incluso hasta el punto de insertar valores numéricos para muchas constantes en las ecuaciones hasta tal punto que solo funcionan cuando se usan con conjuntos predeterminados de suposiciones y unidades. Un resultado común es el mal uso de las ecuaciones por parte de los estudiantes en situaciones en las que los supuestos no son válidos o con conjuntos inapropiados de unidades. En este libro intentaré un enfoque diferente, discutiendo las bases físicas y matemáticas al tiempo que enfatizaré los supuestos hechos en el desarrollo de las relaciones que se presentan, pero lo haré sin detenerme en todos los pequeños pasos del camino. Se asumirá que el lector que quiera más rigor en el desarrollo de estas relaciones puede acudir a los muchos otros textos que hacen un trabajo muy admirable de presentar ese nivel de detalle.

El enunciado anterior no significa que voy a evitar todas las derivaciones de ecuaciones pero sí significa que no entraré en muchos detalles, especialmente donde las derivaciones pueden empantanarse en detalles matemáticos que tienen poco propósito más allá de atraer a los aficionados a las matemáticas.

Este libro buscará investigar los conceptos básicos tanto de la aerodinámica de los aviones como del rendimiento de los aviones. Si bien ocasionalmente veremos otras partes del régimen de vuelo, el énfasis estará en el vuelo subsónico y su flujo incompresible asociado. Examinaremos y enfatizaremos las limitaciones de mirar el vuelo de esta manera y discutiremos algunas de las consecuencias de aventurarnos más allá de estos límites en el régimen de flujo compresible, pero no analizaremos en detalle el vuelo y el rendimiento a velocidades más altas. También mantendremos nuestra discusión de muchos elementos importantes de la aerodinámica a un nivel muy básico, enfatizando los resultados generales más que los métodos detallados utilizados para obtener esos resultados. Hay muchos libros de texto finos en aerodinámica que están a disposición del lector que desee ir más allá del nivel de este libro y el estudiante de ingeniería aeronáutica o aeroespacial sin duda utilizará uno o más de esos textos en futuros cursos.

Las dos principales áreas de preocupación en este texto son la aerodinámica y el rendimiento. En general, la aerodinámica implica estudiar las relaciones de presión y velocidad de flujo a medida que el aire fluye alrededor de una forma aerodinámica como un avión o un ala. Si un flujo sobre un ala da una presión menor en la parte superior del ala que en la parte inferior, tenemos sustentación, y la aerodinámica busca explicar ese fenómeno y examinar cómo dar forma al ala en dos y tres dimensiones puede crear más sustentación de una manera más eficiente. Si las presiones en la parte delantera del avión o del ala son mayores que las de la parte posterior, obtenemos arrastre, y el aerodinamista quiere minimizar este arrastre al mismo tiempo que se maximiza el levantamiento. También es importante observar cómo se distribuyen esas presiones sobre el ala, ya que esa distribución puede influir en la probabilidad de que el flujo se separe del ala y provoque una mayor resistencia o pérdida del ala. La distribución de presión también puede determinar la naturaleza del flujo sobre el ala o avión justo en la superficie y esto influye en el tipo de arrastre que resulta de la fricción del aire que se mueve sobre la superficie. Estas fuerzas (levantar y arrastrar) son las fuerzas fundamentales que nos preocuparán cuando veamos el rendimiento del avión.

Las distribuciones de presión sobre el ala y otras partes de un avión también determinan la tendencia del avión a girar alrededor de su centro de gravedad (centro de masa) de manera que nos referimos como cabeceo (nariz arriba o abajo), balanceo (un ala hacia arriba, la otra hacia abajo) o guiñada (nariz izquierda o derecha). Estos tipos de movimiento son importantes para un tema completamente diferente, el de la dinámica del avión, la estabilidad y el control.

Un tercer tema para estudio posterior que se ve fuertemente afectado por estas fuerzas aerodinámicas sobre la aeronave y su ala son las estructuras. Obviamente, el avión debe estar diseñado para sostenerse unido bajo las tensiones provocadas por estas fuerzas. La estructura del avión debe ser lo más ligera posible al tiempo que le da la fuerza necesaria para resistir daños bajo la peor de las cargas aerodinámicas para las que se diseñó el avión. Y a veces olvidamos que el otro papel primordial de la estructura es dar la forma que se necesita para producir las fuerzas de presión y fricción deseadas.

Una cosa que intentaremos hacer mientras miramos la aerodinámica básica y el rendimiento es asegurarnos de que no miramos estos temas de forma aislada, sino que consideramos su impacto en la dinámica de las aeronaves y el diseño estructural. Por ejemplo, encontraremos que un cierto tipo de distribución de las fuerzas de sustentación aerodinámica a lo largo de la envergadura del ala de una punta a la otra producirá una carga “ideal” o “mínima resistencia”. Sin embargo, esta carga aerodinámica ideal no es la carga estructural ideal, y en el diseño de un avión real, ambas necesidades deben ser consideradas. También encontraremos que una “relación de aspecto” alta, o una gran relación de envergadura del ala para un área de ala dada, dará tanto un mejor rendimiento aerodinámico como un mejor rendimiento del avión que un ala con una “relación de aspecto” baja. Por otro lado, el ala que es mejor para la elevación y el arrastre y el rendimiento general del avión puede no ser muy bueno para un rendimiento dinámico óptimo de la aeronave en cosas como las maniobras de balanceo.

Otras dos cosas muy importantes que se enfatizarán en este texto serán una rigurosa atención a las unidades y la necesidad de controles continuos de la realidad para asegurarnos de que estamos obteniendo resultados que están “en el estadio de béisbol”; es decir, que tengan sentido en el mundo real. Con demasiada frecuencia, es la falta de atención a estas dos materias lo que causa más aflicción a los estudiantes al obtener las “respuestas correctas” en las pruebas y en la tarea, y fue la falta de atención a una de estas materias lo que resultó en una misión espacial muy cara a Marte que le faltaba todo el planeta hace un par de años.

Muchos libros de texto de ingeniería simplemente asumen que todo el trabajo siempre se realizará en un sistema unitario particular (generalmente SI) y que las ecuaciones desarrolladas incluyen constantes apropiadas al sistema elegido y ninguna otra. No vamos a hacer eso. Todas las ecuaciones en este texto serán completamente genéricas con respecto a las unidades, sin suposiciones sobre el uso de SI o inglés (americano) o cualquier otro sistema de unidades. Esto pretende obligar al alumno a llevar unidades apropiadas con cada número y resolver esas unidades según sea necesario para la solución de la ecuación. Esto debería, de hecho, ser útil para asegurar que la “respuesta” al cálculo es correcta ya que, si las unidades salen mal, es un indicio bastante bueno de que los números también están equivocados.

Este enfoque indudablemente molestará a los ávidos defensores de un sistema de unidades de otro, a aquellas personas que creen que solo un sistema de unidades es “políticamente correcto” y siempre debe ser utilizado aunque sus usuarios no tengan absolutamente ninguna idea del significado o los valores de las unidades utilizadas. Creo que es, sin embargo, importante contar con ecuaciones que obliguen al usuario a tener cuidado de resolver tanto números como unidades por dos razones. En primer lugar, resolver las unidades en las ecuaciones es, como se mencionó anteriormente, una manera bastante fácil e importante de asegurarse de que la “respuesta” es, en efecto, correcta. Segundo, independientemente de lo ideal que sería nuestro mundo si todos usaran el mismo sistema de unidades para todo lo que hacen, ese no es el caso, y es mi experiencia después de trabajar con profesores de ingeniería y estudiantes en Europa y Asia que pocas personas realmente tienen una buena sensación física para muchas de las unidades básicas del SI. Los ingenieros franceses me han preguntado qué es un Pascal, y muchos no logran entender que el Newton es una unidad de peso adecuada porque gran parte del mundo prefiere ignorar los efectos de la gravedad y trabajar solo con masa. Hasta que encuentre a un puñado de personas en cualquier parte del mundo que puedan decirme su peso en Newtons, sin hacer conversiones mentales a partir de libras (en Estados Unidos) o “piedras” (en Inglaterra) o convertir a partir de kilogramos de masa, no me convenceré de que solo podamos suponer que el uso de unidades SI en los libros de texto elimina los problemas de la unidad.

Esto también se relaciona con la importante idea de obtener una apreciación por las magnitudes adecuadas de las propiedades que estudiaremos en este texto. Siempre me sorprende cuando un estudiante está perfectamente feliz girando en un papel en el que ella o él ha calculado que un solo motor, avión impulsado por hélice está navegando en Mach 2! Parecería evidente que la respuesta es muy equivocada. En realidad, el estudiante probablemente ha hecho un cálculo sin prestar atención a las unidades y ha llegado a una respuesta de algo así como 2000 pies por segundo y no se ha molestado en pensar que esto es aproximadamente el doble de la velocidad del sonido. Quizás si la respuesta se hubiera calculado en millas por hora, la magnitud del valor habría causado una mayor impresión y habría provocado una alarma mental. Por otro lado, ¿se había encontrado la respuesta como 600 metros (metros?) por segundo, la mayoría de los estudiantes estadounidenses no tendrían idea de lo rápido que es esto realmente. Incluso en Gran Bretaña, donde las velocidades de las carreteras todavía se registran en millas por hora, los estudiantes pueden no haber reconocido de inmediato que esta respuesta violó una suposición de flujo incompresible. Entonces, así como sospecharíamos que nos habían engañado si pisamos una báscula operada con monedas y nos dijeran que pesábamos 2500 libras porque tenemos una sensación física para el rango adecuado de pesos humanos, necesitamos desarrollar un sentido de respuestas de “estadio de béisbol” para fuerzas aerodinámicas, velocidades, rangos de aviones y resistencia y parámetros similares que encontraremos en este texto.

El objetivo de este texto es proporcionar una cobertura “independiente” del rendimiento básico, subsónico, de la aeronave precedida de una introducción a los fundamentos de la aerodinámica que proporcionará un fondo suficiente para la comprensión de los temas a estudiar en el desempeño de las aeronaves. Los cálculos de rendimiento de la aeronave son esencialmente el resultado de simplemente equilibrar las fuerzas en un avión, levantar contra peso y empuje contra arrastre, y observar cómo estas balanzas funcionan juntas y cómo se ven afectadas por cosas como la velocidad y la altitud. Para entender este equilibrio debemos saber algo sobre estas fuerzas aerodinámicas que llamamos lift and drag y entender algo sobre cómo varían con la velocidad y la altitud. Este será nuestro objetivo en los tres primeros capítulos, conocer la aerodinámica y conocer cómo cambian las propiedades de la atmósfera con la altitud. También intentaremos tener alguna idea de cómo el piloto ve su entorno operativo utilizando la instrumentación disponible en la cabina y cómo eso podría relacionarse con el rendimiento y operación del avión.

Una vez que hayamos mirado alguna aerodinámica comenzaremos a usar nuestros conocimientos para explorar la forma en que funciona un avión. ¿Qué tan rápido o lento puede volar? ¿Qué tan alto puede subir y cuál es la tasa de ascenso? ¿Hasta dónde puede deslizarse? ¿Hasta dónde puede volar en un tanque de combustible? Todo esto se puede determinar simplemente equilibrando las fuerzas. Luego veremos un par de casos en los que debemos considerar la aceleración. Estos son despegue/aterrizaje y giro.

Por último, echaremos un vistazo a cómo tratar de equilibrar todas las cosas que hemos aprendido sobre el rendimiento para diseñar un avión que haga todo lo que queramos; es decir, despegar y aterrizar en la distancia deseada y también subir a la velocidad deseada, crucero a la velocidad objetivo, etc.

Problemas con la tarea

Los problemas de tarea al final de cada capítulo se basan en los ejemplos del texto para aportar experiencia en el trabajo con los materiales y métodos teóricos presentados en el texto. Muchos de los problemas piden el trazado de gráficas y se proporciona papel cuadriculado para ese propósito. La primera pregunta que muchos alumnos harán es: “¿Tengo que usar el papel cuadriculado? ¿No puedo trazarlos usando Excel o algún otro paquete de computadora?”

Es mi sensación de que hay valor en aprender a trazar a mano y, al usar estos ejes predimensionados de parcela, al alumno se le muestra algún límite en el alcance de la solución; es decir, si su gráfica no se ajusta a la escala proporcionada, ¡está mal! Trazar los datos a mano ofrece la “oportunidad” para que la persona que realiza el trazado piense un poco sobre los puntos que se trazan y determine si tienen sentido físicamente. Muchos cálculos de rendimiento de aeronaves están relacionados con el vuelo “dentro del sobre” donde el “sobre” es literalmente el área dentro de la curva en una trama y la visualización de tal envolvente puede ayudar a uno a entender lo que está sucediendo. Es mi experiencia que por alguna razón quienes tienen su computadora hacen la trama son mucho más propensos a estar perfectamente contentos con resultados que no tienen ningún sentido (¡ese Mach 3 Cessna 152!) que son los que trazan los resultados a mano, quizás simplemente porque el trazado manual de los resultados obliga a uno a tomarse el tiempo para mirar esos resultados y no asumir que son correctos solo porque fueron generados por un programa de computadora.

Al trazar datos los puntos de datos reales que se calculan (u obtienen del experimento) deben mostrarse con un pequeño símbolo como un cuadrado o un círculo o un triángulo. La curva general debe ir recorrida a través de esos puntos siguiendo una curva o trayectoria suave y no como un juego de conectar los puntos como las computadoras son propensas a hacer.

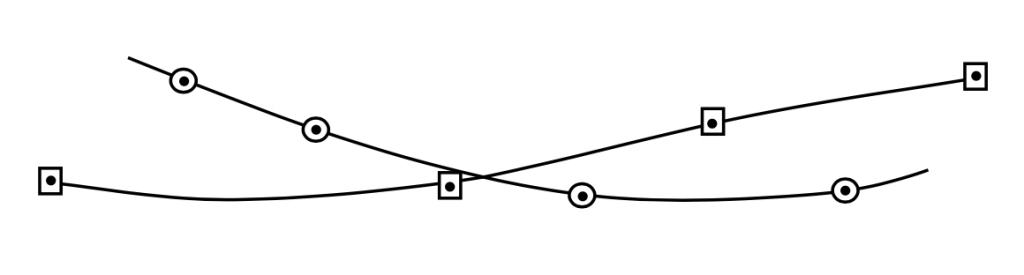
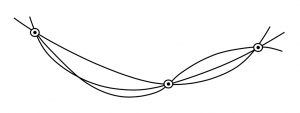
También hay que recordar que es necesario un número mínimo de puntos para definir una curva. Dos puntos de datos no dicen nada sobre las tendencias y tres puntos son marginales. El alumno debe recordar que al trazar datos de desempeño debe trazar suficientes puntos para obtener una buena definición de la curva en la región donde se busca información. Por ejemplo, no hay forma de decir a partir de los tres puntos de datos a continuación dónde podría estar el mínimo.

Referencias

Figura P1: Gris Kindred (2021). “Conjuntos de datos de ejemplo y estilos de trazado”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/intro-hw-1

Figura P2: Gris Kindred (2021). “Incertidumbre de curvatura debido a puntos de datos insuficientes”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/intro-hw-2