1: Introducción a la aerodinámica
- Page ID
- 80914
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Capítulo 1. Introducción a la aerodinámica
1.1 Aerodinámica
La aerodinámica es probablemente el primer tema que viene a la mente cuando la mayoría de la gente piensa en Ingeniería Aeronáutica o Aeroespacial. La aerodinámica es esencialmente la aplicación de teorías clásicas de la “mecánica de fluidos” a flujos externos o flujos alrededor de los cuerpos, y la aplicación principal que viene a la mente para la mayoría de los ingenieros aerodinámicos es el flujo alrededor de las alas.
El ala es la parte más importante de un avión porque sin él no habría sustentación ni avión. La mayoría de la gente tiene alguna idea de cómo funciona un ala; es decir, al hacer que el flujo sobre la parte superior del ala vaya más rápido que el flujo sobre la parte inferior obtenemos una presión menor en la parte superior que en la parte inferior y, como resultado, obtenemos levantamiento. El aeroingeniero necesita saber algo más que esto. El ingeniero aerodinámico necesita saber cómo dar forma al ala para obtener la combinación óptima de elevación y arrastre y momento de lanzamiento para una misión de avión en particular. Además, necesita comprender cómo interactúa la aerodinámica del vehículo con otros aspectos de su diseño y rendimiento. También sería bueno que las fuerzas en el ala no excedieran el límite de carga de la estructura del ala.
Si uno mira suficientes aviones, pasados y presentes, encontrará una amplia variedad de formas de alas. Algunas aeronaves tienen alas cortas y cortas (pequeña envergadura del ala), mientras que otras tienen alas largas y estrechas. Algunas alas son barridas y otras rectas. Las alas pueden tener formas extrañas en sus puntas o incluso accesorios y extensiones como las aletas. Todas estas formas están relacionadas con el propósito y diseño de la aeronave.
Para ver por qué las alas tienen forma como son, necesitamos comenzar por mirar los términos que se utilizan para definir la forma de un ala.
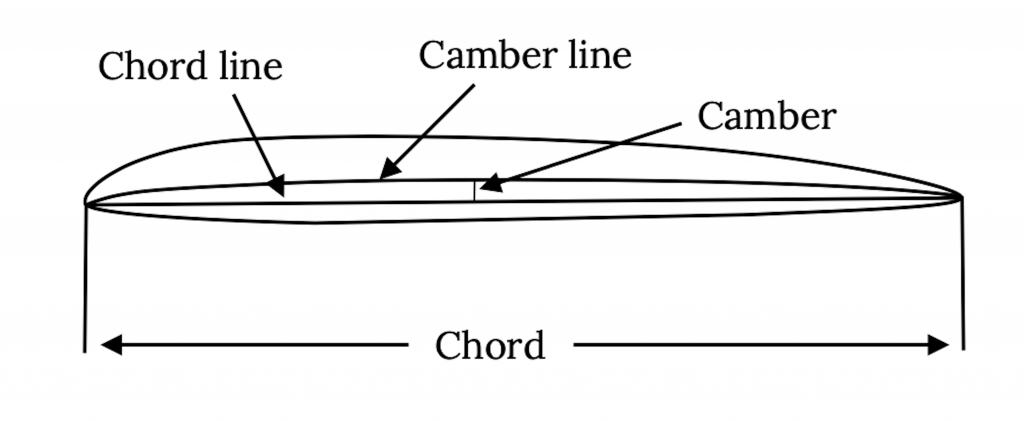
Un corte bidimensional de un corte de ala paralelo a la línea central del fuselaje o cuerpo de la aeronave se llama sección de perfil aerodinámico. Una línea recta desde el borde de ataque de la sección aerodinámica hasta su borde posterior se llama línea de cuerda. La longitud de la línea de cuerda se conoce como el acorde. Una línea dibujada a mitad de camino entre las superficies superior e inferior de la sección aerodinámica se llama línea de curvatura. La distancia máxima entre la línea de curvatura y la línea de cuerda se conoce como la curvatura del perfil aerodinámico y generalmente se enumera como un porcentaje de cuerda. Veremos que la cantidad de curvatura aerodinámica y la ubicación del punto de curvatura máxima son números importantes para definir la forma de un perfil aerodinámico y predecir su desempeño. Para la mayoría de los perfiles aerodinámicos la curvatura máxima es del orden de cero a cinco por ciento y la ubicación del punto de curvatura máxima es entre 25% y 50% de la cuerda desde el borde de ataque del perfil aerodinámico.
Cuando se ve desde arriba de la aeronave, la forma del ala o planform se define por otros términos.
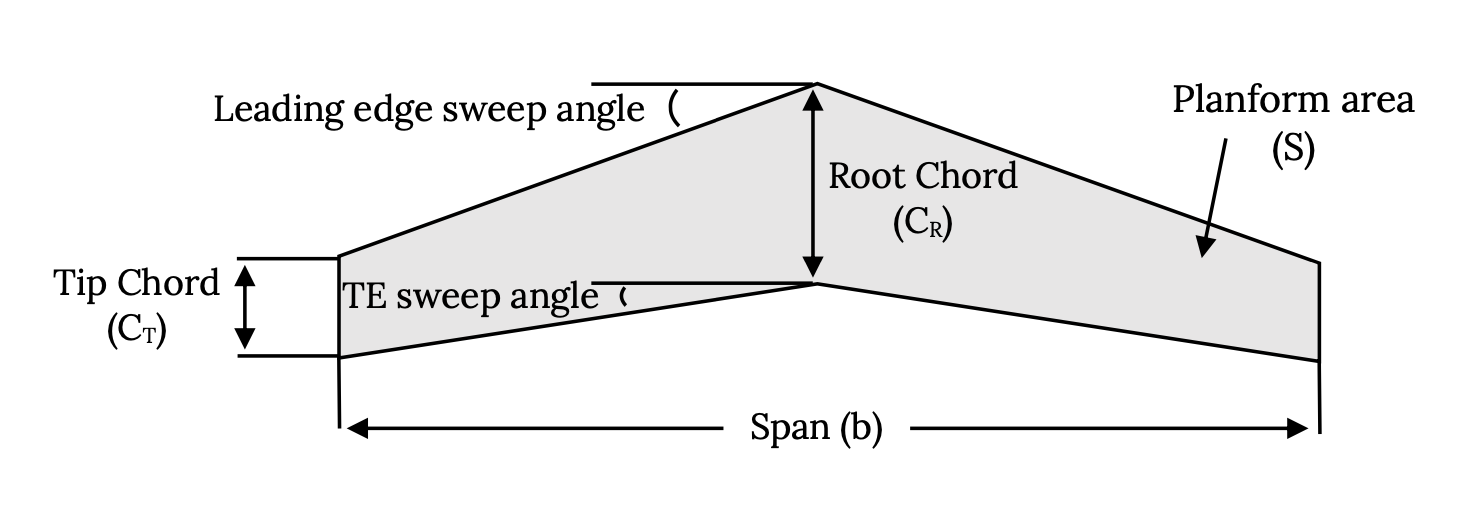
Tenga en cuenta que el área en forma de planta no es la superficie real del ala sino que es “área proyectada” o el área de la sombra del ala. También tenga en cuenta que algunas de las abreviaturas utilizadas no son intuitivas; el lapso, la distancia desde la punta del ala hasta la punta del ala (incluyendo cualquier ancho del fuselaje) se denota con b y al área en forma de planta se le da un símbolo de “S” en lugar de quizás “A”. A los ángulos de barrido se les suele dar un símbolo de lambda (λ).
Otra definición que se basa en la forma en planta de un ala es la Relación de Aspecto (AR).
AR = b 2 /S.
La relación de aspecto también es el span dividido por la “media” o acorde promedio. Más adelante encontraremos que la relación de aspecto es una medida de la eficiencia del ala en vuelos de largo alcance.
Las formas del plano del ala pueden variar considerablemente de un tipo de avión a otro. Los aviones de combate tienden a tener una relación de aspecto baja o alas cortas y rechonchas, mientras que los aviones de transporte de largo alcance tienen formas de alas de mayor relación de aspecto y los aviones de vela tienen tramos de ala aún más altos. Algunas alas son barridas mientras que otras no. Algunas alas tienen formas planas triangulares o “delta”. Si uno mira los últimos 100 años de diseño de alas verá una variedad casi infinita de formas. Algunas de las formas provienen de la optimización aerodinámica, mientras que otras son conformadas para beneficio estructural. Algunos están moldeados como son para sigilo, otros para maniobrabilidad en vuelo aeróbico, y otros solo para satisfacer el deseo de su diseñador de un avión apuesto.
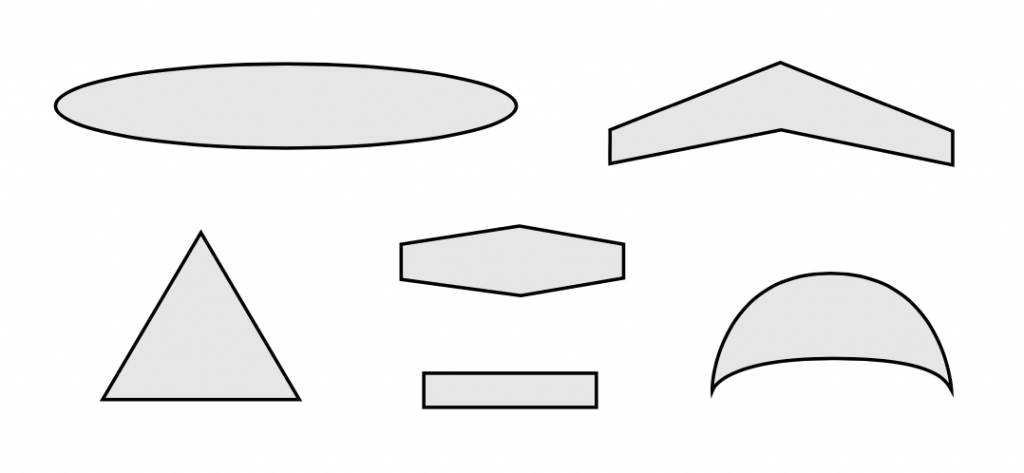
En general, las alas de alta relación de aspecto son deseables para aviones de largo alcance, mientras que las alas de menor relación de aspecto permiten una respuesta de balanceo más rápida cuando la maniobrabilidad es un requisito. Barrir un ala ya sea hacia adelante o hacia atrás reducirá su resistencia a medida que la velocidad del avión se acerca a la velocidad del sonido, pero también reducirá su eficiencia a velocidades más bajas. Las alas delta representan una manera de obtener una combinación de barrido alto y un área grande. La conicidad de un ala para darle una cuerda más baja en las puntas del ala generalmente da un rendimiento algo mejor que un ala no cónica y una conicidad no lineal que le da una forma plana “parabólica” teóricamente dará el mejor rendimiento.
En el siguiente material vamos a echar un vistazo más de cerca a algunas de las cosas mencionadas anteriormente y a sus consecuencias relacionadas con la capacidad de vuelo de un avión.
Antes de echar un vistazo más detallado a la aerodinámica de las alas, primero examinaremos la atmósfera en la que deben operar las aeronaves y veremos algunas de las relaciones básicas que encontramos en la aerodinámica de “hacer”.
1.2 Aire, Nuestro Ambiente de Vuelo
Los aviones operan en aire, un gas compuesto por nitrógeno, oxígeno y varios otros constituyentes. El comportamiento del aire, es decir la manera en que sus propiedades como temperatura, presión y densidad se relacionan entre sí, puede ser descrito por la Ecuación de Estado de Gas Ideal o Perfecto:
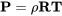
donde P es la presión barométrica o hidrostática, ρ es la densidad y T es la temperatura. R es la constante de gas para el aire. En esta ecuación la temperatura y presión deben darse en valores absolutos; es decir, la temperatura debe estar en Kelvin o Rankine, no Celsius (Centígrados) o Fahrenheit. Por supuesto, todas las unidades deben ser consistentes con las utilizadas en la constante de gas:
1.3 Unidades
Esto nos lleva al tema de las unidades. Es importante que todas las unidades en la ecuación de gas perfecta sean compatibles; es decir, todas las unidades inglesas o todas las unidades SI, y que tengamos cuidado al resolver por, por ejemplo, presión, para asegurarnos de que las unidades de presión salgan como deberían (libras por pie cuadrado en el sistema inglés o Pascales en SI). Desafortunadamente muchos de nosotros no tenemos ni idea de cómo trabajar con unidades.
Es popular en los círculos científicos de Estados Unidos tratar de convencer a todos de que los estadounidenses son las únicas personas en el mundo que usan unidades “inglesas” y las únicas personas en el mundo que no saben cómo usar correctamente las unidades SI. Nada podría estar más lejos de la verdad. Nadie en el mundo realmente usa las unidades SI correctamente en la vida cotidiana. Por ejemplo, el resto del mundo utiliza comúnmente el Kilogramo como unidad de peso cuando en realidad es una unidad de masa. Compran productos en la tienda de abarrotes en Kilogramos, no Newtons. También sería difícil encontrar a alguien en el mundo, incluso en Francia, que sepa que un Pascal es una unidad de presión. Los newtons y los pascales simplemente no se usan en muchos lugares fuera de los libros de texto. En Inglaterra las distancias en las carreteras todavía se dan en millas y las velocidades se dan en mph incluso cuando la gente mide distancias más cortas en metros (o metros), y el gobierno todavía está tratando de que la gente deje de pesar verduras en libras. Hay mucha gente en Inglaterra que sigue dando su peso en “piedras”.
Como ingenieros aeroespaciales encontraremos que, a pesar de lo que dicen muchos de nuestros libros de texto, la mayor parte del trabajo en la industria se realiza en el sistema inglés, no en el SI, y algunos de ellos ni siquiera se hacen en unidades de inglés adecuadas. Las velocidades de los aviones se miden en millas por hora o en nudos, y las distancias a menudo se cotizan en millas náuticas. Se dan presiones a los pilotos en pulgadas de mercurio o en milibares. Las presiones dentro de los motores a reacción y cohetes se miden normalmente en libras-porpulgada cuadrada (psi). Las altitudes de los aviones se citan con mayor frecuencia en pies. La potencia del motor se da en caballos de fuerza y el empuje en libras. Debemos ser capaces de trabajar en el mundo real, así como en el mundo políticamente correcto de la escuela secundaria o universitaria física o química o incluso texto de ingeniería.
Cabe señalar que a lo que en América nos referimos como el sistema de unidades “inglesas”, la gente en Inglaterra llama unidades “imperiales”. Esto puede resultar realmente confuso porque las medidas líquidas “imperiales” son diferentes de las medidas líquidas “americanas”. Un galón “imperial” es un poco más grande que un galón estadounidense y una “pinta” de cerveza en Gran Bretaña no es del mismo tamaño que una “pinta” de cerveza en los Estados Unidos.
Entonces, hay muchos sistemas posibles de unidades en uso en nuestro mundo. Estos incluyen el sistema SI, el sistema inglés basado en libras-masa, el sistema inglés basado en “babosas”, el sistema métrico cgs-y otros. Podemos discutir todos estos en términos de una ecuación muy familiar, la buena F = ma de Isaac Newton. La ley de Newton relaciona unidades así como propiedades físicas y podemos usarla para observar varios sistemas de unidades comunes.
Fuerza = masa x aceleración
1 Newton = 1 kg x 1 medidor de/seg 2
1 libra-fuerza = 1 libra-masa x 32.17 pies/seg 2
1 Dina = 1 gramo x 1 cm/s 2
1 libra-fuerza = 1 babosa x 1 pies/seg 2
El primero y el último de los anteriores son los sistemas con los que necesitamos estar completamente familiarizados; el primero porque es el sistema “ideal” según la mayoría en el mundo científico, y el último porque es el sistema semioficial del mundo de la ingeniería aeroespacial.
En el uso de cualquier sistema de unidades hay tres requisitos básicos:
- Siempre escriba unidades con cualquier número que tenga unidades.
- Trabaja siempre a través de las unidades en ecuaciones al mismo tiempo que trabajas los números.
- Siempre reduzca las unidades finales a su forma más simple y verifique que sean las unidades adecuadas para ese número.
Seguir las sugerencias anteriores eliminaría aproximadamente la mitad de las respuestas incorrectas que se encuentran en la mayoría de las tareas y exámenes de los estudiantes.
Al hacer problemas de ingeniería uno debe llevar a través de las unidades como se describió anteriormente y asegurarse de que las unidades tengan sentido para la respuesta y que la magnitud de la respuesta sea razonable. Los buenos estudiantes hacen esto todo el tiempo mientras que los pobres dejan todo al azar.
La primera parte de esto es simple. Si las unidades en una respuesta no tienen sentido, por ejemplo, si la velocidad para un avión se calcula en 345 pies por libra o si calculamos un peso para ser de 1500 kilogramos por segundo, debería ser fácil reconocer que algo anda mal. Se ha cometido un error fundamental en el seguimiento a través del problema con las unidades y esto debe ser corregido.
La tarea más difícil es reconocer cuando la magnitud de una respuesta es incorrecta; es decir, no está “en el estadio correcto”. Si nos dicen que la velocidad de un automóvil es de 92 metros/seg. o es de 125 pies/seg. ¿Tenemos alguna “sensación” de si estos son razonables o no? ¿Este auto va a exceso de velocidad o no? La mayoría de nosotros no tenemos idea sin hacer algunos cálculos rápidos (estos son 205 mph y 85 mph, respectivamente). ¿Alguno de nosotros conoce nuestro peso en Newtons? ¿Qué es una presión barométrica razonable en la atmósfera en cualquier sistema de unidades?
Entonces, nuestra segunda tarea relacionada con la unidad es desarrollar cierta apreciación por el rango “normal” de magnitudes para las cosas que queremos calcular en nuestro sistema o sistemas de unidades elegidos. ¿Cuál es un rango razonable para el coeficiente de sustentación o coeficiente de arrastre de un ala? ¿Es razonable que los autos tengan 10 veces el coeficiente de arrastre de los aviones?
Con estas precauciones en mente, volvamos y veamos nuestro “medio de trabajo”, el ambiente estándar.
1.4 La Atmósfera Estándar
Dijimos que estábamos iniciando con la Ecuación de Gas Ideal de Estado, P=RT. También haremos uso de la Ecuación Hidrostática, otra relación que ya has visto antes en química y física:
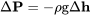
Esto nos dice cómo cambia la presión con la altura en una columna de fluido. Esto nos dice cómo cambia la presión a medida que avanzamos hacia arriba o hacia abajo a través de la atmósfera.
Estas dos ecuaciones, la Ecuación de Estado de Gas Perfecto y la Ecuación Hidrostática, tienen tres variables en ellas: presión, densidad y temperatura. Resolver por estas propiedades en cualquier punto de la atmósfera requiere que tengamos una ecuación más, una que involucre la temperatura. Esto va a requerir nuestra primera suposición. Debemos tener alguna relación que nos pueda decir cómo la temperatura debe variar con la altitud en la atmósfera.
Muchos años de medición y observación han demostrado que, en general, la porción inferior de la atmósfera, donde vuelan la mayoría de los aviones, puede modelarse en dos segmentos, la Troposfera y la Stratosfera. Se encuentra que la temperatura en la troposfera desciende de manera bastante lineal a medida que aumenta la altitud. Esta disminución lineal de la temperatura continúa hasta cerca de 36,000 pies (unos 11,000 metros). Por encima de esta altitud se encuentra que la temperatura se mantiene constante hasta altitudes superiores a 100,000 pies. Esta región de temperatura constante es la parte inferior de la estratosfera. La troposfera y la estratosfera son donde operan los aviones, por lo que necesitamos verlas en detalle.
1.5 La troposfera
Modelamos la caída lineal de temperatura con altitud en la troposfera con una ecuación simple:
T alt = T nivel del mar — Lh
donde “L” se llama la “tasa de lapso”. A partir de más de cien años de mediciones se ha encontrado que una tasa de lapso normal y promedio es:
L = 3.56 o R/1000 ft = 6.5 o K/1000 metros.
Esto a menudo se enseña a los pilotos en una extraña mezcla de unidades como ¡1.98 grados centígrados por mil pies!
La otra cosa que necesitamos es un valor para la temperatura del nivel del mar. Nuestro modelo, también basado en promedios de años de medición, utiliza los siguientes valores del nivel del mar para presión, densidad y temperatura.
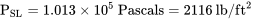
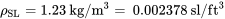
T SL = 288 o K = 520 o R
Entonces, para encontrar la temperatura en cualquier punto de la troposfera utilizamos:
T (o R) = 520 — 3.56 (h),
donde h es la altitud en miles de pies, o
T (o K) = 288 — 6.5 (h)
donde h es la altitud en miles de metros.
Debemos recalcar en este punto que este modelo de temperatura para la Troposfera no es más que un modelo, pero es el modelo que todos en la comunidad aeronáutica y aeroespacial han acordado aceptar y utilizar. La posibilidad de alguna vez ir a la orilla del mar y medir una temperatura de 59 o F es escasas e incluso si encontramos esa temperatura seguramente cambiará en unos minutos. De igual manera, si tuviéramos que enviar un termómetro en un globo en un día cualquiera, la posibilidad de encontrar una “tasa de lapso” igual a la definida como “estándar” es delgada o nula, y, durante el paso de un frente meteorológico, incluso podemos encontrar que la temperatura aumenta en lugar de bajar a medida que nos movemos a altitudes más altas. No obstante, trabajaremos con este modelo y quizás más tarde aprenderemos a hacer correcciones por días no estándar.
Ahora bien, si estamos dispuestos a aceptar el modelo anterior para el cambio de temperatura en la Troposfera, todo lo que tenemos que hacer es encontrar relaciones para contar cómo las otras propiedades, presión y densidad, cambian con la altitud en la Troposfera. Comenzamos con la forma diferencial de la ecuación hidrostática y la combinamos con la ecuación Perfect Gas para eliminar el término de densidad.
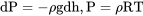
o,
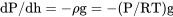
que se reordena para dar
dP/p = — (g/RT) dh.
Ahora sustituimos en la relación de tasa de lapso por la temperatura para obtener
dP/p = {g/ [R (T SL -Lh)]} dh.
Esta es ahora una relación con una sola variable (P) a la izquierda y sólo una (h) a la derecha. Se puede integrar para dar
![PALT/PSL= [Talt/TSL] g/Lr](https://eng.libretexts.org/@api/deki/files/49039/ccf49692af7eedab1919f7cb5a047ffd.png)
De manera similar podemos conseguir una relación para encontrar la densidad a cualquier altitud en la troposfera
![ρAlt/ρSL= [talt/TSL] (g−LR) /LR](https://eng.libretexts.org/@api/deki/files/49040/36ed3218dc8951686055ab7f1631654d.png)
Entonces ahora tenemos ecuaciones para encontrar presión, densidad y temperatura a cualquier altitud en la troposfera. Hay que tener cuidado con las unidades al usar estas ecuaciones. Todas las temperaturas deben estar en valores absolutos (Kelvin o Rankine en lugar de Celsius o Fahrenheit). Los exponentes en las ecuaciones de relación de presión y densidad deben ser sin unidades. ¡Los exponentes no pueden tener unidades!
Podemos usar estas ecuaciones hasta la cima de la Troposfera, es decir, hasta 11,000 metros o 36,100 pies de altitud. Por encima de esa altitud se encuentra la estratosfera donde la temperatura se modela como constante hasta aproximadamente 100,000 pies.
1.6 La estratosfera
Podemos usar el resultado de la ecuación de tasa de lapso de temperatura a 11,000 metros de altitud para encontrar la temperatura en esta parte de la estratosfera.
T estratosfera = 216,5 o K = 389.99 o R = constante
Las ecuaciones para determinar la presión y densidad en la parte de temperatura constante de la estratosfera son diferentes a las de la troposfera ya que la temperatura es constante. Y, dado que la temperatura es constante tanto la presión como la densidad varían de la misma manera.
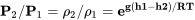
El término a la derecha en la ecuación es “e” o 2.718, evaluado a la potencia mostrada, donde h 1 es los 11,000 metros o 36,100 pies (dependiendo del sistema unitario utilizado) y h 2 es la altitud donde se va a calcular la presión o densidad. T es la temperatura en la estratosfera.
Usando las ecuaciones anteriores podemos encontrar la presión, temperatura o densidad en cualquier lugar donde un avión pueda volar. Es común tabular esta información en una tabla de atmósfera estándar. La mayoría de estas tablas también incluyen la velocidad del sonido y la viscosidad del aire, ambas funciones de la temperatura. A continuación se dan tablas tanto en unidades SI como en inglés.
Cuadro 1.1: Atmósfera estándar en unidades SI
| h (km) | T (grados C) | a (m/seg) | Px10^ (-4) (N/m^2) (pascales) | P (kg/m^3) | u x10^5 (kg/m seg) |
|---|---|---|---|---|---|
| 0 | 15 | 340 | 10.132 | 1.226 | 1.78 |
| 1 | 8.5 | 336 | 8.987 | 1.112 | 1.749 |
| 2 | 2 | 332 | 7.948 | 1.007 | 1.717 |
| 3 | -4.5 | 329 | 7.01 | 0.909 | 1.684 |
| 4 | -11 | 325 | 6.163 | 0.82 | 1.652 |
| 5 | -17.5 | 320 | 5.4 | 0.737 | 1.619 |
| 6 | -24 | 316 | 4.717 | 0.66 | 1.586 |
| 7 | -30.5 | 312 | 4.104 | 0.589 | 1.552 |
| 8 | -37 | 308 | 3.558 | 0.526 | 1.517 |
| 9 | -43.5 | 304 | 3.073 | 0.467 | 1.482 |
| 10 | -50 | 299 | 2.642 | 0.413 | 1.447 |
| 11 | -56.5 | 295 | 2.261 | 0.364 | 1.418 |
| 12 | -56.5 | 295 | 1.932 | 0.311 | 1.418 |
| 13 | -56.5 | 295 | 1.65 | 0.265 | 1.418 |
| 14 | -56.5 | 295 | 1.409 | 0.227 | 1.418 |
| 15 | -56.5 | 295 | 1.203 | 0.194 | 1.418 |
| 16 | -56.5 | 295 | 1.027 | 0.163 | 1.418 |
| 17 | -56.5 | 295 | 0.785 | 0.141 | 1.418 |
| 18 | -56.5 | 295 | 0.749 | 0.121 | 1.418 |
| 19 | -56.5 | 295 | 0.64 | 0.103 | 1.418 |
| 20 | -56.5 | 295 | 0.546 | 0.088 | 1.418 |
| 30 | -56.5 | 295 | 0.117 | 0.019 | 1.418 |
| 45 | 40 | 355 | 0.017 | 0.002 | 1.912 |
| 60 | 70.8 | 372 | 0.003 | 0.00039 | 2.047 |
| 75 | -10 | 325 | 0.0006 | 0.00008 | 1.667 |
Cuadro 1.2: Ambiente estándar en unidades inglesas
| h (pies) | T (grados F) | a (pies/seg) | p (lb/ft^2) | p (slugs/ft^3) | u x 10^7 (sl/pies-seg) |
|---|---|---|---|---|---|
| 0 | 59 | 1117 | 2116.2 | 0.002378 | 3.719 |
| 1,000 | 57.44 | 1113 | 2040.9 | 0.00231 | 3.699 |
| 2,000 | 51.87 | 1109 | 1967.7 | 0.002242 | 3.679 |
| 3,000 | 48.31 | ll05 | 1896.7 | 0.002177 | 3.659 |
| 4,000 | 44.74 | ll02 | 1827.7 | 0.002112 | 3.639 |
| 5,000 | 41.18 | 1098 | 1760.8 | 0.002049 | 3.618 |
| 6,000 | 37.62 | 1094 | 1696 | 0.001988 | 3.598 |
| 7,000 | 34.05 | 1090 | 1633 | 0.001928 | 3.577 |
| 8,000 | 30.49 | 1086 | 1571.9 | 0.001869 | 3.557 |
| 9,000 | 26.92 | 1082 | 1512.9 | 0.001812 | 3.536 |
| 10,000 | 23.36 | 1078 | 1455.4 | 0.001756 | 3.515 |
| ll,000 | 19.8 | 1074 | 1399.8 | 0.001702 | 3.495 |
| 12,000 | 16.23 | 1070 | 1345.9 | 0.001649 | 3.474 |
| 13,000 | 12.67 | 1066 | 1293.7 | 0.001597 | 3.453 |
| 14,000 | 9.1 | 1062 | 1243.2 | 0.001546 | 3.432 |
| 15,000 | 5.54 | 1058 | 1194.3 | 0.001497 | 3.411 |
| 16,000 | 1.98 | 1054 | 1147 | 0.001448 | 3.39 |
| 17,000 | -1.59 | 1050 | 1101.1 | 0.001401 | 3.369 |
| 18,000 | -5.15 | 1046 | 1056.9 | 0.001355 | 3.347 |
| 19,000 | -8.72 | 1041 | 1014 | 0.001311 | 3.326 |
| 20,000 | -12.28 | 1037 | 972.6 | 0.001267 | 3.305 |
| 21,000 | -15.84 | 1033 | 932.5 | 0.001225 | 3.283 |
| 22.000 | -19.41 | 1029 | 893.8 | 0.001183 | 3.262 |
| 23,000 | -22.97 | 1025 | 856.4 | 0.001143 | 3.24 |
| 24,000 | -26.54 | 1021 | 820.3 | 0.001104 | 3.218 |
| 25,000 | -30.1 | 1017 | 785.3 | 0.001066 | 3.196 |
| 26,000 | -33.66 | 1012 | 751.7 | 0.001029 | 3.174 |
| 27,000 | -37.23 | 1008 | 719.2 | 0.000993 | 3.153 |
| 28,000 | -40.79 | 1004 | 687.9 | 0.000957 | 3.13 |
| 29,000 | -44.36 | 999 | 657.6 | 0.000923 | 3.108 |
| 30,000 | -47.92 | 995 | 628.5 | 0.00089 | 3.086 |
| 31,000 | -51.48 | 991 | 600.4 | 0.000858 | 3.064 |
| 32,000 | -55.05 | 987 | 573.3 | 0.000826 | 3.041 |
| 33,000 | -58.61 | 982 | 547.3 | 0.000796 | 3.019 |
| 34,000 | -62.18 | 978 | 522.2 | 0.000766 | 2.997 |
| 35,000 | -65.74 | 973 | 498 | 0.000737 | 2.974 |
| 40,000 | -67.6 | 971 | 391.8 | 0.0005857 | 2.961 |
| 45,000 | -67.6 | 971 | 308 | 0.0004605 | 2.961 |
| 50,000 | -67.6 | 971 | 242.2 | 0.0003622 | 2.961 |
Cuadro 1.2: Atmósfera estándar en unidades inglesas (con't)
| h (pies) | T (grados F) | a (pies/seg) | p (lb/ft^2) | p (slugs/ft^3) | u x 10^7 (sl/pies-seg) |
|---|---|---|---|---|---|
| 60,000 | -67.6 | 971 | 150.9 | 0.000224 | 2.961 |
| 70,000 | -67.6 | 971 | 93.5 | 0.0001389 | 2.961 |
| 80,000 | -67.6 | 971 | 58 | 0.0000861 | 2.961 |
| 90,000 | -67.6 | 971 | 36 | 0.0000535 | 2.961 |
| 100,000 | -67.6 | 971 | 22.4 | 0.0000331 | 2.961 |
| 150,000 | 113.5 | 1174 | 3.003 | 0.00000305 | 4.032 |
| 200,000 | 159.4 | 1220 | 0.6645 | 0.00000062 | 4.277 |
| 250,000 | -8.2 | 1042 | 0.1139 | 0.00000015 | 3.333 |
Una mirada a estas mesas mostrará un par de términos que no hemos discutido. Estas son la velocidad del sonido “a”, y la viscosidad “μ”. La velocidad del sonido es función de la temperatura y disminuye a medida que disminuye la temperatura en la Troposfera. La viscosidad también es una función de la temperatura.
La velocidad del sonido es una medida de la “compresibilidad” de un fluido. El agua es bastante incompresible pero el aire se puede comprimir como podría ser en un sistema de pistón/cilindro. La velocidad del sonido es esencialmente una medida de qué tan rápido puede moverse un sonido o una onda de compresión a través de un fluido. A menudo hablamos de las velocidades de los aviones de alta velocidad en términos de número Mach donde el número Mach es la relación entre la velocidad de vuelo y la velocidad del sonido. A medida que nos acercamos a la velocidad del sonido (Mach One) el aire se vuelve más compresible y se vuelve más significativo escribir muchas ecuaciones que describan el flujo en términos de número de Mach más que en términos de velocidad.
La viscosidad es una medida del grado en que las moléculas del fluido chocan entre sí y transfieren fuerzas a nivel microscópico. Esto se convierte en una medida de “fricción” dentro de un fluido y es un término importante cuando se mira el arrastre de fricción, el arrastre debido a las fuerzas de corte que ocurren cuando un fluido (aire en nuestro caso) se mueve sobre la superficie de un ala o cuerpo en el flujo.
Dos cosas deben señalarse en estas tablas sobre la viscosidad. Primero, las unidades se ven algo extrañas. Segundo, la columna de viscosidad se encabeza con μ X 10 x. Las unidades son las adecuadas para la viscosidad en los sistemas SI e inglés respectivamente; sin embargo, si hablas con un químico o físico sobre la viscosidad probablemente citarán números con unidades de “poise”. El número 10 x en el encabezado de la columna significa que el número que se muestra en la columna se ha multiplicado por 10 x para darle el valor mostrado. Esto, para la mayoría de nosotros, no es intuitivo. Lo que esto significa es que en la versión unitaria inglesa de la tabla Atmósfera Estándar, la viscosidad a nivel del mar tiene un valor de 3.719 veces diez a la menos 7.
Por lo que ahora podemos encontrar las propiedades del aire a cualquier altitud en nuestro modelo o atmósfera “estándar”. Sin embargo, esto es solo un modelo, y de hecho sería raro encontrar un día en el que el ambiente realmente coincida con nuestro modelo. ¿Qué tan útil es esto?
En realidad, este modelo es bastante bueno cuando se trata de variación de presión en la atmósfera porque se basa en la ecuación hidrostática que es físicamente correcta. Por otro lado, la presión al nivel del mar sí varía de un día a otro con los cambios climáticos, ya que el área de preocupación se encuentra bajo los diversos sistemas de alta o baja presión que a menudo se señalan en los mapas meteorológicos. La temperatura representa la mayor oportunidad de variación entre el modelo y la atmósfera real, después de todo, ¿cuántos días al año es la temperatura en la playa 59 o F (520 o R)? La densidad, por supuesto, es una función de la presión y la temperatura, por lo que su “corrección” depende de la de P y T.
A la vista de las cosas, parece que la Atmósfera Estándar es algo así como una fantasía. Por otro lado, sí nos da una idea bastante buena de cómo estas propiedades del aire normalmente deberían cambiar con la altitud. Y, posiblemente podamos hacer correcciones a las respuestas encontradas al usar este modelo corrigiendo la presión real del nivel del mar y la temperatura si es necesario. Además, podríamos definir otras atmósferas “estándar” si nos fijamos en condiciones de vuelo donde las condiciones son excepcionalmente diferentes a las de este modelo. Esto se hace para dar modelos de atmósfera “Arctic Minimum” y “Tropical Maximum”.
Al final, hacemos todos los cálculos aerodinámicos y de rendimiento de la aeronave basados en la atmósfera estándar normal y todas las pruebas de vuelo se realizan en condiciones de presión atmosférica estándar para definir altitudes. El ambiente estándar es nuestro modelo y resulta que este modelo nos sirve bien.
Una forma en que usamos este modelo es determinar nuestra altitud en vuelo.
1.7 Medición de altitud
El piloto de una aeronave necesita conocer su altitud y hay varias formas de medir la altitud de un avión. El radar podría usarse para medir la distancia del avión sobre el suelo. Las señales satelitales del Sistema de Posicionamiento Global pueden determinar la posición del avión, incluida su altitud, en el espacio tridimensional. Estos y algunos otros posibles métodos de determinación de altitud dependen de la operación de uno o más sistemas eléctricos, y si bien es posible que queramos tener un instrumento de este tipo en nuestro avión, también estamos obligados a tener un “altímetro” que no dependa de baterías o generadores para su funcionamiento. Además, la altitud que el piloto necesita conocer es la altura sobre el nivel del mar. La solución obvia es usar nuestro conocimiento de que la presión varía de una manera bastante confiable con la altitud.
Si sabemos cómo varía la presión con la altitud entonces podemos medir esa presión y determinar la altitud sobre un punto de referencia del nivel del mar. En otras palabras, si medimos la presión como 836 libras por pie cuadrado podemos mirar en la mesa de ambiente estándar y encontrar que deberíamos estar a una altitud de 23,000 pies. Entonces todo lo que tenemos que hacer es construir un simple barómetro mecánico y calibrar su esfera para que lea en unidades de altitud en lugar de presión. A medida que disminuye la presión medida, la altitud indicada aumenta de acuerdo con el modelo atmosférico estándar. Esto es, de hecho, cómo los altímetros “simples” como los que a veces se usan en automóviles o bicicletas o incluso aviones “ultra-lite”. Un barómetro mide la presión del aire y en algún tipo de dial o escala, en lugar de unidades de presión, se indican las altitudes equivalentes.
El altímetro “simple”, sin embargo, podría no ser lo suficientemente preciso para la mayoría de los vuelos debido a las variaciones en la presión atmosférica con los cambios del sistema meteorológico. El altímetro simple basaría su lectura en el supuesto de que la presión al nivel del mar es de 2116 psf. Sin embargo, si nos encontramos en una zona de “alta” presión, el altímetro de un avión sentado al nivel del mar percibiría la presión más alta que la estándar e indicaría una altitud algo por debajo del nivel del mar. Por el contrario, en las proximidades de un sistema atmosférico de baja presión el altímetro leería una altitud mayor que el valor real. Si este error fuera solo de unos pocos pies podría no importar, pero en realidad podría resultar en errores de varios cientos de pies en lecturas de altitud. Esto podría llevar al desastre con mal tiempo cuando un piloto tiene que confiar en el altímetro para asegurarse de que el avión despeje los picos de las montañas o se acerque a la pista a la altitud correcta. De ahí que en la actualidad todas las aeronaves utilicen altímetros “sensibles” que permiten al piloto ajustar el instrumento para los cambios de presión debidos a los patrones climáticos atmosféricos.
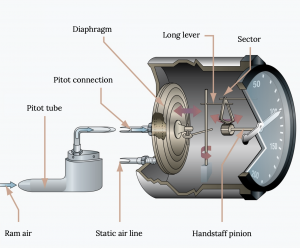
El altímetro sensible, que se muestra en la siguiente figura, tiene una perilla que se puede girar para ajustar la lectura del instrumento para presiones no estándar del nivel del mar. Esto se puede utilizar de dos maneras diferentes en vuelo. Cuando el avión está sentado en el suelo en un aeropuerto, el piloto puede simplemente ajustar la perilla hasta que el altímetro lea la altitud conocida del aeropuerto. En vuelo, el piloto puede escuchar actualizaciones de reportes meteorológicos de aeropuertos cercanos, reportes que incluirán la actual presión barométrica equivalente al nivel del mar, y girar la perilla hasta que los números en una pequeña ventana en la cara del altímetro coincidan con la presión señalada. Estas lecturas suelen darse en unidades de milímetros de mercurio donde 29.92 es estándar del nivel del mar. Ajustar la lectura en la ventana a una presión más alta dará como resultado una disminución en la lectura del altímetro y ajustarla a menor aumentará la indicación de altitud. Con el uso adecuado y oportuno de este ajuste, un buen altímetro debe ser preciso dentro de unos 50 pies.
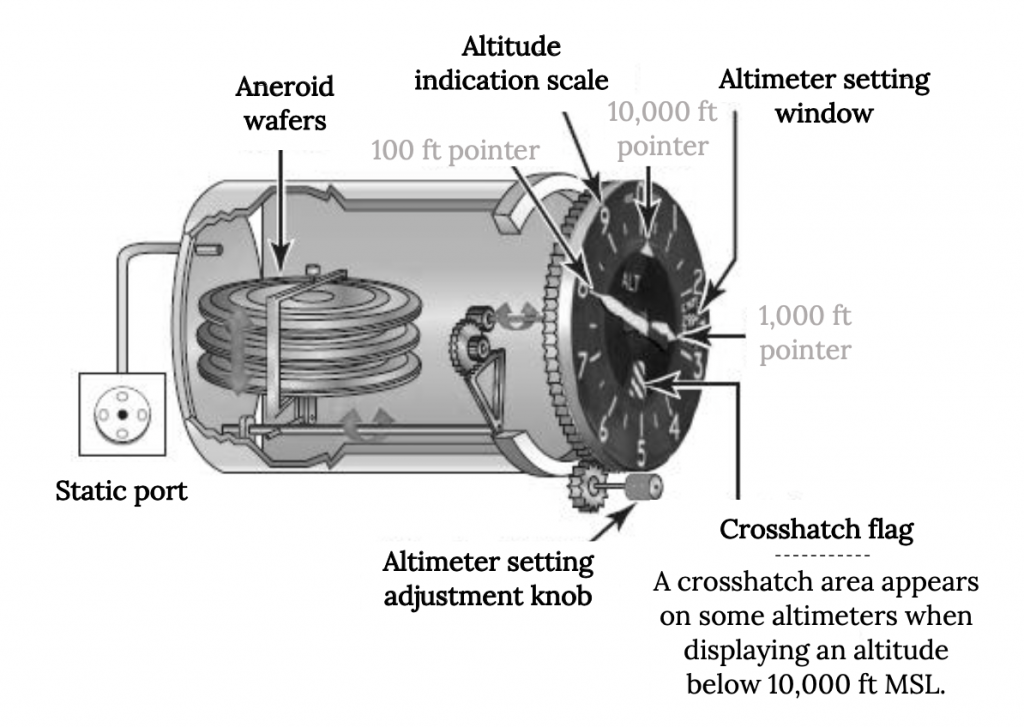
Cabe señalar que también podríamos usar la densidad para definir nuestra altitud y, de hecho, esto podría resultar más significativo en términos de relación con los cambios en el rendimiento de un avión a diversas altitudes de vuelo porque se sabe que el empuje y la potencia del motor son funciones de densidad y la elevación aerodinámica y arrastre son también funciones de densidad. Sin embargo, para “medir” la densidad requeriría medir tanto la presión como la temperatura. Esto podría introducir más error en nuestro uso de la atmósfera estándar para la determinación de altitud que el uso de la presión solo porque la variación de temperatura está mucho más sujeta a un comportamiento no estándar que a la presión. Por otro lado, a veces nos parece valioso calcular nuestra “altitud de densidad” al observar la capacidad de un avión para despegar en una distancia de tierra determinada.
Si estamos en un aeropuerto que está a una altitud de, digamos, 4000 pies y la temperatura es superior a los 44.74 o F que predice la atmósfera estándar (como probablemente sería en verano) encontraríamos que el avión se comporta como si estuviera a mayor altitud y tomará una distancia más larga para llegar a ser aerotransportado de lo que debería a 4000 pies. Los pilotos utilizan una calculadora de tipo regla de cálculo circular o una calculadora electrónica especial para tomar la temperatura real medida y combinarla con la altitud de presión para encontrar la “altitud de densidad”, y esto se puede usar para estimar la distancia de despegue adicional necesaria en relación con las condiciones estándar.
Algunos pueden preguntarse por qué no podemos simplemente usar la temperatura para encontrar nuestra altitud. Después de todo, ¿no era una de nuestras suposiciones básicas que en la Troposfera, la temperatura bajaba linealmente con la altitud? ¿No sería muy fácil sacar un termómetro por la ventana y comparar su lectura con una carta de atmósfera estándar para encontrar nuestra altitud?
Por supuesto, una vez que estemos por encima de la Troposfera esto no serviría de nada ya que la temperatura se vuelve constante a lo largo de miles de pies de altitud, pero ¿por qué no funcionaría en la Troposfera?
Ejercicio de Pensamiento
- Piense y discuta por qué usar la temperatura para encontrar altitud no es una buena idea.
- ¿Por qué la presión es la mejor propiedad a medir para encontrar nuestra altitud?
- Quizás usar densidad para encontrar altitud sería una mejor idea ya que la densidad tiene un efecto directo en el rendimiento del vuelo. Piensa en una razón por la que no tenemos altímetros que midan la densidad del aire.
1.8 Ecuación de Bernoulli
Sin duda te han introducido una relación llamada Ecuación de Bernoulli o el Principio de Bernoulli en algún lugar de un curso previo de Física o Química. Este es el principio que relaciona la presión con la velocidad en cualquier fluido, mostrando esencialmente que a medida que la velocidad de un fluido aumenta su presión disminuye y viceversa. Este principio puede tomar varias formas matemáticas diferentes dependiendo del fluido y su velocidad. Para un fluido incompresible como el agua o para el aire por debajo de aproximadamente 75% de la velocidad del sonido esta relación toma la siguiente forma:
P + ½ ρ V 2 = P 0
presión (hidro) estática + presión dinámica = presión total
[energía interna + energía cinética = energía total]
Esta relación puede pensarse como una medida del equilibrio de las fuerzas de presión en un flujo, o como un balance energético (primera ley de la termodinámica) cuando no hay cambio en la energía potencial o la transferencia de calor.
La ecuación de Bernoulli dice que a lo largo de cualquier trayectoria continua (“aerodinámica”) en un flujo la presión total, P 0, (o energía total) se conserva (constante) y es una suma de la presión estática y la presión dinámica en el flujo. Tanto la presión estática como la presión dinámica pueden cambiar, pero deben cambiar de tal manera que su suma sea constante; es decir, a medida que el flujo acelera la presión disminuye.
* A SSUMESIONES: Es muy importante que conozcamos y entendamos los supuestos que limitan el uso de esta forma de la ecuación de Bernoulli. La ecuación puede derivarse ya sea de la primera ley de la termodinámica (conservación de energía) o de un equilibrio de fuerzas en un fluido a través de lo que se conoce como Ecuación de Euler. Al derivar la forma de la ecuación anterior se hacen algunas suposiciones con el fin de hacer algunas de las matemáticas más simples. Estos involucran cosas como asumir que la densidad es una constante, convirtiéndola en una constante en un paso de integración en la derivación y facilitando la integración. También se asume que la masa se conserva, una suposición aparentemente lógica, pero que tiene ciertas consecuencias en el uso de la ecuación. También se supone que el flujo es “constante”, es decir, la velocidad en cualquier punto del flujo no varía con el tiempo. Otra forma de poner esto es que la velocidad puede variar con la posición en el flujo (de eso es realmente de lo que se trata la ecuación) pero no puede variar con el tiempo.
El supuesto de densidad constante, a la que solemos llamar una suposición de flujo incompresible, significa que tenemos que observar un límite de velocidad. A medida que el aire se acelera y la velocidad se acerca a la velocidad del sonido, su densidad cambia; es decir, se vuelve compresible. Entonces, cuando nuestras velocidades de flujo se acercan demasiado a la velocidad del sonido, se viola la suposición de flujo incompresible y ya no podemos usar esta forma de la ecuación de Bernoulli. ¿Cuándo se convierte eso en un problema?
Algunos libros de texto de mecánica de fluidos utilizan una relación matemática en serie para observar la relación entre la velocidad o el número de Mach (el número Mach, la velocidad dividida por la velocidad del sonido, es realmente una mejor medida de compresibilidad que la velocidad sola) y utilizan esto para demostrar que la suposición de flujo incompresible es no válido por encima de un número Mach de aproximadamente 0.3 o 0.3 veces la velocidad del sonido. Esto es una buena matemática pero no tan buena física. Lo importante no es cómo funcionan las matemáticas sino cómo cambia la relación entre las dos presiones en la ecuación de Bernoulli a medida que aumenta la velocidad o el número de Mach. Examinaremos esto en un ejemplo posterior para demostrar que en realidad estamos bastante seguros al usar la forma incompresible de la ecuación de Bernoulli hasta algo así como el 75% de la velocidad del sonido.
Los otros supuestos importantes en esta forma de ecuación de Bernoulli son los de flujo constante y conservación de masa. El flujo constante significa más o menos lo que parece; la ecuación solo es capaz de dar cuenta de los cambios en la velocidad y la presión con la posición en un campo de flujo. Se asumió que el flujo es exactamente el mismo en cualquier momento.
El supuesto de conservación masiva realmente se relaciona con mirar lo que se llama “agiliza” en un flujo. Estos pueden pensarse a nivel básico como caminos de flujo o carreteras que siguen o delinean el movimiento del flujo. La conservación de masa implica que en cualquier punto a lo largo de esos caminos o entre dos líneas de corriente cualquiera, el flujo másico entre las líneas de flujo (en el camino) es el mismo que en cualquier otro punto entre las mismas dos líneas de corriente (o a lo largo de la misma trayectoria).
El resultado final de esta suposición de conservación masiva es que la ecuación de Bernoulli solo se garantiza que se mantenga verdadera a lo largo de una línea o trayectoria en un flujo. Sin embargo, podemos extender el uso de la relación a cualquier punto del flujo si todo el flujo a lo largo de todas las líneas de corriente (o caminos) en algún punto de referencia aguas arriba (en “∞”) tiene la misma energía total o presión total.
Entonces, podemos usar la ecuación de Bernoulli para explicar cómo un ala puede producir sustentación. Si el flujo sobre la parte superior del ala es más rápido que el de la parte inferior, la presión en la parte superior será menor que la de la parte inferior y la diferencia de presión resultante producirá una elevación. El estudio de la aerodinámica se trata realmente de predecir tales cambios en la velocidad y la presión alrededor de diversas formas de alas y cuerpos. Los aerodinamistas escriben ecuaciones para describir la forma en que las velocidades del aire cambian alrededor de las formas prescritas y luego las combinan con la ecuación de Bernoulli para encontrar las presiones y fuerzas resultantes.
Veamos el uso de la ecuación de Bernoulli para el caso que se muestra a continuación de un ala que se mueve por el aire a 100 metros/seg. a una altitud de 1km.
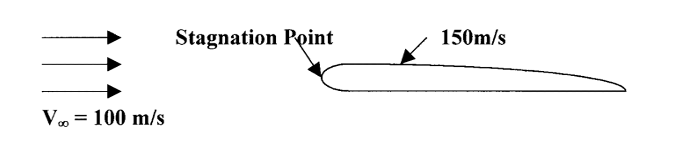
Queremos encontrar la presión en el borde de ataque del ala donde el flujo llega a descansar (el punto de estancamiento) y en un punto sobre el ala donde la velocidad se ha acelerado a 150 m/s.
Primero, tenga en cuenta que el caso del ala que se mueve por el aire ha sido retratado como uno de un ala estacionaria con el aire moviéndose más allá de ella a la velocidad deseada. Este es un procedimiento estándar en el trabajo de problemas aerodinámicos y se puede demostrar que las respuestas que se encuentran utilizando este método son las correctas. Esencialmente, dado que el proceso de usar la ecuación de Bernoulli es uno de mirar la conservación de la energía, no importa si estamos analizando el movimiento (energía cinética) involucrado como movimiento del cuerpo o movimiento del fluido.
Ahora pensemos en el problema presentado anteriormente. Sabemos algo sobre el flujo en tres puntos:
Pues frente al ala tenemos lo que se llama “corriente libre” o flujo no perturbado, uniforme. Designamos propiedades en este flujo con un subíndice infinito [∞]. Podemos escribir la ecuación de Bernoulli aquí como:
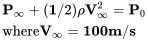
Tenga en cuenta que es en este punto, el “flujo libre” donde todo el flujo es uniforme y tiene la misma energía total. Si en este punto el flujo no era uniforme, quizás porque estaba cerca del suelo y la velocidad aumenta con la distancia hacia arriba del suelo, no podríamos suponer que cada “aerodinámica” tuviera un valor diferente de presión total (energía).
Al frente del ala tendremos un punto donde el flujo vendrá a descansar. Llamamos a este punto el “punto de estancamiento” si podemos suponer que el flujo se desaceleró y se detuvo sin pérdidas significativas. Aquí la velocidad del flujo sería cero. Podemos escribir la ecuación de Bernoulli aquí como:
P estancamiento + 0 = P 0
En este punto el flujo se ha acelerado a 150 m/s y podemos escribir la ecuación de Bernoulli como:
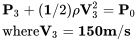
Ahora sabemos que como el flujo sobre el ala es continuo (se conserva la masa) la presión total (P 0 ) es la misma en los tres puntos y esto es lo que usamos para encontrar la información faltante. Para ello debemos entender cuáles de estas presiones (si las hay) son conocidas por nosotros como presiones hidrostáticas atmosféricas y entender que podemos suponer que la densidad es constante siempre y cuando estemos seguros por debajo de la velocidad del sonido.
Inicialmente sabemos que la presión en la atmósfera es aquella en la tabla de atmósfera estándar para una altitud de 1 km o 89870 Pascales y que la densidad a esta altitud es de 1.112 kg/m 3. Al observar el problema, el lugar más lógico para que se apliquen las condiciones de atmósfera estándar es en la ubicación de “arroyo libre” porque aquí es donde existe el flujo no perturbado. De ahí
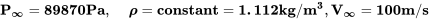
Y, usando estos en la ecuación de Bernoulli en la ubicación del flujo libre calculamos una presión total
P 0 = 95430 Pa
Ahora que hemos encontrado la presión total podemos utilizarla en cualquier otra ubicación del flujo para encontrar las otras propiedades desconocidas.
En el punto de estancamiento
P estancamiento = P 0 = 95430 Pa
En el punto donde la velocidad es de 150 m/s podemos reorganizar la ecuación de Bernoulli para encontrar
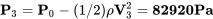
Como comprobación debemos confirmar que la presión estática (P 3) en este punto es menor que la presión estática de corriente libre (P) ya que aquí la velocidad es mayor y también confirmar que las presiones estáticas en todas partes del flujo son menores que la presión de estancamiento.
Ahora repasemos los pasos para trabajar cualquier problema con la ecuación de Bernoulli. Primero debemos bosquejar el flujo y anotar todo lo que sabemos en diversos puntos de ese flujo. Segundo debemos escribir la ecuación de Bernoulli en cada punto del flujo donde o conocemos información o queremos saber algo. Tercero debemos evaluar cuidadosamente qué presión, en su caso, se puede obtener de la mesa de atmósfera estándar. Cuarto debemos mirar todos estos puntos en el flujo y ver qué punto nos da suficiente información para resolver para la presión total (P 0). Finalmente usamos este valor de P 0 en la ecuación de Bernoulli en otros puntos del flujo para encontrar los otros términos faltantes. Intentar saltarse cualquiera de los pasos anteriores puede llevar a errores para la mayoría de nosotros.
Uno de los problemas más comunes que tiene la gente al trabajar con la ecuación de Bernoulli en un problema como el anterior es asumir que el punto de estancamiento es el lugar para iniciar la solución del problema. Miran los tres puntos del flujo y asumen que el punto de estancamiento debe ser el lugar donde se sabe todo. Después de todo, ¿la velocidad en el punto de estancamiento no es igual a cero? ¿No significa esto que la presión estática y la presión total son las mismas aquí? ¿Y qué otra conclusión se puede sacar que suponer que esta presión debe ser entonces la presión atmosférica?
Bueno, la respuesta a las dos primeras preguntas es “sí” pero no sigue un tercer “sí”. Lo que se sabe en el punto de estancamiento es que el término de presión estática en la ecuación es ahora la presión estática en un punto de estancamiento y por lo tanto se llama la presión de estancamiento. Y, como la velocidad es cero, la presión de estancamiento es igual a la presión total en el flujo. Ninguna de estas presiones, sin embargo, es la presión atmosférica.
¿Por qué la presión en el punto de estancamiento no es la presión en la atmósfera? Bueno, aquí es donde nuestra sustitución de un flujo móvil y un ala estacionaria por un ala móvil en un fluido estacionario termina causándonos cierta confusión. En realidad, este punto de estancamiento es donde el ala está colisionando de frente con el aire por el que se está precipitando . La presión aquí, la presión de estancamiento, debe ser igual a la presión en la atmósfera más la presión causada por la colisión entre el ala y el fluido; es decir, debe ser mayor que la presión atmosférica.
Nuestro enfoque de modelar el flujo de un ala que se mueve a través de la atmósfera estacionaria como un flujo móvil alrededor de un ala estacionaria hace que sea más fácil trabajar con la ecuación de Bernoulli en general; sin embargo, debemos tener en cuenta que es un modelo sustituto y alterar nuestra forma de mirarlo adecuadamente. En este modelo la presión hidrostática no es la presión donde el aire es “estático”, es, más bien, la presión donde el flujo está “intacto”. Esto es en las condiciones de “corriente libre”, el punto aguas arriba del cuerpo (ala, en este caso) donde el flujo aún no ha sentido la presencia del ala. Aquí es donde existe la atmósfera intacta. Entre ese punto y el ala misma el flujo tiene que cambiar de dirección y velocidad a medida que se mueve alrededor del cuerpo, por lo que en ningún otro lugar del campo de flujo la presión será la misma que en la atmósfera no perturbada.
1.9 Medición de la velocidad del aire
Ahora que sabemos algo sobre la ecuación de Bernoulli podemos mirar otro uso de la relación, la medición de la velocidad del aire. Reordenando la ecuación podemos escribir:
![V= [2 (P0−P) /ρ] 1/2](https://eng.libretexts.org/@api/deki/files/49048/2bed6fe6384bddfe4806b2880c5a1bd7.png)
Entonces, si conocemos las presiones totales y estáticas en un punto y la densidad en ese punto podemos encontrar fácilmente la velocidad en ese punto. Todo lo que necesitamos es alguna manera de medir o de otra manera encontrar estas cantidades.
Podemos encontrar la presión total (P 0) simplemente insertando un tubo abierto de algún tipo en el flujo para que apunte hacia el flujo que se aproxima y luego se conecte a un manómetro de algún tipo.

La presión estática se puede encontrar de manera similar pero el flujo debe ir paralelo a las aberturas en el tubo o superficie.
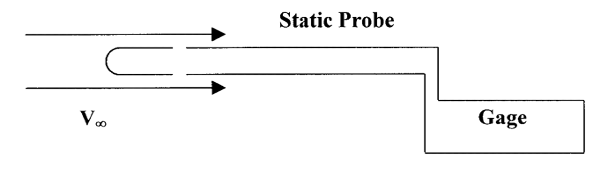
En un avión solemos montar un tubo p itot en algún lugar del ala o nariz de la aeronave donde generalmente apuntará al flujo no perturbado y no estará detrás de una hélice. La lectura de presión estática en un avión normalmente se toma a través de un agujero colocado en algún punto del costado del avión donde el flujo tendrá la misma presión estática que el flujo de transmisión libre en lugar de usar una sonda estática separada. Este punto generalmente se determina en las pruebas de vuelo. Por lo general, hay un puerto estático en ambos lados del plano conectado a un solo tubo a través de una conexión en “T”. El puerto estático parece una pequeña placa circular con un agujero en su centro. Uno de los trabajos requeridos del piloto en su inspección previa al vuelo de la aeronave es asegurarse de que tanto el tubo pitot como los puertos estáticos estén libres de obstrucción, tarea particularmente importante en la primavera del año cuando a los insectos les gusta arrastrarse en pequeños agujeros y construir nidos.
En un túnel de viento y en otras aplicaciones experimentales, a menudo utilizamos un solo instrumento para medir presiones totales y estáticas. Este instrumento se denomina tubo p itot-estático y es simplemente una combinación de las dos sondas mostradas anteriormente.
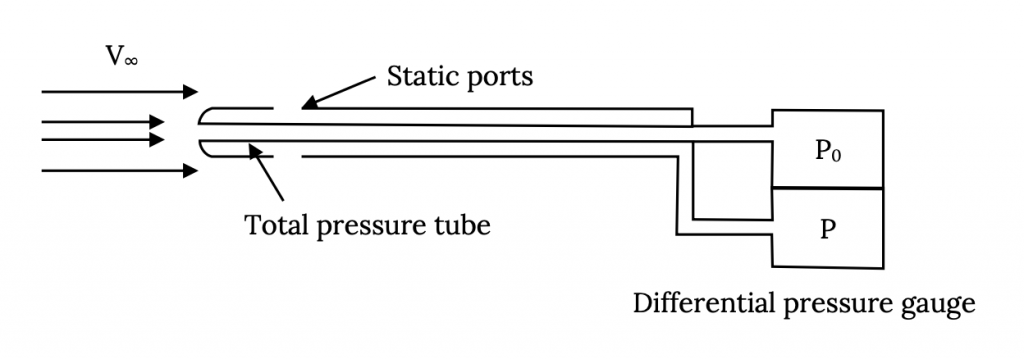
Tanto en el caso de laboratorio como en el de la aeronave es la diferencia en las dos presiones, P 0 — P, lo que queremos saber y esto se puede medir con varios tipos diferentes de dispositivos que van desde un manómetro líquido “U-tube” hasta un sofisticado medidor electrónico. En una aeronave, donde no queremos que nuestro conocimiento de la velocidad aerodinámica dependa de una fuente de electricidad y donde un manómetro líquido sería engorroso, la diferencia de presión se mide mediante un dispositivo mecánico llamado barómetro aneroide.
Pero volvamos y veamos la ecuación utilizada para encontrar la velocidad y ver si esto causa algún problema.
![V= [2 (P0−P) /ρ] 1/2](https://eng.libretexts.org/@api/deki/files/49048/2bed6fe6384bddfe4806b2880c5a1bd7.png)
Esto demuestra que también necesitamos conocer la densidad si queremos encontrar la velocidad. En el laboratorio encontramos la densidad con bastante facilidad midiendo la presión barométrica y la temperatura y calculando la densidad usando la Ley de Gas Ideal,
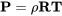
o,
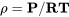
y, usando esto podemos encontrar la velocidad aérea exacta o “verdadera”.
En un avión queremos simplicidad y confiabilidad, y si bien podríamos pedirle al piloto o alguna computadora de vuelo que mida la presión y la temperatura, luego calcular la densidad, luego ponerla en la ecuación de Bernoulli para calcular la velocidad del aire, esto parece un poco oneroso y, por supuesto, el uso de computadoras o calculadoras podría depender de la electricidad. De ahí que no solemos tener un instrumento en una aeronave que muestre la verdadera velocidad aérea; en su lugar elegimos simplemente medir la diferencia en las dos presiones anteriores usando un instrumento mecánico y luego calibrar ese instrumento para mostrar lo que llamamos el indicado a irspeed, una medición de la velocidad basada en el supuesto de densidad del nivel del mar.
![Vind= [2 (P0−P) /ρSL] 1/2](https://eng.libretexts.org/@api/deki/files/49053/fa2b7bd3ec33a2a6751ed9a436bf3b03.png)
Otro nombre para el indicado un irspeed es el “nivel del mar equivalente a irspeed”, la velocidad que existiría para la diferencia medida en presión estática y total si la aeronave estuviera al nivel del mar.
Las velocidades aéreas verdaderas e indicadas están directamente relacionadas por la raíz cuadrada de la relación entre el nivel del mar y las densidades verdaderas.
![Vtrue=Vind [ρSL/ρALT] 1/2](https://eng.libretexts.org/@api/deki/files/49054/7142c648c3da67362dfd32d66af07f4b.png)
El indicador de velocidad aérea de una aeronave mide entonces la velocidad aérea indicada y no la velocidad aérea verdadera. Es un instrumento sellado con la presión estática que va al recipiente del instrumento y la presión total conectada a un barómetro aneroide dentro del contenedor. A medida que cambia la diferencia en estas dos presiones, las agujas indicadoras en la cara del instrumento se mueven sobre un dial marcado, no para un rango de presiones, sino para un rango de velocidades. Cada uno de estos instrumentos se calibra cuidadosamente para garantizar una medición precisa de la velocidad aerodinámica indicada.
Entonces, así como encontramos que el altímetro en un avión mide la altitud incorrecta a menos que seamos capaces de ajustarla correctamente, el indicador de velocidad aérea no mide la velocidad real del aire. ¿Esto es un problema para nosotros?
Resulta que, en lo que respecta al rendimiento de la aeronave; es decir, su capacidad para despegar a cierta distancia, para subir a cierta velocidad, etc., en realidad depende de la velocidad aerodinámica indicada más que de la verdadera velocidad aérea. Sí, queremos conocer la verdadera velocidad aérea para saber qué tan rápido vamos realmente y para fines relacionados con la planificación de vuelos, pero en cuanto a saber la velocidad a la que rotar al despegar, la mejor velocidad a la que subir o deslizarse, y así sucesivamente, estamos mejor usando la velocidad aérea indicada.
La velocidad aérea indicada, ya que se supone que la densidad siempre son condiciones del nivel del mar, es realmente una función solo de la diferencia en las presiones totales y estáticas, P 0 — P, que sabemos por la ecuación de Bernoulli es igual a:
y vamos a encontrar que los términos de la derecha, la presión dinámica, es un término muy importante para dar cuenta de las fuerzas sobre un cuerpo en un fluido. En otras palabras, el comportamiento del avión en vuelo depende mucho más de la presión dinámica que solo de la velocidad del aire.
Ejemplo: Veamos la diferencia entre velocidad aérea verdadera e indicada solo para tener una idea de cuán grande podría ser esta diferencia. Vamos a elegir una altitud de 15,000 pies y ver cuáles serían los dos valores de velocidad aérea si el sistema pitot-static está expuesto a una diferencia de presión de 300 libras-por-pie cuadrado (psf). La densidad en la atmósfera estándar para 15,000 pies es 0.001497 sl/ft 3 mientras que a nivel del mar es 0.002378 sl/ft 3.
![Vind= [2 (P0−P) /ρSL] 1/2 = 502 pies/seg](https://eng.libretexts.org/@api/deki/files/49057/68fe8b14eb75b3e86ecbd2c9266d14f2.png)
![Vtrue=Vind [ρSL/ρAlt] 1/2=633ft/seg.](https://eng.libretexts.org/@api/deki/files/49058/31e5c5e6e988a976da360f4a2c550fbf.png)
Entonces la diferencia en estas dos lecturas puede ser significativa, pero eso está bien. Utilizamos la velocidad aérea indicada para volar el avión y utilizamos la verdadera velocidad aérea al encontrar el tiempo para el viaje. Tenga en cuenta que al trabajar los problemas de ecuación de Bernoulli, como al encontrar las variaciones en las presiones y la velocidad alrededor de un ala, siempre se quiere usar la verdadera velocidad del aire y las presiones y densidad reales a la altitud.
Por último, mientras se trata del tema de la velocidad aérea, debemos señalar que aunque a menudo calculamos la velocidad de una aeronave o ala en unidades de pies/seg. o metros/seg., la mayoría de los indicadores de velocidad aérea mostrarán la velocidad del aire en unidades de millas por hora o nudos. El nudo es una unidad de velocidad bastante antigua utilizada durante siglos por los marineros y una vez medida cronometrando una cuerda anudada cuando se bajaba sobre el costado de un barco hacia el mar que fluye.
Un nudo es una milla náutica por hora y una milla náutica es una fracción establecida de la circunferencia terrestre. En relación con unidades inglesas más familiares:
1 nudo (kt) = 1.15 mph
1 milla náutica (nm) = 1.15 millas “estatuto” (mi).
Es una práctica común en todas partes del mundo que nuestros sistemas de unidades políticamente correctos sean totalmente ignorados y que se haga todo el planeamiento de vuelo y vuelo usando unidades de nudos y millas náuticas para velocidad y distancia.
1.10 Ecuación de Bernoulli para flujo compresible
La forma de la ecuación de Bernoulli que hemos estado usando es para flujo incompresible como se ha señalado varias veces. ¿Y si el flujo no es incompresible?
Si la ecuación de Bernoulli se derivara sin hacer la suposición de densidad de aire constante saldría en una forma diferente y sería una relación entre las presiones y el número de Mach. La relación también tendría otro parámetro en ella, un término llamado gamma (γ). Gamma es simplemente un número para un gas dado y el número depende del número de átomos en la molécula de gas, ya sea monoatómico o diatómico, etc. El aire es realmente una mezcla de gases pero, en general, se considera un gas diatómico. Su valor de gamma es 1.4.
[Otro nombre para gamma es la “relación de calores específicos” o el calor específico a presión constante dividido por el calor específico a densidad constante. Estos calores específicos son una medida de la manera en que el calor se transfiere en un gas bajo ciertas restricciones (presión constante o densidad) y esto, a su vez, depende de la composición molecular del gas. En algunos otros campos, Termodinámica por ejemplo, se usa la letra “k” para esta relación en lugar de γ.]
Cuando un flujo debe considerarse compresible esta relación entre presiones y velocidad o el número de Mach toma la siguiente forma:
(P 0 /P) = {1 + [(γ-1) /2] M 2} [(γ-1)/(γ) ]
Si usa tanto esta ecuación como la forma incompresible de la ecuación de Bernoulli para resolver la presión total para velocidades dadas de cero a 1000 pies/seg., usando las condiciones del nivel del mar y la velocidad del sonido al nivel del mar para encontrar el número de Mach asociado a cada velocidad, y luego comparar los compresibles y valores incompresibles de la presión total (P 0) encontrará poco más de 2% de diferencia a 700 pies/seg. y 5% a 900 pies/seg. En otras palabras, ¡el uso de la ecuación incompresible de Bernoulli para encontrar relaciones de presión y velocidad es bastante razonable hasta velocidades de alrededor del 75% de la velocidad del sonido!
1.11 Fuerzas en un Fluido
Arriba se señaló que el comportamiento de un avión en vuelo depende de la presión dinámica más que de la velocidad o la velocidad solo. En otras palabras, es una cierta combinación de densidad y velocidad y no solo densidad o velocidad sola lo que es importante para la forma en que vuela un avión o un cohete. Una pregunta que podría hacerse es si existen otras combinaciones de propiedades de los fluidos que también tienen una influencia importante en las fuerzas aerodinámicas.
Ya hemos mirado uno de estos, el número Mach, una combinación de la velocidad y la velocidad del sonido. ¿Por qué el número Mach es una combinación “única” de propiedades? ¿Hay otros que son igual de importantes?
Hay una manera bastante simple de echar un vistazo a cómo tales combinaciones de parámetros de flujo de fluido se agrupan para influir en las fuerzas y momentos en un cuerpo en ese flujo. En textos más sofisticados esto se encuentra a través de un proceso conocido como “análisis dimensional”, y en libros donde el autor estaba más decidido a demostrar su destreza matemática que en enseñar una comprensión de la realidad física, el proceso utiliza algo llamado el “Teorema de Buckingham-Pi”. Aquí, solo nos contentaremos con una descripción del proceso más simple.
Si miramos las propiedades en un fluido y en otros lugares que causan fuerzas en un cuerpo como un avión en vuelo podríamos fácilmente nombrar varias cosas como densidad, presión, el tamaño del cuerpo, la gravedad, la “adherencia” o “viscosidad” del fluido y así sucesivamente. Como resulta que podríamos decir con bastante facilidad que la mayoría de las fuerzas en un avión o cohete en vuelo son de alguna manera funciones de las siguientes cosas:
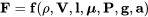
donde,
ρ = densidad
V = velocidad
l = una longitud o tamaño representativos del cuerpo
μ = viscosidad
P = presión
g = gravedad (peso)
a = velocidad del sonido
Se debe considerar la viscosidad para dar cuenta de la fricción entre el flujo y el cuerpo y se incluye la velocidad del sonido porque en algún lugar hemos escuchado que hay cosas como grandes aumentos de arrastre a velocidades cercanas a la velocidad del sonido.
Realmente no sabemos en este punto exactamente qué tan general ser al mirar estos términos. Por ejemplo, ya sabemos por la ecuación de Bernoulli que lo importante es la velocidad al cuadrado y no solo la velocidad, al menos en algunos casos. Y, podríamos esperar que en lugar de longitud es longitud cuadrada (área) lo que es importante en la producción de fuerzas ya que sabemos que las fuerzas provienen de una presión que actúa sobre un área. Entonces, seamos completamente generales y digamos lo siguiente:
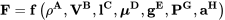
Nuestro simple análisis no busca encontrar relaciones o números exactos sino solo las dependencias funcionales correctas o combinación de parámetros. El análisis es realmente solo cuestión de equilibrar las unidades en los dos lados de la ecuación. En el lado izquierdo tenemos unidades de fuerza (libras o Newtons) donde sabemos que una libra es igual a una babosa por un pies/seg. 2 o que un Newton es un kilogramo-metro por segundo 2. Entonces, la combinación de todas las unidades inherentes a todos los términos en el lado derecho de la ecuación también debe salir en estas mismas combinaciones de unidades exactas que se encuentran en el lado izquierdo de la ecuación. Es decir, cuando todas las unidades se contabilizan en el lado derecho de la ecuación se deben combinar para tener unidades de fuerza;
(sl) 1 (ft) 1 (seg) -2 o (masa) 1 (longitud) 1 (tiempo) -2.
Entonces, en este juego de análisis dimensional el procedimiento es reemplazar cada término físico en ambos lados de la ecuación con sus propias unidades. Entonces podemos simplemente sumar todos los exponentes en ambos lados y escribir ecuaciones que relacionen potencias unitarias. Por ejemplo, a la izquierda tenemos unidades de masa (babosas o kg) a la primera potencia. A la derecha hay varios términos que también tienen unidades de masa en ellos y sus exponentes deben sumar para igualar el de la izquierda.
sl 1 = (sl A) (sl D) (sl G)
o ya que los exponentes agregan:
1 = A + D + G
Podemos hacer las mismas matemáticas para las otras unidades de longitud y tiempo y obtener dos relaciones más entre los exponentes:
1 = -3A + B + C — D + E — G + H
-2 = -B — D — 2E — 2G — H
Estas tres ecuaciones de exponentes unitarios se pueden resolver entonces en términos de tres de las “incógnitas”, A, B y C.
A = 1 — D — G
B = 2 — D — 2E — 2G — H
C = 2 — D + E
Entonces, donde teníamos densidad a la potencia A, o unidades de (sl/ft 3) A, ahora tenemos:
(sl/ft 3) A = (sl) (sl) -D (sl) -G (ft) -3 (ft) 3D (ft) 3G.
Esto lo hacemos con cada término a la derecha de la relación funcional y luego reordenamos los términos, agrupando todos los términos con el mismo exponente de letras y observando las agrupaciones resultantes. Obtendremos:
Entonces, ¿qué nos dice esto? Nos dice que son las agrupaciones de flujo y parámetros corporales a la derecha las que son importantes en lugar de los parámetros individuales para determinar cómo se comporta un cuerpo en un flujo. Examinemos cada uno.
El primer término a la derecha es el único que no tiene exponente indefinido. La ecuación esencialmente dice que una de las cantidades físicas que influye en la producción de fuerzas sobre un cuerpo en un fluido es esta combinación de densidad, velocidad al cuadrado y alguna área (longitud al cuadrado).
Si la fuerza es una función de esta combinación de términos es igual de fácil una función de este grupo dividida por dos; es decir,
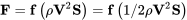
Tenga en cuenta que hemos utilizado la letra “S” para el área. Esto puede parecer una elección extraña ya que en otros campos es común usar S para una distancia; sin embargo, es convencional en aerodinámica usar S para un “área representativa”. El área realmente utilizada es, como su nombre lo indica, un representante de la aerodinámica del cuerpo. En un avión, el área dominante para el levantamiento y arrastre es el ala, y S se convierte en el “área planforme” del ala. En un misil el área frontal se usa comúnmente para S como es el caso de los automóviles y muchos otros objetos.
Lo segundo que notamos es que el término a la derecha es ahora la presión dinámica multiplicada por el área representativa. Por lo que hemos verificado que la presión dinámica es de hecho muy importante para influir en el rendimiento de un vehículo en un fluido.
Si nos fijamos en esta agrupación de términos:
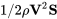
observamos que tiene unidades de fuerza (presión multiplicada por un área). Esto quiere decir que todas las unidades del lado derecho de nuestra ecuación están en este término. Las otras combinaciones de parámetros en el lado derecho de nuestra ecuación deben ser inunitarias. Esto es inmediatamente obvio en un caso, V/a, donde tanto el numerador como el denominador son velocidades y se puede verificar en todos los demás mirando sus unidades. ¡Deberíamos reconocer V/a como el número Mach!
Ahora reescribimos la ecuación:
Esto dice que la combinación sin unidades de términos a la izquierda es de alguna manera una función de las cuatro combinaciones de términos de la derecha. ¿Cuáles son estos términos y qué papel juegan en la producción de fuerzas sobre un cuerpo en un fluido?
1.12 Coeficientes de fuerza
Primero veamos el término de la izquierda. Este término sin unidades nos dice la forma correcta de “no dimensionalizar” las fuerzas fluidas. En lugar de hablar de elevación hablaremos de un coeficiente de elevación sin unidad, C L:
![CL=L/ [1/2ρV2S]](https://eng.libretexts.org/@api/deki/files/49065/85e319046f8d0df2c7df479fc624b42c.png)
También hablaremos de un coeficiente de arrastre no dimensional, C D:
![CD=D/ [1/2ρV2S]](https://eng.libretexts.org/@api/deki/files/49066/c4fdf9de638f3fa23aa3dd895459005b.png)
Utilizamos estos “coeficientes” sin unidades en lugar de las propias fuerzas por dos razones. Primero, son agradables porque no tienen unidades y no necesitamos preocuparnos por el sistema de unidades en el que estamos trabajando. Si un ala tiene un coeficiente de sustentación de, digamos, 1.5, será 1.5 ya sea en el sistema inglés o en SI o en cualquier otro sistema. En segundo lugar, nuestro análisis de unidades, este negocio de “análisis dimensional”, nos ha dicho que es más apropiado para entender lo que le sucede a un cuerpo en un flujo mirar el coeficiente de sustentación y el coeficiente de arrastre que mirar solo al levantamiento y arrastre.
1.13 “Parámetros de similitud”
Ahora bien, ¿qué pasa con los términos a la derecha? Nuestro análisis nos dice que estas agrupaciones de parámetros juegan un papel importante en la forma en que se producen los coeficientes de fuerza en un fluido. Veamos primero lo más simple, V/a.
V/a, por ahora, debería ser un término familiar para nosotros. Es la relación de la velocidad del cuerpo en el fluido a la velocidad del sonido en el fluido y se llama el Número Mach.
M = V/a.
Si estamos volando a la velocidad del sonido estamos en “Mach One” donde V = a. pero ¿qué tiene de magia Mach 1? Debe haber algo importante al respecto porque a mediados del siglo pasado los aerodinamistas estaban haciendo un gran problema al romper la barrera del sonido; es decir, ir más rápido que Mach 1. Para ver de qué se trataba y sigue siendo el alboroto veamos lo que sucede en un ala a medida que se acerca a la velocidad del sonido.
A medida que el aire se mueve sobre un ala acelera a velocidades superiores a la velocidad de “corriente libre”. Es decir, a una velocidad algo menor que la velocidad del sonido, la velocidad en la parte superior del ala puede haber alcanzado velocidades mayores que la velocidad del sonido. Esta aceleración a velocidad supersónica no causa ningún problema. Es ralentizar el flujo nuevamente lo que es problemático. Al flujo supersónico no le gusta disminuir la velocidad y muchas veces cuando lo hace lo hace de repente, a través de una “onda de choque”. Una onda de choque es una desaceleración repentina de un flujo de velocidad supersónica a subsónica con un aumento de presión acompañante (recuerde la ecuación de Bernoulli). Este cambio repentino de presión puede provocar fácilmente que el flujo sobre el ala se rompa o se separe, lo que resulta en una estela grande detrás del ala y un alto arrastre acompañante.
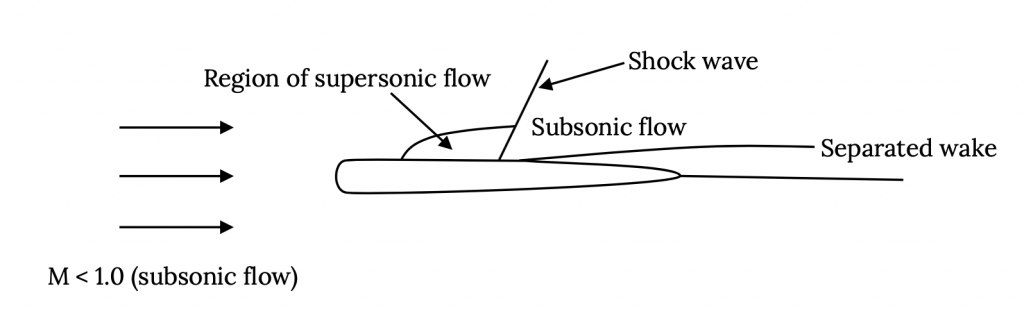
Entonces a cierta velocidad alta pero subsónica (número Mach) el flujo supersónico sobre el ala se ha desarrollado en la medida en que se forma un choque, y la resistencia aumenta debido a una estela separada y pérdidas a través del choque. El punto donde esto comienza a ocurrir se llama el número crítico de Mach, M crit . M crit será diferente para cada perfil aerodinámico y forma de ala. El resultado de todo esto es un comportamiento de coeficiente de arrastre algo así como el que se muestra en la gráfica a continuación:
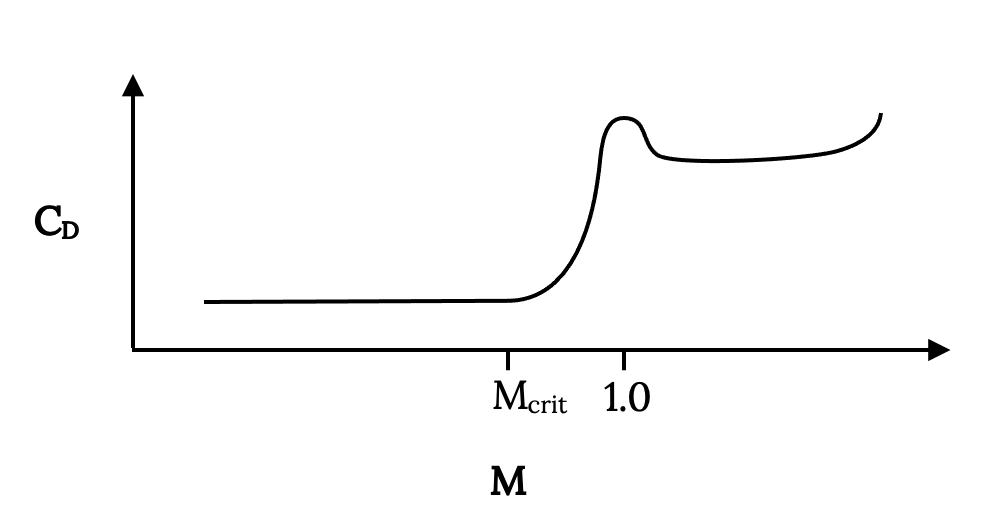
En realidad la teoría del flujo subsónico, compresible dice que la subida de arrastre que comienza en el número crítico de Mach sube asintóticamente en Mach 1; de ahí, el mito de la “barrera del sonido”. Desafortunadamente muchas personas, particularmente teóricos, parecían creer que la realidad tenía que encajar en su teoría más que a la inversa, y pensaban que el coeficiente de arrastre en realidad se volvió infinito en Mach 1. Tenían sus creencias reforzadas cuando algunos aviones de combate de alta potencia en la Segunda Guerra Mundial tuvieron fallas estructurales y de otro tipo a medida que se acercaban a la velocidad del sonido en inmersiones. Cuando la onda de choque causó la separación del flujo, cambió la forma en que el ala producía la elevación y la resistencia aerodinámica, a veces conduciendo a fallas estructurales en las alas y superficies de la cola que no estaban diseñadas para esas distribuciones de fuerzas. Esta separación de flujo también podría hacer inútiles las superficies de control en la cola y las alas o incluso hacer que “reviertan” su efectividad. El piloto se quedó con un avión que, si se mantenía unido estructuralmente, muchas veces se volvía imposible de controlar, lo que provocó un choque. En ocasiones, si el avión se mantenía unido y el piloto pudiera retener la conciencia, el número de Mach del avión disminuiría lo suficiente a medida que alcanzara menor altitud (la velocidad del sonido es función de la temperatura y es mayor a menor altitud) y el problema desaparecería, permitiendo que el piloto viva para decirle al historia.
En cualquier caso, los experimentalistas acudieron al rescate, señalando que las balas habían ido durante años más rápido que la velocidad del sonido (“nunca escucharás el disparo que te mata”) y diseñando un avión en forma de bala, el Bell X-1, con el empuje suficiente para llegar y pasar a Mach 1.

Una vez que el avión es realmente supersónico, en realidad hay dos choques en el ala, uno en el borde de ataque donde el flujo desacelera repentinamente de velocidad supersónica de transmisión libre a subsónica a medida que alcanza el punto de estancamiento, y otro en la parte trasera donde el flujo supersónico sobre el ala desacelera nuevamente. Como resultado, el “boom sónico” que se escucha desde un avión a velocidades supersónicas es realmente dos auges sucesivos en lugar de un solo golpe.
Por lo que es importante que seamos conscientes del número Mach de un flujo porque las fuerzas como el arrastre pueden cambiar drásticamente a medida que cambia el número de Mach. Ciertamente no queremos tratar de predecir las fuerzas en un avión supersónico a partir de los resultados de las pruebas a velocidades subsónicas o viceversa. Por otro lado, siempre y cuando todo lo que estamos considerando suceda por debajo del número crítico de Mach es posible que no tengamos que preocuparnos por estos “efectos de compresibilidad”. En general, por debajo de M crit podemos considerar que el flujo es “incompresible” y asumir que la densidad es una constante. Por encima de M crit no podemos hacer esto y debemos usar una forma compresible de ecuaciones como la ecuación de Bernoulli.
Con base en lo anterior, un nombre que a menudo le damos al número Mach es un “parámetro de similitud”. Los parámetros de similitud son cosas que debemos verificar para asegurarnos de que nuestras mediciones experimentales y cálculos tengan debidamente en cuenta cosas como la subida de arrastre que comienza en M crit. No queremos intentar predecir efectos de flujo compresible usando ecuaciones incompresibles o resultados de pruebas o viceversa.
Los otros tres términos de nuestra relación de fuerza son también parámetros de similitud. Veamos el primer término del lado derecho de esa relación. Esta agrupación de términos se conoce como el Número de Reynolds. El número de Reynolds puede verse en diferentes textos abreviados de diferentes maneras [Re, Rn, R, Re x, etc.] dependiendo de la convención en el ámbito de uso y de su aplicación. Aquí usaremos Re.
![Re= [ρVI] /μ](https://eng.libretexts.org/@api/deki/files/49070/a3d13778bf39a88d5b6785a4b9910556.png)
El número de Reynolds es realmente una relación de las fuerzas inerciales y las fuerzas viscosas en un fluido y es, de una manera muy real, una medida de la capacidad de un flujo para seguir una superficie sin separarse.
El número de Reynolds también es un indicador del comportamiento de un flujo en una región delgada junto a un cuerpo en un flujo donde las fuerzas viscosas son dominantes, determinando si ese flujo se comporta bien (laminar) o desordenado aleatoriamente (turbulento). Esta región delgada se llama capa límite.
Las fuerzas inerciales son aquellas fuerzas que hacen que un cuerpo o una molécula en un flujo continúen moviéndose a velocidad y dirección constantes. Las fuerzas viscosas son el resultado de colisiones entre moléculas en un flujo que obligan al flujo, al menos a escala microscópica, a cambiar de dirección. La combinación de estas fuerzas, como se refleja en el Número de Reynolds, puede llevar a que un flujo sea suave y ordenado y que se separe fácilmente de una superficie o sea aleatorio y turbulento y más probable que siga la curvatura de un cuerpo. También gobiernan la magnitud de fricción o arrastre viscoso entre un cuerpo y un flujo.
En general, una capa límite laminar, que ocurre en números Reynolds más bajos, da como resultado una baja fricción de arrastre (fricción de la piel) pero no es muy buena para resistir la separación y puede promover una gran resistencia de “estela” . Una capa límite turbulenta, que ocurre en números Reynolds más altos, tiene mayor resistencia a la fricción pero resiste mejor la separación del flujo, lo que lleva a una menor resistencia a la “estela”. Entonces, ¿cuál queremos? Todo esto depende de la forma del cuerpo y de las magnitudes relativas de estela y arrastre de fricción.
Un caso clásico para examinar es el flujo alrededor de un cilindro circular o, en tres dimensiones, sobre una esfera.
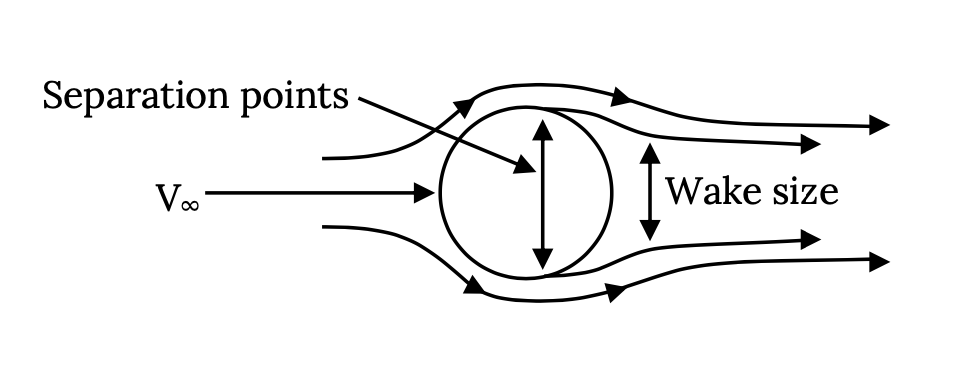
El flujo sobre un cilindro o esfera circular generalmente seguirá su superficie aproximadamente a la mitad del cuerpo y luego se romperá o se separará, dejando una “estela” de aire “muerto”. Esta estela causa mucho arrastre. Esta estela es similar a la que se ve cuando se conduce bajo la lluvia detrás de autos y sobre todo camiones grandes. En un camión el punto donde se separa el flujo es aproximadamente en las esquinas traseras de la carrocería del remolque o portón trasero. En un automóvil suele estar menos bien definido con la separación que ocurre en algún lugar entre la parte superior de la ventana trasera y la parte trasera del vehículo. En un automóvil aerodinámicamente bien diseñado el punto de separación estaría justo en la esquina de la cubierta trasera o en el “spoiler” si el automóvil tiene uno. Una estela pequeña da menor arrastre que una estela grande.
En un cilindro o esfera circular el punto de separación dependerá en gran medida del número de Reynolds del flujo. A valores más bajos de Re el flujo junto a la superficie corporal en la “capa límite tiende a ser “laminar”, un flujo que no es muy bueno para resistir la ruptura de la superficie o la separación. Menor Re generalmente resultará en una separación algo antes de que el flujo haya alcanzado el punto medio (90 grados) alrededor de la forma, dando una estela grande y un alto “arrastre de estela”. A mayor Re, el flujo en la capa límite tiende a ser turbulento y es capaz de resistir la separación, lo que resulta en una separación en algún punto más allá del punto medio y una menor resistencia a la estela y estela.
Debido a que el arrastre de estela es la forma predominante de arrastre en una forma como una esfera o cilindro circular, mucho mayor en magnitud que el arrastre de fricción, el punto de separación de flujo es el factor dominante para determinar el valor del coeficiente de arrastre del cuerpo.
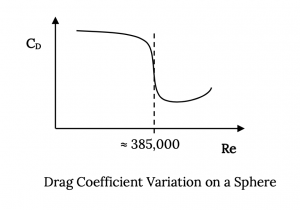
En la gráfica anterior el Número de Reynolds se basa en el diámetro de la esfera y el coeficiente de arrastre cae de un valor de aproximadamente 1.2 a aproximadamente 0.3 ya que el Número de Reynolds “crítico” se pasa a un valor de aproximadamente 385,000. Esta es una enorme disminución en el coeficiente de arrastre e ilustra cuán poderosa puede tener una influencia Re en un flujo y las fuerzas resultantes en un cuerpo.
Tenga en cuenta que un flujo alrededor de un cilindro o esfera podría caer en la porción de alto arrastre de la curva anterior debido a varias cosas ya que Re depende de la densidad, la velocidad, una longitud representativa y la viscosidad. La densidad y la viscosidad son propiedades de la atmósfera que, en la Troposfera, ambas disminuyen con la altitud. Las principales cosas que afectan a Re y al comportamiento del flujo a cualquier altitud dada serán la velocidad del flujo y la “longitud característica” o dimensión del cuerpo. La baja velocidad de flujo y/o una pequeña dimensión resultarán en un Re bajo y consecuentemente en un alto coeficiente de arrastre. Un alambre pequeño (un cilindro circular) tendrá un coeficiente de arrastre mucho mayor que un cilindro grande a una velocidad dada.
Por supuesto, el coeficiente de arrastre no es arrastre. El arrastre también depende del área proyectada del cuerpo, la densidad del aire y el cuadrado de la velocidad:
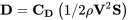
De ahí que no se pueda afirmar en general que una esfera pequeña tendrá más arrastre que una grande porque el arrastre dependerá de la velocidad al cuadrado y del área así como del valor del coeficiente de arrastre. Por otro lado, muchos objetos comunes de forma esférica desafiarán nuestra intuición en su comportamiento de arrastre debido a este fenómeno. Una bola de boliche colocada en un túnel de viento exhibirá una disminución pronunciada en el arrastre a medida que aumente la velocidad del túnel y se pase un Número de Reynolds alrededor de 385,000. Una esfera del tamaño de una pelota de golf o una pelota de béisbol estará en un número de Reynolds subcrítico incluso a velocidades superiores a 100 mph. Esta es la razón por la que cubrimos las pelotas de golf con “hoyuelos” y a los lanzadores de béisbol les gusta rozar pelotas de béisbol antes de tirarlas. Tener una superficie rugosa puede hacer que el flujo de la capa límite sea turbulento incluso en números de Reynolds donde el flujo normalmente sería laminar.
El comportamiento C D que se muestra en la gráfica anterior es para una esfera lisa o cilindro circular. La misma forma con una superficie rugosa experimentará una “transición” de un comportamiento de alto coeficiente de arrastre a valores más bajos de C D a números de Reynolds mucho más bajos. Una superficie rugosa crea su propia turbulencia en la capa límite que influye en la separación del flujo de la misma manera que la turbulencia “natural” que resulta de las fuerzas en el flujo que determinan el valor de Re. Los primeros golfistas, jugando con pelotas de golf suaves, probablemente descubrieron que, una vez que su pelota tenía algunas marcas o cortes, en realidad conducía más lejos. Probablemente entonces comenzaron a experimentar con patrones de ranura cortados en la superficie de las bolas. Esto llevó a los patrones de hoyuelos que vemos hoy en día que efectivamente bajan el arrastre de la pelota de golf (esto no es del todo bueno ya que los mismos hoyuelos empeoran el anzuelo o la rebanada de un golfista). Los puntos de sutura en una pelota de béisbol tienen el mismo efecto, y los lanzadores de béisbol han encontrado en sus propios experimentos algo poco científicos que rayar aún más la portada de una pelota nueva puede hacer que vaya más rápido así como escupir en ella puede hacer otras cosas extrañas.
La esfera o cilindro, como se mencionó anteriormente, es una forma clásica donde hay grandes efectos Re en el arrastre. Otras formas, particularmente formas “aerodinámicas” o de baja resistencia como perfiles aerodinámicos y alas, no exhibirán dependencias tan dramáticas de arrastre en Re, pero el efecto sigue ahí y debe considerarse.
Al igual que el número de Mach, Re se considera un parámetro de “similitud”, es decir, que queremos saber qué está pasando con cosas como el coeficiente de elevación y arrastre en un cuerpo debemos conocer su Número de Reynolds y saber de qué lado de cualquier Re “crítico” podríamos estar. El flujo sobre un ala podría ser bastante diferente a valores subcríticos de Re que a valores más altos, principalmente en términos de la ubicación de separación de flujo, pérdida y en la magnitud de la resistencia de fricción que depende de la extensión del flujo laminar y turbulento en la superficie del ala.
Entonces, al hacer cálculos y pruebas de túnel de viento necesitamos mirar la magnitud de Re y sus consecuencias. Al hacerlo, podemos adentrarnos en algunos dilemas reales cuando probamos modelos a escala en un túnel de viento. Si, por ejemplo, probamos un modelo a escala de una décima parte de un avión en un túnel de viento, nuestra “dimensión característica” en el Número de Reynolds será 1/10 de escala completa. Entonces, si queremos emparejar la prueba Re con la del plano a escala completa, uno de los otros términos debe cambiarse por un factor de diez. Cambiar la velocidad en un orden de magnitud a diez veces la velocidad de escala completa obviamente nos meterá en problemas con el otro parámetro de similitud, el número Mach, por lo que eso no servirá de nada. Debemos cambiar otra cosa o “engañar” usando rugosidad artificial para crear una capa límite turbulenta cuando el valor del número de Reynolds es realmente demasiado bajo para una capa límite turbulenta.
Uno de los mayores avances en aeronáutica se produjo en la década de 1920 cuando el Comité Asesor Nacional de Aeronáutica (NACA) en Langley Field, VA construyó lo que llamaron un “Túnel de Viento de Densidad Variable”. Esta fue una instalación de pruebas donde la densidad del aire podría incrementarse en un factor de 20, permitiendo la prueba de modelos a escala 1/20 a escala completa de Números Reynolds. El VDWT, ahora Monumento Histórico Nacional, era un túnel de viento subsónico construido dentro de una carcasa de acero presurizado en forma de huevo. Bastante sofisticado para su época, el túnel se presurizó a 20 atmósferas después de que se instaló el modelo de ala. El túnel fue operado y el modelo de prueba fue movido a través de un rango de ángulos de ataque de prueba por operadores que observaron sus pruebas a través de ventanas herméticas a presión que se asemejaban a ojos de buey de barco. Las alas modelo, cada una con una cuerda de cinco pulgadas y un tramo de treinta pulgadas, fueron mecanizadas a tolerancias muy ajustadas basadas en dimensiones elaboradas por científicos e ingenieros de NACA. Por primera vez el mundo de la aeronáutica contaba con mediciones aerodinámicas confiables y a gran escala de alas con una amplia gama de formas aerodinámicas.
Hoy en día, en las pruebas de túnel de viento generalmente “engañamos” al número de Reynolds usando “tiras de disparo”, pequeñas líneas similares a papel de lija colocadas cerca de los bordes de ataque de las alas y fuselajes para forzar el flujo a la transición de flujo laminar a flujo turbulento en ubicaciones calculadas antes de las pruebas. A pesar de que el Túnel de Viento de Densidad Variable se retiró hace mucho tiempo, todavía tenemos una capacidad única en lo que hoy es el Campo NASA-Langley con la Instalación Nacional Transónica, un túnel de viento en el que el gas de trabajo es nitrógeno a temperaturas muy cercanas a su punto de licuación. Dado que la densidad, la viscosidad y la velocidad del sonido cambian con la temperatura, es posible en la NTF simular números de Reynolds y números Mach a escala completa al mismo tiempo. Si bien las pruebas no son fáciles a estas bajas temperaturas, las investigaciones realizadas correctamente en la NTF pueden producir datos aerodinámicos que no se pueden obtener de ninguna otra manera.
Al concluir esta discusión del Número de Reynolds cabe señalar que la “longitud característica” en Re puede tomar varios valores diferentes dependiendo de la convención y que el valor de Re en el que ocurre la transición de flujo laminar a flujo turbulento también puede variar con la aplicación. Como se mostró anteriormente, basamos el Número Reynolds para un cilindro o esfera circular en su diámetro. La transición Re es poco menos de 400,000. Sin embargo, si fuéramos ingenieros mecánicos o civiles trabajando con flujos a través de tuberías, usaríamos el diámetro de la tubería como nuestra dimensión y encontraríamos que la transición tiene lugar en Re de aproximadamente 5000, unos dos órdenes de magnitud diferentes a la transición en la esfera. Tenemos que ser conscientes de esta perspectiva diferente sobre las magnitudes importantes de Re al platicar con nuestros amigos en otros campos sobre flujos.
Cuando hablamos del valor del Número de Reynolds en un ala o un avión, la dimensión característica utilizada es la cuerda media o promedio del ala, la distancia promedio desde el borde delantero hasta el borde de salida del ala. Cuando estamos haciendo cálculos detallados sobre el comportamiento del flujo en la capa límite usaremos otra dimensión más, la distancia desde el punto de estancamiento sobre la superficie del cuerpo hasta el punto donde estamos haciendo los cálculos.
Bien, hemos encontrado nuestro algo sobre la importancia de Mach Number y Reynolds Number, ¿qué pasa con las otras dos agrupaciones de parámetros en la ecuación de dependencia de fuerza que teníamos antes?
Hubo otros dos términos, Gl/v 2, y P/ρ V. El primero de ellos es una relación de fuerzas gravitacionales e inerciales y se relaciona con fuerzas que surgen como consecuencia de que un cuerpo está cerca de una “interfaz” como el suelo o la superficie del océano. Este término suele ser invertido y su raíz cuadrada se conoce como el Número Froude.
Número de Froude = V/[gl] 1/2,
donde la longitud en la ecuación es la distancia entre el cuerpo y la interfaz de fluido; es decir, la altura del avión por encima de la pista o la profundidad de un submarino debajo de la superficie. A menos que esa distancia sea menor que aproximadamente el doble del diámetro del submarino o la cuerda del ala, el Número de Froude generalmente puede ignorarse; pero dentro de este rango, puede ayudar a explicar los aumentos en la resistencia o elevación que pueden ocurrir cuando un cuerpo está cerca de una superficie.
El término final, el Número Euler, P/ ρ V, realmente no es importante en el aire, sino que se usa cuando se busca la probabilidad de efectos de cavitación en un cuerpo en el agua. Cuando la presión en el agua se baja al punto de vapor del agua a una temperatura dada, el agua hervirá aunque la temperatura sea inferior a su punto de ebullición habitual. Cuando el flujo se acelera alrededor de una hélice o casco de barco, la presión puede llegar a ser lo suficientemente baja localmente como para hervir el agua, y esta ebullición o cavitación puede causar serios aumentos en la resistencia, el ruido, la pérdida de empuje de la hélice y daños a la superficie misma. El término utilizado para examinar esto es una modificación del encontrado en nuestro análisis, reescrito ligeramente para dar cuenta de la importancia de la presión de vapor.
![Número de cavitación (σ) = [P−Pv] /ρv2](https://eng.libretexts.org/@api/deki/files/49074/3dd47505e130d911aee173a47327ad76.png)
Tenga en cuenta que el denominador es una agrupación familiar de parámetros, el doble de la presión dinámica.
1.14 perfiles aerodinámicos y sus coeficientes aerodinámicos
Al principio de este texto, analizamos la terminología que se utiliza para definir la forma del perfil aerodinámico, cosas como acorde, curvatura y grosor, así como las cosas como span, acorde, barrido y relación de aspecto que definen la forma de un ala completa. En la sección anterior encontramos que la mejor manera de hablar de las fuerzas que actúan sobre un perfil aerodinámico (2-D) o un ala (3-D) es en términos de coeficientes no dimensionales. Volvamos a echar un vistazo a esos coeficientes y cómo se definen tanto en dos como en tres dimensiones y veamos la forma en que estos cambian en función del ángulo de ataque del ala o superficie aerodinámica al flujo.
Unas pocas páginas atrás definimos los coeficientes de elevación y arrastre para un ala. Estos se repiten a continuación y se extienden para definir un coeficiente de momento de cabeceo:
Obsérvese nuevamente que el área “S” es el área “planform” del ala, el área “proyectada” que uno vería mirando hacia abajo sobre el ala y no su superficie real. El coeficiente de momento tiene un denominador ligeramente diferente que incluye la cuerda media o promedio junto con el área de forma plana para hacer que el coeficiente no tenga unidades, ya que el momento de cabeceo tiene unidades de fuerza por distancia. Un poco más tarde veremos el momento con más detalle y veremos qué punto (s) de referencia deben utilizarse para medir o calcular ese momento.
Los coeficientes anteriores están en forma tridimensional y son como los definiríamos para un ala completa. Si solo estamos mirando la sección aerodinámica, una porción bidimensional del ala, el área en el denominador simplemente se convertiría en el acorde.
Sería útil saber algo sobre los rangos típicos de estos coeficientes en dos o tres dimensiones así tendremos alguna idea de cuán válidos pueden ser nuestros cálculos.
-2.0 < C L < +2.0 para un ala o superficie aerodinámica normal sin flaps
-3 .0 < C L < +3 .0 para un ala o superficie aerodinámica con solapas
0.005 < C D < 0.025 para un ala o superficie aerodinámica (más para todo un avión)
-0.1 < C M < 0.0 para un ala o superficie aerodinámica cuando se mide a c/4
También hay que señalar que el momento de pitcheo se define como positivo cuando es “nariz arriba”. Dependiendo de la dirección de la superficie aerodinámica o del ala dentro de un sistema de ejes, esto puede ser contrario a la costumbre matemática. De hecho, la mayoría de los textos suelen tratar los problemas aerodinámicos como si la velocidad de transmisión libre viniera de la izquierda en la dirección x positiva y el ala o superficie aerodinámica estuviera mirando hacia la izquierda en una dirección x negativa. En tal representación, un momento de pitcheo positivo sería en el sentido de las agujas del reloj aunque el tratamiento matemático habitual le asignaría un signo negativo.
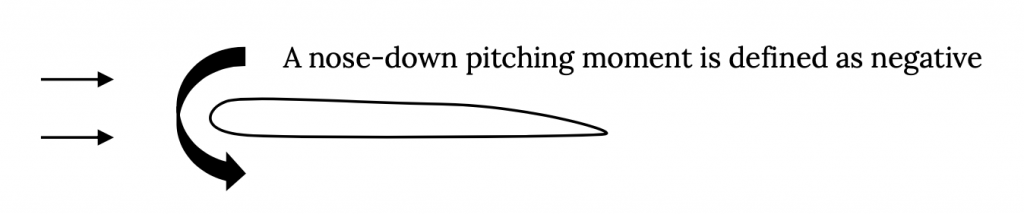
1.15 Ángulo de ataque
También necesitamos definir la forma en que relacionamos la orientación del ala con el flujo; es decir, el ángulo de ataque del ala o perfil aerodinámico, α. Al mismo tiempo podemos mirar la definición para la dirección de elevación y arrastre.
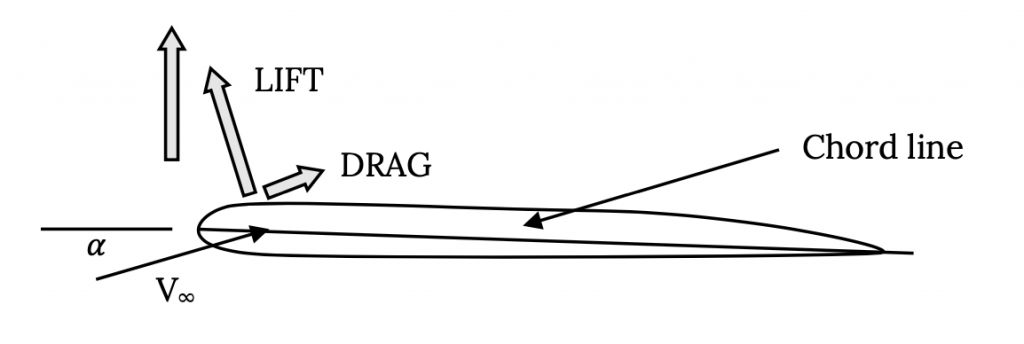
Tenga en cuenta que el ángulo de ataque, α, se define como el ángulo entre el ala o cuerda aerodinámica y el vector de velocidad de transmisión libre, no entre la velocidad y la horizontal. También tenga en cuenta que Lift y Drag se definen como perpendiculares y paralelas, respectivamente, al vector de velocidad de transmisión libre, no “arriba y atrás” o perpendicular y paralela a la cuerda. Estas definiciones suelen requerir cuidados porque no siempre son intuitivas. En muchas situaciones la fuerza que definimos como elevación tendrá un componente “hacia adelante” a lo largo de la línea de cuerda del ala. Esta es, de hecho, la razón por la que las palas del rotor de helicóptero y girocóptero pueden girar sin energía en lo que se conoce como el modo de “autorrotación”, dando sustentación con un rotor sin alimentación.
Dadas estas definiciones, veamos la forma en que el coeficiente de elevación y arrastre suele cambiar con el ángulo de ataque.
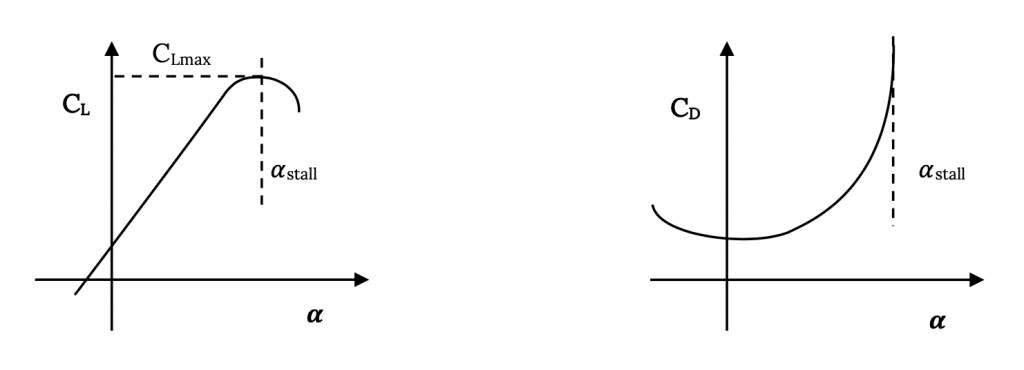
Veamos algunas cosas en las parcelas anteriores:
-
- El coeficiente de sustentación varía linealmente con el ángulo de ataque hasta que el ala se acerca a la parada. La parada comienza cuando el flujo comienza a desprenderse o separarse de la superficie superior del ala y puede progresar rápida o gradualmente sobre la superficie.
- Cuando el coeficiente de sustentación ya no aumenta con el ángulo de ataque, en medio de la progresión de la calada, tenemos C Lmax el mayor valor de coeficiente de sustentación que podemos obtener para un perfil aerodinámico o ala en particular en un número de Reynolds dado. El valor de C Lmax, en general, aumentará con el aumento de Re.
- El coeficiente de sustentación no se muestra como cero en valor en un ángulo de ataque cero. En una superficie aerodinámica “simétrica”; es decir, una sin combadura, la elevación será cero en ángulo de ataque cero. En una superficie aerodinámica combada la elevación será cero en algún ángulo de ataque negativo que llamamos el “ángulo de ataque de elevación cero”, α L0.
- El arrastre aumenta rápidamente en el puesto.
Deberíamos explorar más a fondo esta idea de puesto porque algo parece mal aquí. La trama anterior muestra que el puesto es donde tenemos nuestro coeficiente de elevación máximo. ¿Cómo puede ser eso cierto cuando siempre nos han dicho que el puesto es donde un avión pierde sustentación?
Nuestro dilema se deriva de los significados de dos términos diferentes, elevación y coeficiente de elevación. Veamos la relación entre la elevación y el coeficiente de elevación.
Elevación = CL [1/2 ρ V2S]
Para tener elevación debemos tener dos cosas, un buen coeficiente de sustentación y la velocidad necesaria para convertir ese coeficiente de sustentación en elevación. Entonces, ¿cuál es el problema aquí? El problema es el arrastre.
Cuando un avión alcanza C Lmax, tiene su mayor capacidad de elevación o coeficiente de elevación posible. Pero mirando la otra trama, la de coeficiente de arrastre, vemos que también tiene un coeficiente de arrastre que aumenta rápidamente. El arrastre resultante provoca una reducción en la velocidad y, dado que la velocidad es cuadrada en la relación anterior, tiene una influencia mucho más poderosa en la elevación que el coeficiente de sustentación. La elevación disminuye a medida que baja la velocidad y, de hecho, a pesar de que tenemos un coeficiente de elevación muy alto no podemos hacer suficiente elevación para superar el peso del avión. Y, como podemos ver en la trama de la izquierda, si vamos más allá del ángulo de ataque de parada también obtenemos una disminución en el coeficiente de sustentación.
Como se señaló anteriormente hasta la calada, se muestra que el coeficiente de sustentación varía linealmente con el ángulo de ataque y se convierte en cero en el ángulo de ataque de elevación cero L0. Ante esto podemos escribir una ecuación simple para el valor de CL.
La teoría mostrará y el experimento verificará que para una sección aerodinámica (un corte bidimensional de un ala) esta pendiente, dC L/d α, es igual a 2 π , donde los ángulos de ataque son expresado en radianes. Entonces, teóricamente para una sección de superficie aerodinámica, esta ecuación se convierte en:
![CL=2π [α−αL0] CL=2π [α−αL0]](https://eng.libretexts.org/@api/deki/files/49085/b32694dc3cfa9c46969bb541597b89a8.png)
Para un ala tridimensional la pendiente de la curva puede ser menor y tanto la teoría como el experimento pueden ser utilizados para determinar esa pendiente 3-D.
Entonces, ¿cómo influye la forma de la sección aerodinámica en esta relación? Primero, la forma de la línea de curvatura determinará el valor del ángulo de ataque de elevación cero. Encontraremos en un curso posterior en aerodinámica que hay formas de calcular L0 a partir de la forma de la línea de comba aerodinámica.
Es más difícil e incluso puede ser imposible calcular el valor de C Lmax y el ángulo de ataque para el calado. Estas son funciones del grosor del perfil aerodinámico y la forma de su superficie así como de cosas como el Número de Reynolds. Tenemos que mirar los efectos de fricción y la teoría de la capa límite para incluso comenzar a tratar con éxito la región de estancamiento. Nuestra única alternativa es utilizar pruebas de túnel de viento. Y esto es lo que hicieron las personas del Comité Consultivo Nacional de Aeronáutica (NACA) que se mencionó anteriormente en su Túnel de Viento de Densidad Variable.
1.16 Perfil aerodinámico NACA
En la década de 1920, los científicos e ingenieros de la NACA se propusieron por primera vez examinar sistemáticamente cómo cosas como la forma de la línea de curvatura y las distribuciones de espesor influyeron en el comportamiento de los perfiles aerodinámicos. Comenzaron su búsqueda al decidir cómo definir una forma de perfil aerodinámico usando solo tres números y cuatro dígitos. Observaron las mejores formas de perfil aerodinámico de su tiempo y encontraron una buena manera de variar el grosor del perfil aerodinámico desde su borde de ataque hasta el borde de salida y escribieron una ecuación para esta distribución que permitió que todo se definiera en términos de un número de uno, dos dígitos. Después escribieron dos ecuaciones para la línea de curvatura aerodinámica, una para la parte delantera del ala hasta el punto de máxima curvatura y la otra para la parte de popa del ala detrás de la ubicación de máxima curvatura. Estas dos ecuaciones dependían de dos números de un solo dígito, uno dando la ubicación del punto máximo de curvatura en décimas de la cuerda y la otra dando la distancia máxima entre las líneas de curvatura y cuerda en centésimas de la cuerda. Después utilizaron estos cuatro dígitos para identificar el perfil aerodinámico resultante.
Por ejemplo, el perfil aerodinámico NACA 2412 es un perfil aerodinámico donde cada uno de los números significa algo sobre la forma:
2 — La distancia máxima entre la cuerda y las líneas de curvatura es del 2% de la cuerda.
4 — La ubicación del punto de máxima inclinación se encuentra en el 40% de cuerda.
12 — El grosor máximo del perfil aerodinámico es del 12% de la cuerda.
Estos cuatro dígitos (tres números) podrían usarse con ecuaciones relacionadas para dibujar la forma del perfil aerodinámico.
Usando este método, la NACA podría observar sistemáticamente los efectos de solo la cantidad de curvatura máxima probando una serie de formas como 1412, 2412, 3412, etc., o podrían mantener estable la curvatura máxima y observar el efecto de colocación de la curvatura máxima (2212, 2312, 2412, 2512, etc.), o fijar el forma de la línea de inclinación y observar el efecto de variación de espesor (0006, 0009, 0012, 0015, 0021, etc.). Tenga en cuenta que este último conjunto de perfiles aerodinámicos son todos simétricos; es decir, inclinación cero. Y esto es precisamente lo que se hizo con pruebas en cientos de perfiles aerodinámicos. Se probó una amplia variedad de perfiles aerodinámicos en el Túnel de Viento de Densidad Variable y se graficaron los resultados. Las parcelas de muestra se presentan en el Apéndice A.
El primer conjunto, Figuras A-1 (A&B), es para una sección de perfil aerodinámico NACA 0012. Tenga en cuenta que esta es una sección simétrica de superficie aerodinámica (el primer cero indica que no hay comba y por lo tanto el segundo número no tiene sentido) y tiene un grosor del 12%. Primero vemos que hay varias parcelas en cada una de las dos gráficas y que existen múltiples definiciones del eje vertical para cada parcela. En la gráfica de la izquierda el eje horizontal es el ángulo de ataque dado en grados y el eje vertical primario es el coeficiente de elevación de sección o bidimensional. También hay un eje vertical secundario para el coeficiente de momento de cabeceo (con el momento medido con relación a c/4, la cuerda de cuarto).
Se da mucha información en la parcela A. Lo primero que notamos es que hay dos conjuntos de curvas de coeficiente de sustentación y que cada una de estas parece tener un par de parcelas diferentes de la región de la parada. Tenga en cuenta que la porción lineal de un conjunto de estas curvas pasa por el eje de la gráfica mostrando que el coeficiente de sustentación es cero en un ángulo de ataque de cero. Estas curvas son para el perfil aerodinámico básico 0012 que es un perfil aerodinámico simétrico y no tendrá loft en ángulo de ataque cero.
Existen, como se señaló anteriormente, al menos dos parcelas de región de calado diferentes para esta superficie de sustentación simétrica. Para entender estos necesitamos mirar la información de inserción sobre el número de Reynolds (anotado como simplemente “R” en estas parcelas). Hay cuatro símbolos diferentes que se muestran en este recuadro. El símbolo “diamante” denotó datos para el ala probada en un número de Reynolds de 9 x 10 6, el cuadrado para Re = 6 x 10 6 y el círculo para Re = 3 x 10 6. El otro símbolo, un triángulo, es para el perfil aerodinámico probado con una “rugosidad estándar” o una superficie rugosa a un Re = 6 x 10 6. Por lo general, cuanto mayor sea el valor del número de Reynolds, mayor será el valor del coeficiente de elevación máximo pero en este caso particular solo hay un ligero aumento con C Lmax moviéndose hacia arriba de aproximadamente 1.5 a 1.6 a medida que el número de Reynolds en el perfil aerodinámico liso aumenta de 3 a 6 x 10 6. Para la superficie lisa, el estancamiento siempre ocurre en un ángulo de ataque de 16 grados. Tenga en cuenta también que el perfil aerodinámico también se detiene a menos 16 grados de ángulo de ataque, verificando su comportamiento simétrico. La superficie rugosa provoca un calado mucho más temprano y menor valor de C Lmax.
Entonces, ¿cuál es el otro conjunto de “curvas de elevación” que se desplazan hacia arriba y hacia la izquierda en esta parcela? Estos son los datos para el perfil aerodinámico 0012 con un flap de borde de salida. Otra información de inserción en la trama nos dice que se trata de un flap dividido con un acorde del 20% del acorde aerodinámico y se desvía 60 grados. Tenga en cuenta que el perfil aerodinámico básico se dibuja a escala en la gráfica de la derecha y el flap y su deflexión se anotan en líneas discontinuas en el dibujo.
Estos datos muestran que para este flap en particular la curva de sustentación se desplaza hacia la izquierda de tal manera que tiene sustentación cero a menos 12 grados, es decir α LO, el ángulo de ataque de elevación cero, es menos 12 grados para el perfil aerodinámico aleteado. Las curvas muestran que la deflexión del colgajo ha aumentado C Lmax de aproximadamente 1.6 hasta aproximadamente 2.4, un incremento del 50%. C Lmax para el perfil aerodinámico de superficie rugosa ha pasado de 1.0 a 1.9.
Ahora, hay otras dos curvas en esta parcela. Son curvas para el coeficiente de momento de cabeceo alrededor del cuarto de cuerda, con y sin desviación de flap. Primero tenga en cuenta que la escala a la izquierda de la parcela es diferente para el coeficiente de momento que para el coeficiente de elevación. No confundas estas dos escamas. A continuación, tenga en cuenta que la parte superior de estas dos curvas es para el ala sin flaps y que tiene un valor de cero sobre el rango de ángulo de ataque donde la curva de sustentación es lineal. Esto significa que el momento de pitcheo es cero en el acorde de cuarto para este perfil aerodinámico. Esto es cierto para todos los aeroplanos simétricos. Definimos el lugar donde el momento de cabeceo es cero como el centro de presión (a veces llamado centro de elevación) y definimos el lugar donde el coeficiente de momento de cabeceo es constante con ángulo de ataque cambiante como centro aerodinámico. Los veremos más a fondo un poco más tarde. Para una superficie aerodinámica simétrica, el centro de presión y el centro aerodinámico están ambos en c/4.
Ahora veamos la trama B para el perfil aerodinámico 0012. Esta gráfica muestra los resultados de las pruebas para el coeficiente de arrastre y el coeficiente de momento y los grafica versus el coeficiente de sustentación, no el ángulo de ataque. Entonces, para encontrar el coeficiente de arrastre en un cierto ángulo de ataque requiere que primero encontremos el valor de C L en ese ángulo de ataque y luego lo utilicemos para encontrar C D.
Nuevamente en esta parcela hay diferentes conjuntos de datos para diferentes valores de número de Reynolds y rugosidad. Tenga en cuenta que C D es el más pequeño en ángulo de ataque cero para este perfil aerodinámico simétrico como se esperaría, y que a medida que aumenta el ángulo de ataque, C D aumenta. La curva de momento en esta parcela es para el coeficiente de momento en el centro aerodinámico y no para c/4 como en la parcela de la izquierda. Sin embargo, como se señaló anteriormente, para una superficie aerodinámica simétrica el centro aerodinámico está en el cuarto de cuerda por lo que estos son los mismos aquí.
La siguiente gráfica del Apéndice A, Figura A-2 (A&B), muestra datos similares para el perfil aerodinámico NACA 2412. Al igual que el perfil aerodinámico 0012 esta forma tiene 12% de grosor pero ahora tiene una ligera curvatura (uno por ciento) con la curvatura máxima ubicada en 40% de la cuerda. Así podemos comparar estas parcelas con las primeras para ver el efecto de comba añadida. Al observar todas las mismas cosas mencionadas anteriormente vemos que el perfil aerodinámico tiene ahora un coeficiente de sustentación positivo (0.15) en ángulo de ataque cero y que el ángulo de ataque de elevación cero es ahora de menos un grado. C Lmax sigue siendo alrededor de 1.6 para el ala sin aletear pero con la desviación del flap ha aumentado ligeramente desde el caso simétrico. El coeficiente de momento de pitcheo ya no es cero a c/4 sino que sigue siendo constante, ahora a un valor de aproximadamente — 0.025; es decir, un momento de pitcheo ligeramente hacia abajo. Dado que el momento de pitcheo en c/4 sigue siendo constante este punto sigue siendo el centro aerodinámico pero ya no es el centro de presión. El coeficiente mínimo de arrastre es aproximadamente el mismo que para el ala simétrica y sigue siendo mínimo en un ángulo de ataque aproximadamente cero pero este ya no es con coeficiente de sustentación cero.
Podemos ver el resultado de mayores incrementos en la curvatura al dos por ciento en las parcelas para el perfil aerodinámico NACA 2412. No hay datos de desviación de colgajo incluidos en estas parcelas. En esta trama podemos ver que el momento de pitcheo sigue aumentando negativamente (nariz hacia abajo) a medida que se incrementa la comba y que el coeficiente mínimo de arrastre también ha comenzado a aumentar. Se ve que el ángulo de ataque de elevación cero y la elevación en ángulo de ataque cero continúan aumentando en magnitud a medida que se agrega la inclinación como sugiere la teoría.
Las siguientes gráficas, Figura A-3 (A&B), para el NACA 2415 muestran cambios muy leves en el comportamiento del perfil aerodinámico con aumento de grosor de 12% a 15% pero para la sección NACA 2421 vemos que el grosor agregado está dando como resultado una pérdida más temprana, disminución de C Lmax, aumento del coeficiente de arrastre, y en una variación del coeficiente de momento no lineal con ángulo de ataque alrededor del cuarto de cuerda. Esto podría sugerirnos que el 21% de grosor es un poco demasiado grueso.
Los datos (Figura A-4 (A&B), para el perfil aerodinámico NACA 4412 continúan ilustrando las tendencias discutidas anteriormente, observando el efecto de agregar más combadura.
Los dos últimos conjuntos de parcelas, Figuras A-5 y A-6, son para un diseño diferente de superficie aerodinámica, el perfil aerodinámico de la serie NACA 6, una forma que discutiremos primero antes de profundizar en las gráficas.
El NACA probó una amplia variedad de formas de superficie aerodinámica en sus investigaciones de cuatro dígitos en series. Sin embargo, había algunos límites a las variaciones de forma que se podían obtener usando la designación de cuatro dígitos. No pudieron, por ejemplo, mirar un perfil aerodinámico con comba máxima al 25% del acorde, solo 20% o 30%. De ahí que pasaron a desarrollar una serie de perfil aerodinámico de 5 dígitos. Posteriormente observaron una serie aerodinámica diseñada para optimizar el uso del flujo laminar y turbulento en la capa límite para minimizar la resistencia aerodinámica y desarrollaron los perfiles aerodinámicos de la serie 6. Echemos un vistazo a ambos.
La serie NACA de 5 dígitos utilizó la misma distribución de espesor que la serie de cuatro dígitos, pero permitió una mayor flexibilidad en la definición de la posición de curvatura máxima. También se intentó relacionar la cantidad de curvatura y el primer dígito en la designación de perfil aerodinámico con un “diseño C L”. El diseño C L es el coeficiente de sustentación visto como óptimo para los objetivos de rendimiento de un avión determinado. Un transporte de largo alcance puede tener un coeficiente de sustentación de diseño de alrededor de 0.3, mientras que un avión de combate podría tener un diseño C L más alto. A continuación se da un ejemplo de un perfil aerodinámico de 5 dígitos NACA con una explicación del sistema de numeración:
NACA 23021
2 — la curvatura máxima es aproximadamente 0.02 y el diseño C L es 2 x 0.15 = 3.0
30 — la posición de la inclinación máxima es (0.30/2) veces la cuerda o 0.15c
21 — el grosor máximo es 0.21c
La serie NACA 6 (tenga en cuenta que esto se llama simplemente la serie “seis” y no la serie de seis dígitos aunque la mayoría de los números de designación tienen seis dígitos) se desarrolló en la década de 1930 en un intento de diseñar una serie de formas de perfil aerodinámico que optimizaran las áreas de flujo laminar y turbulento en el capa límite en el ala. Como comentamos anteriormente, el flujo laminar en la capa límite es un flujo de baja fricción y eso es bueno; sin embargo, el flujo laminar es pobre para resistir la separación del flujo y la separación da como resultado un alto arrastre y baja sustentación. Una capa límite turbulenta es mucho mejor para resistir la separación de flujo que una laminar, pero tiene mayor resistencia a la fricción.
La separación del flujo es mucho más probable cuando el flujo está desacelerando (donde la presión está aumentando, conocido como gradiente de presión “adverso” porque la separación es probable). El flujo sobre una superficie aerodinámica generalmente se acelerará sobre el frente de la forma hasta el punto de su presión mínima que generalmente nos encontramos en aproximadamente el punto de espesor máximo. Aquí es seguro tener flujo laminar porque no es probable que el flujo intente separarse. Si queremos más flujo laminar y, de ahí, una mayor parte del perfil aerodinámico con baja fricción, podemos mover el punto de espesor máximo más hacia la parte trasera del perfil aerodinámico. La idea es obtener lo más grande posible un área de flujo laminar y luego dejar que la capa límite pase a flujo turbulento antes de que el grosor comience a disminuir para que la capa límite turbulenta resista la separación. Esto da como resultado un perfil aerodinámico con un radio de borde de ataque más pequeño que los diseños más antiguos y con el grosor máximo más atrás.
Dos de estas formas de la serie 6 se esbozan como parte de sus gráficos de datos NACA en el Apéndice A, los perfiles aerodinámicos NACA 65 1-212 y 65 1 -412. Una cosa que es inmediatamente obvia al comparar estas dos gráficas de datos con las de los datos de perfil aerodinámico de 4 dígitos de NACA es el “bucket” en el centro de las curvas de coeficiente de arrastre en las gráficas de la derecha. Este llamado “cubo de arrastre” es característico de los perfiles aerodinámicos de la serie 6. Todos estos perfiles aerodinámicos tienen una región de ángulo de ataque o coeficiente de sustentación sobre la cual el arrastre es considerablemente menor que en otros ángulos de ataque. Este es el rango de ángulo de ataque donde el flujo laminar puede existir sobre una gran parte de la porción delantera del perfil aerodinámico, dando una reducción en la resistencia de fricción.
El sistema de numeración de perfil aerodinámico de la serie 6 está diseñado para ayudar al diseñador/aerodinamista a seleccionar el mejor perfil aerodinámico para el trabajo, indicando dónde se encuentra el centro del “cucharón de arrastre” y indicando la extensión (ancho) de ese cucharón de arrastre. En otras palabras, si un diseñador quiere un ala con una sección aerodinámica que dé un coeficiente de sustentación de diseño de 0.2 él o ella quiere que el centro de la cubeta de arrastre esté en una C L de 0.2 por lo que el avión podrá hacer su misión de diseño en las condiciones de arrastre más bajas posibles. De ahí que uno de los números en la designación de la serie 6 indica a la C L para el centro del cucharón de arrastre. Veamos una de estas designaciones de perfil aerodinámico y veamos qué significan los números.
NACA 65 1 -212
6 — esta es meramente la designación de “serie”
5 — la ubicación de presión mínima en elevación cero está en cuerda del 50%
1 — se trata de un subíndice que puede aparecer o no en una designación de 6 series. Significa que el ancho del “cucharón de arrastre” se extiende por un rango de C L de 0.1 por encima y por debajo del diseño C L
2 — el diseño C L es 0.2
12 — como siempre, el grosor máximo como cuerda%
Ahora bien, si volvemos a mirar los datos para el perfil aerodinámico anterior vemos que el cucharón de arrastre está efectivamente centrado en un coeficiente de sustentación de aproximadamente 0.2 y el cucharón se extiende por al menos un rango de C L de 0.1 a ambos lados de su centro. De igual manera si miramos las parcelas para el NACA 65 1 -412 encontramos que la cubeta de arrastre está más a la derecha y centrada aproximadamente a una C L de 0.4.
Una comparación más cercana de estos datos aerodinámicos de la serie 6 con los de los casos de la serie de 4 dígitos mostrará que no todo es mejor. Los perfiles aerodinámicos de la serie 6 a menudo se detienen un poco antes debido a sus radios de borde de ataque más pequeños y, por lo tanto, tienen valores C Lmax ligeramente más bajos que sus homólogos anteriores. También sus coeficientes de arrastre fuera del rango del cucharón de arrastre pueden ser más altos que los perfiles aerodinámicos convencionales. Como en todas las cosas en la vida real, las mejoras en un área suelen ir acompañadas de penalizaciones en otras. Sin embargo, los perfiles aerodinámicos de la serie 6 son excelentes diseños y todavía se utilizan hoy en día en muchos aviones.
1.17 Momento de pitcheo
Antes de profundizar en el desarrollo del perfil aerodinámico debemos dar un paso atrás y mirar más a fondo dos cosas mencionadas anteriormente, el centro aerodinámico y el centro de presión. Estos son dos puntos importantes en el perfil aerodinámico que dependen del comportamiento del momento de pitcheo. Un momento debe ser referenciado a un punto y estos resultan ser puntos muy significativos sobre los que hacer referencia al momento de pitcheo en una superficie aerodinámica o ala.
El momento en una superficie aerodinámica está relacionado principalmente con la forma en que se produce la elevación en la forma. El arrastre también contribuye al momento pero en menor medida. A velocidades subsónicas, la elevación en la mayoría de los perfiles aerodinámicos es mayor en la parte delantera de la forma que en la parte trasera y podría verse así:
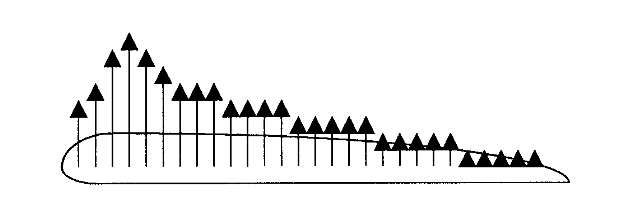
Si elegimos hablar del momento de pitcheo sobre el borde de ataque del perfil aerodinámico, el momento siempre sería nariz abajo o en sentido contrario a las agujas del reloj. Si resumimos los momentos en algún momento aproximadamente a la mitad de camino hacia atrás a lo largo del acorde el momento sería la nariz hacia arriba o hacia la derecha ya que las fuerzas de elevación a la izquierda son mayores que las de la derecha. Obviamente hay algún punto entre el borde de ataque del perfil aerodinámico y su centro donde los momentos sumarían a cero. Este sería el centro de presión. Podría ser interesante y útil saber dónde está este lugar ya que parece ser un punto de equilibrio natural o especie. El único problema es que esta posición puede moverse a medida que el perfil aerodinámico cambia de ángulo de ataque. Por ejemplo, a mayor ángulo de ataque se podría producir aún más sustentación cerca de la parte frontal de la superficie aerodinámica y el centro de presión se movería más cerca de la nariz del perfil aerodinámico.
Resulta que, de acuerdo con la teoría aerodinámica que examinarás en un curso posterior, hay otro punto que es de aún más interés, el centro aerodinámico. Este es el punto donde el coeficiente de momento (no el momento en sí) es constante en un amplio rango de ángulo de ataque. La teoría aerodinámica básica nos dirá que esto es aproximadamente en el cuarto de cuerda del perfil aerodinámico en flujo subsónico. Este fue el caso de los perfiles aerodinámicos cuyos datos se muestran en el Apéndice A.
La teoría también mostrará y el experimento verificará que para una superficie aerodinámica simétrica como la forma NACA 0012 en el Apéndice A el centro aerodinámico y el centro de presión están en el mismo lugar. Es decir, para perfiles aerodinámicos simétricos en el centro aerodinámico el momento de cabeceo no solo es constante sino que también es cero. Esto hace que el centro aerodinámico sea un lugar muy conveniente para ubicar los principales elementos estructurales o para usar como punto de equilibrio para superficies de control.
1.18 Camber y flaps, y Vuelo a Velocidades Reducidas
Hemos visto en los datos del Apéndice A que a medida que aumenta la curvatura de un ala cambia su rendimiento aerodinámico. Al observar los datos de los perfiles aerodinámicos NACA 0012, 1412 y 2412 vimos que a medida que se incrementa la curvatura (indicada por el primer término en el sistema de numeración de cuatro dígitos NACA) la curva de elevación se desplaza hacia la izquierda dando más coeficiente de sustentación en ángulo de ataque cero, un ángulo de ataque cada vez más negativo para levantamiento cero coeficiente, y un valor que aumenta lentamente del coeficiente de elevación máximo. Esto va acompañado de un ligero incremento en el coeficiente de arrastre y un incremento negativo en el coeficiente de momento de cabeceo en el centro aerodinámico a medida que aumenta la curvatura. En cursos posteriores de aerodinámica aprenderás a predecir estos cambios que resultan de la modificación de la forma de la línea de curvatura del perfil aerodinámico. Ahora es evidente, sin embargo, que el aumento de la inclinación puede dar mayores coeficientes de sustentación y tanto el diseñador del avión como el piloto tal vez deseen aprovechar esto. Un tipo de vuelo donde esto se vuelve muy útil es el vuelo a baja velocidad, especialmente en el despegue y aterrizaje.
Para volar el levantamiento del avión debe ser igual a su peso.
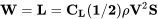
Esta relación dice que la elevación proviene de cuatro cosas, el coeficiente de sustentación, la densidad, la velocidad y el área planforme del ala. No hay mucho que podamos hacer con respecto a la densidad, viene con la altitud, y si bien hay formas de cambiar el área del ala mientras un avión está en vuelo, éstas suelen ser poco prácticas. Observamos que la velocidad es un factor poderoso ya que es cuadrada.
La ecuación anterior esencialmente nos dice que si queremos volar a menor velocidad con un ala y altitud dadas debemos aumentar el coeficiente de sustentación. Podemos hacer esto hasta cierto punto a medida que aumentamos el ángulo de ataque desde el ángulo de ataque de elevación cero hasta el ángulo de parada, pero el puesto define nuestro límite.
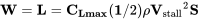
Nosotros, por supuesto, no queremos intentar volar a C Lmax porque nos detendremos, pero la velocidad de calado sí define el límite mínimo para nuestro posible rango de velocidad de vuelo a una altitud dada. Si queremos volar a menor velocidad necesitamos aumentar el valor de C Lmax. Las gráficas del Apéndice A nos muestran que esto se puede hacer con colgajos. En la parcela para el perfil aerodinámico NACA 1412 vemos que al desviar un flap dividido con una longitud del 20% de la cuerda aerodinámica a un ángulo de 60 grados podemos aumentar el coeficiente de sustentación máximo de 1.6 a 2.5, un cambio que bajaría nuestra velocidad de calada en un 20 por ciento. Esto significa que podemos volar a una velocidad 20% menor.
Este es un efecto poderoso pero no es gratuito. Se acompaña de un gran incremento en el coeficiente de arrastre y un enorme cambio en el momento de pitcheo. Esto puede significar la necesidad de un estabilizador horizontal o canard más grande para contrarrestar el cambio de tono y tendremos que lidiar con el arrastre.
En los primeros días del vuelo no había necesidad real de flaps. Los aviones volaron a velocidades muy lentas para los estándares actuales y sus velocidades de parada a menudo eran muy bajas debido a las grandes áreas de las alas. Pero a medida que la investigación mostró cómo reducir el arrastre de los aviones y mejores motores dieron cada vez más potencia y empuje no se necesitaba tanto área de ala para cruzar a las velocidades más altas resultantes. Los diseñadores de aviones descubrieron que hacer un crucero en avión a más de 200 mph y aún aterrizar a algo así como 60 mph o menos era un problema. La velocidad de aterrizaje es importante porque está directamente relacionada con la distancia de parada y la longitud de pista necesaria. Las velocidades de aterrizaje más altas también pueden aumentar el riesgo de accidentes de aterrizaje.
La mayoría de los aviones cruzan con un coeficiente de sustentación de aproximadamente 0.2 a 0.3 y los mejores perfiles subsónicos tendrán un C Lmax no superior a 1.8. Estos dos factores definen el problema del crucero de alta velocidad y el aterrizaje a baja velocidad.
En 1933 la compañía Boeing sacó a relucir el avión Boeing 247, un avión completamente moderno para su época que aprovechó todos los avances acumulados en el diseño de motores y fuselajes. Su velocidad de crucero fue de 188 mph a una altitud de 8000 pies. El 247 pesaba 13,650 libras y tenía un área de ala de 836 pies 2. Un cálculo rápido de su coeficiente de elevación de crucero da C L = 0.23, un valor razonable. En ese momento las pistas existentes requerían una velocidad de aterrizaje de alrededor de 60 mph y un cálculo del coeficiente de sustentación del 247 a nivel del mar a 60 mph da 1.77, bastante cerca del máximo para un ala convencional.
The Douglas Aircraft Company (ahora parte de Boeing) decidió construir un avión de pasajeros más grande y cómodo y salió con el DC-1, el prototipo de avión y el modelo de producción DC-2. El DC-2 pesaba 36% más que el 247 con 18,560 libras y tenía un área de ala ligeramente más alta de 939 pies 2, pero cruzó aproximadamente a la misma velocidad y altitud que su competidor. El crucero C L para el DC-2 sale a ser de aproximadamente 0.27, mayor que el 247 por su peso significativamente mayor. Esta mayor “carga de ala” dio a los pasajeros del DC-2 un viaje más cómodo que el 247.
Para aterrizar el DC-2 a 60 mph se requiere un C L de aproximadamente 2.15, demasiado alto para un ala normal. La solución fue agregar flaps, dando un comba extra y un C Lmax más alto cuando fue necesario para el aterrizaje y el despegue. Esto permitió que el DC-2 más grande y cómodo volara tan rápido como el 247 y aún aterrizar y despegar en todos los aeropuertos comerciales de su día. El DC-2 y su hermano aún más grande y cómodo, el DC-3, revolucionaron la industria aérea.
Cabe señalar que las grandes deflexiones del flap se utilizan en el aterrizaje donde la resistencia adicional puede ser realmente ventajosa y las deflexiones más pequeñas se utilizan en el despegue donde la resistencia más baja y la aceleración rápida son imprescindibles.


Hay muchos tipos de colgajos. Hay solapas tanto de borde de ataque como de borde de salida y una serie de variaciones en ambos. La teoría aerodinámica nos dice que un aumento de curvatura es más efectivo cuando se realiza cerca del borde de salida de un perfil aerodinámico, por lo tanto, el flap del borde de salida es el tipo principal de colgajo utilizado en las alas. La desviación de prácticamente cualquier tipo de flap de borde de salida de una placa plana simple a un sistema de flap complejo de múltiples elementos desplazará la “curva de elevación” hacia la izquierda y aumentará C Lmax. Algunos flaps de borde de salida tienen ranuras y múltiples elementos para ayudar a controlar el flujo sobre los flaps y evitar la separación para dar un coeficiente de sustentación aún mayor y, a menudo, estos flaps se despliegan de tal manera que agregan temporalmente área adicional del ala.
Los flaps de borde de ataque hacen poco para mover la curva de elevación hacia la izquierda, pero pueden hacer mucho para permitir que el perfil aerodinámico vaya a un ángulo de ataque más alto antes de detenerse, controlando el flujo sobre la “nariz” del perfil aerodinámico y retrasando la separación. Los flaps de borde de ataque se utilizan a menudo en el despegue y aterrizaje junto con los flaps del borde de salida. Algunos aviones han sido diseñados con aletas de borde de ataque o ranuras fijadas permanentemente en el ala para darles velocidades de pérdida más bajas.
Los efectos de ambos flaps de borde delantero y trasero se muestran en la siguiente figura.
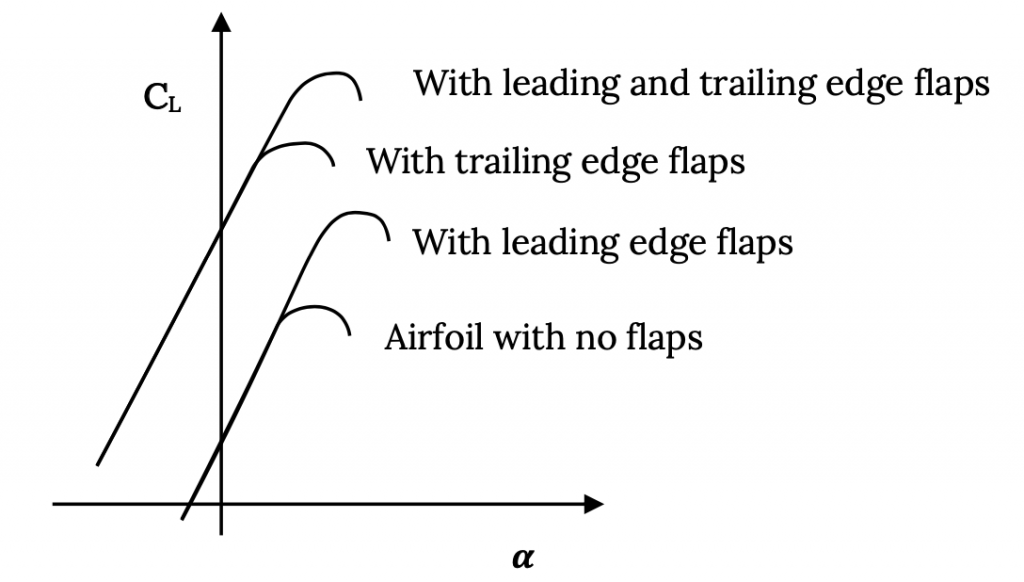
La siguiente tabla enumera las magnitudes típicas del coeficiente de sustentación con y sin solapas de borde delantero y trasero para un perfil aerodinámico “Clark Y”. El perfil aerodinámico Clark Y es una famosa forma de perfil aerodinámico que no es de NACA desarrollada por Virginius Clark. Clark había servido en la misma comisión que muchos de los fundadores de la NACA, una comisión encargada de estudiar secciones de perfil aerodinámico europeas después de la Primera Guerra Mundial y, utilizando gran parte de la misma información que la NACA utilizó para desarrollar sus perfiles aerográficos originales de 4 dígitos, Clark desarrolló el Clark Y y otros perfiles aerográficos como parte de su investigación de doctorado en el MIT. En el Clark Y, Virginius Clark diseñó una forma aerodinámica con un fondo plano que facilitaba su fabricación, y debido a esto y a su excelente desempeño aerodinámico, se utilizó ampliamente para todo, desde alas de avión hasta palas de hélice.

Tabla 1.3: Efectos de flap y ranura de borde de ataque y borde de salida en un perfil aerodinámico Clark Y
| Configuración | C sub Lmax | alpha sub stall |
|---|---|---|
| Perfil aerodinámico básico Clark Y | 1.29 | 15 |
| con solapa lisa 30% a 45° | 1.95 | 12 |
| con ranura “fija” y sin solapa | 1.77 | 24 |
| con ranura y solapa lisa | 2.18 | 19 |
| con 40% solapa Fowler a 40° | 3.09 | 14 |
| con ranura desplegable y solapa Fowler | 3.36 | 16 |
En resumen, un flap de borde de salida puede tener un “efecto de comba” significativo; es decir, puede desplazar la “curva de elevación” hacia la izquierda, aumentando el ángulo de ataque de elevación cero y el valor de C Lmax. También se puede desplegar de tal manera que aumente temporalmente el área del ala. Un flap o ranura de borde de ataque probablemente no producirá un “efecto de comba” (si lo hace, es probable que sea uno “negativo”, desplazando ligeramente la “curva de elevación” hacia la derecha) pero ayudará a retardar la parada a un ángulo de ataque más alto ya sea que se use en un ala con o sin flaps.
1.19 Alas y alas transónicas y supersónicas
Anteriormente vimos la forma en que el flujo puede acelerar a velocidades supersónicas sobre un perfil aerodinámico o un ala a medida que la velocidad de flujo libre se acerca a la velocidad del sonido y cómo, a números de Mach superiores a algún “número crítico de Mach”, la desaceleración de ese flujo supersónico de regreso a velocidades subsónicas puede resultar en un flujo repentino separación y aumento de arrastre. Hay dos formas de reducir este arrastre. Una es barriendo el ala y la otra es diseñando una sección especial de superficie aerodinámica.
1.20 Barrido de ala
La primera forma encontrada para disminuir con éxito la subida de arrastre que se produce en el régimen de vuelo transónico es barriendo el ala. La teoría y el experimento mostraron que tanto el inicio como la magnitud del incremento de arrastre fueron funciones del “componente normal” del número de Mach de flujo libre, M∞. En otras palabras, si un ala es barrida 45 0 el componente normal del número Mach de flujo libre es M∞ coseno θ o 0.707
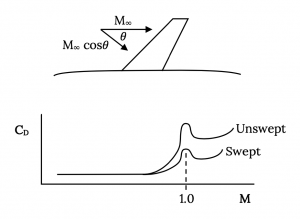
Al igual que con casi todo este beneficio de barrido tiene un costo. El barrido del ala también reduce su coeficiente de sustentación en un ángulo de ataque dado (reduce la pendiente de la curva de sustentación) y el flujo curvo sobre el ala misma puede conducir a una pérdida prematura cerca de las puntas del ala y un fenómeno conocido como “pitch up”
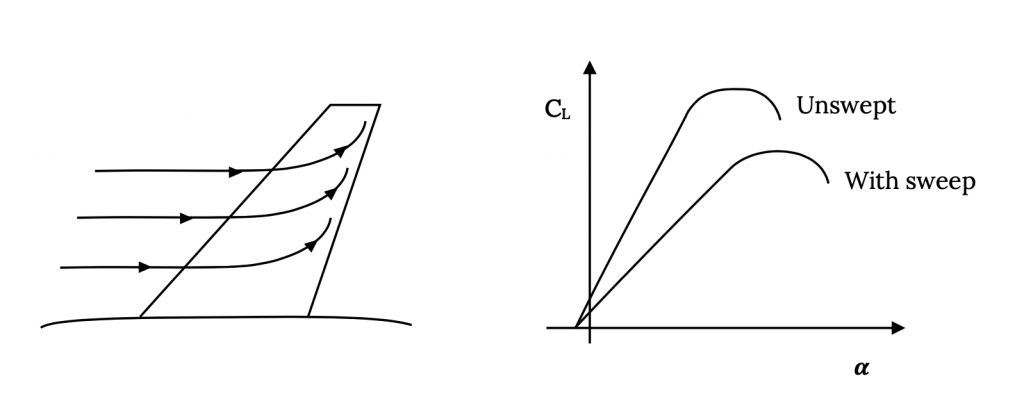
Si bien la mayoría de las alas barridas están inclinadas hacia la parte trasera del avión o barridas hacia atrás, teóricamente no importa si el ala está barrida hacia adelante o hacia atrás. Varios diseños de alas barridas tempranas se dibujaron con alas barridas hacia adelante que permitieron que el larguero o estructura del ala pasara a través del fuselaje a popa de la cabina y presentaban menos problemas de diseño interno, pero pronto se descubrió que efectivamente había un problema con las alas barridas hacia adelante. Este problema fue causado por el mismo tipo de flujo curvo que provocó el estancamiento de la punta en las alas barridas de popa excepto que el resultado en el ala barrida hacia adelante fue una elevación adicional en las puntas de las alas que tendía a torcer las alas hasta su punto de ruptura a velocidades bastante bajas. No tenía mucho sentido barrer un ala para bajar la subida de arrastre transónico cuando el ala se rompería mucho antes de que se alcanzaran tales velocidades y el peso agregado necesario para endurecer el ala y evitar fallas hacía que los aviones fueran demasiado pesados. Este problema finalmente se resolvió en la década de 1970 con el uso de estructuras compuestas a base de tela que podrían diseñarse de tal manera que el ala se fortaleciera a medida que intentaba retorcerse. El avión experimental X-29 demostró con éxito que las alas barridas hacia adelante podrían ser utilizadas en flujos transónicos.
1.21 Perfiles supercríticos
El otro método utilizado para reducir la subida de arrastre transónico en un ala fue desarrollado por Richard Whitcomb en el Centro de Investigación NASA-Langley en la década de 1960. El Dr. Whitcomb esencialmente remodeló la sección aerodinámica convencional para hacer tres cosas. Aumentó la “redondez” del borde de ataque del perfil aerodinámico para dar una aceleración más gradual del flujo a una velocidad menor que las formas convencionales del perfil aerodinámico por lo que cuando el flujo supersónico resultó en la superficie era más débil. Redujo la curvatura del ala en su área media de cuerda para aplanar la superficie superior y permitir una región más larga de este flujo supersónico más débil antes de permitirle desacelerar, dando menos separación y arrastre. Finalmente, para compensar el levantamiento que se perdió al diseñar un flujo de superficie superior más lento, Whitcomb diseñó su superficie aerodinámica con una significativa “curvatura de popa” en su superficie inferior, señalando que la curvatura tiene un efecto muy potente limpiando un borde de salida de perfil aerodinámico. El resultado fue un perfil aerodinámico algo parecido al de abajo que dio un excelente desempeño aerodinámico con una disminución de la elevación de la resistencia transónica. Este tipo de superficie aerodinámica se llama un perfil aerodinámico Whitcomb o un perfil aerodinámico “supercrítico”.

Al final resultó que este perfil aerodinámico era un excelente diseño para todos los rangos de vuelo con su único inconveniente siendo una tendencia hacia un gran momento de cabeceo debido a la inclinación inferior de popa. Los diseños posteriores han reducido este problema y las variantes de este diseño se utilizan en casi todos los tipos de aviones hoy en día.
Al hablar de Richard Whitcomb y el flujo transónico, también debe mencionarse su diseño de fuselaje de “botella de coque”. A principios de la década de 1950 cuando los cazas a reacción se acercaban a Mach 1 en capacidad, el ascenso transónico de arrastre de todo el avión siguió siendo un problema para “romper la llamada barrera del sonido”. Convair y la Fuerza Aérea esperaban que un nuevo caza de ala delta, altamente barrido, designado el F-102 pudiera volar rutinariamente a velocidades supersónicas; sin embargo, dos aviones prototipo no lograron llegar al Mach 1. Whitcomb se dio cuenta de que, a la velocidad del sonido, el aire no se puede comprimir más y necesita algún lugar a donde ir o simplemente empujará hacia afuera del avión, desplazando otro flujo de aire y provocando arrastre. Sugirió un rediseño del fuselaje F-102 con una sección transversal reducida en las inmediaciones del ala para permitir que este aire supersónico vaya a un lugar sin alejar los flujos exteriores. El fuselaje “wasp-waist” o “coke-bottle” fue el resultado y el diseño que antes no podía llegar a la velocidad del sonido alcanzó Mach 1.22 en su primer vuelo.
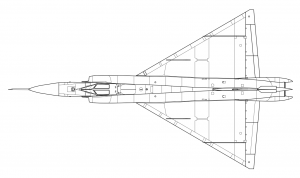
1.22 Aerodinámica Tridimensional
La mayoría de las cosas discutidas en las secciones anteriores fueron fenómenos bidimensionales como el diseño de la sección aerodinámica, los efectos de la curvatura, etc. El barrido del ala fue la excepción. Pero hay muchas otras variaciones en la forma y forma del ala que influirán en el rendimiento aerodinámico de un ala. Empecemos por mirar la Relación de Aspecto.
Un ala que esté produciendo sustentación debe tener una presión menor en su superficie superior que en la superficie inferior. En las puntas del ala no hay nada que impida que el aire de la superficie inferior intente rodear la punta del ala hasta la superficie superior donde la presión inferior actúa como un vacío. El resultado es cierta pérdida de sustentación cerca de la punta del ala. Un ala ideal tendría la misma sustentación desde la punta del ala hasta la punta del ala pero un ala real no.
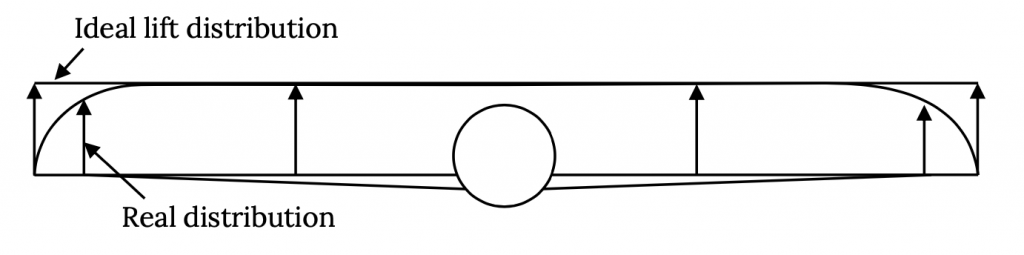
Esta pérdida de sustentación se siente por cierta distancia al interior de las puntas del ala. La pregunta es qué porcentaje del área del ala afecta esto y esto dependerá de la Relación de Aspecto del ala, AR.
La relación de aspecto es una medida de la envergadura del ala dividida por su acorde “media” o promedio. También se puede expresar en términos del cuadrado del tramo y el área de forma plana.
AR = b 2/S = b/ c promedio
donde b = envergadura del ala, S = área en forma de planta, c = cuerda
Para ver por qué la relación de aspecto es importante, podemos observar dos formas planas de ala diferentes de la misma área pero diferentes relaciones de aspecto.
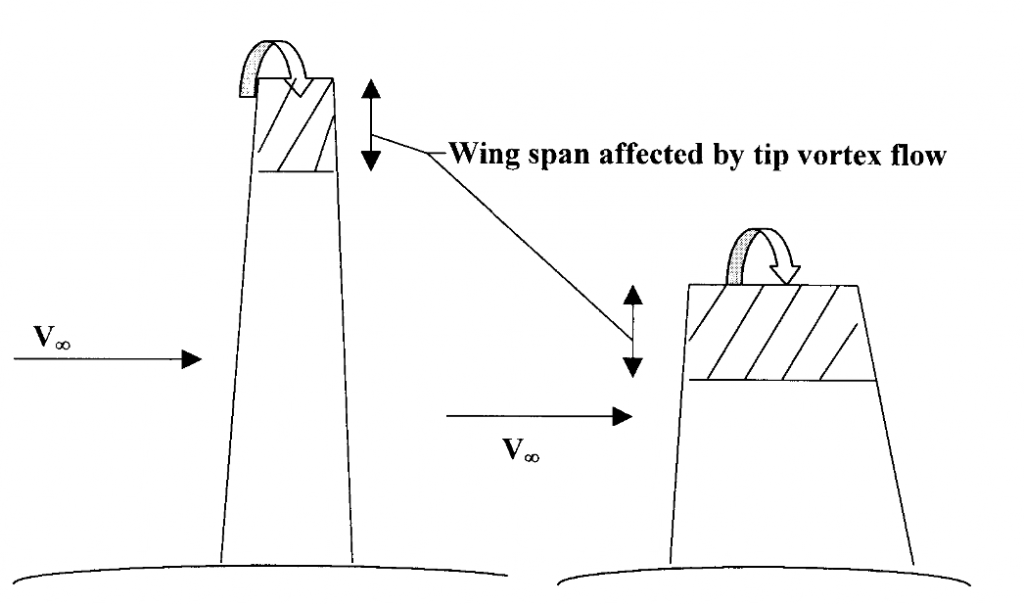
Este flujo alrededor de la punta del ala da como resultado otros dos problemas, la producción de un arrastre llamado arrastre inducido y la creación de un flujo arremolinado similar a un tornado, llamado vórtice de punta de ala detrás de la punta del ala que puede ser un peligro para el seguimiento de la aeronave.
Los vórtices de arrastre (un vórtice por cada punta del ala) pueden continuar por millas detrás de una aeronave y la “fuerza” de los vórtices dependerá del peso de la aeronave generadora. Un avión siguiente, particularmente uno pequeño, puede encontrarse repentinamente al revés (o peor) si se encuentra con uno de estos vórtices. Esto es particularmente peligroso cerca del suelo y es una de las razones de los tiempos de separación requeridos entre el aterrizaje y el despegue de los aviones en los aeropuertos.
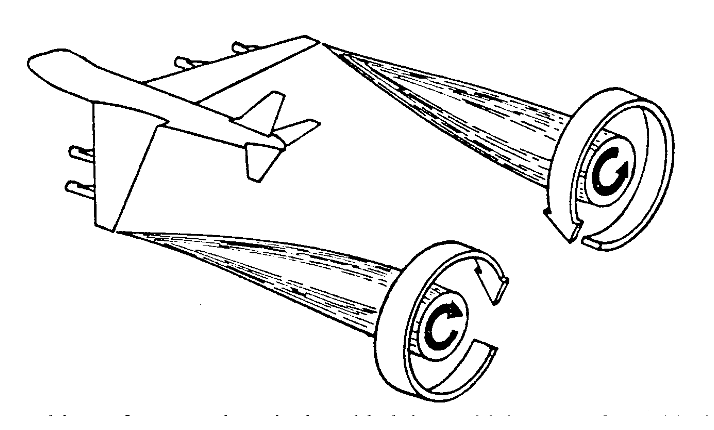
El problema 3-D de preocupación aquí es el arrastre agregado que proviene de este flujo alrededor de las puntas de las alas y la disminución de la elevación. Debido a este flujo, el coeficiente de sustentación en un ala 3-D será menor en un ángulo de ataque dado que una sección de superficie aerodinámica 2-D de la misma forma. La teoría aerodinámica se puede utilizar para calcular el efecto 3-D en función de la forma plana del ala y ese efecto se puede caracterizar como un efecto de relación de aspecto. Se dice que una sección de superficie aerodinámica 2-D tiene una relación de aspecto infinita y para la teoría de casos 2-D da una pendiente para la “curva de elevación” (DCL/Dα) de 2π. Para el caso 3-D donde la relación de aspecto es finita, se encontrará que la pendiente de la curva de elevación disminuye con la relación de aspecto decreciente.
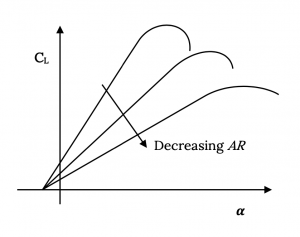
El arrastre agregado en 3-D proviene del mismo fenómeno que provoca la elevación. Definimos la vida como una fuerza perpendicular a la velocidad de la corriente libre. El arrastre inducido es una fuerza que es perpendicular a la velocidad de “downwash” causada por el flujo alrededor de la punta del ala. Esta velocidad de downwash es pequeña en comparación con el flujo de flujo libre y el arrastre inducido es correspondientemente pequeño pero sigue siendo una fuerza que necesitamos entender y tratar.
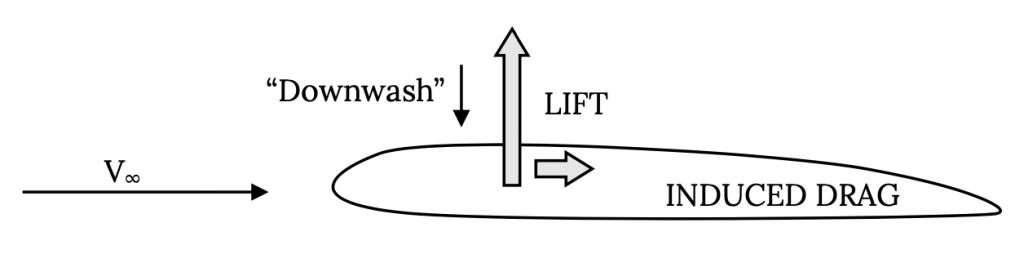
La teoría mostrará que el coeficiente de arrastre inducido C Di es:
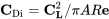
A partir de esto se puede observar que a medida que el AR aumenta la resistencia inducida disminuye y que en el caso 2-D donde la relación de aspecto teórica es infinito, el coeficiente de arrastre inducido es cero. Pero, ¿qué pasa con el otro término en la ecuación, e?
e se llama el “factor de eficiencia de Oswald”. El valor de e estará en algún lugar entre cero y uno siendo uno el mejor o “arrastre inducido mínimo” caso. La teoría mostrará que e es una función de la forma en que la elevación actúa a lo largo del tramo del ala, que es una función de varias cosas, incluyendo la forma en forma de plano del ala, el barrido del ala, la torsión del ala, la conicidad, las diversas secciones del perfil aerodinámico utilizadas a lo largo del tramo, etc. Un estudio de esta teoría mostrará que el mejor de los casos, cuando e = 1.0 ocurre cuando la elevación se distribuye a lo largo de la envergadura del ala de manera elíptica. Este caso de arrastre inducido mínimo a menudo se llama el caso de distribución de elevación elíptica.
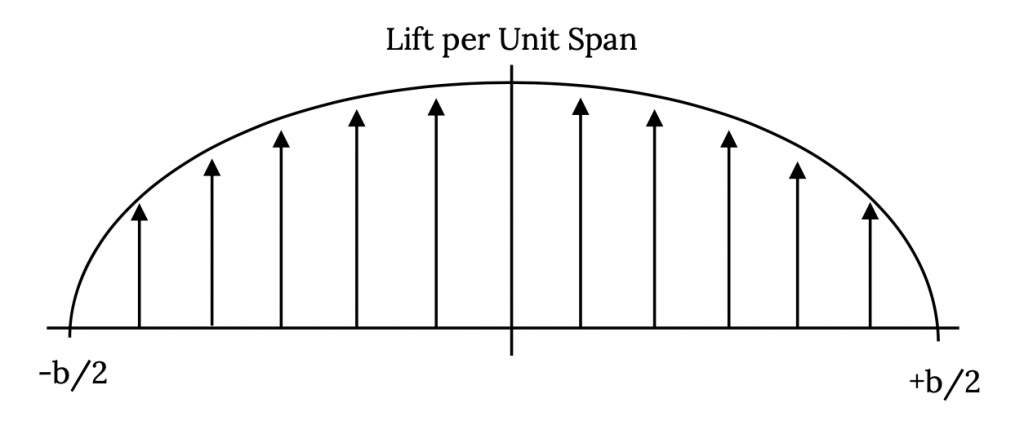
Hay muchas maneras de obtener una distribución de elevación elíptica. Lo más fácil de visualizar es que donde la forma del plano del ala tiene forma de elipse, es decir donde la cuerda del ala varía elípticamente a lo largo de su envergadura. En la década de 1940 muchos combatientes de la Segunda Guerra Mundial fueron construidos con formas planas elípticas para tratar de minimizar el arrastre inducido. El más famoso de estos fue el avión británico Spitfire.

Es posible obtener una distribución de elevación elíptica o casi elíptica de otras maneras con la combinación correcta de conicidad del ala, giro y barrido o variando la sección aerodinámica utilizada a medida que sale del tramo. Algunas de estas combinaciones pueden dar valores de coeficiente de arrastre inducido en o cerca de un mínimo mientras minimizan la dificultad de construir el ala. En algunos casos se requiere una planform complicada por otras razones como “sigilo” o minimizar el retorno del radar de la aeronave. El bombardero B-2, “sigiloso”, a pesar de su forma de ala en forma de “diente de sierra”, tiene una distribución de elevación casi elíptica.
A menudo, el giro es parte de este esquema porque también puede ser necesario para el control en el puesto. Debido a que las superficies de control utilizadas para el control de balanceo, los alerones, están cerca de las puntas del ala queremos diseñar el ala para que la parte exterior del ala no se detenga cuando la sección interior comience a pararse. Por esta razón, la parte del ala cerca de la punta suele estar retorcida para darle un ángulo de ataque menor que el resto del ala. Algunos aviones utilizan diferentes secciones aerodinámicas cerca de la punta que en el resto del ala por esta razón.
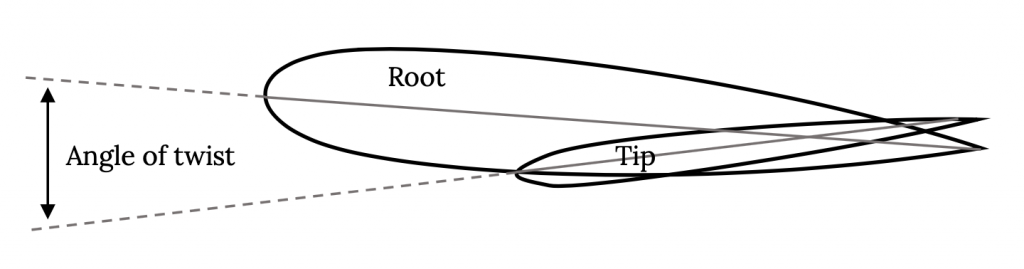
Cabe destacar que si bien la distribución de sustentación elíptica es ideal aerodinámicamente existen otros factores que deben tenerse en cuenta a la hora de diseñar el ala. Por ejemplo, otra distribución de elevación puede ser la óptima para la resistencia estructural o para la capacidad de respuesta de control. El británico Spitfire era un avión muy eficiente aerodinámicamente debido a su planform de ala elíptica pero los pilotos encontraron que no podían rodar al luchador tan rápido como sus oponentes alemanes en peleas de perros. Como resultado, la hermosa ala de Spitfire fue “recortada” en versiones posteriores para permitir mayores tasas de balanceo porque en el mundo real de la guerra aérea se encontró que la maniobrabilidad era más importante que la eficiencia aerodinámica y el arrastre.
También hay que destacar que el arrastre inducido es sólo una porción del arrastre. Este “arrastre por elevación” es independiente de otras fuentes de arrastre como la fricción entre el aire y la “piel” o superficie de la aeronave o la “resistencia a la presión” que proviene de la variación normal de presiones alrededor del perfil aerodinámico. Estos otros tipos de arrastre deben calcularse a partir de la teoría aerodinámica y la teoría de la “capa límite”, las asignaturas de dos cursos posteriores en el plan de estudios.
Testa 1
1. Escriba una calculadora o programa de computadora para encontrar las condiciones atmosféricas estándar (presión, temperatura y densidad) para cualquier altitud en la troposfera y estratosfera tanto en unidades SI como inglesas. Entregue un listado del programa y una impresión para condiciones cada 1,000 metros (unidades SI) y cada 1000 pies (unidades en inglés) hasta 100,000 pies o 30,000 metros.
2. Un tanque de aire comprimido está equipado con una ventana de 150 mm de diámetro. Un manómetro de tubo en U que utiliza mercurio como fluido de operación está conectado entre el tanque y la atmósfera y lee 1.80 metros. ¿Cuál es la carga total que actúa sobre los tornillos que fijan la ventana? La densidad relativa del mercurio es 13.6.
3. En un día determinado la presión y la temperatura del nivel del mar son 101,500 N/m 2 y 25°C, respectivamente. Se encuentra que la temperatura desciende linealmente con altitud a -55°C a 11,300 metros y es constante por encima de esa altitud.
4. Una aeronave sin errores de instrumento y con un altímetro calibrado según las especificaciones ISA tiene una lectura de altímetro de 5000 metros. ¿Cuál es la altitud real de la aeronave? ¿Qué altitud mostraría el altímetro cuando el avión aterrice al nivel del mar?
Referencias
Cuadros 1.1 y 1.2: Comité Consultivo Nacional de Aeronáutica (1953). NACA-TR-1135 y NACA TN 1428. Recuperado a partir de https://ntrs.nasa.gov/citations/19930091059
Figura 1.1: Gris Kindred (2021). “Terminología de superficie aerodinámica”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.1_20210804
Figura 1.2: Gris Kindred (2021). “Terminología de Planform del Ala”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.2_20210804
Figura 1.3: Gris Kindred (2021). “Algunas Formas Planformes de Alas”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.3_20210804
Figura 1.4: Gris Kindred (2021). “Un Típico Altímetro Mecánico Sensible”. CC BY-SA 3.0. Adaptado de WikiDot (2009). “Figura 4: El Mecanismo”. CC BY-SA 3.0. Original: http://aviationknowledge.wikidot.com/aviation:sensitive-altimeters. Adaptado: https://archive.org/details/1.4_20210804
Figura 1.5: James F. Marchman (2004). “Ejemplo de Ecuación de Bernoulli”. CC BY 4.0.
Figura 1.6: James F. Marchman (2004). “Un Tubo Pitot Mide la Presión Total”. CC BY 4.0.
Figura 1.7: James F. Marchman (2004). “Un Tubo Estático Mide la Presión Estática”. CC BY 4.0.
Figura 1.8: Gris Kindred (2021). “Una Sonda Pilot-Estática”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.8-updated
Figura 1.9: Gris Kindred (2021). “Un indicador de velocidad aérea”. CC BY 4.0. Adaptado del Manual Piloto de Conocimiento Aeronáutico de la Administración Federal de Aviación. Dominio público. Original disponible en https://www.faa.gov/regulations_policies/handbooks_manuals/aviation/phak/media/10_phak_ch8.pdf. Adaptado disponible en: https://archive.org/details/1.9_20210804
Figura 1.10: Gris Kindred (2021). “Formación de Ondas de Choque en Flujo “Transónico”.” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.10_20210804
Figura 1.11: Gris Kindred (2021). “Aumento del coeficiente de arrastre cerca de Mach One”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.11_20210804
Figura 1.12: NASA (1947). “Campana X-1 46-062 (en vuelo).” Dominio público. Disponible en https://commons.wikimedia.org/wiki/File:Bell_X-1_46-062_(in_flight).jpg
Figura 1.13: Gris Kindred (2021). “Flujo Alrededor de un Cilindro Circular”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.13_20210804
Figura 1.14: Gris Kindred (2021). “Variación del coeficiente de arrastre con número de Reynolds para una esfera”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.14_20210804
Figura 1.15: Gris Kindred (2021). “Definición del Signo de Momento de Pitching”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.15_20210804
Figura 1.16: Gris Kindred (2021). “Relación entre la velocidad de elevación, arrastre y flujo libre”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.16_20210804
Figura 1.17: Gris Kindred (2021). “Gráficas de Coeficiente de Elevación y Arrastre Versus alfa, Mostrando Puesto (a).” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.17_20210804
Figura 1.18: James F. Marchman (2004). “Tipo de Distribución de Presión”. CC BY 4.0.
Figura 1.19: Arcos SDASM (2013). “Boeing 247”. Los Comunes. Disponible en https://www.flickr.com/photos/sdasmarchives/11343397173/
Figura 1.20: Björn Strey (2009). “Douglas DC-2 (PH-AJU) en vuelo en el Aeropuerto de Bremen Flugtag (3519224016).” CC BY-SA 2.0. Disponible en https://commons.wikimedia.org/wiki/File:Douglas_DC-2_(PH-AJU)_in_flight_at_the_Bremen_Airport_Flugtag_(3519224016).jpg
Figura 1.21: Gris Kindred (2021). “Efectos típicos de solapa de borde delantero y trasero”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.21_20210804
Figura 1.22: James F. Marchman (2004). “La forma de perfil aerodinámico Clark Y”. CC BY 4.0.
Figura 1.23: Gris Kindred (2021). “Efectos generales del barrido del ala en la subida de arrastre transónico”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.23_20210804
Figura 1.24: Gris Kindred (2021). “Otros Efectos del Barrido Ala (a)”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.24_20210804
Figura 1.25: Gris Kindred (2021). “Forma Supercrítica de la superficie aerodinámica”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.25_20210804
Figura 1.26: Kaboldy (2012). “Daga Delta Convair F-102”. CC BY-SA 3.0. Disponible en https://commons.wikimedia.org/wiki/File:Convair_F-102_Delta_Dagger.svg
Figura 1.27: Gris Kindred (2021). “Distribuciones de Elevación Ideal (2-D) y Real (3-D) en un Ala”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.27_20210804
Figura 1.28: James F. Marchman (2004). “El ala AR alta a la izquierda tiene menos área afectada por el flujo alrededor de la punta y, por lo tanto, menos pérdida de sustentación que el ala AR inferior a la derecha. a).” CC BY 4.0.
Figura 1.29: James F. Marchman (2004). “Vórtices de arrastre”. CC BY 4.0.
Figura 1.30: Gris Kindred (2021). “La “pendiente” de la curva de elevación disminuye a medida que disminuye la AR”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.30_20210804
Figura 1.31: Gris Kindred (2021). “Downwash y Arrastre Inducido”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.31_20210804
Figura 1.32: Gris Kindred (2021). “Una distribución de elevación elíptica”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.32_20210804
Figura 1.33: Gris Kindred (2021). “El avión británico 'Spitfire'”. CC BY-SA 2.0. Adaptado de Falcon Photography (2019). “Carenado de Vientre Spitfire”. CC BY-SA 2.0. Original disponible en https://www.flickr.com/photos/falcon_33/48712711406/in/photostream/. Adaptado disponible en https://archive.org/details/1.33_20210804
Figura 1.34: Gris Kindred (2021). “A menudo, las alas se tuercen para evitar que el área de la punta se detenga cuando el ala interior se detiene, así como para dar una distribución de elevación de arrastre inducida baja a lo largo del tramo”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/1.34_20210804
<! — pb_fixme —><! — pb_fixme —>


