3: Herramientas adicionales de aerodinámica

Introducción

Todos los conceptos aerodinámicos introductorios necesarios para que el material de rendimiento de la aeronave sea cubierto en los siguientes capítulos se presentaron en el Capítulo 1. En general, se dejará a la elección de los lectores de muchos textos excelentes sobre el tema de la aerodinámica proporcionar una cobertura en profundidad del campo, incluyendo derivaciones completas de teorías aerodinámicas y discusiones sobre su uso. El campo de la aerodinámica suele separarse en cinco o más segmentos en función de las características de flujo y los supuestos que pueden o deben hacerse para analizar esos flujos en detalle. Estas divisiones normalmente incluirían:

• Aerodinámica incompresible o subsónica
• Aerodinámica transónica
• Aerodinámica supersónica
• Aerodinámica hipersónica
• Teoría de la capa límite

Otros segmentos del campo aerodinámico, aún más especializados, podrían incluir temas como la dinámica de gases enrarecidos y la magnetohidrodinámica.

En el capítulo uno analizamos algunos conceptos básicos relevantes para los tres primeros temas anteriores con énfasis en el régimen de flujo incompresible y, ojalá, suficiente discusión de los supuestos involucrados para que el lector reconozca cuando está en peligro de la necesidad de dar cuenta del flujo transónico o supersónico efectos. Analizamos algunas de las conclusiones básicas que provienen de un análisis del flujo bidimensional y tridimensional alrededor de perfiles aerodinámicos y alas. Aprendimos, por ejemplo, que la curvatura de un perfil aerodinámico determinará el ángulo de ataque en el que el coeficiente de sustentación del perfil aerodinámico es cero y que podemos cambiar temporalmente la curvatura con cosas como la deformación del ala o su equivalente moderno, “morphing”, o, de una manera más convencional con flaps. Quizás tengamos curiosidad por saber cuánto puede dar una inclinación de cambio en el ángulo de ataque de elevación cero.

Aprendimos que existe un cierto tipo de distribución de sustentación en el sentido de la envergadura en un ala tridimensional que dará un rendimiento aerodinámico “óptimo” al dar “arrastre inducido mínimo” y encontramos que las formas planas de las alas con mayor relación de aspecto también dan un mejor rendimiento que las alas con baja AR.

En este capítulo vamos a echar un vistazo muy elemental a estos dos efectos fundamentales de configuración de ala y perfil aerodinámico, solo lo suficiente para que tengamos al menos una o dos herramientas básicas que podrían ayudarnos a averiguar algo sobre los efectos del diseño del ala en el rendimiento de la aeronave en caso de que necesitemos hacerlo. Esto lo haremos, no a través del tipo de análisis exhaustivo que se encontraría en la mayoría de los buenos libros de texto aerodinámicos, sino con un par de enfoques algo sobresimplificados que, sin embargo, suelen ser útiles.

Con el fin de desarrollar los métodos deseados de “fondo de la envolvente” para observar algunas influencias básicas del perfil aerodinámico y la forma del ala en la aerodinámica y el rendimiento, primero debemos echar un vistazo rápido a cómo un aerodinamista haría un modelo matemático de un ala o perfil aerodinámico. Comencemos por mirar el flujo alrededor de un perfil aerodinámico de elevación.

3.1 Aerodinámicas (2-D Aerodinámica)

Para que una superficie aerodinámica o un ala levanten el producto, el flujo sobre su superficie superior debe moverse más rápido que el flujo sobre su superficie inferior. Si esto ocurre, la ecuación de Bernoulli nos diría que el flujo más rápido sobre la superficie superior dará una presión menor que el flujo más lento sobre la superficie inferior y este diferencial de presión producirá elevación. Si miramos el flujo en un punto a cierta distancia detrás del borde de ataque de un perfil aerodinámico encontraremos que podríamos representarlo algo como se muestra en la figura de abajo con un vector de velocidad grande en la parte superior del perfil aerodinámico y uno más pequeño en la parte inferior.

Otra forma de representar este mismo flujo sería con una combinación de un flujo “uniforme” y un flujo circular, de tal manera que las velocidades sumen en la parte superior del ala y resten en la parte inferior como se muestra a continuación.

Si se puede decir que estos dos flujos terminan dando el mismo resultado, se puede decir que el flujo mostrado en la Figura 3.2 es una forma de modelar el flujo alrededor de un perfil aerodinámico. Esto, de hecho, funciona muy bien y es la idea básica detrás de la forma en que un aerodinamista modelaría el flujo alrededor de un perfil aerodinámico.

Podríamos observar las velocidades de la superficie superior e inferior en varios puntos a lo largo de la cuerda y encontrar que en cualquier punto podemos modelar ese flujo local mediante un flujo “uniforme” y un flujo de tipo circular como se muestra en la Figura 3.3.

En este modelo, los flujos “uniformes” en la superficie superior e inferior serían exactamente los mismos que la velocidad aguas arriba o “freestream”, V _∞. Lo único que cambiaría en cada posición a lo largo de la línea de cuerda sería el flujo de tipo circular, que se volvería más potente donde el diferencial de velocidad entre las superficies superior e inferior se hace más grande y menos a medida que se hace más pequeño.

Estos flujos “circulares” se conocen como vórtices (un solo flujo circular es un vórtice) y son el equivalente matemático de un pequeño tornado. Resulta que los vórtices son flujos muy importantes en la aerodinámica y ocurren físicamente en muchos lugares. Por supuesto, no hay vórtices en medio de un ala. Aquí, solo estamos usando un flujo físico real, un vórtice, para crear un modelo matemático que nos dé el resultado que sabemos que realmente existe.

Estos flujos o vórtices puramente circulares pueden describirse matemáticamente en términos de su circulación. La circulación está técnicamente relacionada con la integración de una velocidad alrededor de un camino cerrado, concepto que no necesitamos entrar aquí y se le da un símbolo gamma [γ o γ]. La forma minúscula de la letra griega, γ, se usa cuando estamos combinando los efectos de muchos pequeños vórtices y la forma mayúscula, γ, se usa ya sea cuando solo hay un solo vórtice o cuando estamos viendo el efecto combinado de muchos pequeños vórtices. La circulación, gamma, es esencialmente la medición de la velocidad de rotación del flujo giratorio en un vórtice y a veces se le llama la fuerza de un vórtice.

Entonces, el concepto básico aquí es que para obtener un flujo de elevación (mayor velocidad en la parte superior y menor velocidad en la parte inferior) combinamos un flujo de vórtice con un flujo uniforme. Si hacemos esto y analizamos matemáticamente el resultado encontraremos una relación muy importante y muy sencilla entre la elevación producida y la circulación y velocidad de flujo libre que dice:

Elevación = ρ V _∞ γ

La elevación es igual a la densidad de flujo multiplicada por la velocidad de la corriente libre por la circulación. Puedes encontrar una derivación bien hecha de este principio básico en cualquier libro de texto de buena aerodinámica y ahí también encontrarás que este concepto es tan importante que se le da un nombre, el Teorema de Kutta-Joukowski.

Como siempre, debemos mirar las unidades involucradas con este parámetro, la circulación. Debemos tener en cuenta que miramos este concepto de flujo de tipo circular como una forma de mirar la elevación en una rebanada bidimensional de un ala, una sección aerodinámica. Entonces, el elevador del que estamos hablando es el levantamiento por unidad de lapso del ala; es decir, el levantamiento por pie o elevación por metro. Sabiendo eso, podemos ver cuáles deben ser las unidades de gamma.

Elevación (libras por pie) = densidad (babosas por pie cúbico) x velocidad (pies por segundo) x gamma

Equiparar las unidades en esta relación nos dice que las unidades para gamma deben ser:

(lb/ft) ÷ [(sl/ft ³) (pies/seg)] = (lb ft seg) /sl

y sabiendo que F = ma; es decir, 1 lb = 1 sl pies/seg ², encontraremos las unidades para gamma para que sean

unidades para γ = ft ²/seg.

Quizá estas unidades nos parezcan un poco extrañas. No son ni unidades de velocidad ni de aceleración. Sin embargo, eso está bien, porque la circulación no es velocidad ni aceleración, ¡es circulación!

Entonces, ¿qué hacemos con esto? Si esto fuera un curso riguroso de aerodinámica o texto tomaríamos unos miles de estos pequeños tornados (vórtices) y los pondríamos uno al lado del otro a lo largo de la cuerda o línea de curvatura de nuestra sección aerodinámica y haríamos un cálculo complicado para ver exactamente qué valor de gamma debe tener cada uno para dar la elevación correcta para un perfil aerodinámico de una forma dada en un ángulo de ataque dado al flujo de corriente libre. Basaríamos esto en la forma que queríamos que tuviera nuestra línea de curvatura aerodinámica. Finalmente, sumaríamos o “integraríamos” las circulaciones combinadas (gammas) para todos nuestros pequeños vórtices y encontraríamos la elevación total en la superficie aerodinámica.

También veríamos la “distribución” de esas circulaciones o fortalezas de vórtice y encontraríamos lo que podríamos llamar su “centroide” de vorticidad; es decir, el lugar en la cuerda aerodinámica donde se podría decir que actúa la elevación total si todos los pequeños vórtices pudieran ser reemplazados por un solo vórtice grande. Llamaríamos a este lugar el “centro de ascensor”.

Si hicimos todo esto (y, nuevamente, podemos encontrar esta derivación en todo su esplendor en cualquier buen texto de aerodinámica), encontraremos algunos resultados interesantes y muy útiles que enumeraremos a continuación:

Para una superficie aerodinámica “simétrica” (sin curvatura)

• El “centro de elevación” está en el “cuarto de cuerda”; es decir, una cuarta parte de la distancia a lo largo de la línea de cuerda desde el borde de ataque.
• El coeficiente de elevación bidimensional será C _L = 2πα donde α es el ángulo de ataque (ángulo entre la línea de cuerda y el vector de velocidad de corriente libre).

Para una superficie aerodinámica abombada (no simétrica)

• El “centro de elevación” no está en el cuarto de cuerda y, de hecho, se mueve a medida que cambia el ángulo de ataque.
• El coeficiente de elevación bidimensional ahora será C _L = 2 π (α — α _L0), donde α _L0 se llama el “ángulo de ataque de elevación cero” y es un ángulo negativo para una superficie aerodinámica positivamente acodada. Esto significa que la curva de sustentación se desplaza hacia la izquierda a medida que aumenta la curvatura y que, en un ángulo de ataque dado, el perfil aerodinámico combado producirá un coeficiente de sustentación mayor que el perfil aerodinámico simétrico (siempre que el perfil aerodinámico esté en un ángulo de ataque por debajo del de la calada).

Hablamos de estos mismos resultados en el Capítulo Uno sin decir mucho sobre sus orígenes. Este cambio en la curva de sustentación y el aumento del coeficiente de sustentación al aumentar la curvatura es la base para el uso de flaps como una forma temporal de aumentar el coeficiente de sustentación cuando se necesita un impulso en la capacidad de elevación, como en el aterrizaje.

La teoría aerodinámica que predeciría todo esto se llama “teoría del perfil aerodinámico” y lo hace precisamente como se describió anteriormente, asumiendo que miles de diminutos vórtices se colocan uno al lado del otro en lo que se llama una lámina de vórtices a lo largo de la línea de curvatura del perfil aerodinámico. Conociendo la descripción matemática de la forma de la línea de curvatura deseada, la velocidad del flujo libre y el ángulo de ataque, y requiriendo que no haya flujo a través de la línea de curvatura y que el flujo no vaya de una superficie a otra alrededor del borde de salida, la teoría del perfil aerodinámico delgado puede decir lo necesario distribución de la circulación a lo largo de la línea de curvatura desde el borde de ataque hasta el borde posterior para dar una simulación del flujo real alrededor del perfil aerodinámico.

Este método no puede predecir la parada. Para ello necesitaríamos considerar los efectos de cizallamiento o viscosidad en el flujo y esto requeriría que observáramos la “capa límite” o región de flujo viscoso alrededor de la superficie real del ala. Esto también, va mucho más allá del alcance del material que queremos investigar en este texto.

Entonces, ¿hay una manera simple de predecir los efectos de la curvatura sin recurrir a la teoría del perfil aerodinámico delgado de algún procedimiento igualmente desordenado? Resulta que existe un método de “parte posterior del sobre” llamado “Aproximación de Weissinger”

3.2 Aproximación de Weissinger

La aproximación de Weissenger se basa en los resultados simétricos del perfil aerodinámico de la teoría del perfil aerodinámico delgado que se enumeraron en una sección anterior. Estos resultados dicen que para una superficie de sustentación simétrica (esencialmente una placa plana) la elevación actúa en el cuarto de cuerda y el coeficiente de sustentación es 2-pi veces el ángulo de ataque.

También tenemos el Teorema de Kutta-Joukowski que dice que la elevación es igual a la densidad de flujo multiplicada por la circulación y la velocidad de transmisión libre.

Podemos, por lo tanto, combinar estos dos resultados diciendo que podemos modelar el elevador sobre una placa plana colocando un solo vórtice en el cuarto de cuerda de la placa plana (ya que aquí es donde la teoría dice que actúa la elevación neta). Todo esto nos da la imagen que se muestra a continuación.

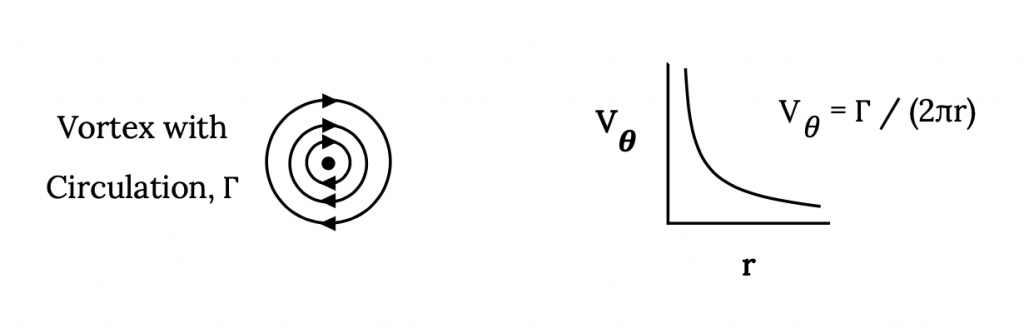
Básicamente, vamos a combinar estas dos ideas que describen la elevación seleccionando un lugar donde impondríamos una condición de no flujo a través de la placa plana que equiparará la elevación de los dos resultados teóricos. Para ello necesitamos saber algo sobre un vórtice que no hemos introducido previamente. Es decir, la velocidad encontrada en o introducida por un vórtice a diversas distancias de su centro. La teoría aerodinámica nos diría que la velocidad circular o tangencial en un vórtice varía inversamente con su radio y es función de la circulación, γ, en el vórtice. Teóricamente, un vórtice tiene una velocidad circunferencial infinita en su centro y esta velocidad se hace más pequeña a medida que nos alejamos del centro. Esto le dará

V _vórtice = γ/(2πr)

Al usar esta definición de la velocidad circunferencial en un vórtice, es convencional en el campo de la aerodinámica definir la dirección positiva para γ como en el sentido de las agujas del reloj. Esto desafía la práctica matemática convencional y hay que tener cuidado para ser consistente en el uso de la convención.

Esto se ilustra a continuación.

Volviendo a nuestra combinación de resultados de la teoría del perfil aerodinámico delgado y el Teorema de Kutta-Joukowski tenemos la siguiente tarea. Queremos encontrar algún punto en la placa plana donde el vórtice que hemos colocado en el cuarto de cuerda dará la cantidad justa de velocidad para contrarrestar el componente de la velocidad de transmisión libre normal a la placa de tal manera que nuestras dos miradas al coeficiente de elevación o elevación den las mismas respuestas. Una teoría, el Teorema de Kutta-Joukowski nos dice que L = ρV _∞ γ y la otra nos dice que el coeficiente de elevación C _L = 2πα.

Al darnos cuenta de que el levantamiento sobre una placa plana bidimensional es igual al coeficiente de elevación multiplicado por la presión dinámica, multiplicado por la longitud de la placa (un “área unidimensional”), podemos escribir:

L = ρ V _∞ γ = (2 πα) (½ ρ V _∞ ²) (c),

donde “c” es la cuerda (longitud) de la placa plana.

Se ve fácilmente que lo que aquí se busca es una relación entre el ángulo de ataque y la circulación en el vórtice. Estamos relacionando la realidad física de elevación creciente con ángulo de ataque con el modelo matemático que dice que la elevación aumenta con la circulación.

γ = πα V _∞ c.

Es esta relación la que usamos para crear nuestro “modelo de dorso del sobre” llamado Aproximación de Weissinger. Para ver esto necesitamos volver a mirar nuestra placa plana con el vórtice en el cuarto de cuerda y preguntarnos en qué radio del vórtice será suficiente la velocidad del vórtice para equilibrar el componente normal de la velocidad de transmisión libre.

Si observamos esta ilustración y usamos la última ecuación anterior para definir la circulación, γ, en términos de la velocidad de transmisión libre y el ángulo de ataque y luego equiparar la velocidad del vórtice y la componente normal de la velocidad de transmisión libre, encontramos

V _θ = γ/(2πr) = (πα V _∞ c)/(2πr) = V _{∞ n} = V _∞ sin (α) ≈ V ∞ α

o,

(α V _∞ c)/(2r) = V _∞ α, para pequeños ángulos de ataque.

El resultado final de esto es que la distancia, r, a la que debemos resolver para “no fluir a través de la placa plana” para hacer compatibles los dos modelos teóricos es:

r = c/ 2.

Debemos resolver para que no haya flujo a través de la placa en un punto tres cuartas partes del camino de regreso (en el punto de cuerda de tres cuartos) para hacer que esta “aproximación” funcione. Llamamos a este punto el “punto de control”.

Bien, entonces, ¿cuál es el problema? Hemos encontrado una nueva forma de obtener un resultado que ya conocemos y ¡es solo para un plato plano! ¿Cómo puede esta “aproximación” decirnos algo que no sepamos ya?

La razón por la que esto es tan útil es que podemos “construir” modelos aproximados de perfiles aerodinámicos combados o aleteados a partir de placas planas. Considera el caso simple de un perfil aerodinámico simétrico con un colgajo liso que ocupa el 20% final de su acorde. Podemos modelar esto como dos placas planas secuenciales con una placa plana de longitud del 80% de la cuerda aerodinámica y la otra 20% de la cuerda y podemos desviar el “flap” y ver qué le hace al coeficiente de sustentación. La forma en que se hace esto se ilustra en la siguiente figura:

En el caso anterior terminaremos con dos ecuaciones y dos incógnitas, los dos valores de circulación. Para obtener estas dos ecuaciones observamos los flujos normales a las dos placas en sus respectivos “puntos de control” que se han colocado en los ¾ puntos de cuerda en cada placa o panel. Veamos primero el punto de control en el primer panel.

Habrá tres velocidades que deben contabilizarse en este punto; la componente de la velocidad de transmisión libre normal al panel, la velocidad inducida por el vórtice en el primer panel y la velocidad inducida por el vórtice en el segundo panel. Podemos ver en la siguiente figura que la velocidad de transmisión libre se dirige hacia arriba mientras que las velocidades de los dos vórtices estarán en direcciones opuestas (que debido al primer vórtice es “abajo” y la velocidad del segundo vórtice es “arriba”, si asumimos que los vórtices son “positivos” o en sentido horario). Podemos dar cuenta de estas direcciones ya sea mediante la contabilidad mental y señalando que todas deben sumar a cero, o contabilizando concienzudamente los signos en las cantidades vectoriales, señalando que los radios (r ₁₁ y r ₂₁) tienen signos relacionados con su dirección.

Tenga en cuenta que la velocidad inducida en el punto de control 1 por el vórtice en el panel 2 no es exactamente perpendicular al panel 1. Podríamos ser muy precisos y usar un poco de trigonometría para averiguar el ángulo exacto y contabilizarlo para encontrar el verdadero componente normal o simplemente podríamos suponer que está lo suficientemente cerca de lo normal como para ignorar el ángulo. Ya que este es un método aproximado de todos modos, excepto en el caso de ángulos muy grandes (digamos diez grados o más) usualmente ignoraremos el error. Haciendo esto, podemos escribir una ecuación sumando los dos componentes de vórtice de velocidad y equiparando su suma con el componente de corriente libre.

V ₁₁ + V ₂₁ = V _{∞ n 1} = V _∞ sin (α ₁ ) ≈ V _∞ α ₁

donde

V ₁₁ = γ ₁/(2πr ₁₁)

V ₂₁ = γ/(2πr ₂₁)

y donde

r ₁₁ = 0.4c

r ₂₁ ≈ — 0.25c

Ahora bien, haríamos exactamente lo mismo en el punto de control del segundo panel.

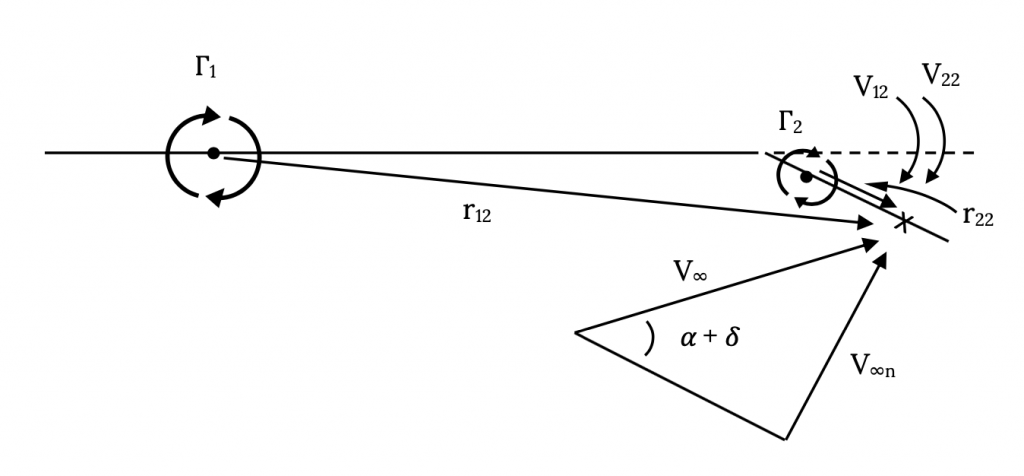
Aquí nuestra ecuación será similar a la del punto de control en el panel uno excepto que probablemente tendremos que tener en cuenta el hecho de que el ángulo de deflexión del flap probablemente será demasiado grande para simplemente ignorarlo al encontrar el componente normal de la velocidad de transmisión libre.

V ₁₂ + V ₂₂ = V _{∞ n2} = V _∞ sin (α ₂) = V _∞ sin (α + δ)

donde

δ = ángulo de deflexión del flap

V ₁₂ = γ ₁/(2πr ₁₂)

V ₂₂ = γ ₂/(2πr ₂₂)

r ₁₂ ≈ 0.75c

r ₂₂ = 0.1c

Entonces resolveríamos simultáneamente estas dos ecuaciones, teniendo cada una dos incógnitas (γ ₁ y γ ₂) para esos valores desconocidos. Entonces usaríamos esos dos valores de circulación para encontrar el coeficiente de elevación total y elevación donde el levantamiento simplemente se encontraría del Teorema de Kutta-Joukowski, sumando los levantamientos en cada panel.

L = σ ρ V _∞ γ = ρV _∞ [γ ₁ + γ ₂]

y el coeficiente de elevación sería

C _L = L/(½ ρ V _∞ ² c) = 2 [γ ₁ + γ ₂]/(V _∞ c)

Ejercicio:

Resuelve el problema anterior para una velocidad de transmisión libre de 100 mph, una desviación de colgajo de 20 grados y una cuerda de ala de 5 pies a nivel del mar en un ángulo de ataque de 5 grados. ¿Cómo se compara este coeficiente de sustentación con el de un perfil aerodinámico simétrico en el mismo ángulo de ataque?

Tenga en cuenta que en la solución aproximada anterior para un perfil aerodinámico aleteado y simétrico tenemos una “distribución de elevación” muy cruda sobre la cuerda aerodinámica, es decir, sabemos la forma en que se puede dividir la elevación para actuar en las dos ubicaciones anteriores. Si resolviéramos esto para varios ángulos de ataque diferentes encontraríamos que los valores relativos de las dos resistencias de vórtice (circulaciones) cambiarían. Si miramos de cerca esto encontraríamos que, a diferencia del perfil aerodinámico simétrico donde siempre se puede decir que el levantamiento actúa en el cuarto de cuerda del perfil aerodinámico, para el perfil aerodinámico combado el punto donde actuará el elevador (centro de elevación o centro de presión) se moverá con ángulo de ataque y será una función de camber. Si quisiéramos encontrar esto con mayor precisión podríamos usar más paneles y más vórtices y puntos de control (junto con más ecuaciones). Para el ejemplo anterior podría ser natural simplemente dividir el perfil aerodinámico en cinco paneles de igual longitud, cada 20% del acorde original, luciendo algo así como el boceto de abajo.

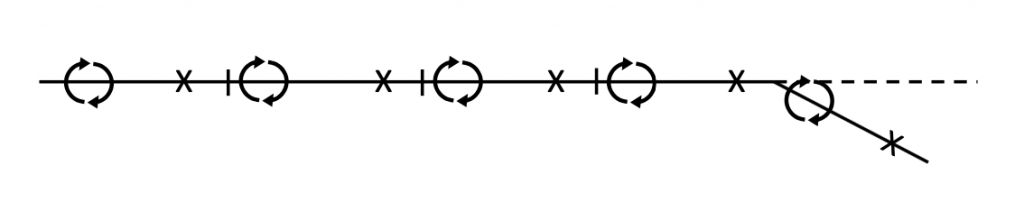
Y, no es demasiado difícil imaginar extender este método a un perfil aerodinámico verdaderamente arqueado como se muestra en la Figura 3.12.

Esta simple aproximación basada en los resultados del comportamiento aerodinámico de placa plana se ha estirado, de esta manera, en una verdadera “solución numérica” para un perfil aerodinámico de cualquier forma de curvatura con tantos paneles como se desee utilizar. Podemos usarlo para encontrar el coeficiente de elevación total o elevación para un perfil aerodinámico con cualquier forma de curvatura y también para encontrar la forma en que la elevación se distribuye sobre la cuerda del perfil aerodinámico.

Otra cosa que podemos encontrar de esto es el “momento de pitcheo” del perfil aerodinámico, su tendencia a girar nariz hacia arriba o nariz hacia abajo sobre cualquier punto de referencia deseado en el acorde. El momento de cabeceo se acaba de encontrar tomando cada fuerza de “elevación” encontrada de las circulaciones individuales y multiplicándola por la distancia o “brazo de momento” entre ese vórtice y el punto de referencia deseado. Si, por ejemplo, queremos usar el borde de ataque del ala como nuestra referencia de momento (una elección común en cálculos teóricos o numéricos) solo necesitamos tomar cada valor de gamma multiplicado por la distancia desde el borde de ataque del perfil aerodinámico y ese vórtice y sumarlos para obtener el momento de cabeceo total sobre el avance borde.

Para el perfil aerodinámico simétrico (placa plana) donde el centro de elevación está siempre en el cuarto de cuerda, este momento de cabeceo alrededor del borde de ataque siempre será el levantamiento multiplicado por la distancia de cuarto de cuerda. El coeficiente de momento de cabeceo para este caso sería la elevación multiplicada por la distancia de cuarto de cuerda, dividido por la presión dinámica multiplicada por el cuadrado de la cuerda. ¿Hacer un cálculo rápido para ver qué sería esto?

3.3 Momento de pitcheo

Mientras estamos hablando de encontrar el momento de pitcheo echemos un vistazo a algunos casos especiales. El momento de pitcheo se puede calcular o medir sobre cualquier punto que queramos utilizar. A menudo, en cálculos analíticos o numéricos es conveniente encontrar el momento de cabeceo alrededor del borde de ataque del ala. Por otro lado, en las pruebas de túnel de viento podría ser más conveniente medir el momento en algún momento entre 20% y 50% hacia atrás desde el borde de ataque debido a la facilidad de unir allí el sistema de equilibrio de fuerza y momento.

En el Capítulo Uno mencionamos dos localizaciones significativas donde el momento de pitcheo o su coeficiente tiene significados especiales. Estos fueron el centro de presión (centro de elevación) y el centro aerodinámico; puntos donde el coeficiente de momento es cero o donde permanece constante a medida que cambian el coeficiente de sustentación y el ángulo de ataque. Según la teoría del perfil aerodinámico delgado, estos son coincidentes en el cuarto de cuerda para un perfil aerodinámico simétrico pero para el perfil aerodinámico combado, el centro de presión generalmente se moverá a medida que cambia el ángulo de ataque mientras que el centro aerodinámico permanece en el cuarto de cuerda. Podemos verificar que este resultado teórico es una coincidencia bastante buena para la realidad al observar los gráficos de datos aerodinámicos presentados en el Apéndice A (discutido anteriormente en el Capítulo Uno). A menudo, estas gráficas presentan dos gráficas para el coeficiente de momento de cabeceo con la primera (a la izquierda en la mayoría de las figuras) una gráfica de C _Mc/4 (el coeficiente de momento en el cuarto de cuerda) y la otra gráfica (generalmente a la derecha) de C _MAC (coeficiente de momento en el centro aerodinámico). En las parcelas del Apéndice A para perfiles arqueados se puede observar que C _Mc/4 es distinto de cero en valor y cambia con el ángulo de ataque mientras que C _MAC es relativamente constante antes del inicio de la calada. En las gráficas de datos simétricos de superficie aerodinámica, ambas cantidades son cero (o cercanas a cero) en valor y constantes antes del atasco. En el calado, la elevación o distribución de presión sobre el perfil aerodinámico está cambiando drásticamente a medida que el flujo comienza a separarse en porciones progresivamente más grandes del perfil aerodinámico y las aproximaciones de la teoría del perfil aerodinámico delgado están lejos de ser válidas.

Como se señaló en la sección anterior, el momento de cabeceo y el coeficiente de momento se pueden calcular junto con la elevación cuando se utiliza la Aproximación de Weissinger. Para encontrar la ubicación del centro de presión solo necesitamos usar la definición de ese punto como siendo donde el momento es cero para encontrar su ubicación. Con base en la siguiente ilustración, podemos suponer que el centro de presión se ubica en algún punto X _cp y sumar los momentos alrededor de ese punto desconocido debido a las diversas fuerzas de elevación inducidas por la circulación para igualar a cero.

ρV _∞ [γ ₁ (x ₁ -x _cp) + γ ₂ (x ₂ -x _cp) + • • • • + γ _n (x _n -x _cp)] = 0

En esta ecuación x ₁, x ₂, a través de x _n están las ubicaciones a lo largo de la cuerda de los diversos vórtices (cada uno en el cuarto de cuerda de su panel) y x _cp es la ubicación desconocida del centro de presión. Esto se resuelve para x _cp, la ubicación del centro de presión. Tenga en cuenta que para un perfil aerodinámico simétrico (placa plana) esta posición no debe cambiar con el ángulo de ataque mientras que para un perfil aerodinámico _{curvado x cp} será diferente para cada ángulo de ataque.

De manera similar, pero un poco más complicada, pudimos encontrar la ubicación del centro aerodinámico a partir de los resultados de levantamiento de aproximación de Weissinger. Esto implicaría encontrar el punto donde dC _M /dC _L = 0. Dejaremos este cálculo para un texto o curso en aerodinámica.

3.4 Alas (Aerodinámica 3-D)

Como se señaló en el Capítulo Uno, la principal diferencia entre el flujo bidimensional alrededor de un perfil aerodinámico y el flujo tridimensional alrededor de un ala es el flujo alrededor de la punta del ala desde la parte inferior hasta la parte superior del ala. Esto da como resultado varias cosas:

• Un flujo hacia afuera a lo largo de la parte inferior del ala cerca de la punta.
• Un flujo hacia adentro a lo largo de la parte superior del ala cerca de la punta.
• Un sistema de vórtice de arrastre.
• Un “downwash” en el ala causado por el sistema de vórtice de arrastre.
• Un “arrastre inducido” causado por el downwash.

Este flujo de vórtice fuera de cada punta de ala es un flujo muy real que se puede ver en el túnel de viento ya sea con humo o simplemente pegando una cuerda en el flujo detrás de la punta del ala. También se puede ver en aviones en vuelo cuando las condiciones atmosféricas son las adecuadas. Si hay suficiente humedad en el aire en forma de humedad relativa alta o debido a que el vapor de agua en el escape del motor a reacción es arrastrado hacia los vórtices posteriores, la baja presión en el núcleo del vórtice hará que el vapor de agua se condense, haciéndolo visible como un par de “tornados blancos” que se arrastran detrás de cada uno punta de ala. Es interesante observar estos cuando son visibles desde jets de alto vuelo y ver exactamente cuánto tiempo persisten. Pueden existir por muchas millas detrás de la aeronave generadora, ilustrando tanto la cantidad de energía en los vórtices como el peligro para otras aeronaves que puedan encontrarlos.

Estos “vórtices finales” son el factor clave para tratar de crear cualquier tipo de modelo matemático del flujo 3-D alrededor y detrás de un ala real. En esencia, esto se hace doblando los vórtices que se utilizaron para modelar el flujo sobre un perfil aerodinámico en un ángulo de 90 grados y permitiéndoles caminar detrás del ala. Y, como sabemos que el levantamiento del ala varía a lo largo de su envergadura y no solo permanece igual hasta la punta del ala, permitimos que los vórtices giren a la derecha o a la izquierda y salgan del ala a lo largo de su envergadura. Esto produce lo que se llama un “sistema de vórtice de herradura”.

Si bien esta derivación teórica está más allá del alcance pretendido de este material, su esencia se encuentra en los siguientes hechos o supuestos:

• Se supone que la circulación total en el ala varía a lo largo del tramo y va a cero en las puntas del ala.
• Los “vórtices posteriores” inducen un flujo descendente o “downwash” que crea una velocidad descendente pequeña pero significativa en el ala misma. (En realidad, esta es una manera de dar cuenta del impulso descendente del flujo que resulta de la fuerza de elevación. Esto también se podría encontrar a partir de la ecuación de momentum si tuviéramos suficiente información.)
• De la misma manera que la interacción de la velocidad de transmisión libre, V _∞, con las circulaciones de vórtice en el ala da como resultado sustentación (Teorema de Kutta-Joukowski), la interacción de esta velocidad de “downwash” con las circulaciones de vórtice provoca un arrastre. A esto lo llamamos el “arrastre inducido”.

Usando este modelo de vórtice de herradura y asumiendo que todos los vórtices en el ala están agrupados en un solo núcleo similar a una cuerda en el cuarto de cuerda del ala y también asumiendo que el acorde del cuarto del ala no está barrido, se puede usar un método denominado “teoría de líneas de elevación” para encontrar el variación de elevación a lo largo del tramo y la resistencia inducida para cualquier ala no barrida de relación de aspecto moderada a alta. Cualquier buen texto sobre aerodinámica tendrá un desarrollo completo de este enfoque de la aerodinámica 3-D y presentará sus resultados.

Uno de los resultados del uso de la teoría de líneas de elevación será un caso “óptimo”, es decir, una distribución de sustentación a lo largo de la envergadura en el ala donde la resistencia inducida es mínima. Esto resulta ser una solución donde la distribución de la circulación en el sentido de la envergadura sobre el ala es elíptica en forma y forma matemática. Esta solución especial dará la ecuación para el coeficiente de arrastre inducido que ya hemos citado en el Capítulo Uno,

C _Di = C _L ²/(πAR)

donde “AR” es la relación de aspecto,

AR = b ² /S = b/ c _promedio.

La forma más general (no óptima) de esta ecuación para el coeficiente de arrastre inducido incluye otro término, “e”, conocido como factor de eficiencia de Oswald, que explica las variaciones de circulación no elípticas en el sentido de la envergadura.

C _Di = C _L ²/(π AR e)

Este factor de eficiencia de Oswald se puede calcular a partir de la teoría de líneas de elevación en forma de serie de Fourier.

Si bien no es el propósito de este texto entrar en muchos detalles examinando la teoría de la línea de elevación, me gustaría ver brevemente lo que dice sobre la elevación para el caso especial, mínimo arrastre, de la distribución de elevación elíptica porque a menudo usamos este caso especial para echar un primer vistazo a las influencias del ala diseño sobre aerodinámica y rendimiento. Sin derivarlos, simplemente veremos algunos de los resultados más importantes de la teoría de líneas de elevación relacionadas con la elevación:

L = (π/ 4) ρ V _∞ Bγ _centro

donde

b = envergadura del ala

γ _centro = el valor de la circulación en el centro de la envergadura del ala

y

γ _centro = (2C _L V _∞ S)/(πb)

Tenga en cuenta que esto hace que el coeficiente de elevación sea una función de la relación de aspecto:

C _L = L/(½ ρ V _∞ ² S) = (π Bγ _centro)/(2V _∞ S) = (π AR γ _centro)/(2Bv _∞)

Esto dice que para cualquier ángulo de ataque dado (o valor de circulación ya que el _centro γ debe aumentar con el ángulo de ataque) un diseño de ala de mayor relación de aspecto dará un coeficiente de sustentación mayor que un ala AR baja.

Si trazamos coeficiente de elevación versus ángulo de ataque para dos alas de diferente relación de aspecto, encontraríamos que la “pendiente” de la curva de elevación disminuiría con la disminución de la relación de aspecto. El valor máximo de la pendiente es 2-pi, el valor de superficie aerodinámica bidimensional, equivalente a un ala de relación de aspecto infinita.

Otra forma de ver este mismo efecto es mirar el ángulo de ataque en el que se deben volar dos alas de diferentes relaciones de aspecto para obtener el mismo valor de coeficiente de sustentación:

α ₂ = α ₁ + (C _L /π) [(1/AR ₂) — (1/AR ₁)]

Las relaciones anteriores nos proporcionan herramientas valiosas para examinar los efectos de variables de diseño como la relación de aspecto del ala sobre la aerodinámica y el rendimiento de una aeronave. Si deseamos usar un ala de relación de aspecto moderada en lugar de un diseño de relación de aspecto alta por, digamos, razones estructurales o por una dinámica de balanceo mejorada, podemos ver qué penalización pagaremos. A menudo, la penalización puede no ser tan grande como podríamos creer al principio con base en nuestro conocimiento básico que una relación de aspecto alta suele ser deseable.

Estas ecuaciones son, como se mencionó anteriormente, para el caso ideal, la distribución de elevación elíptica o el caso de arrastre inducido mínimo. Sin embargo, pueden darnos una idea bastante buena de cómo cosas como los cambios en la relación de aspecto influirán en el rendimiento de cualquier ala tridimensional.

Una última cosa que me gustaría mencionar en este capítulo se refiere a los supuestos mencionados anteriormente para la teoría de la línea de elevación. Se observó que esta teoría supone que el cuarto de cuerda del ala está sin barrer. Otra suposición inherente a la teoría de líneas de elevación de uso que no se mencionó es que la teoría no es muy buena para alas de baja relación de aspecto. Incluso con estas dos limitaciones importantes, la teoría de la línea de elevación nos da algunas ideas importantes sobre la aerodinámica 3D. Pero, ¿qué haríamos si estamos viendo un ala con barrido o baja relación de aspecto?

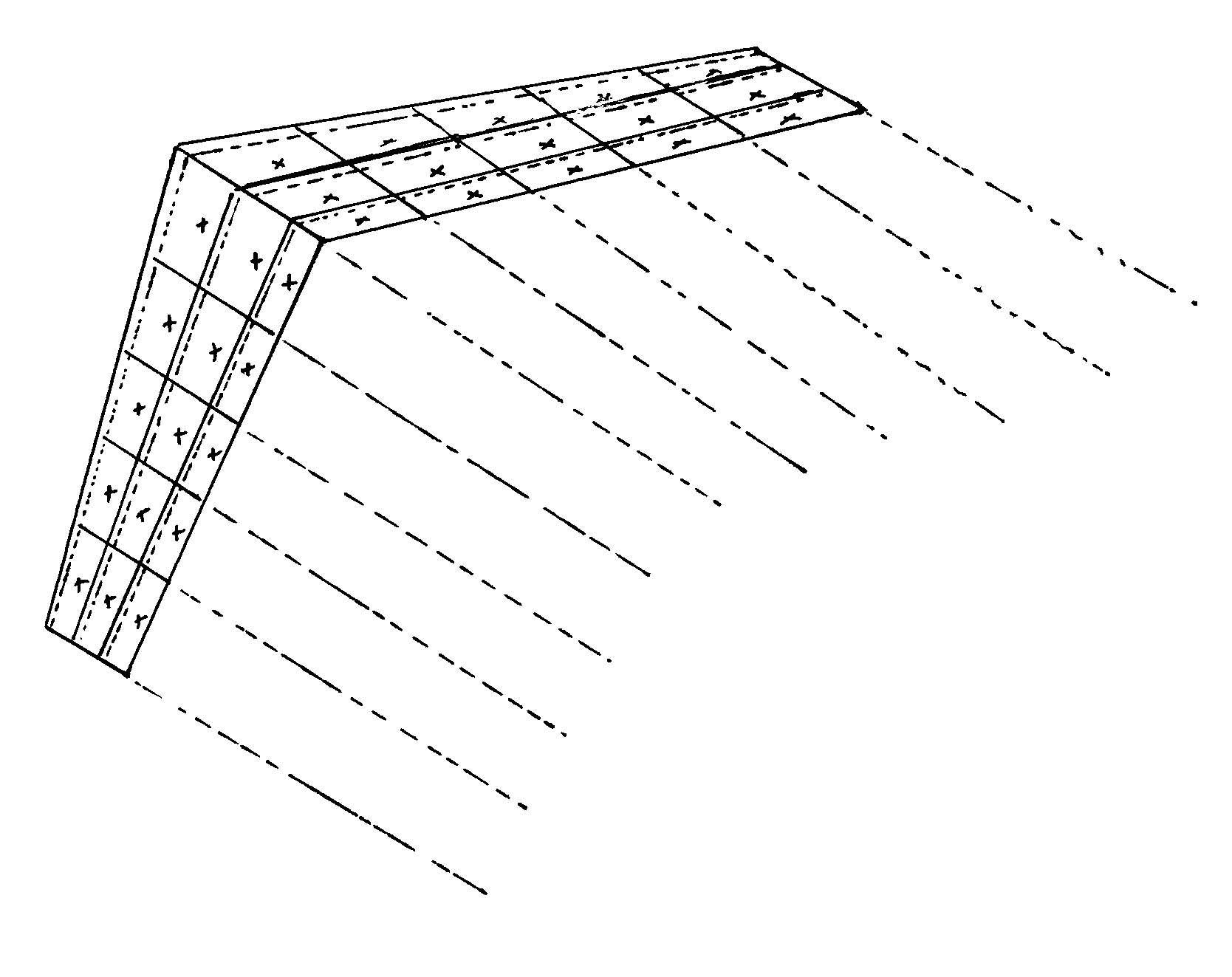
Para alas barridas, alas con baja relación de aspecto, o cualquier otra ala más allá de los límites de los supuestos de la teoría de líneas de elevación, el enfoque habitual es ir a alguna variación de lo que se llama teoría de “celosía de vórtice”. El ala (o incluso todo el avión) se divide en paneles y se coloca un solo vórtice de “herradura” en el cuarto de cuerda de cada panel en lo que es esencialmente una versión tridimensional de la Aproximación de Weissinger. Si el ala se rompe en N paneles, hay N vórtices de herradura y estos deben resolverse estableciendo N ecuaciones. Las ecuaciones se resuelven para la condición de no flujo a través de los paneles (la misma idea que con la Aproximación de Weissinger) en el tramo central de la cuerda de tres cuartos del panel. Esta solución es tres veces más compleja que el método 2-D Weissinger porque cada vórtice de herradura tiene tres segmentos (uno que abarca el cuarto de cuerda del panel y los otros dos actúan como “vórtices finales” desde el primer vórtice en los bordes del panel. Al igual que en el método 2-D, las ecuaciones resueltas en los “puntos de control” tuvieron que dar cuenta de todas las velocidades inducidas por todos los vórtices en el plano aerodinámico así como la velocidad de la corriente libre, en la aproximación de la red de vórtice 3-D la ecuación en cada punto de control de panel debe dar cuenta de las velocidades inducidas por todos tres segmentos de vórtice de todos los paneles N, así como para la velocidad de transmisión libre.

Los métodos de celosía de vórtice pueden ser intimidantes al principio; sin embargo, al igual que la aproximación de Weissinger en 2-D, simplemente usan ecuaciones N para resolver N incógnitas donde lo desconocido es la fuerza del vórtice de herradura en cada panel 3-D. Todo lo demás se reduce a modelar la geometría del ala 3-D. El resultado será el vector de velocidad 3-D paralelo a cada punto de control del panel y estos pueden ser utilizados para encontrar las presiones y fuerzas y momentos alrededor del ala.

3.5 Aerodinámica Vortex: Winglets

Veremos un tema final en este capítulo, el de la “aerodinámica vorticial”. Como ya hemos visto, los vórtices juegan un papel importante en la forma en que modelizamos matemáticamente el perfil aerodinámico y la aerodinámica del ala. Y, como hemos visto en el caso de los flujos tridimensionales alrededor de las puntas de las alas, los vórtices en realidad juegan un papel muy real en la creación de cosas como lift and drag y los modelos matemáticos que construimos para explicar la aerodinámica también hacen un excelente trabajo de modelar estos vórtices reales y sus efectos.

Hay muchas situaciones además de los vórtices de la punta del ala donde estos flujos parecidos a tornados existen en la “vida real” y juegan un papel importante en la creación de fuerzas y momentos en aviones y alas. Uno de los trabajos del aerodinamista es modelar correctamente estos vórtices y sus efectos y otro trabajo puede ser determinar si hay formas de utilizar estos flujos arremolinados para nuestra ventaja de manera que mejoren la aerodinámica y el rendimiento de vuelo de un avión.

Analizaremos dos casos muy importantes e interesantes donde la aerodinámica de vórtices juega un papel importante. Estas son en el uso de “winglets” y “extensiones de borde de ataque” (a veces conocidas como “strakes” o “guantes de ala”).

El winglet es, a estas alturas, una adición bastante conocida a las puntas de las alas de muchos aviones pero su propósito es ampliamente incomprendido. Durante muchos, muchos años ingenieros y científicos probaron muchos enfoques que podrían reducir la fuerza o los efectos de los vórtices de la punta del ala o que los eliminarían por completo. Desafortunadamente, las leyes de la Física son difíciles de superar, y esta energía rotacional que cuantificamos como “circulación” tiene que ir a algún lugar en la punta del ala y realmente no hay forma de eliminarla en vuelo más que dejar que se disipe lentamente como un par de vórtices que se arrastran en algún lugar de la atmósfera aguas abajo de la aeronave. Podemos poner grandes placas en la punta del ala o crear formas interesantes en la punta del ala en intentos de eliminar o acelerar la disipación de los vórtices de arrastre pero el efecto habitual es simplemente crear una circular ligeramente diferente de distribución de velocidad tangencial dentro del vórtice mismo, un patrón que puede o no hacer que los vórtices sean menos peligrosos para los aviones de arrastre y pueden o no resultar en una reducción en la resistencia inducida por el ala. Por lo general, los efectos de tales “arreglos” son mayores en la imaginación de su inventor que en la vida real.

El winglet, más propiamente conocido como el winglet Whitcomb después de su inventor, Richard Whitcomb de Nasa-langley, no está diseñado, contrariamente a la sabiduría convencional, para eliminar los vórtices de la punta del ala. En lugar de tratar de eliminar algo que no se puede eliminar sin eliminar la elevación del ala, Whitcomb decidió usar los vórtices de arrastre para crear un efecto positivo. En una conversación con el autor, el señor Whitcomb explicó que veía que las aletas funcionaban de manera muy parecida a la quilla de un velero que está navegando o “virando” al viento. Una quilla de velero es una especie de ala en el fondo del barco, y cuando un velero navega hacia el viento, la fuerza de avance no viene de la vela en absoluto. En cambio, la vela está creando una fuerza lateral que empuja la quilla a través del agua de tal manera que se crea una fuerza dirigida hacia adelante. La fuerza hacia adelante que empuja un velero hacia el viento viene de un ala pequeña en el agua más que del ala grande que llamamos vela.

Al crear el winglet, Richard Whitcomb razonó que si el ala grande de un velero pudiera crear un flujo sobre un ala más pequeña (la quilla) que produciría un empuje, debería haber una manera de tomar el flujo creado por un ala grande en un avión (el vórtice de punta) y usarlo para crear un empuje en un ala más pequeña. Esa ala más pequeña terminó siendo la winglet. El winglet Whitcomb se coloca en lo que parecería ser un ángulo de ataque negativo en la punta del ala de tal manera que la combinación de la velocidad de transmisión libre y las velocidades de flujo del vórtice de la punta del ala crea una “elevación” en la aleta que en realidad apunta hacia adelante, dando un empuje. Y resulta que este empuje es lo suficientemente significativo como para mejorar las relaciones de elevación-resistencia en un ala en un quince a veinte por ciento. Esto puede resultar en mejoras muy significativas en el rendimiento y la economía de los vuelos de los aviones.

3.6 Aerodinámica Vortex: Vórtice de borde de ataque

El segundo tipo de vórtice real que queremos examinar muy brevemente es el “vórtice de borde de ataque”. Tal vórtice se forma cuando un ala es barrida a ángulos de aproximadamente 50 grados o más. Estos vórtices, ilustrados en la figura 3.18 a continuación, resultan de una combinación de un flujo tridimensional en el ala y del flujo normal alrededor del borde de ataque del ala. Este flujo combinado realmente se separa de la superficie del ala en el borde de ataque pero, debido al flujo rotacional en el vórtice, se vuelve a unir a la superficie del ala de tal manera que el ala no se detenga en el ángulo de ataque habitual de quince a veinte grados, sino que ha unido flujo y levanta hasta ángulos mucho mayores de ataque.

Las alas suelen ser barridas para retrasar el inicio del ascenso de arrastre transónico cerca de Mach One y para reducir la magnitud de esa subida de arrastre. Por otro lado, las alas barridas producen menos sustentación convencional en un ángulo de ataque dado que un ala no barrida, de la misma manera que las alas de menor relación de aspecto dan menos sustentación en un ángulo de ataque dado que las alas de alta relación de aspecto. El efecto del vórtice del borde de ataque es doble. Primero, al mantener el flujo unido a ángulos de ataque mucho más altos de lo normal, permiten que el ala produzca sustentación en estos ángulos de ataque más altos de lo normal. A esta mayor ventaja del ángulo de ataque se agrega una elevación adicional, llamada “elevación de vórtice” que se crea por la presión muy baja en el núcleo del vórtice. Desafortunadamente, esta baja presión en el vórtice también agrega algo de resistencia, pero el efecto neto puede ser muy útil para permitir que los aviones que necesitan alas muy barridas operen eficientemente a velocidades transónicas y supersónicas para obtener aún el sustento que necesitan a velocidades subsónicas más bajas. También pueden permitir que los aviones de combate militares “vuelen” a actitudes muy inusuales (ángulos de ataque) que pueden ser muy útiles en el combate aire-aire.

A veces queremos crear esta misma capacidad en alas que no son barridas tanto. Esto se puede hacer agregando extensiones de borde de ataque altamente barridas o strakes. Estas bandas crean sus propios vórtices de borde de ataque que continúan sobre el ala detrás de ellos, dando muchos de los beneficios mencionados anteriormente y permitiendo que los aviones con barrido de ala relativamente bajo vuelen a ángulos de ataque mucho más altos que los normales cuando sea necesario. Un avión que hace buen uso de este efecto es el F-18 de la Marina. Sus tiras muy largas y muy barridas le permiten operar en los ángulos altos o de ataque y bajas velocidades necesarias para aterrizar y despegar en portaaviones a la vez que le dan una gran maniobrabilidad de ángulo de ataque muy útil que es muy útil en combate de caza.

Como se mencionó al inicio de este capítulo, la cobertura en el capítulo no es realmente necesaria para poder entender o trabajar con el material sobre el rendimiento de la aeronave que seguirá. Se ha incluido simplemente para rellenar algunos de los espacios en blanco que podrían haberse dejado abiertos en el Capítulo Uno. Por otro lado, se puede utilizar para potenciar la siguiente cobertura de desempeño de la aeronave y para relacionarla mejor con algunos de los conceptos básicos en aerodinámica.

Testo 3

1. El Airbus 380-100 está diseñado para viajar a 35.000 pies con un número Mach de 0.85. Su peso en crucero es de aproximadamente un millón de libras. Tiene un área de ala de 9100 pies ² y una envergadura de ala de 262 pies. Suponiendo que la elevación es igual al peso y el empuje es igual a arrastre y que en crucero a esta altitud se necesitan 50,000 libras de empuje, encuentre:

a. La velocidad de vuelo en millas por hora y en nudos

b. El coeficiente de elevación

c. El coeficiente de arrastre

d. Su número de Reynolds basado en acorde medio

2. Si un avión está despegando simplemente acelerando por la pista hasta que tenga la velocidad suficiente para que su sustentación iguale su peso y su ala esté en un ángulo de ataque de cinco grados, qué velocidades se requieren para el despegue a nivel del mar y a 5000 sentir altitud asumiendo que su ala tiene una pendiente de curva de sustentación (dC _L /dα) de 0.08 por grado y un ángulo de ataque de elevación cero (α _L0) de menos un grado? También encuentra la velocidad aérea indicada en ambas altitudes. Supongamos que el avión pesa 11,250 libras y tiene un área de ala de 150 pies ².

Nota: Normalmente la mayoría de las aeronaves acelerarían a un bajo valor de coeficiente de sustentación y luego “rotarían” para aumentar su ángulo de ataque a un valor que le daría elevación + peso a la velocidad de despegue definida. Esto permitiría el despegue en una distancia más corta que el método anterior. Veremos esto en detalle más adelante en el curso.