4: Rendimiento en vuelo recto y nivelado
( \newcommand{\kernel}{\mathrm{null}\,}\)
Introducción
Ahora que hemos examinado los orígenes de las fuerzas que actúan sobre una aeronave en la atmósfera, necesitamos comenzar a examinar la forma en que estas fuerzas interactúan para determinar el rendimiento del vehículo. Sabemos que las fuerzas dependen de cosas como la presión atmosférica, densidad, temperatura y viscosidad en combinaciones que se convierten en “parámetros de similitud” como el número de Reynolds y el número de Mach. También sabemos que estos parámetros variarán como funciones de altitud dentro de la atmósfera y contamos con un modelo de atmósfera estándar para describir esas variaciones. También es obvio que las fuerzas en una aeronave serán funciones de velocidad y que esto forma parte tanto del número de Reynolds como del número de Mach.
Muchas de las preguntas que tendremos sobre el rendimiento de las aeronaves están relacionadas con la velocidad. ¿Qué tan rápido puede volar el avión o qué tan lento puede ir? ¿Qué tan rápido puede subir el avión? ¿Qué velocidad es necesaria para despegar de la pista?
En la sección anterior sobre análisis dimensional y similitud de flujo encontramos que las fuerzas en una aeronave no son funciones de velocidad solo sino de una combinación de velocidad y densidad que actúa como una presión que llamamos presión dinámica. Esta combinación aparece como uno de los tres términos en la ecuación de Bernoulli
P+12ρV2=P0
que se puede reorganizar para resolver la velocidad
V=√2(P0−P)/ρ
En el capítulo dos aprendimos cómo se puede usar un tubo PITOT estático para medir la diferencia entre la presión estática y la presión total para encontrar la velocidad del aire si la densidad es conocida o asumida. Se discutió tanto la velocidad aerodinámica equivalente al nivel del mar que asume la densidad estándar del nivel del mar para encontrar velocidad como la verdadera velocidad aérea que utiliza la densidad atmosférica real. Al tratar con aeronaves es costumbre referirse a la velocidad aerodinámica equivalente al nivel del mar como la velocidad aérea indicada si se puede descuidar algún error de calibración o colocación del instrumento. En este texto vamos a suponer que efectivamente se pueden descuidar tales errores y el término velocidad aérea indicada se utilizará indistintamente con velocidad aerodinámica equivalente a nivel del mar.
VIND=Ve=VSL=√2(P0−P)ρSL
Cabe señalar que las ecuaciones anteriores asumen un flujo incompresible y no son precisas a velocidades donde los efectos de compresibilidad son significativos. En teoría, los efectos de compresibilidad deben considerarse en números Mach superiores a 0.3; sin embargo, en realidad, las ecuaciones anteriores pueden ser utilizadas sin error significativo para números Mach de 0.6 a 0.7.
El sistema de indicación de velocidad aérea de las aeronaves de alta velocidad debe ser calibrado sobre una base más complicada que incluya la velocidad del sonido:
VIND=√2a2SLγ−1[(P0−PρSL+1)γ−1γ−1]
dondeasl = velocidad del sonido al nivel del mar y ρ SL = presión al nivel del mar. Gamma es la relación de calores específicos (Cp/Cv) para el aire.
Los aviones de muy alta velocidad también estarán equipados con un indicador Mach ya que el número Mach es una medida más relevante de la velocidad de la aeronave a y por encima de la velocidad del sonido.
En el resto de este texto se asumirá que los efectos de compresibilidad son insignificantes y la forma incompresible de las ecuaciones puede ser utilizada para todos los cálculos relacionados con la velocidad. La velocidad aérea indicada (la velocidad que sería leída por el piloto de la aeronave desde el indicador de velocidad aérea) se asumirá igual a la velocidad aerodinámica equivalente al nivel del mar. Así, la verdadera velocidad del aire se puede encontrar corrigiendo la diferencia en el nivel del mar y la densidad real. La corrección se basa en el conocimiento de que la presión dinámica relevante a altitud será igual a la presión dinámica a nivel del mar como se encuentra a partir de la velocidad aerodinámica equivalente a nivel del mar:
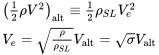
Un resultado importante de esta equivalencia es que, dado que las fuerzas sobre la aeronave dependen de la presión dinámica más que de la velocidad del aire, si conocemos las condiciones de vuelo equivalentes a nivel del mar y calculamos las fuerzas a partir de esas condiciones, esas fuerzas (y de ahí el rendimiento del avión) serán correctamente pronosticado con base en las condiciones indicadas de velocidad aérea y nivel del mar. Esto también significa que el piloto del avión no necesita convertir continuamente las lecturas de velocidad aerodinámica indicadas a velocidades aéreas verdaderas para medir el rendimiento de la aeronave. La aeronave siempre se comportará de la misma manera a la misma velocidad aérea indicada independientemente de la altitud (dentro del supuesto de flujo incompresible). ¡Esto es especialmente agradable de saber en situaciones de despegue y aterrizaje!
4.1 Equilibrio estático de fuerzas
Muchos de los parámetros de desempeño importantes de una aeronave se pueden determinar utilizando únicamente la estática; es decir, asumiendo el vuelo en una condición de equilibrio tal que no haya aceleraciones. Esto significa que el vuelo se encuentra a altitud constante sin aceleración ni desaceleración. Esto da la disposición general de las fuerzas que se muestran a continuación.
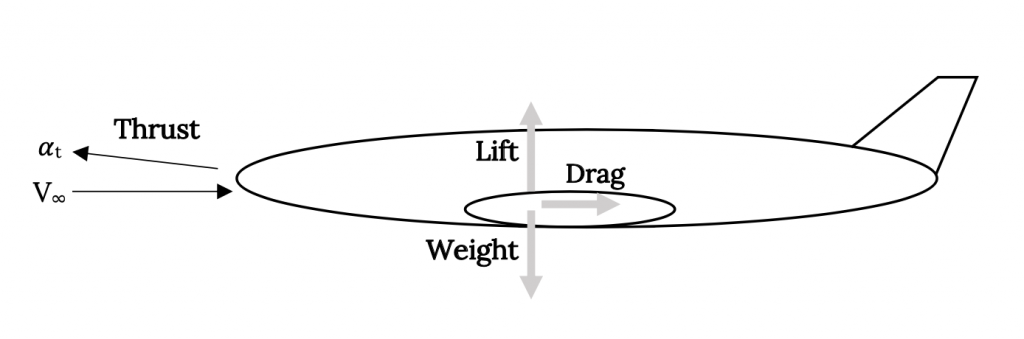
En este texto consideraremos el caso más simple donde el empuje se alinea con el vector de velocidad de la aeronave. También asumiremos normalmente que el vector de velocidad está alineado con la dirección de vuelo o trayectoria de vuelo. Para este caso más básico las ecuaciones de movimiento se convierten en:
T — D = 0
L — W = 0
Tenga en cuenta que esto es consistente con la definición de sustentación y arrastre como perpendicular y paralelo al vector de velocidad o viento relativo.
Ahora hacemos una suposición simple pero muy básica de que en vuelo recto y nivelado el levantamiento es igual al peso,
L = W
Utilizaremos esto tan a menudo que será fácil olvidar que sí asume que el vuelo es efectivamente recto y nivelado. Posteriormente haremos trampa un poco y lo usaremos en subidas y deslizamientos poco profundos, cubriéndonos asumiendo un vuelo “cuasi-recto y nivelado”. En la parte final de este texto finalmente iremos más allá de esta suposición cuando consideremos girar vuelo.
Usando la definición del coeficiente de elevación
CL=L12ρV2∞S
y la suposición de que la elevación equivale al peso, la velocidad en vuelo recto y nivelado se convierte en:
V=√2WρSCL
El empuje necesario para mantener esta velocidad en vuelo recto y nivelado también es una función del peso de la aeronave. Desde T = D y L = W podemos escribir
D/L = T/W
o
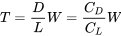
Por lo tanto, para vuelo recto y nivelado encontramos esta relación entre empuje y peso:
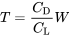
Las ecuaciones anteriores para el empuje y la velocidad se convierten en nuestras primeras relaciones muy básicas que pueden ser utilizadas para determinar el rendimiento de una aeronave.
4.2 Puesto aerodinámico
Anteriormente discutimos el puesto aerodinámico. Para un perfil aerodinámico (2‑D) o un ala (3‑D), a medida que se incrementa el ángulo de ataque se alcanza un punto donde disminuye el incremento en el coeficiente de sustentación, que acompaña al incremento del ángulo de ataque. Cuando esto ocurre, la curva de coeficiente de sustentación versus ángulo de ataque se vuelve no lineal a medida que el flujo sobre la superficie superior del ala comienza a separarse de la superficie. Esta separación del flujo puede ser gradual, generalmente progresando desde el borde posterior del ala o ala y avanzando; repentina, a medida que el flujo se separa de grandes porciones del ala al mismo tiempo; o alguna combinación de los dos. La naturaleza real de la pérdida dependerá de la forma de la sección aerodinámica, la forma en planta del ala y el número de Reynolds del flujo.
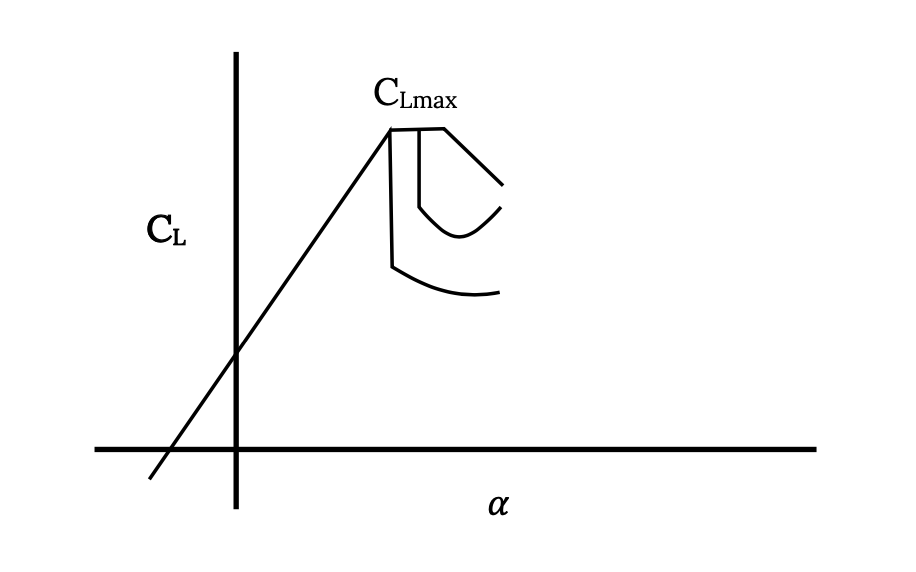
Definimos el ángulo de ataque de calado como el ángulo donde el coeficiente de sustentación alcanza un máximo, CLmax, y usamos este valor de coeficiente de sustentación para calcular una velocidad de calado para vuelo recto y nivelado.
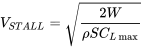
Tenga en cuenta que la velocidad de calado dependerá de una serie de factores, incluida la altitud. Si nos fijamos en una velocidad de parada equivalente al nivel del mar tenemos
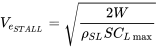
Se debe enfatizar que la velocidad de calado como se definió anteriormente se basa en la elevación igual al peso o vuelo recto y nivelado. Esta es la velocidad de calado citada en todos los manuales de operación de las aeronaves y utilizada como referencia por los pilotos. Hay que recordar que la parada es sólo una función del ángulo de ataque y puede ocurrir a cualquier velocidad. La definición de velocidad de calado utilizada anteriormente resulta de limitar el vuelo a condiciones rectas y niveladas donde la elevación equivale al peso. Esta velocidad de calado no es aplicable para otras condiciones de vuelo. Por ejemplo, en un giro la elevación normalmente excederá el peso y la parada ocurrirá a una velocidad de vuelo más alta. Lo mismo ocurre en condiciones de vuelo acelerado como el ascenso. Por esta razón se enseña a los pilotos a manejar el puesto en vuelo de escalada y giro así como en vuelo recto y nivelado.
Para la mayor parte de este texto trataremos el vuelo que se asume recto y nivelado y por lo tanto asumiremos que la velocidad de calada recta y nivelada mostrada arriba es relevante. Esta velocidad generalmente representa la velocidad de vuelo recta y nivelada práctica más baja para una aeronave y, por lo tanto, es un parámetro importante de rendimiento de la aeronave.
Normalmente definiremos la velocidad de calado para una aeronave en términos del peso bruto máximo de despegue pero hay que señalar que el peso de cualquier aeronave cambiará en vuelo a medida que se utilice combustible. Para una altitud dada, a medida que cambia el peso, la variación de velocidad de calado con el peso se puede encontrar de la siguiente
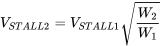
Es obvio que a medida que avanza un vuelo y disminuye el peso de la aeronave, la velocidad de calado también disminuye. Dado que la velocidad de calado representa un límite inferior de velocidad de vuelo recta y nivelada, es una indicación de que una aeronave generalmente puede aterrizar a una velocidad menor que la velocidad mínima de despegue.
Para muchos aviones de transporte grandes, la velocidad de calado del avión completamente cargado es demasiado alta para permitir un aterrizaje seguro dentro de la misma distancia que se necesita para el despegue. En los casos en que una aeronave deba regresar a su campo de despegue para aterrizar debido a alguna situación de emergencia (como la falla del tren de aterrizaje para retraerse), deberá volcar o quemar combustible antes de aterrizar para reducir su peso, velocidad de calado y velocidad de aterrizaje. El despegue y el aterrizaje se discutirán en un capítulo posterior con mucho más detalle.
4.3 Perspectivas sobre el Stall
Al discutir el puesto vale la pena considerar algunos de los aspectos físicos del puesto y los muchos conceptos erróneos que tanto los pilotos como el público tienen con respecto al puesto.
Para el ingeniero aeroespacial, el puesto es C Lmax, la mayor capacidad de elevación posible de la aeronave; pero, para la mayoría de los pilotos y el público, ¡el puesto es donde el avión pierde toda la elevación! ¿Cómo pueden ser las dos? Y, si uno de estos puntos de vista está equivocado, ¿por qué?
La clave para comprender ambas perspectivas de la parada es comprender la diferencia entre el coeficiente de elevación y elevación. La elevación es el producto del coeficiente de sustentación, la presión dinámica y el área de forma plana del ala. Para una altitud dada y la elevación del avión (área del ala) entonces depende del coeficiente de elevación y la velocidad. Es posible tener un coeficiente de sustentación muy alto C L y una elevación muy baja si la velocidad es baja.
Cuando un avión está en un ángulo de ataque tal que se alcanza C Lmax, el ángulo de ataque alto también da como resultado un alto coeficiente de arrastre. La alta resistencia resultante normalmente conduce a una reducción en la velocidad del aire que luego resulta en una pérdida de sustentación. En un avión de diseño convencional esto será seguido por una caída de la nariz de la aeronave hacia una actitud de nariz abajo y una pérdida de altitud a medida que se recupera la velocidad y se recupera la elevación. Si el piloto intenta levantar la nariz del avión, el avión simplemente caerá en actitud de nariz arriba. A los pilotos se les enseña a dejar caer la nariz tan pronto como perciban la parada para que la elevación y la recuperación de altitud puedan comenzar lo más rápido posible. Un buen instructor de vuelo le enseñará a un piloto a detectar la parada al inicio de tal manera que la recuperación pueda comenzar antes de que se pierda la altitud y el levantamiento.
Cabe señalar que si una aeronave tiene suficiente potencia o empuje y el alto arrastre presente en C Lmax se puede igualar por empuje, el vuelo puede continuar en la región de la calada y posterior al calado. Esto es posible en muchos aviones de combate y el reino de vuelo posterior a la parada ofrece muchas posibilidades interesantes de maniobra en una “pelea de perros”.
El público en general tiende a pensar en el puesto como cuando el avión cae del cielo. Esto se puede ver en casi cualquier reporte periodístico de un accidente de avión donde la historia dirá “el avión se estancó y cayó del cielo, cayendo en picado en el suelo después de que falló el motor”. Este tipo de reporte tiene varios errores. La parada no tiene nada que ver con los motores y una pérdida del motor no causa parada. Los veleros pueden pararse sin tener motor y a cada piloto se le enseña a volar un avión a un aterrizaje seguro cuando se pierde un motor. El puesto tampoco provoca que un avión entre en una inmersión. Sin embargo, es posible que un piloto entre en pánico ante la pérdida de un motor, inadvertidamente entre en un puesto, no tome las acciones adecuadas de recuperación de la parada y tal vez “caiga en picado” en el suelo.
4.4 Arrastre y empuje requeridos
Como se ha visto anteriormente, para vuelo recto y nivelado, el empuje debe ser igual al arrastre. El arrastre es una función del coeficiente de arrastre C D que es, a su vez, una función de un arrastre base y un arrastre inducido.
C D = C D0 + C Di
Suponemos que esta relación tiene una forma parabólica y que el coeficiente de arrastre inducido tiene la forma
C Di = KC L 2
Por lo tanto, escribimos
C D = C D0 + KC L 2
A partir de la teoría aerodinámica inviscida, se encuentra que K es una función de la relación de aspecto y la forma plana del ala

donde e es la unidad para una forma elíptica ideal de la distribución de sustentación a lo largo del tramo del ala y menos de una para distribuciones de sustentación no ideales en el sentido de la envergadura.
La relación del coeficiente de arrastre mostrada anteriormente se denomina arrastre parabólico “polar” debido a su forma matemática. En realidad solo es válido para la teoría del ala inviscida, no para todo el avión. En este texto utilizaremos esta ecuación como una primera aproximación al comportamiento de arrastre de un avión entero. Si bien esto es solo una aproximación, es bastante bueno para un curso de rendimiento de nivel introductorio. Sin embargo, puede resultar en algunas estimaciones de rendimiento poco realistas cuando se usa con algunos datos reales de aeronaves.
El arrastre de la aeronave se encuentra a partir del coeficiente de arrastre, la presión dinámica y el área de planform del ala:
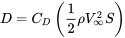
Por lo tanto,
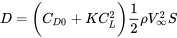
Al darse cuenta de que para el vuelo recto y nivelado, la elevación es igual al peso y la elevación es una función del coeficiente de elevación del ala, podemos escribir:
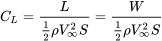
dando:
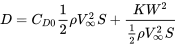
La ecuación anterior solo es válida para vuelo recto y nivelado para una aeronave en flujo incompresible con un arrastre polar parabólico.
Veamos la forma de esta ecuación y examinemos su significado físico. Para un avión dado a una altitud dada la mayoría de los términos en la ecuación son constantes y podemos escribir
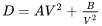
donde
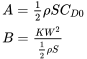
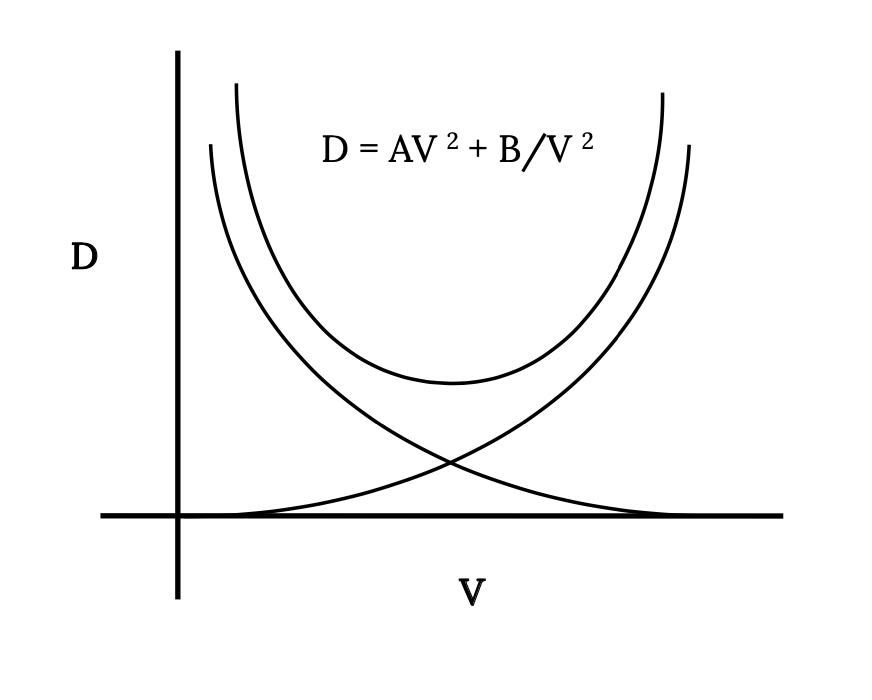
El primer término de la ecuación muestra que parte del arrastre aumenta con el cuadrado de la velocidad. Este es el término de arrastre base y es lógico que para la forma básica del avión el arrastre aumente a medida que aumente la presión dinámica. Para la mayoría de los observadores esto es algo intuitivo.
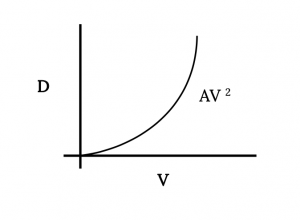
El segundo término representa una resistencia que disminuye a medida que aumenta el cuadrado de la velocidad. Da un arrastre infinito a velocidad cero, sin embargo, este es un límite inalcanzable para aviones normalmente definidos, de ala fija (a diferencia de elevación vertical). Cabe señalar que este término incluye la influencia de la elevación o coeficiente de sustentación sobre la resistencia al arrastre. Cuanto más rápido vuela una aeronave, menor es el valor del coeficiente de sustentación necesario para dar una elevación igual al peso. El coeficiente de elevación, se recuerda, es una función lineal del ángulo de ataque (hasta el calado). Si una aeronave está volando recto y nivelado y el piloto mantiene vuelo nivelado mientras disminuye la velocidad del avión, el ángulo de ataque del ala debe aumentar para proporcionar el coeficiente de sustentación y elevación necesarios para igualar el peso. A medida que aumenta el ángulo de ataque es algo intuitivo que aumente el arrastre del ala. A medida que disminuye la velocidad en vuelo recto y nivelado, esta parte del arrastre continuará aumentando exponencialmente hasta que se alcance la velocidad de calado.
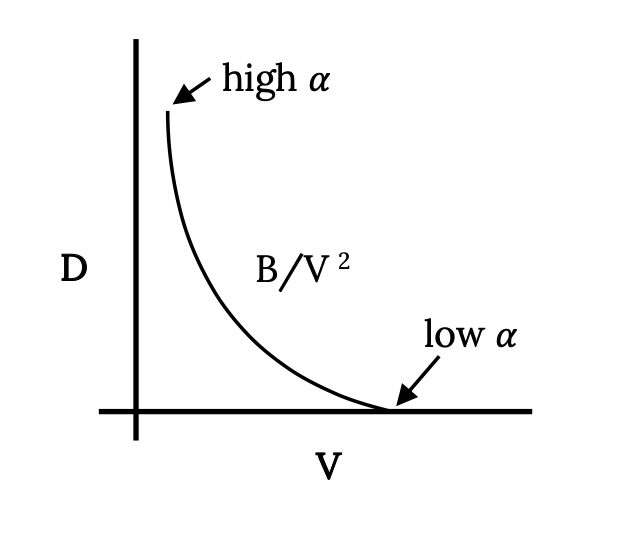
Al sumar los dos términos de arrastre se obtiene la siguiente figura que muestra la variación de arrastre completa con la velocidad para una aeronave con un polar de arrastre parabólico en vuelo recto y nivelado.
4.5 Arrastre mínimo
Un punto de interés obvio en la gráfica de arrastre anterior es la velocidad para el arrastre mínimo. Esto se puede encontrar, por supuesto, gráficamente a partir de la trama. También podemos echar un vistazo simple a las ecuaciones para encontrar alguna otra información sobre las condiciones para el arrastre mínimo.
Los requisitos para el arrastre mínimo son intuitivamente de interés porque parece que deberían relacionarse de alguna manera con la economía de vuelo. Posteriormente encontraremos que hay ciertos óptimos de rendimiento que dependen directamente del vuelo en condiciones mínimas de arrastre.
En este punto estamos hablando de encontrar la velocidad a la que el avión está volando en condiciones mínimas de arrastre en vuelo recto y nivelado. Es importante tener presente esta suposición. Posteriormente encontraremos que ciertos optima de ascenso y deslizamiento ocurren en estas mismas condiciones y estiraremos nuestra suposición recta y nivelada a una de vuelo “cuasi” ‑nivel.
Podemos comenzar con una mirada muy simple a lo que nuestros equilibrios de elevación, arrastre, empuje y peso para vuelo recto y nivelado nos dicen sobre las condiciones mínimas de arrastre y luego pasaremos a una mirada más sofisticada sobre cómo los términos dependientes de la forma del ala en la ecuación polar de arrastre (CD0 y K) están relacionados al mínimo condición de arrastre. En última instancia, lo más importante a determinar es la velocidad de vuelo con mínima resistencia porque el piloto puede entonces usar esta para volar en condiciones mínimas de arrastre.
Veamos nuestras simples relaciones de fuerza estática:
L = W, T = D
escribir
D = Ancho x D/L
que dice que el arrastre mínimo ocurre cuando el arrastre dividido por sustentación es mínimo o, inversamente, cuando el levantamiento dividido por arrastre es un máximo.
Esta combinación de parámetros, L/D, ocurre a menudo al observar el rendimiento de la aeronave. En general, suele ser intuitivo que cuanto mayor sea el levantamiento y menor sea el arrastre, mejor será un avión. No es tan intuitivo que la relación máxima de elevación-resistencia se produzca en las mismas condiciones de vuelo que el arrastre mínimo. Este simple análisis, sin embargo, muestra que
El arrastre mínimo se produce cuando L/D es MÁXIMO.
Tenga en cuenta que como C L/C D = L/D también podemos decir que el arrastre mínimo ocurre cuando C L /C D es máximo. Es muy importante tener en cuenta que el arrastre mínimo no connota el coeficiente mínimo de arrastre.
El arrastre mínimo ocurre en un solo valor de ángulo de ataque donde el coeficiente de sustentación dividido por el coeficiente de arrastre es un máximo:
D min ocurre cuando (C L/C D) max
Como se señaló anteriormente, esto no es en el mismo ángulo de ataque en el que C D está en un mínimo. Tampoco es el mismo ángulo de ataque donde el coeficiente de sustentación es máximo. Esto debería ser bastante obvio ya que C Lmax ocurre en la parada y la resistencia es muy alta en la parada.
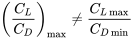
Dado que el arrastre mínimo es una función solo de la relación de los coeficientes de sustentación y arrastre y no de altitud (densidad), el valor real de la resistencia mínima para una aeronave dada a un peso dado será invariable con la altitud. La velocidad real a la que ocurre el arrastre mínimo es una función de la altitud y generalmente aumentará a medida que aumente la altitud.
Si asumimos un polar de arrastre parabólico y trazamos la ecuación de arrastre
para arrastre versus velocidad a diferentes altitudes, las curvas resultantes se parecerán a lo siguiente:
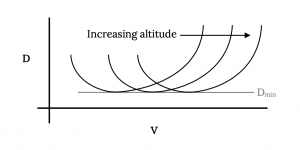
Tenga en cuenta que el arrastre mínimo será el mismo en cada altitud como se mencionó anteriormente y la velocidad para arrastre mínimo aumentará con la altitud.
Discutimos en una sección anterior el hecho de que debido a la relación entre la presión dinámica a nivel del mar con la de altitud, la aeronave siempre realizaría lo mismo a la misma velocidad aérea indicada o equivalente a nivel del mar. De hecho, si se escribe la ecuación de arrastre como una función de la densidad del nivel del mar y la velocidad equivalente al nivel del mar, se obtendrá una sola curva.
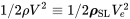
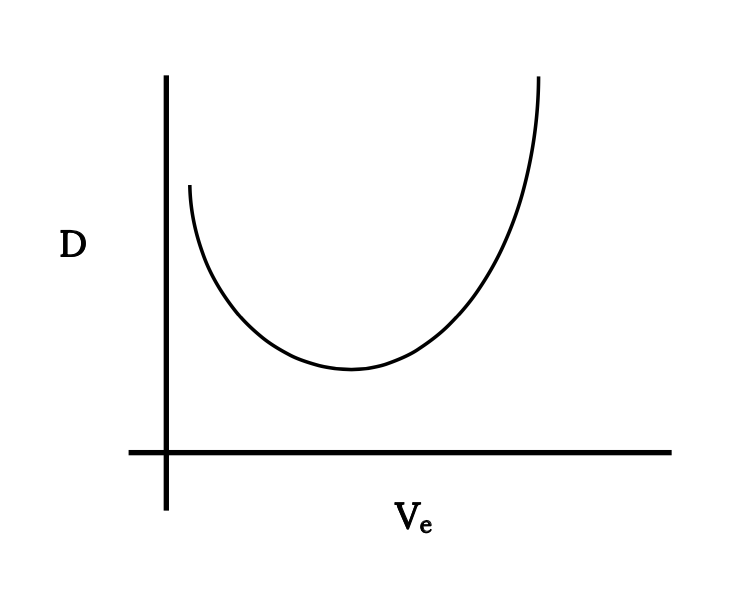
Para encontrar el comportamiento de arrastre versus velocidad de una aeronave, entonces solo es necesario hacer cálculos o parcelas a nivel del mar y luego convertir a las verdaderas velocidades aéreas para volar a cualquier altitud usando la relación de velocidad a continuación.
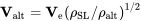
4.6 Resumen mínimo de arrastre
Sabemos que la resistencia mínima ocurre cuando la relación de sustentación a arrastre está en un máximo, pero cuando ocurre eso; ¿a qué valor de C L o C D o a qué velocidad?
Una forma de encontrar C L y C D con arrastre mínimo es trazar uno contra el otro como se muestra a continuación. El valor máximo de la relación entre el coeficiente de sustentación y el coeficiente de arrastre será donde una línea del origen solo tangente a la curva toque la curva. En este punto están los valores de C L y C D para arrastre mínimo. Este método gráfico de encontrar los parámetros mínimos de arrastre funciona para cualquier aeronave aunque no tenga un arrastre polar parabólico.
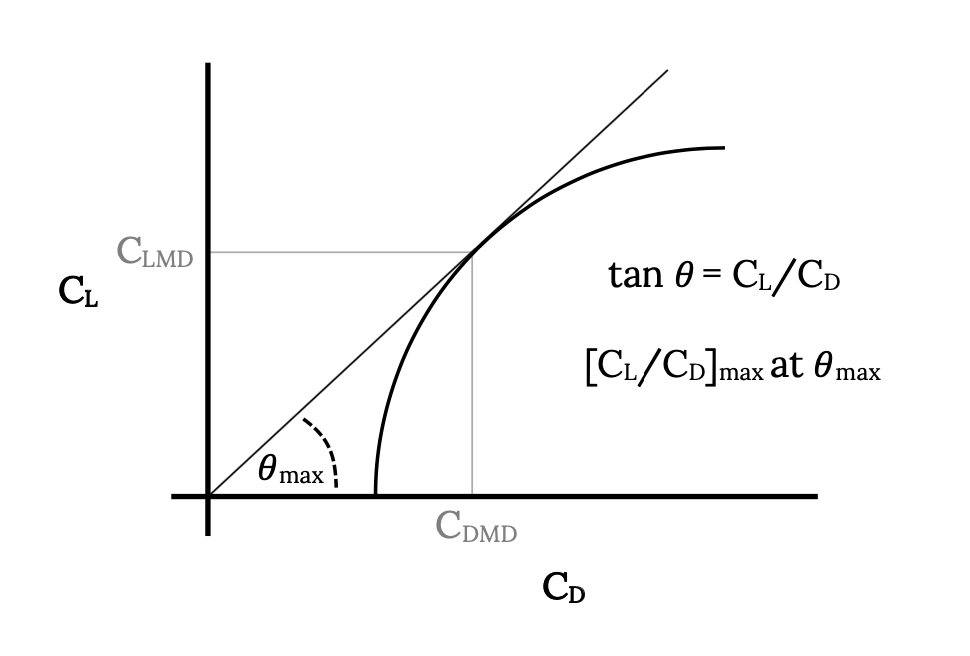
Una vez que se encuentran C Lmd y C Dmd, la velocidad para el arrastre mínimo se encuentra a partir de la siguiente ecuación, siempre que la aeronave esté en vuelo recto y nivelado
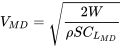
Como ya sabemos, la velocidad para arrastre mínimo se puede encontrar para las condiciones del nivel del mar (la velocidad equivalente al nivel del mar) y a partir de eso es fácil encontrar la velocidad mínima de arrastre a altitud.
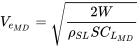
También hay que señalar que cuando se conocen los coeficientes de sustentación y arrastre para la resistencia mínima y se conoce el peso de la aeronave, la resistencia mínima en sí se puede encontrar a partir de
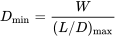
Es común suponer que la relación entre arrastre y elevación es la que encontramos anteriormente, la llamada drag polar parabólica. Para el arrastre parabólico polar
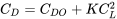
es fácil tomar la derivada con respecto al coeficiente de sustentación y establecerla igual a cero para determinar las condiciones para la relación mínima del coeficiente de arrastre al coeficiente de sustentación, que era una condición para el arrastre mínimo.
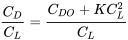
Por lo tanto,
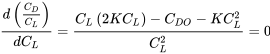
Esto da
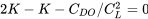
o
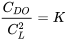
y
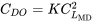
Lo anterior es la condición requerida para un arrastre mínimo con un arrastre parabólico polar.
Ahora, volvemos a la drag polar
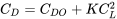
y para arrastre mínimo podemos escribir
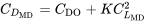
que, con lo anterior, da
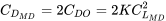
o
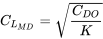
De esto podemos encontrar el valor de la relación máxima de elevación a arrastre en términos de parámetros básicos de arrastre
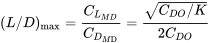
Y la velocidad a la que esto ocurre en vuelo recto y nivelado es
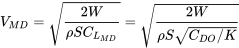
Así podemos escribir la velocidad mínima de arrastre como
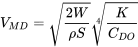
o la velocidad mínima de arrastre equivalente al nivel del mar como
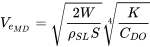
4.7 Revisión: Condiciones mínimas de arrastre para un Polar de arrastre parabólico
En este punto sabemos mucho sobre las condiciones mínimas de arrastre para una aeronave con una resistencia parabólica polar en vuelo recto y nivelado. Las siguientes ecuaciones pueden ser útiles en la solución de muchos problemas de desempeño diferentes para ser considerados más adelante en este texto. Habrá varias condiciones de vuelo que se verán optimizadas cuando se vuele en condiciones mínimas de arrastre. Por lo tanto, se sugiere que el alumno escriba las siguientes ecuaciones en una página separada en sus notas de clase para facilitar su referencia.
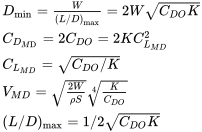
EJEMPLO 4.1
Una aeronave que pesa 3000 libras tiene un área de ala de 175 pies cuadrados y una relación de aspecto de siete con un factor de eficiencia aerodinámica del ala (e) de 0.95. Si el coeficiente de arrastre base, C DO, es 0.028, busque la resistencia mínima al nivel del mar y a una altitud de 10,000 pies, la relación máxima de sustentación a arrastre y los valores de coeficiente de sustentación y arrastre para el arrastre mínimo. También encuentra las velocidades para arrastre mínimo en vuelo recto y nivelado tanto a nivel del mar como a 10,000 pies. Primero tenemos que encontrar el término K en la ecuación de arrastre.
K = 1/(π ARe) = 0.048
Ahora podemos encontrar
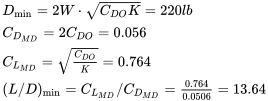
Podemos verificar esto con
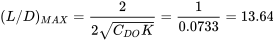
La velocidad para arrastre mínimo es la primera de estas que depende de la altitud.
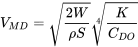
A nivel del mar
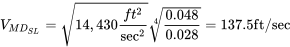
Para encontrar la velocidad de arrastre mínimo a 10,000 pies hacemos un recálculo usando la densidad a esa altitud o podemos usar
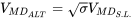
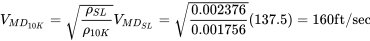
Se sugiere que en este punto el alumno utilice la ecuación de arrastre
y hacer gráficas de arrastre versus velocidad tanto para el nivel del mar como para las condiciones de altitud de 10,000 pies, trazando valores de arrastre a incrementos de 20 fps. Las gráficas confirmarían los valores anteriores de velocidad mínima de arrastre y arrastre mínimo.
4.8 Volando con Arrastre Mínimo
Una pregunta que debería hacerse en este momento pero que generalmente no se responde en un texto sobre el rendimiento de la aeronave es “¿Cómo diablos hace que el piloto haga que ese avión vuele en condiciones mínimas de arrastre de todos modos?”
La respuesta, sencillamente, es volar a la velocidad equivalente del nivel del mar para condiciones mínimas de arrastre. El piloto instala o “recorta” la aeronave para volar a altitud constante (recta y nivelada) a la velocidad aérea indicada (velocidad equivalente al nivel del mar) para un arrastre mínimo como se indica en el manual de operaciones de la aeronave. Todo lo que el piloto necesita hacer es mantener la velocidad y la altitud constantes.
4.9 Arrastre en flujo compresible
Para efectos de un curso introductorio en el desempeño de aeronaves nos hemos limitado a la discusión de aviones de menor velocidad; es decir, aviones que operan en flujo incompresible. Como se discutió anteriormente, analíticamente, esto nos restringiría a la consideración de velocidades de vuelo de Mach 0.3 o menos (menos de 300 fps a nivel del mar), sin embargo, las realidades físicas del inicio de la subida de arrastre debido a los efectos de compresibilidad nos permiten extender nuestro uso de la teoría incompresible a números de Mach de alrededor 0.6 a 0.7. Este es el rango del número de Mach donde el flujo supersónico sobre lugares como la superficie superior del ala ha alcanzado la magnitud en que las ondas de choque pueden ocurrir durante la desaceleración del flujo, lo que resulta en pérdidas de energía a través del choque y en aumentos de resistencia debido a la separación del flujo inducida por choque sobre la superficie del ala. Esta subida de arrastre se discutió en el Capítulo 3.
A medida que las velocidades ascienden a la región donde se deben considerar los efectos de compresiblilidad debemos tomar en cuenta la velocidad del sonido a y la relación de calores específicos de aire, gamma.
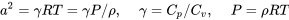
La gamma para el aire a temperaturas atmosféricas inferiores normales tiene un valor de 1.4.
Comenzando de nuevo con la relación para un arrastre polar parabólico, podemos multiplicar y dividir por la velocidad del sonido para reescribir la relación en términos de número Mach.
donde
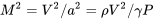
o
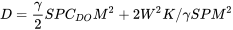
La ecuación resultante anterior es muy similar en forma a la relación polar de arrastre original y puede ser utilizada de manera similar. Por ejemplo, para encontrar el número de Mach para arrastre mínimo en vuelo recto y nivelado tomaríamos la derivada con respecto al número de Mach y estableceríamos el resultado igual a cero. La complicación es que algunos términos que consideramos constantes bajo condiciones incompresibles como K y CDO ahora pueden ser funciones del número de Mach y deben ser evaluados así.
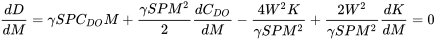
A menudo la ecuación anterior debe resolverse itterativamente.
4.10 Revisión
Hasta este punto hemos examinado la resistencia de una aeronave basada principalmente en un modelo simple utilizando una representación parabólica de arrastre en flujo incompresible. Hemos restringido aún más nuestro análisis al vuelo recto y nivelado donde la elevación es igual al peso y el empuje es igual a arrastre.
El avión puede volar recto y nivelado a una amplia gama de velocidades, siempre que haya suficiente potencia o empuje para igualar o superar la resistencia a esas velocidades. El alumno necesita comprender los aspectos físicos de este vuelo.
Observamos la velocidad para vuelo recto y nivelado en condiciones mínimas de arrastre. Uno podría, por supuesto, navegar siempre a esa velocidad y podría, de hecho, ser una forma muy económica de volar (lo examinaremos más adelante en una discusión de alcance y resistencia). No obstante, dado que “el tiempo es dinero” puede haber razones para viajar a velocidades más altas. También podría ser más divertido volar más rápido. El vuelo a velocidades de arrastre superiores a las mínimas requerirá menos ángulo de ataque para producir la elevación necesaria (para igualar el peso) y el límite de velocidad superior estará determinado por el empuje máximo o potencia disponible del motor.
Es posible que se desee un crucero a velocidades de arrastre inferiores a las mínimas cuando el vuelo se acerca al aterrizaje o al volar en patrones de retención o cuando vuele en otras misiones de propósito especial. Esto requerirá un ángulo de ataque superior al mínimo de arrastre y el uso de más empuje o potencia para superar el aumento resultante en la resistencia. El límite inferior de velocidad podría entonces ser el resultado de que la resistencia aerodinámica alcance la magnitud de la potencia o el empuje disponible del motor; sin embargo, normalmente resultará del ángulo de ataque que alcanza el ángulo de calado. Por lo tanto, la velocidad de calado normalmente representa el límite inferior en velocidad de crucero recta y nivelada.
Hay que recordar que todo lo anterior se basa en una suposición de vuelo recto y nivelado. Si una aeronave está volando en línea recta y se agrega nivel a una velocidad y potencia o empuje dadas, el avión inicialmente acelerará y ascenderá hasta que se alcance una nueva recta y equilibrio de nivel a una altitud mayor. El piloto puede controlar esta adición de energía cambiando la actitud del avión (ángulo de ataque) para dirigir la energía agregada hacia la combinación deseada de aumento de velocidad y/o aumento de altitud. Si disminuye la potencia del motor, normalmente se esperaría una disminución en la altitud y/o velocidad, dependiendo de la entrada del control del piloto.
Ahora debemos agregar el factor de salida del motor, ya sea empuje o potencia, a nuestra consideración del rendimiento. Es normal referirse a la salida de un motor a reacción como empuje y de un motor de hélice como potencia. Primero consideraremos el más simple de los dos casos, el empuje.
4.11 Empuje
Nosotros hemos dicho que para una aeronave en vuelo recto y nivelado, el empuje debe ser igual a arrastre. Si el empuje del motor de la aeronave excede el arrastre para un vuelo recto y nivelado a una velocidad determinada, el avión subirá o acelerará o hará ambas cosas. También podría utilizarse para hacer giros u otras maniobras. Por lo tanto, el arrastre encontrado en vuelo recto y nivelado podría llamarse el empuje requerido (para vuelo recto y nivelado). El empuje realmente producido por el motor se denominará el empuje disponible.
Si bien podemos hablar de la salida de cualquier motor de avión en términos de empuje, es convencional referirse al empuje de los motores a reacción y a la potencia de los motores de hélice. Una hélice, por supuesto, produce empuje tal como lo hace el flujo de un motor a reacción; sin embargo, para un motor que alimenta una hélice (ya sea pistón o turbina), la salida del motor en sí es potencia a un eje. Así, cuando se habla de tal sistema de propulsión la mayoría de las referencias son a su potencia. Cuando se habla de la propia hélice, se puede utilizar la terminología de empuje.
Las unidades empleadas para las discusiones de empuje son Newtons en el sistema SI y libras en el sistema inglés. Dado que las unidades inglesas de libras todavía se usan casi universalmente cuando se habla de empuje, normalmente se usarán aquí.
El empuje es una función de muchas variables, incluidas las eficiencias en varias partes del motor, el ajuste del acelerador, la altitud, el número de Mach y la velocidad. Un estudio completo del empuje del motor se dejará para un curso de propulsión posterior. Para nuestros propósitos bastarán modelos muy simples de empuje con suposiciones de que el empuje varía con la densidad (altitud) y el ajuste del acelerador y posiblemente, la velocidad. Ya encontramos una de esas relaciones en el capítulo dos con la ecuación de momentum. A menudo simplificaremos las cosas aún más y asumiremos que el empuje es invariante con la velocidad para un simple motor a reacción.
Si conocemos la variación de empuje con velocidad y altitud para una aeronave determinada, podemos agregar las curvas de empuje del motor a las curvas de arrastre para vuelo recto y nivelado para esa aeronave como se muestra a continuación. Normalmente asumiremos que dado que estamos interesados en los límites de rendimiento para la aeronave solo nos interesa el caso del ajuste del acelerador al 100%. Es obvio que otros ajustes del acelerador darán empujes en cualquier punto por debajo de las curvas del 100% para el empuje.
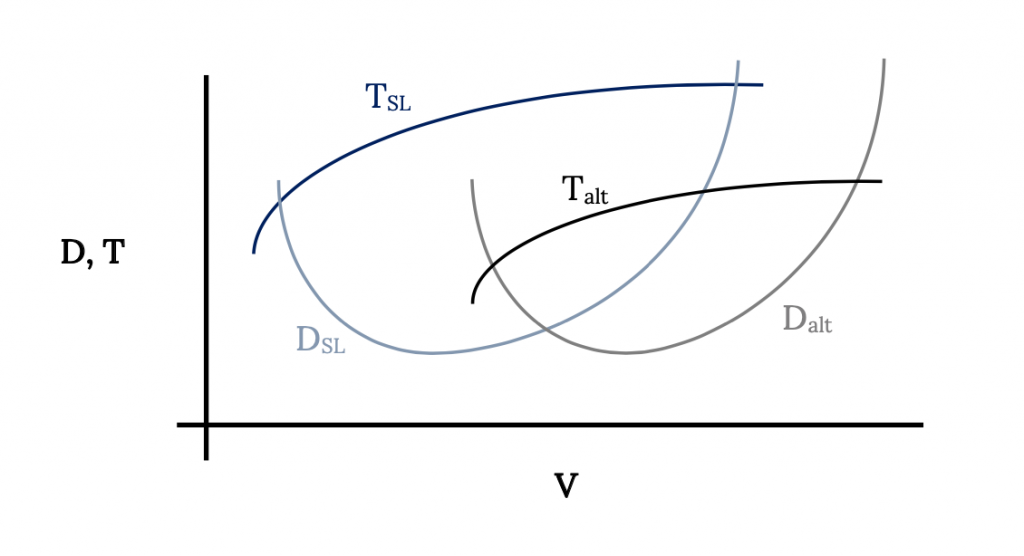
En la figura anterior cabe señalar que, aunque la terminología utilizada es empuje y arrastre, puede ser más significativo llamar a estas curvas empuje disponible y empuje requerido al referirse a la salida del motor y al arrastre de la aeronave, respectivamente.
4.12 Velocidades mínimas y máximas
Las intersecciones de las curvas de empuje y arrastre en la figura anterior representan obviamente las velocidades de vuelo mínima y máxima en vuelo recto y nivelado. Por encima de la velocidad máxima no hay suficiente empuje disponible del motor para superar el arrastre (empuje requerido) de la aeronave a esas velocidades. Lo mismo ocurre por debajo de la intersección de menor velocidad de las dos curvas.
La verdadera limitación de velocidad más baja para la aeronave generalmente se impone por la pérdida en lugar de la intersección de las curvas de empuje y arrastre. La velocidad de calado se puede agregar a la gráfica como se muestra a continuación:
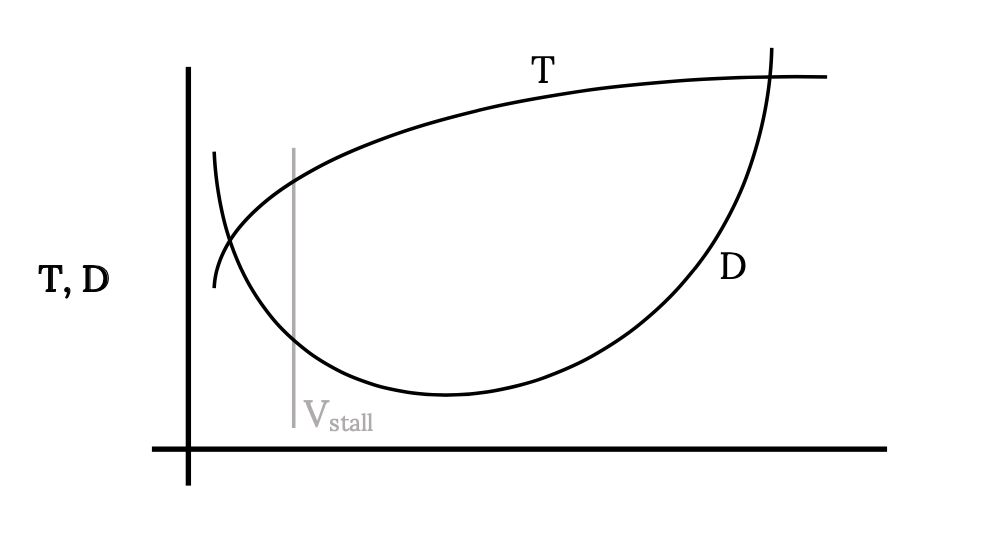
El área entre el empuje disponible y las curvas de arrastre o empuje requeridas se puede llamar envolvente de vuelo. El avión puede volar recto y nivelado a cualquier velocidad entre estos puntos de intersección de velocidad superior e inferior. Entre estos límites de velocidad hay un exceso de empuje disponible que se puede utilizar para vuelos que no sean rectos y nivelados. Este exceso de empuje se puede utilizar para escalar o girar o maniobrar de otras maneras. Analizaremos algunas de estas maniobras en un capítulo posterior. Por ahora limitaremos nuestra investigación al ámbito del vuelo recto y nivelado.
Tenga en cuenta que a mayor altitud, la disminución del empuje disponible ha reducido la “envolvente de vuelo”, acercando los límites de velocidad superior e inferior y reduciendo el exceso de empuje entre las curvas. A medida que el empuje se reduce continuamente con el aumento de la altitud, la envolvente del vuelo continuará encogiéndose hasta que las velocidades superior e inferior se vuelvan iguales y las dos curvas simplemente se toquen. Esto se puede ver más claramente en la siguiente figura donde se trazan todos los datos en términos de velocidad equivalente a nivel del mar. En el ejemplo mostrado, el empuje disponible en h 6 cae completamente por debajo de la curva de arrastre o empuje requerida. Esto significa que el avión no puede volar recto y nivelado a esa altitud. Se dice que esa altitud está por encima del “techo” para la aeronave. A cierta altitud entre h 5 y h 6 pies habrá una curva de empuje disponible que solo tocará la curva de arrastre. Esa altitud será la altura máxima del avión, la altitud a la que el avión sólo puede volar a una sola velocidad. Tendremos más que decir sobre las definiciones de techo en una sección posterior.
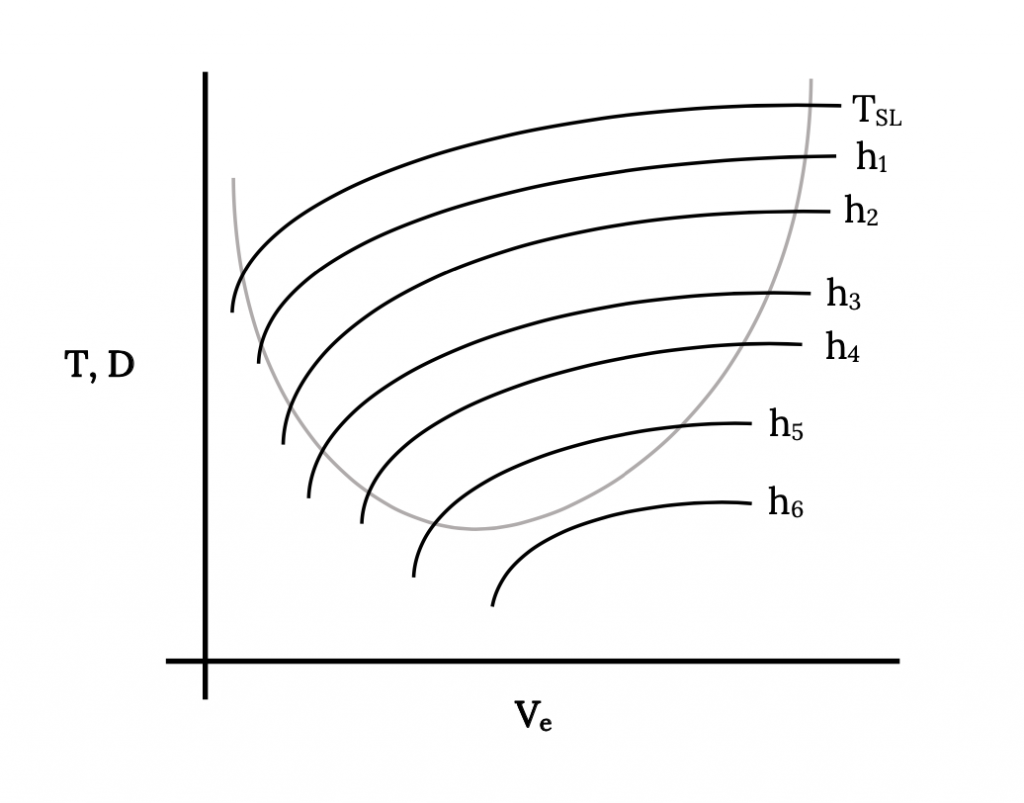
Otra forma de observar estos mismos límites de velocidad y altitud es trazar las intersecciones de las curvas de empuje y arrastre en la figura anterior contra la altitud como se muestra a continuación. Esto muestra otra versión de una envolvente de vuelo en términos de altitud y velocidad. Este tipo de parcela es más significativo para el piloto y para el ingeniero de pruebas de vuelo ya que la velocidad y la altitud son dos parámetros que se muestran en los instrumentos estándar de la aeronave y el empuje no lo es.
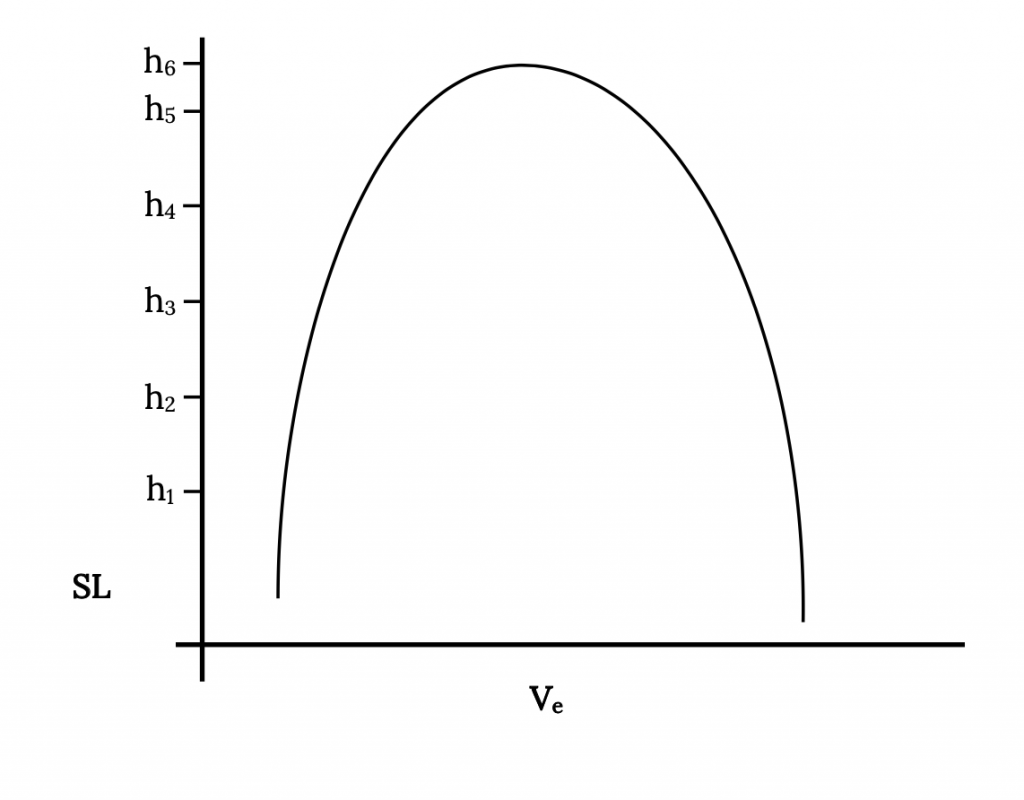
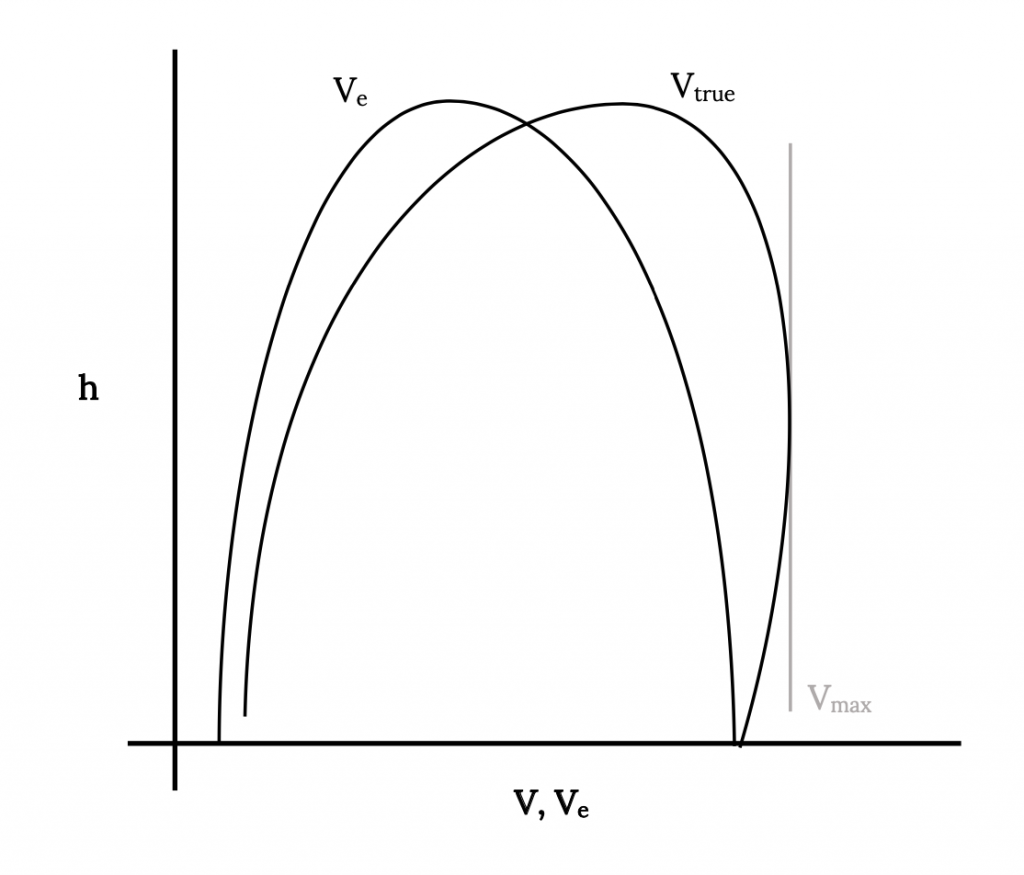
También puede ser significativo agregar a la figura anterior una gráfica de los mismos datos usando la velocidad aérea real en lugar de las velocidades aéreas indicadas o equivalentes a nivel del mar. Esto se puede hacer de manera bastante simple usando la raíz cuadrada de la relación de densidad (nivel del mar a altitud) como se discutió anteriormente para convertir las velocidades equivalentes a velocidades reales. Esto se muestra en la gráfica a continuación. Tenga en cuenta que a nivel del mar V = Ve y también habrá cierta altitud donde haya una velocidad máxima verdadera del aire.
4.13 Caso Especial de Empuje Constante
A menudo se emplea un modelo muy simple para el empuje de un motor a reacción. Se hace la suposición de que el empuje es constante a una altitud dada. Utilizaremos esta suposición como nuestro modelo estándar para todos los aviones a reacción a menos que se indique lo contrario en ejemplos o problemas. Posteriormente discutiremos modelos para variación de empuje con altitud.
El modelo anterior (empuje constante a altitud) obviamente permite encontrar una solución analítica bastante simple para las intersecciones del empuje disponible y las curvas de arrastre (empuje requerido). Vamos a dejar que el empuje sea igual a una constante
T = T 0
por lo tanto, en vuelo recto y nivelado donde el empuje es igual a arrastre, podemos escribir
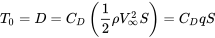
donde q es una abreviatura de uso común para la presión dinámica.
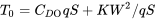
o
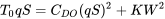
y reordenando como una ecuación cuadrática
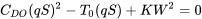
Resolver la ecuación anterior da
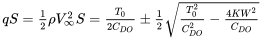
o
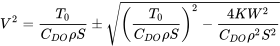
En cuanto a la velocidad equivalente al nivel del mar
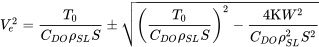
Estas soluciones son, por supuesto, doblemente valoradas. La mayor velocidad es la velocidad máxima de vuelo recta y nivelada a la altitud en consideración y la solución más baja es la velocidad mínima nominal de vuelo recta y nivelada (la velocidad de calado probablemente será una velocidad mayor, lo que representa la verdadera velocidad de vuelo mínima).
Existen, por supuesto, otras formas de resolver para la intersección de las curvas de empuje y arrastre. A veces es conveniente resolver las ecuaciones para los coeficientes de elevación a las velocidades mínima y máxima. Para establecer tal solución primero volvemos a las ecuaciones básicas de vuelo recto y de nivel T = T 0 = D y L = W.
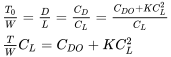
o
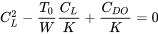
resolviendo para CL
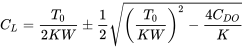
Esta solución dará dos valores del coeficiente de elevación. El mayor de los dos valores representa la velocidad mínima de vuelo para el vuelo recto y nivelado, mientras que el C L más pequeño es para la velocidad de vuelo máxima. La velocidad coincidente se encuentra a partir de la relación
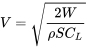
4.14 Reseña para Constant Thrust
La siguiente figura muestra gráficamente el caso discutido anteriormente. De la solución de la relación de empuje igual a arrastre obtenemos dos valores de coeficiente de sustentación o velocidad, uno para la velocidad máxima de vuelo recta y nivelada a la altitud elegida y el otro para la velocidad de vuelo mínima. La velocidad de calado probablemente superará la velocidad mínima de vuelo recta y nivelada encontrada a partir de la solución de empuje igual a arrastre, convirtiéndola en la verdadera velocidad de vuelo mínima.
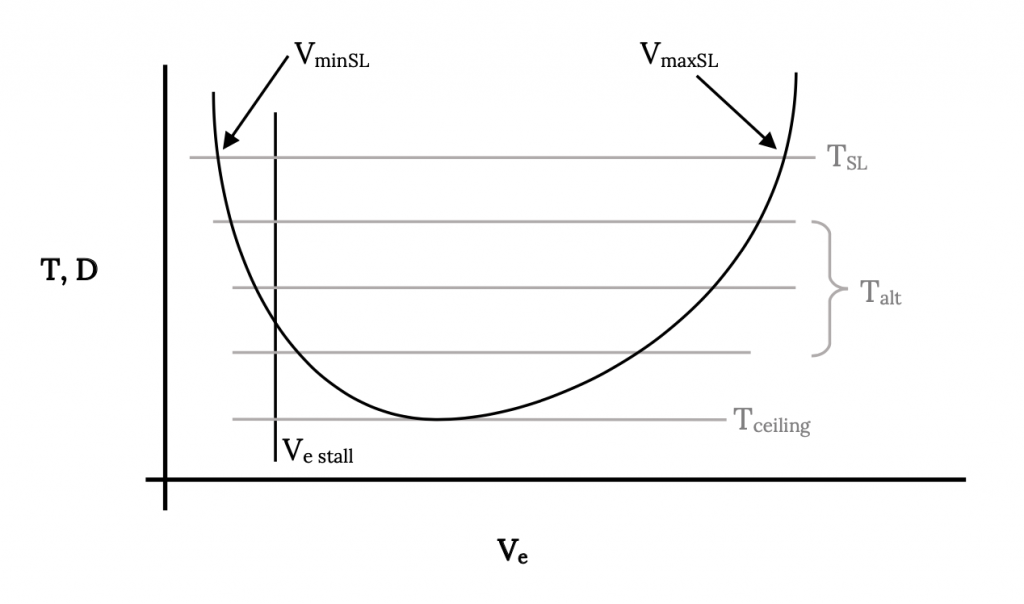
A medida que aumenta la altitud T 0 normalmente disminuirá y V MIN y V MAX se moverán juntos hasta que a una altitud de techo se fusionen para convertirse en un solo punto.
Normalmente se asume que el empuje de un motor a reacción variará con la altitud en proporción directa a la variación de densidad. Esta suposición está respaldada por las ecuaciones de empuje para un motor a reacción, ya que se derivan de las ecuaciones de impulso introducidas en el capítulo dos de este texto. Por lo tanto, podemos escribir:
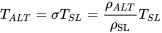
EJEMPLO 4.2
Anteriormente en este capítulo observamos un avión de 3000 libras con un área de ala de 175 pies cuadrados, relación de aspecto de siete y C DO de 0.028 con e = 0.95. Digamos que la aeronave está equipada con un pequeño motor a reacción que tiene un empuje constante al nivel del mar de 400 libras. Encuentre las velocidades de vuelo máximas y mínimas rectas y niveladas para esta aeronave a nivel del mar y a 10,000 pies asumiendo que el empuje disponible varía proporcionalmente a la densidad.
Si, como se sugirió anteriormente, el alumno, trazó las curvas de arrastre para esta aeronave, una solución gráfica es simple. Solo es necesario agregar una línea recta que represente 400 libras a la parcela del nivel del mar y las intersecciones de esta línea con la curva de arrastre del nivel del mar dan la respuesta. Lo mismo se puede hacer con los datos de altitud de 10,000 pies, utilizando un empuje constante reducido en proporción a la densidad.
Dada una densidad atmosférica estándar de 0.001756 sl/ft 3, el empuje a 10,000 pies será 0.739 veces el empuje del nivel del mar o 296 libras. Usando los dos valores de empuje disponibles podemos resolver los límites de velocidad a nivel del mar y a l0,000 pies.
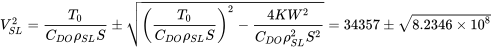
= 63053 o 5661
V SL = 251 pies/seg (máx.)
o = 75 pies/seg (min)
Por lo tanto, la ecuación da velocidades de vuelo máximas y mínimas rectas y niveladas como 251 y 75 pies por segundo respectivamente.
Se sugiere que el alumno haga cálculos similares para el caso de altitud de 10,000 pies. Tenga en cuenta que no se puede simplemente tomar las soluciones de velocidad del nivel del mar arriba y convertirlas en velocidades a altitud usando la raíz cuadrada de la relación de densidad. Las ecuaciones deben resolverse nuevamente utilizando el nuevo empuje a altitud. El estudiante también debe comparar los resultados de la solución analítica con los resultados gráficos.
Como se mencionó anteriormente, la velocidad de parada suele ser la velocidad mínima de vuelo real. Si el coeficiente máximo de sustentación tiene un valor de 1.2, busque las velocidades de calado a nivel del mar y agréguelas a sus gráficas.
4.15 Rendimiento en términos de potencia
La potencia del motor de todos los aviones propulsados por hélice se expresa en términos de potencia. El poder es realmente energía por unidad de tiempo. Si bien la propia salida de la hélice puede expresarse como empuje si se desea, es común expresarla también en términos de potencia.
Si bien a primera vista puede parecer que la potencia y el empuje son parámetros muy diferentes, están relacionados de una manera muy sencilla a través de la velocidad. El poder es el empuje multiplicado por la velocidad. Las unidades de potencia son Newton-metros por segundo o vatios en el sistema SI y caballos de fuerza en el sistema inglés. Como antes, utilizaremos principalmente el sistema inglés. El motivo es bastante obvio. ¡El autor desafía a cualquiera a encontrar cualquier piloto, mecánico o incluso cualquier conductor de automóvil en cualquier parte del mundo que pueda indicar la potencia nominal de su motor en vatios! Los vatios son para bombillas: ¡los caballos de fuerza son para motores!
En realidad, nuestras ecuaciones darán como resultado unidades de potencia del sistema inglés de pie‑libras por segundo. La conversión es
un HP = 550 pie-libras/segundo.
Hablaremos de dos tipos de energía; potencia disponible y potencia requerida. La potencia requerida es la potencia necesaria para superar el arrastre de la aeronave
P req = D x V
La potencia disponible es igual al empuje multiplicado por la velocidad.
P av = T x V
Cabe señalar que podemos comenzar con el poder y encontrar el empuje dividiendo por la velocidad, o podemos multiplicar el empuje por la velocidad para encontrar el poder. No hay razón para no hablar del empuje de un sistema de propulsión de hélice o de la potencia de un motor a reacción. El uso de la potencia para los sistemas de hélice y el empuje para los chorros simplemente sigue la convención y también reconoce que para un chorro, el empuje es relativamente constante con la velocidad y para una hélice, la potencia es relativamente invariante con la velocidad.
La potencia disponible es la potencia que se puede obtener de la hélice. Reconociendo que hay pérdidas entre el motor y la hélice distinguiremos entre la potencia disponible y los caballos de fuerza del eje. Los caballos de fuerza del eje son la potencia transmitida a través del cigüeñal o eje de transmisión a la hélice desde el motor. El motor puede ser de pistón o turbina o incluso eléctrico o de vapor. La hélice convierte esta potencia de eje (Ps) en potencia de propulsión con cierta eficiencia propulsiva, η p.
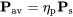
La eficiencia propulsiva es una función de la velocidad de la hélice, la velocidad de vuelo, el diseño de la hélice y otros factores.
Es obvio que tanto la potencia disponible como la potencia requerida son funciones de velocidad, tanto por el término de velocidad en la relación como por la variación tanto de arrastre como de empuje con velocidad. Para el motor a reacción ideal que suponemos que tiene un empuje constante, la variación en la potencia disponible es simplemente un aumento lineal con la velocidad.
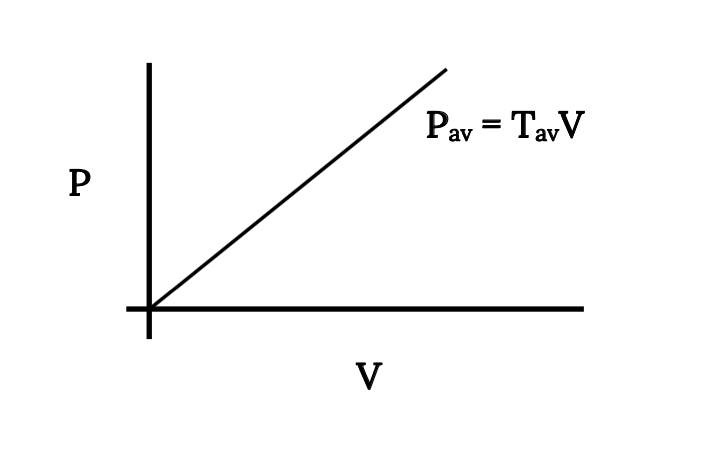
Es interesante que si estamos trabajando con un jet donde el empuje es constante con respecto a la velocidad, las ecuaciones anteriores dan potencia cero a velocidad cero. Esto no es intuitivo pero, sin embargo, es cierto y tendrá consecuencias interesantes cuando luego examinemos las tasas de ascenso.
Otra consecuencia de esta relación entre el empuje y la potencia es que si se asume que la potencia es constante con respecto a la velocidad (como haremos con los aviones de apoyo) el empuje se vuelve infinito a medida que la velocidad se acerca a cero. Esto significa que un Cessna 152 cuando está parado con el motor funcionando tiene infinitamente más empuje que un Boeing 747 con motores funcionando a toda velocidad. ¡También tiene más poder! ¡Qué impulso de ego para el piloto privado!
Al usar el concepto de poder para examinar el rendimiento de los aviones haremos lo mismo que hicimos con el empuje. Hablaremos de la intersección de las curvas de potencia requerida y potencia disponible determinando las velocidades máxima y mínima. Encontraremos la velocidad para la potencia mínima requerida. Veremos la variación de estos con la altitud. Las gráficas que trazamos se verán así a continuación.
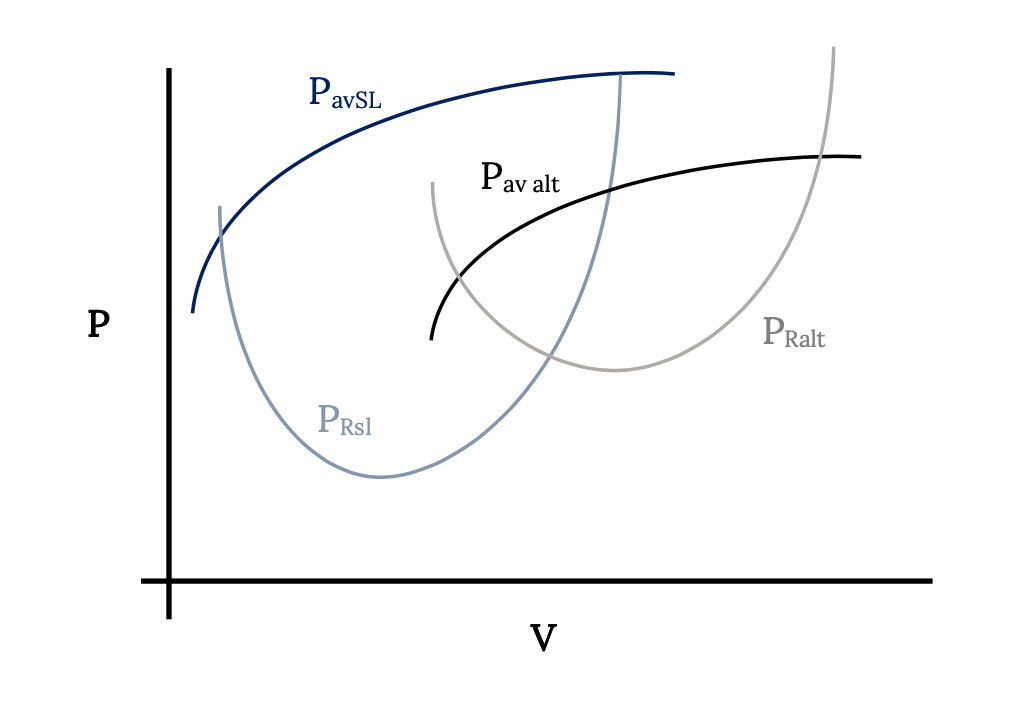
Si bien las velocidades de vuelo máximas y mínimas rectas y niveladas que determinemos a partir de las curvas de potencia serán idénticas a las encontradas a partir de los datos de empuje, habrá algunas diferencias. Una diferencia se puede notar a partir de la figura anterior. A diferencia del arrastre mínimo, que era de la misma magnitud en cada altitud, la potencia mínima será diferente en cada altitud. Esto significa que será más complicado colapsar los datos a todas las altitudes en una sola curva.
4.16 Energía requerida
La parcela de potencia requerida se verá muy similar a la vista anteriormente para el empuje requerido (arrastre). Es simplemente el arrastre multiplicado por la velocidad. Si seguimos asumiendo una resistencia parabólica polar con valores constantes de CDO y K tenemos la siguiente relación para la potencia requerida:
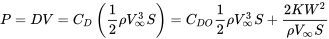
Podemos graficar esto para valores dados de C DO, K, W y S (para una aeronave dada) para varias altitudes como se muestra en el siguiente ejemplo.
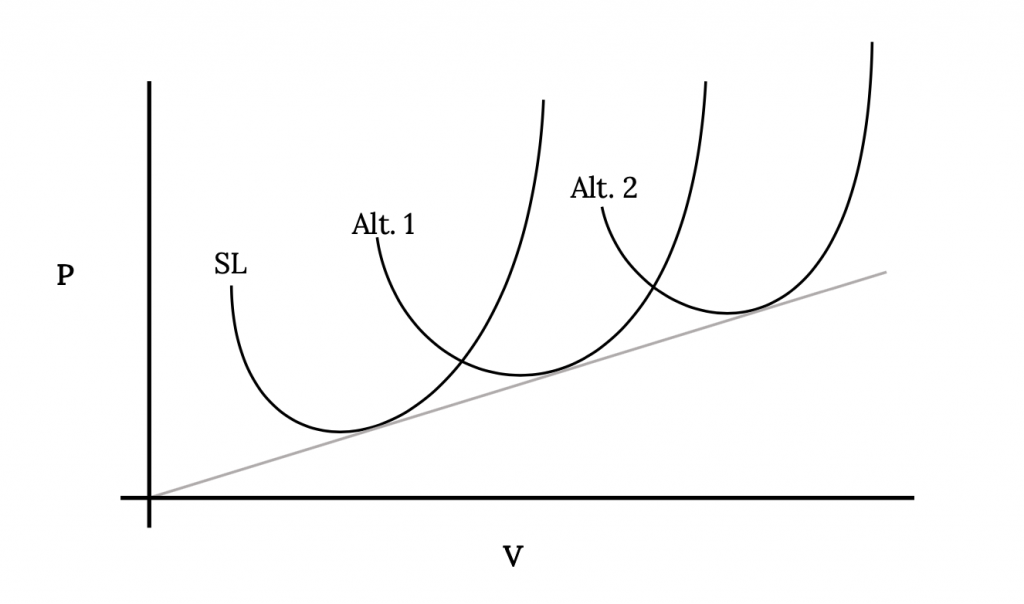
Notaremos que los valores mínimos de potencia no serán los mismos en cada altitud. Recordando que los valores mínimos de arrastre fueron los mismos en todas las altitudes y que la potencia requerida es tiempos de arrastre velocidad, es lógico que el valor mínimo de potencia aumente linealmente con la velocidad. Deberíamos ser capaces de trazar una línea recta desde el origen a través de los puntos mínimos de potencia requeridos en cada altitud.
La potencia mínima requerida en vuelo recto y nivelado puede, por supuesto, ser tomada de parcelas como la anterior. También nos gustaría determinar los valores de elevación y coeficiente de arrastre que resultan en la potencia mínima requerida tal como lo hicimos para el arrastre mínimo.
Se podría suponer al principio que la potencia mínima para una aeronave dada ocurre en las mismas condiciones que las de arrastre mínimo. Esto, por supuesto, no es cierto debido a la dependencia añadida de la potencia en la velocidad. Podemos comenzar a comprender los parámetros que influyen en la potencia mínima requerida volviendo nuevamente a nuestras ecuaciones simples de equilibrio de fuerzas para vuelo recto y nivelado:
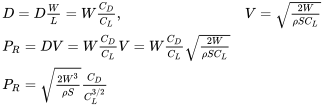
Así, para una aeronave dada (peso y área de ala) y altitud (densidad), la potencia mínima requerida para un vuelo recto y nivelado ocurre cuando el coeficiente de arrastre dividido por el coeficiente de sustentación a los dos tercios de potencia es mínimo.
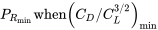
Suponiendo un polar de arrastre parabólico, podemos escribir una ecuación para la relación de coeficientes anterior y tomar su derivada con respecto al coeficiente de sustentación (ya que C L es lineal con ángulo de ataque esto es lo mismo que buscar un máximo sobre el rango de ángulo de ataque) y establecerlo igual a cero a encontrar un máximo.
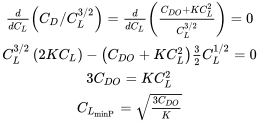
Tenga en cuenta que
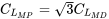
El coeficiente de sustentación para la potencia mínima requerida es mayor (1.732 veces) que para las condiciones mínimas de arrastre.
Conociendo el coeficiente de elevación para la potencia mínima requerida es fácil encontrar la velocidad a la que esto ocurrirá.
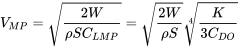
Tenga en cuenta que la velocidad para la potencia mínima requerida es menor que la de la mínima resistencia.
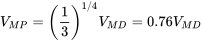
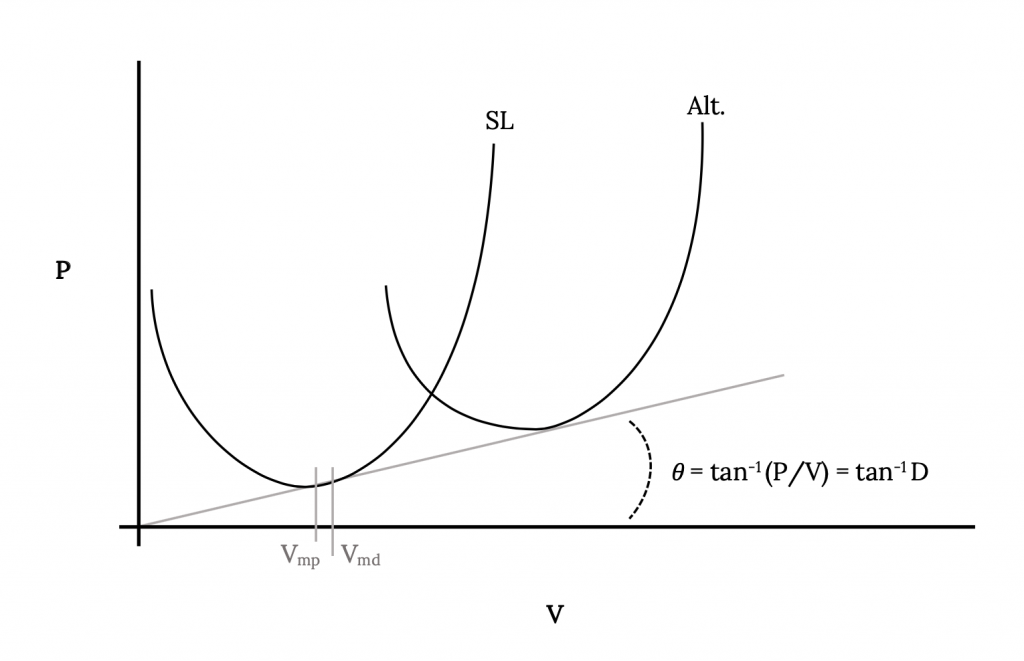
La potencia mínima requerida y las velocidades mínimas de arrastre se pueden encontrar gráficamente a partir de la gráfica de potencia requerida. La potencia mínima obviamente está en la parte inferior de la curva. Al darse cuenta de que el arrastre es el poder dividido por la velocidad y que una línea trazada desde el origen hasta cualquier punto de la curva de potencia está en un ángulo con respecto al eje de velocidad cuya tangente es la potencia dividida por la velocidad, entonces la línea que toca la curva con el ángulo más pequeño debe tocarla en la condición mínima de arrastre. A partir de esto podemos determinar gráficamente la potencia y velocidad al mínimo arrastre y luego dividir el primero por el segundo para obtener el arrastre mínimo. Tenga en cuenta que este método gráfico funciona incluso para casos de arrastre no parabólicos. Ya que sabemos que todas las altitudes dan el mismo arrastre mínimo, todas las curvas de potencia requeridas para las diversas altitudes serán tangentes a esta misma línea siendo el punto de tangencia el punto de arrastre mínimo.
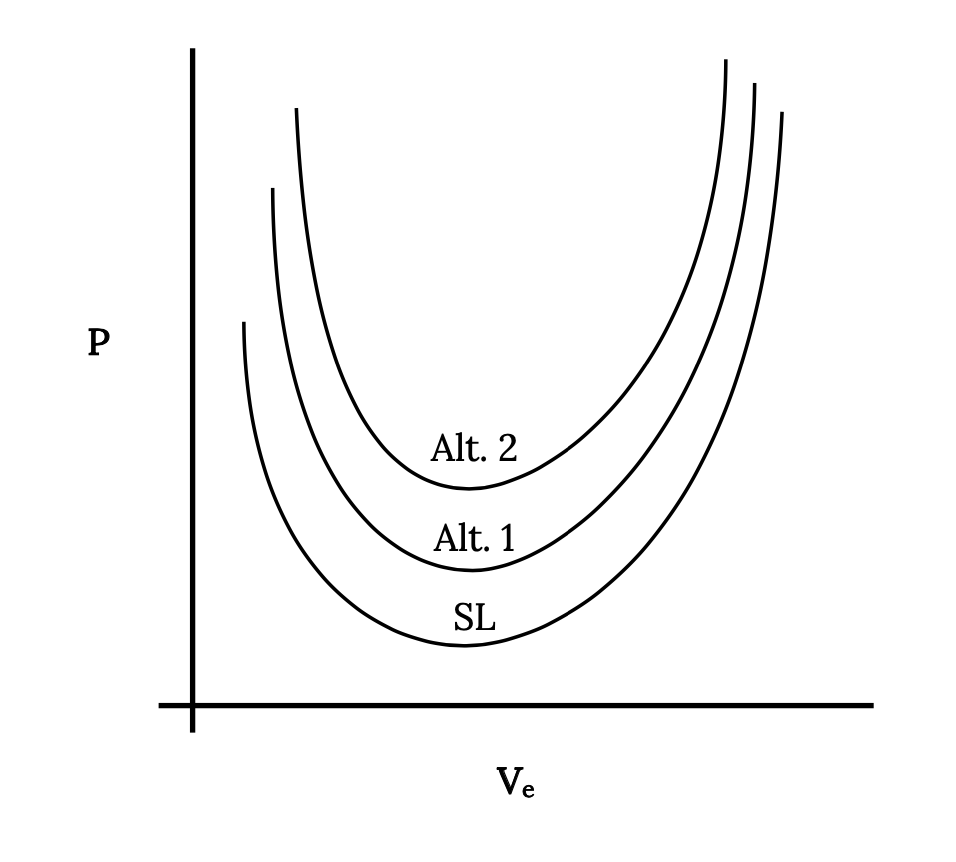
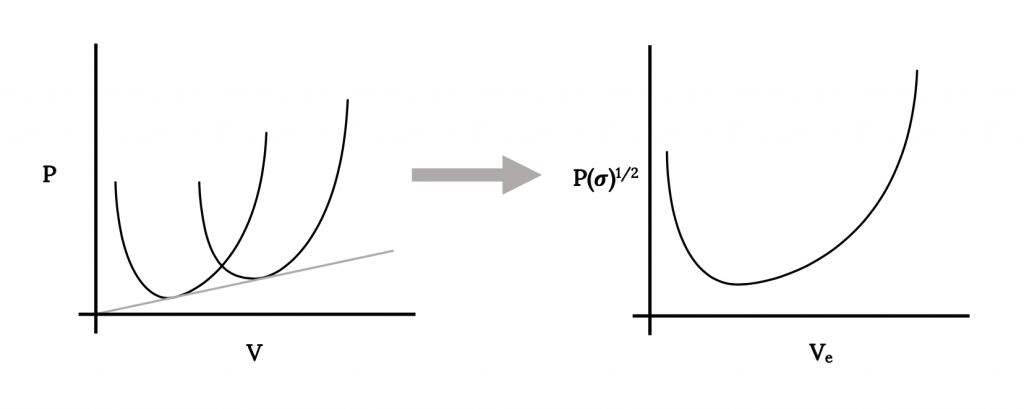
Otro elemento a considerar al observar la representación gráfica de la potencia requerida es la condición necesaria para colapsar los datos de todas las altitudes a una sola curva. En el caso del empuje requerido o arrastre esto se logró simplemente trazando la resistencia en términos de velocidad equivalente a nivel del mar. Eso no funcionará en este caso ya que la curva de potencia requerida para cada altitud tiene un mínimo diferente. Trazar todos los datos en términos de Ve comprimiría las curvas con respecto a la velocidad pero no con respecto a la potencia. El resultado sería una trama como la siguiente:
Sabiendo que la potencia requerida es la velocidad de los tiempos de arrastre, podemos relacionar la potencia requerida a nivel del mar con esa a cualquier altitud.
o
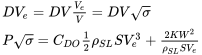
El resultado es que para colapsar todos los datos de potencia requerida a una sola curva debemos trazar la potencia multiplicada por la raíz cuadrada de sigma versus velocidad equivalente al nivel del mar. Esta, por lo tanto, será nuestra convención para trazar datos de potencia.
4.17 Revisión
En lo anterior encontramos las siguientes ecuaciones para la determinación de condiciones de potencia mínima requerida:
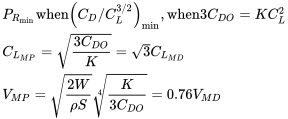
También podemos escribir
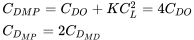
Por lo tanto, el coeficiente de arrastre para las condiciones de potencia mínima requerida es el doble que para el arrastre mínimo. También podemos escribir
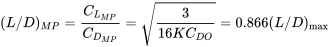
Dado que las condiciones mínimas requeridas de potencia son importantes y serán utilizadas posteriormente para encontrar otros parámetros de desempeño, se sugiere que el alumno escriba las relaciones anteriores en una página especial en sus notas para facilitar su referencia.
Posteriormente echaremos un vistazo completo a tratar con la energía disponible. Si conocemos la potencia disponible podemos, por supuesto, escribir una ecuación con la potencia requerida equiparada a la potencia disponible y resolver para las velocidades de vuelo máximas y mínimas rectas y niveladas tanto como hicimos con las ecuaciones de empuje. Las ecuaciones de potencia, sin embargo, no son tan simples como las ecuaciones de empuje debido a su dependencia del cubo de la velocidad. A menudo la mejor solución es una itterativa.
Si la potencia disponible de un motor es constante (como se suele suponer para un motor de hélice) la relación que equipara la potencia disponible y la potencia requerida es
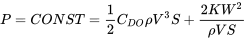
Para un motor a reacción donde el empuje se modela como una constante, la ecuación se reduce a la utilizada en la sección anterior sobre cálculos de rendimiento basados en Thrust.
EJEMPLO 4.3
Para el mismo avión de 3000 lb utilizado en ejemplos anteriores calcular la velocidad para la potencia mínima.
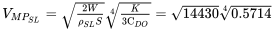
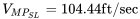
- Se sugiere que el alumno realice parcelas de la potencia requerida para vuelo recto y nivelado a nivel del mar y a 10,000 pies de altitud y verificar gráficamente los valores calculados anteriormente.
- También se sugiere que a partir de estas parcelas el alumno encuentre las velocidades para el arrastre mínimo y las compare con las encontradas anteriormente.
4.18 Resumen
Este capítulo ha mirado varios elementos de rendimiento en vuelo recto y nivelado. Se propuso un modelo simple para la variación de arrastre con velocidad (el polar parabólico de arrastre) y éste se utilizó para desarrollar ecuaciones para los cálculos de las condiciones mínimas de vuelo de arrastre y para encontrar velocidades de vuelo máximas y mínimas a diversas altitudes. También se destacaron los métodos gráficos y cabe señalar nuevamente que estos métodos gráficos funcionarán independientemente del modelo de arrastre utilizado.
Se sugiere fuertemente que el estudiante se acostumbre a dibujar una gráfica de las curvas de empuje y/o potencia versus velocidad como ayuda de visualización para cada problema, incluso si la solución utilizada es completamente analítica. Dichos bocetos pueden ser una herramienta valiosa para desarrollar una sensación física para el problema y su solución.
Tarea 4
1. Utilice el teorema del momentum para encontrar el empuje para un motor a reacción donde se conocen las siguientes condiciones:
| velocidad de entrada | 300 fps |
| densidad de flujo de entrada | 0.0023 sl/ft^3 |
| área de entrada | 4 pies^2 |
| velocidad de flujo de salida | 1800 fps |
| densidad de flujo de salida | desconocido |
| zona de salida | 2 pies^2 |
| caudal de combustible | 5lb_m/seg |
Asumir un flujo constante y que las presiones de entrada y salida son atmosféricas.
2. Encontramos que el empuje de una hélice podría describirse mediante la ecuación T = T 0 — aV 2. Con base en esta ecuación, describa cómo configuraría un experimento simple de túnel de viento para determinar los valores para T 0 y a para un modelo de motor de avión. Suponga que tiene acceso a un túnel de viento, un tubo pitot-estático, un manómetro de tubo en U y una célula de carga que medirá el empuje. Dibuja un boceto de tu experimento.
Referencias
Figura 4.1: Gris Kindred (2021). “Equilibrio de Fuerza Estática en Vuelo Recto y Nivel”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.1_20210804
Figura 4.2: Gris Kindred (2021). “Diferentes Tipos de Puestos”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.2_20210804
Figura 4.3: Gris Kindred (2021). “Parte del arrastre aumenta con la velocidad al cuadrado”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.3_20210804
Figura 4.4: Gris Kindred (2021). “Parte del arrastre disminuye con la velocidad al cuadrado”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.4_20210804
Figura 4.5: Gris Kindred (2021). “Variación Total de Arrastre Con Velocidad”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.5_20210804
Figura 4.6: Gris Kindred (2021). “Efecto de altitud en la variación de arrastre”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Recuperado a partir de https://archive.org/details/4.6_20210804
Figura 4.7: Gris Kindred (2021). “Velocidad de arrastre versus equivalente al nivel del mar (indicada)”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.7_20210804
Figura 4.8: Gris Kindred (2021). “Método Gráfico para Determinar Condiciones Mínimas de Arrastre”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.8_20210805
Figura 4.9: Gris Kindred (2021). “Variación de Empuje y Arrastre Con Velocidad”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.9_20210805
Figura 4.10: Gris Kindred (2021). “Velocidades mínimas y máximas para vuelo recto y nivelado”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.10_20210805
Figura 4.11: Gris Kindred (2021). “Variación de empuje con altitud vs velocidad equivalente al nivel del mar”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.11_20210805
Figura 4.12: Gris Kindred (2021). “Envolvente de velocidad de vuelo recto y nivelado con altitud”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.12_20210805
Figura 4.13: Gris Kindred (2021). “Verdadero Velocidad Aérea Máxima Versus Altitud”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.13_20210805
Figura 4.14: Gris Kindred (2021). “Solución Gráfica para Empuje Constante a Cada Altitud”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.14_20210805
Figura 4.15: Gris Kindred (2021). “La potencia disponible varía linealmente con la velocidad”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.15_20210805
Figura 4.16: Gris Kindred (2021). “Potencia requerida y variación disponible con altitud”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.16_20210805
Figura 4.17: Gris Kindred (2021). “Potencia requerida Variación Con Altitud”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.17_20210805
Figura 4.18: Gris Kindred (2021). “Determinación Gráfica de Velocidad Mínima de Arrastre y Potencia Mínima”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.18_20210805
Figura 4.19: Gris Kindred (2021). “Parcela de Potencia Requerida vs Velocidad Equivalente a Nivel del Mar”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.19_20210805
Figura 4.20: Gris Kindred (2021). “Compresión de datos de potencia a una sola curva”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/4.20_20210805
<! — pb_fixme —><! — pb_fixme —>


