5: Cambio de Altitud - Subida y Guía
( \newcommand{\kernel}{\mathrm{null}\,}\)
Capítulo 5. Cambio de Altitud: Subida y Guía
Introducción
A través de las curvas básicas de potencia y rendimiento de empuje consideradas en el último capítulo hemos podido investigar el rendimiento de vuelo recto y nivelado de una aeronave. Ahora debemos agregar otra dimensión a nuestro estudio del rendimiento, la de los cambios de altitud. Sabemos que a partir de los datos de recta y nivel podemos determinar la altitud máxima teórica, o techo, para una aeronave determinada. La pregunta que hay que responder ahora es ¿cómo conseguimos el avión de una altitud a otra? Esta discusión debe incluir la investigación de las posibles tasas de ascenso y descenso, la distancia sobre el suelo necesaria para escalar una altitud determinada y el alcance de la aeronave en un planeamiento. ¿Qué tan rápido puedo llegar de la altitud A a la altitud B? ¿Hasta dónde puedo deslizarme después de que mi motor falle? Si me quito a 600 pies del final de la pista, ¿puedo despejar los árboles de adelante?
Para mirar los cambios de altitud necesitamos pensar en términos de cambios energéticos. En ascenso estamos convirtiendo la energía cinética e interna (del motor) en un aumento de la energía potencial. En un planeo estamos convirtiendo la energía potencial en velocidad (energía cinética) que nos dará la elevación necesaria para volar.
Una de las preguntas anteriores involucró la tasa de ascenso. En la escalada, la aeronave está aumentando su energía potencial. La tasa de ascenso implica entonces el cambio de energía potencial en un tiempo dado. El motor proporciona la energía necesaria para subir y la salida de energía del motor por unidad de tiempo es potencia (trabajo por unidad de tiempo). Somos conscientes de que se requiere cierta cantidad de potencia para un vuelo recto y nivelado a una velocidad determinada. Para escalar a esa misma velocidad entonces se requiere potencia extra y la cantidad de esa potencia extra determinará la velocidad a la que ocurrirá la subida. La velocidad máxima de ascenso a una velocidad determinada dependerá entonces de la diferencia entre la potencia disponible del motor a esa velocidad y la potencia requerida para el vuelo recto y nivelado. Esto se puede determinar a partir de la información de rendimiento de potencia estudiada en el último capítulo.
El concepto de agregar potencia para aumentar la altitud (ascenso) no suele ser intuitivo. La mayoría de nosotros estamos condicionados por la experiencia con autos, embarcaciones y bicicletas para pensar en el aumento de velocidad como consecuencia de agregar potencia. Estos, por supuesto, son vehículos limitados a la altitud de la carretera o superficie del agua. Sin embargo, si pensamos en un automóvil que va sobre una colina, el proceso no es difícil de entender. Si un automóvil viaja a, digamos, 55 mph (¡ya que ninguno de nosotros pensaría en conducir a velocidades superiores al límite!) y arrancamos una colina manteniendo firme el acelerador (acelerador), el auto desacelerará a medida que sube la colina, cambiando la energía cinética por energía potencial. Para mantener nuestras 55 mph (manteniendo constante la energía cinética) a medida que nos movemos por la colina debemos sumar potencia. Lo mismo ocurre en una aeronave.
Una de las cosas más difíciles para un instructor de vuelo para enseñar a un nuevo piloto es que el acelerador controla la altitud y la palanca de control o yugo controla la velocidad. Esto, por supuesto, no del todo cierto ya que los dos controles se utilizan simultáneamente; sin embargo, esta es la analogía que mejor servirá al piloto en una situación difícil. Por ejemplo, en una aproximación al aterrizaje el piloto está intentando mantener un descenso constante hacia la pista. Si una corriente descendente repentina provoca una pérdida de altitud, el piloto debe tomar medidas inmediatas para recuperar la altitud perdida o correr el riesgo de un encuentro no planificado con el suelo corto de la pista. Tirar hacia atrás en el control para subir la nariz de la aeronave es la respuesta instintiva más común ya que la aeronave está descendiendo con la nariz hacia abajo. Esto, sin embargo, simplemente aumentará el ángulo de ataque y dará como resultado una reducción de la velocidad, lo que posiblemente conducirá a una parada y, ciertamente, a una mayor pérdida de sustentación y altitud. La respuesta adecuada, sumar potencia, dará como resultado una subida para recuperarse de la pérdida de altitud. El control final de la aeronave en tal circunstancia requerirá el uso coordinado de ambos controles para regular tanto la velocidad como la altitud durante esta fase de vuelo más difícil.
El piloto en la situación anterior no va a dejar de pensar en la potencia disponible de ella o de su aeronave o en las curvas de rendimiento de potencia requerida. Este es el trabajo del ingeniero que diseña el avión para poder satisfacer las necesidades del piloto en tal situación. Este es nuestro trabajo en las secciones que siguen. En este estudio debemos agregar un ángulo a nuestra ilustración anterior del equilibrio de fuerzas en el avión. Este será el ángulo de ascenso, θ, que se considerará positivo en una subida y negativo en un planeo o descenso.
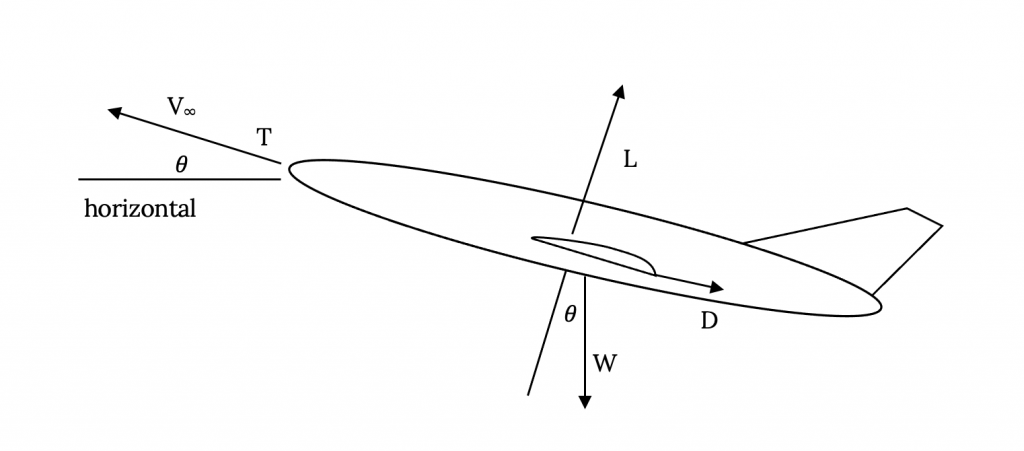
Sumando las fuerzas en la figura anterior a lo largo del eje de empuje encontramos:

Pero esta ecuación es una relación estática que no permite la aceleración; es decir, no permite un cambio en la energía cinética. Para considerar todas las fuerzas que puedan estar involucradas en la subida también debemos considerar la aceleración, por lo que la ecuación anterior se convierte en:
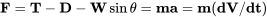
Si reorganizamos esta ecuación y dividimos por peso (mg) obtenemos:
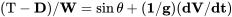
Entonces, multiplicando por velocidad, tenemos:
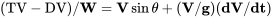
o
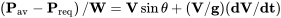
Ahora, V sin θ resulta ser la velocidad vertical o la velocidad de ascenso como se muestra en la Figura 5.2.
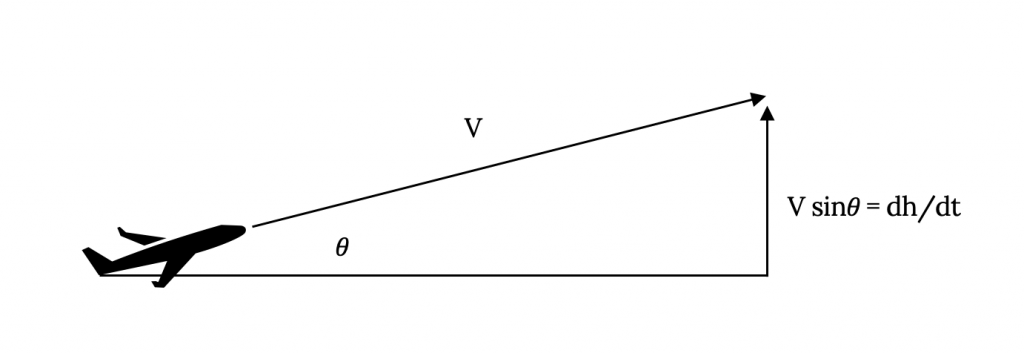
Entonces tenemos (P av — P req)/W = dh/dt + (V/g) (dV/dt) (dV/dt).
Y, podemos reorganizar esto para dar
dh/dt = (P av — P req)/W — (V/g) (dV/dt).
Es común referirse al primer término entre paréntesis a la derecha en esta ecuación como el exceso de potencia. Cuando el exceso de potencia se divide por el peso como en la ecuación anterior se convierte en el exceso de potencia específico, P s.
P s = (P av — P req)/W.
Ahora, volviendo a una forma anterior de la ecuación, podemos escribir
P s = dh/dt + (V/g) (dV/dt)
Esta es una relación muy importante que nos dice que podemos usar nuestro exceso de potencia (la potencia por encima y por encima de la necesaria para un vuelo recto y nivelado) para subir (dh/dt) o para cambiar nuestra velocidad (acelerar o desacelerar) o para hacer ambas cosas al mismo tiempo. También podemos convertir velocidad a altitud o altitud en velocidad.
En situaciones reales, un piloto iniciará una subida tanto aumentando el acelerador (agregando potencia del motor) como disminuyendo la velocidad, lo que significa que tanto la potencia del motor como la energía cinética se están convirtiendo en velocidad de ascenso. En descenso, el piloto a menudo reducirá la configuración de potencia del avión (acelerador) para que no toda la disminución de la energía potencial se destine a aumentar la velocidad sino que algo se destine a la energía necesaria para mantener el vuelo de elevación.
En realidad, ¿cuánta ganancia se puede lograr convirtiendo la energía cinética en energía potencial sin cambiar la configuración de potencia del motor? Podemos encontrar esto con bastante facilidad si miramos directamente un intercambio de este tipo
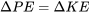
o
dando
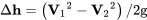
Usando esto podemos encontrar que para una aeronave que vuela 200 mph y desacelera a 160 mph durante una subida inicial, la ganancia de altitud al intercambiar energía cinética por energía potencial llega a 483 pies. Esto es bastante pequeño si uno está pensando en hacer una subida de 5000 pies pero puede ser útil en términos de maniobras de evitación de emergencia. Por otro lado, la misma ecuación mostrará que un avión que vuela 500 mph puede ganar más de 5000 pies de altitud al desacelerar a 300 mph y si uno está mirando un avión de velocidad supersónica esta cinética para el intercambio de energía potencial se vuelve muy significativa en la contabilidad de las capacidades de ascenso y descenso. Tenga en cuenta que la masa de la aeronave no está en la ecuación anterior.
En un capítulo posterior volveremos a los conceptos de exceso de energía específica y de velocidad de negociación para altitud o visa-versa. Por el momento veremos el caso más sencillo de vuelo no acelerado y asumiremos que todas las subidas y descensos se realizan a velocidad constante y que la tasa de cambio de altitud es sólo una función del uso del exceso de potencia. Esto supondrá esencialmente que la altitud a ganar o perder cambiando nuestra velocidad aérea es insignificante.
Comenzaremos nuestra mirada “estática” al cambio de altitud mirando el vuelo en planeamiento con cero potencia disponible.
5.1 Vuelo en planeamiento
El primer caso que consideraremos será el caso simple de descenso no motorizado, o planeo. Esta es una situación de rendimiento muy importante para una aeronave ya que todas las aeronaves son susceptibles a fallas en el motor. Una de las primeras cosas que se le enseña a hacer a un estudiante piloto es a manejar correctamente un “motor fuera” en su avión; cómo configurar la mejor velocidad para optimizar la velocidad de descenso a fin de permitir el máximo tiempo para pedir ayuda, reiniciar el motor, prepararse para un aterrizaje de emergencia, etc. para algunas aeronaves por supuesto , el deslizamiento sin potencia es normal. Planos de vela y alas delta vienen a la mente de inmediato pero también se debe considerar que el Transbordador Espacial no es más que un avión con un “motor fuera” en su descenso de órbita a aterrizaje!
En un planeo sin propulsión solo hay tres fuerzas que actúan sobre la aeronave, elevación, arrastre y peso. Estas fuerzas deben alcanzar un estado de equilibrio en el planeo. Corresponde al piloto asegurarse de que el equilibrio alcanzado sea óptimo para la supervivencia y, en la mayoría de los aviones, le corresponde al diseñador de aviones hacer el avión para que busque por sí solo una posición de equilibrio razonable. ¡El avión que se para y entra en una vuelta tras la pérdida de un motor no será muy popular entre la mayoría de los pilotos! Ahora debemos determinar cuáles son esas condiciones óptimas.
Usando la Figura 5.1 y usando un empuje de cero podemos escribir las siguientes dos relaciones simples de equilibrio de fuerzas en las direcciones de elevación y arrastre:
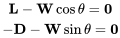
Dividiendo la segunda ecuación por la primera da
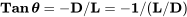
Ahí está ese término otra vez, L/D!
Esto nos dice un hecho muy simple y muy importante: el ángulo de deslizamiento depende únicamente de la relación elevación-arrastre.
El ángulo de deslizamiento es:
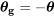
y
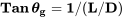
Algo parece mal aquí. ¿Significa esto que el ángulo de planeo no tiene nada que ver con el peso de la aeronave? Seguro que parece que un avión pesado no se deslizaría como uno ligero. ¿Un Boeing 747 se deslizará igual que un Cessna 152? ¿Qué pasa con el Transbordador Espacial?
Sí, la ecuación no contiene el peso de la aeronave a pesar de que estaba en las ecuaciones de balance de fuerzas originales. El ángulo de deslizamiento depende únicamente de la relación elevación-arrastre y esa relación depende de parámetros como C D0, K y e como se discutió en el último capítulo.
Pero, ¿no significa que el hecho de que deba haber suficiente levantamiento para soportar el peso (o al menos la mayor parte) significa que el peso realmente es un factor? Realmente no, ya que el arrastre también se ve como una función del peso y en la relación de elevación-arrastre, el peso “divide” de la relación. Un Boeing 747 de hecho puede deslizarse así como un Cessna 152.
Entonces, ¿cuáles son nuestras preocupaciones en un planeo? Esencialmente queremos saber hasta dónde puede deslizarse la aeronave (alcance) y cuánto tiempo tardará en llegar al suelo (resistencia).
5.1.1 Rango en un Deslizamiento
Veremos el rango asumiendo una ausencia de cualquier viento natural. Este es, por supuesto, raramente el caso en la vida real pero es el caso más fácil de examinar para nosotros. También asumiremos un planeo constante, es decir, que el piloto ha establecido (o recortado) la aeronave de tal manera que mantendrá la velocidad aerodinámica y el ángulo de planeo indicados seleccionados durante todo el descenso. La geometría de la situación es bastante simple como se muestra a continuación.
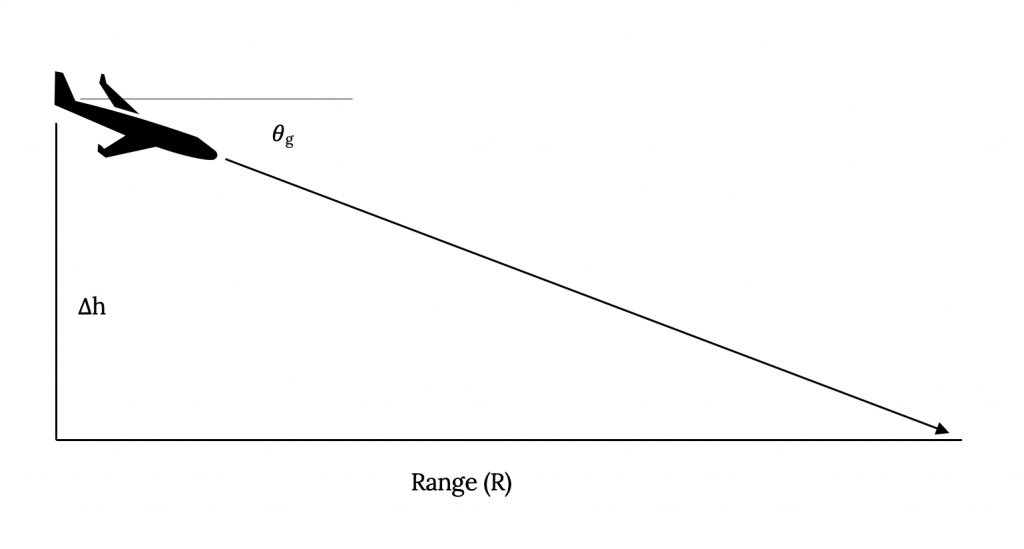
De la figura queda claro que el ángulo de planeo es el arco-tangente del cambio de altitud dividido por el rango.
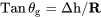
Esto da una gama de:
y dado que la tangente del ángulo de deslizamiento es simplemente la relación de elevación a arrastre, tenemos
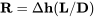
El rango máximo en un deslizamiento ocurre en la relación máxima — a arrastre; es decir, ¡en condiciones mínimas de arrastre! Ya sabemos cómo encontrar algo que podamos desear saber sobre las condiciones mínimas de arrastre, así que sabemos cómo determinar las condiciones para el rango máximo en un planeo sin motor.
Para el piloto esto significa que debe, al perder la potencia del motor, recortar la aeronave para que se deslice a la velocidad aerodinámica indicada (equivalente al nivel del mar) para un arrastre mínimo, velocidad que el ingeniero ha proporcionado en el manual del propietario de la aeronave, si se desea un alcance máximo. El piloto volaría entonces la aeronave para mantener la velocidad deseada en el planeo.
Por lo general, el alcance máximo no es el objetivo más deseable en una situación de “motor fuera”. La mejor solución suele ser optimizar el tiempo antes del “encuentro terrestre” (¡ojalá un aterrizaje!). Esto significa ir por una tasa mínima de descenso en lugar de un rango máximo. Esta es, de nuevo, una de esas cosas que quizás no sean intuitivas para la mayoría de la gente, incluso para los pilotos, y hay muchos casos en los que los aviones se han estrellado ya que los pilotos intentaron sin éxito estirar su alcance después de que un motor falla. El viento, que no se incluyó en los cálculos anteriores, puede cortar el rango a cero o puede mejorarlo. Las distancias son difíciles de juzgar desde el aire. A los estudiantes pilotos se les enseña que en una situación de “motor fuera” es el momento que debe optimizarse más que el rango. El piloto necesita conocer la velocidad aérea para la tasa mínima de descenso en lugar de para el alcance máximo con el fin de recortar la aeronave para un descenso que permita el tiempo máximo para intentar reiniciar el motor, para prepararse para un aterrizaje de emergencia, para recibir ayuda por radio, etc. Esto significa que estamos interesados en la tasa de descenso.
Mirar la tasa de descenso es un poco más complicado que mirar el rango. Consideraremos dos casos, el caso de ángulo de deslizamiento pequeño donde podemos hacer algunas suposiciones simplificadoras y el caso general o de ángulo grande. Al mirar el caso de ángulo pequeño usaremos la suposición matemática habitual de que el coseno de un ángulo está lo suficientemente cerca de la unidad como para que podamos aproximarlo como uno solo. El límite habitual de esta suposición es de unos 5 grados ya que una comprobación en nuestra calculadora mostrará que cos 5º = 0.99619. Sin embargo, nuestro ángulo de interés es el ángulo de deslizamiento que ya sabemos que es igual a la tangente de arco de D/L; también nos gustaría suponer que el seno de ese ángulo es aproximadamente igual a su tangente. Debido a esto, estiraremos la aplicabilidad de la racionalización de ángulos pequeños para incluir ángulos de deslizamiento de hasta aproximadamente 15 grados.
(A los quince grados el coseno es 0.9659, por lo que todavía estamos dentro del 5% a nuestra meta de coseno = 1.0. Esto suele ser bastante bueno en el mundo real. También la tangente de quince grados es 0.2679 mientras que el seno es 0.2588, haciendo que nuestra suposición seno=tangente sea buena con menos de 4% de error.)
Un resultado útil de la suposición de ángulo pequeño es que nos permitirá asumir además que la elevación es aproximadamente igual al peso. Desde que tuvimos
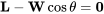
y si
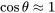
entonces
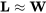
Esto podría denominarse vuelo “cuasi-nivel”. La principal ventaja de esta suposición es que nos permite continuar relacionando la velocidad con el peso a través de
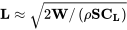
a pesar de que el vuelo no es realmente recto y nivelado.
Ahora queremos comenzar a mirar la tasa de cambio de altitud, dh/dt o h. Esta es la tasa de ascenso cuando se define en términos de un cambio positivo de altitud como se muestra en la Figura 5.2.
De la Figura 5.2 vemos que la velocidad de ascenso es igual a la velocidad aérea del avión multiplicada por el seno del ángulo de ascenso. Refiriéndose a nuestras ecuaciones anteriores de balance de fuerzas para el caso de deslizamiento (sin empuje) podemos escribir
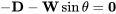
o
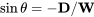
y usando la suposición de ángulo pequeño de que el peso es aproximadamente igual a la elevación da
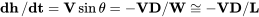
Cambiar a una forma que utiliza los coeficientes de fuerza
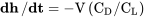
Ahora use la otra suposición de ángulo pequeño para la velocidad
![V [2W/ (ρSCL)] 1/2](https://eng.libretexts.org/@api/deki/files/49265/4d07a12aa96624feb25ca58659f13cd2.png)
tenemos
![dh/dt [2W/ (ρSCL)] 1/2 [CD/CL]](https://eng.libretexts.org/@api/deki/files/49266/121f47ba5d0c9c3c31b8b5d871c8db2a.png)
o finalmente
![dh/dt [2W/ (ρS)] 1/2 [CD/CL3/2]](https://eng.libretexts.org/@api/deki/files/49267/f7caa76b8b7b36b2ce22cf950f543052.png)
Tenga en cuenta que esta es una tasa negativa de ascenso ya que estamos viendo el caso de planeo o descenso (asumimos que no hay empuje).
De lo anterior es obvio que para la tasa mínima de descenso para una aeronave dada y altitud se producirá cuando C D /C L 3/2 esté en un mínimo. Mirando hacia atrás a nuestro estudio del poder en el capítulo anterior encontramos que esta es la misma condición que se encuentra para la potencia mínima requerida.
En revisión, hemos encontrado las condiciones necesarias para el vuelo en un planeo sin motor para dos casos óptimos, tasa mínima de descenso y alcance máximo sin viento. Estos se encuentran que ocurren cuando la aeronave descendente se recorta para mantener una velocidad aerodinámica indicada para las condiciones mínimas de potencia requeridas y para la mínima resistencia, respectivamente. Sabemos todo sobre ambas condiciones a partir de la discusión del capítulo anterior.
Hemos encontrado que para cualquier planeo, el rango sin viento es
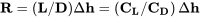
y para ángulos de deslizamiento de quince grados o menos la tasa de descenso es
![dh/dt [2W/ (ρS)] 1/2 [CD/CL3/2]](https://eng.libretexts.org/@api/deki/files/49267/f7caa76b8b7b36b2ce22cf950f543052.png)
Estos se pueden utilizar para encontrar el rango y la velocidad de descenso para cualquier condición de deslizamiento donde conocemos los coeficientes de elevación y arrastre apropiados (ángulo de ataque) y no se limitan a los casos óptimos. Además, sabemos que para optimizar el alcance necesitamos volar en condiciones mínimas de arrastre mientras que para una tasa mínima de descenso, necesitamos volar en las condiciones para la potencia mínima requerida.
La mayoría de las aeronaves en un planeo satisfarán la suposición de ángulo pequeño de quince grados utilizada en lo anterior. Algunos, como el Transbordador Espacial, no lo harán. Por lo tanto, vale la pena retroceder y considerar brevemente el caso de los ángulos de deslizamiento pronunciados. Este es, por supuesto, el caso general sin la suposición de ángulo pequeño. Debemos usar las ecuaciones de balance de fuerzas tal como se desarrollan sin las aproximaciones. Estos se convierten
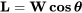
y
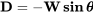
La ecuación de velocidad no puede asumir vuelo recto y nivelado y la primera de las dos ecuaciones anteriores debe usarse para insertar el peso de la aeronave en la relación.
o
![V= [2W/ρSCL] 1/2 [cosθ] 1/2](https://eng.libretexts.org/@api/deki/files/49272/5fc9486229bc77f5b0b16d02c9f592aa.png)
La definición del ángulo de deslizamiento no ha cambiado
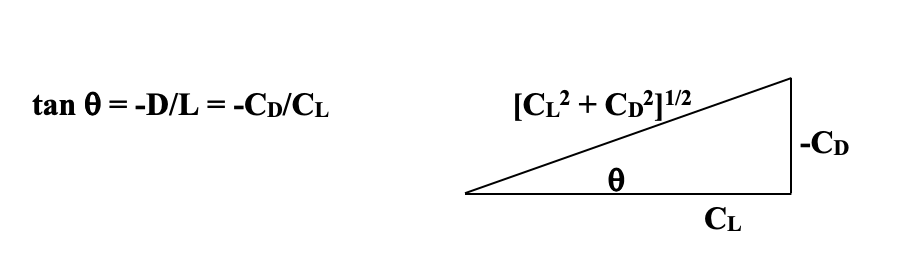
y podemos usar esta relación con alguna trigonometría simple para encontrar una relación entre el coseno del ángulo de deslizamiento o ascenso y los coeficientes de elevación y arrastre.
![SINθ=−CD/ [CL2+CD2] 1/2, COsθ=CL/ [CL2+CD2] 1/2](https://eng.libretexts.org/@api/deki/files/49274/4670c8636d19b651d55ecb2761793115.png)
La ecuación de la tasa de ascenso (tasa de descenso) ahora se convierte en
o
![dh/dt= [2W/ (ρSCL)] 1/2 {CD/ [CL2+CD2] 3/4}](https://eng.libretexts.org/@api/deki/files/49276/d76dfbbf27846e2cf09b5b716cab1889.png)
Esta es una relación que determinará la velocidad de descenso para cualquier ángulo de deslizamiento. Se observa que esta ecuación no es realmente más complicada matemáticamente que la encontrada usando la aproximación del ángulo de deslizamiento pequeño. La diferencia es que ahora no existe correlación entre la tasa mínima de descenso y la condición para la potencia mínima requerida.
5.2 Tiempo para descender
Usando la tasa de descenso y el cambio de altitud
es posible determinar el tiempo requerido para ese descenso.
dt = dh/(dh/dt)
Si la tasa de descenso es constante esto puede llegar a ser
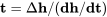
En realidad ya hemos demostrado que tanto para los casos generales como para los de ángulo pequeño la velocidad de descenso no es constante sino que depende de la altitud ya que es función de la densidad. Por lo tanto, la ecuación completa sería
![t=−h1H2DH/2WρsCD (CL2+CD2) 3/4]](https://eng.libretexts.org/@api/deki/files/49279/94fe786beb717e55295bfed755ddd466.png)
y mediante el uso de las ecuaciones para la variación de densidad en la atmósfera estándar se podría insertar la densidad en función de h para dar una ecuación general para el tiempo de descenso. Sin embargo, para obtener una imagen más simple del problema del tiempo para descender asumiremos que se puede utilizar un enfoque incremental donde la densidad, y por lo tanto la tasa de descenso, se puede suponer constante en incrementos razonablemente pequeños de altitud durante el descenso. Por ejemplo, sobre un incremento de altitud de 1000 pies podemos basar nuestros cálculos en la densidad (tasa de descenso) a medio camino entre la altitud superior e inferior sin introducir mucho error. Esto se puede repetir incrementalmente para encontrar el tiempo de descenso sobre cambios de altitud mayores. Algunos ejemplos simples podrían ayudar a ilustrar este proceso.
EJEMPLO 5.1
Un velero pesa mil libras y tiene una carga de ala (W/S) de 12.5 libras por pie cuadrado con un polar de arrastre dado por
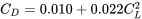
Encuentra el tiempo para deslizarte desde 1000 pies hasta el nivel del mar a una tasa mínima de descenso (tasa mínima de hundimiento).
Solución: La tasa mínima de disipación ocurre en condiciones para la potencia mínima requerida
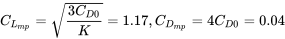
Podemos verificar la relación de elevación-arrastre resultante para determinar si las aproximaciones de ángulo pequeño son válidas
Así podemos encontrar la velocidad a partir de la ecuación “cuasi-nivel”
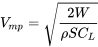
y usando la densidad para una altitud de 500 pies tenemos
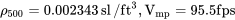
y la tasa de descenso se convierte
dando un tiempo para descender los 1000 pies
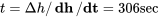
EJEMPLO 5.2
Considera el descenso del mismo velero desde una altitud mucho mayor. Podemos usar un descenso de 20,000 pies para investigar las imprecisiones de usar el enfoque incremental al problema del tiempo para descender. Supongamos que para obtener una primera conjetura para el momento de descender asumimos un solo incremento usando la densidad a 10,000 pies. Primero encontraremos una velocidad aérea
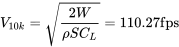
luego una tasa de descenso
dando un tiempo para el descenso de
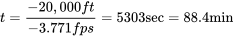
Debemos esperar una mayor precisión si utilizamos cuatro incrementos de 5000 pies cada uno, calculando velocidades y tasas de descenso a 17,500; 12,500; 7,500; y 2,500 altitudes de pies como se muestra en la siguiente tabla.
Tabla 5.1: Ejemplo 2
| h (pies) | h (media) (ft) | σ | V (fps) | DH/dt=VSINθ (fps) |
|---|---|---|---|---|
| 20,000-15,000 | 17,500 | 0.5793 | 124.49 | 4.258 |
| 15,000-10,000 | 12,500 | 0.6820 | 114.74 | 3.924 |
| 10,000-5,000 | 7,500 | 0.7982 | 106.05 | 33.627 |
| 5,000-NIVEL DEL MAR | 2,500 | 0.9288 | 98.32 | 3.363 |
V sL = 94.752 f |
||||
El tiempo total para descender se encuentra sumando los tiempos incrementales de cada uno de los descensos de 5000 pies.
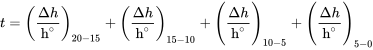
dando t = 5313.8 seg = 88.6 min
Esto da un tiempo para descender de 20,000 pies de 88.6 minutos, una diferencia de solo 0.2 minutos o 10.8 segundos de la solución bruta de incremento único.
¿Lo anterior muestra que tiene poco sentido romper el planeo en incrementos para encontrar el tiempo de descenso o simplemente que los incrementos elegidos fueron demasiado grandes para hacer mucha diferencia? Una solución de la ecuación integral “exacta” para el descenso de 20,000 pies dará como resultado un tiempo de descenso de 5426.5 segundos o 90.4 minutos. Solo hay una diferencia de dos minutos entre la solución “exacta” y la peor aproximación posible; ¡un error del 2%!
5.3 Vuelo de Escalada
Como se discutió anteriormente, la adición de potencia por encima de la requerida para el vuelo recto y nivelado a una velocidad dada hará posible ya sea un aumento de altitud o un cambio en la velocidad o ambos. Si la velocidad se mantiene constante mientras se agrega potencia (o empuje), el resultado será una subida. Dado que la escalada es mejor pensada como un aumento en la energía potencial, podemos analizarla mejor sobre una base de uso de energía como se refleja en la potencia o la adición de energía por unidad de tiempo. Para comenzar nuestra mirada a la subida podemos volver a la figura utilizada antes y otra vez escribir ecuaciones de equilibrio de fuerzas en las direcciones de levantamiento y arrastre, esta vez sumando el vector de empuje.
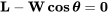
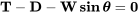
Cabe destacar que estamos asumiendo que la subida ocurre a velocidad constante. Esto significa físicamente que escalar es un intercambio directo de energía del motor por una ganancia de energía potencial. También significa que nuestras ecuaciones de balance de fuerzas suman a cero; es decir, son ecuaciones estáticas sin aceleración. Sin embargo, no nos limitaremos demasiado. Como todo buen ingeniero debería, vamos a dar un poco un poco al decir que estamos volando a “cuasi-estables: condiciones y toleramos aceleraciones muy pequeñas que son inevitables en vuelo real.
La relación de tasa de ascenso sigue siendo
A partir del balance de fuerza de Empuje/Arrastre arriba podemos escribir el ángulo de ascenso
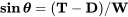
La tasa de ascenso es entonces
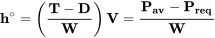
Tenga en cuenta desde lo anterior que el ángulo de ascenso depende de la cantidad de empuje en exceso mientras que la tasa de ascenso depende de la cantidad de exceso de potencia. No en vano, este es el mismo tipo de dependencia que encontramos en el caso del deslizamiento excepto que ahí hablamos de arrastre en lugar de empuje.
Dado que el ángulo de ascenso y la tasa de ascenso ambos pueden estar directamente relacionados con las curvas de rendimiento previamente discutidas para una aeronave, podemos echar un vistazo a estos parámetros ya que se relacionan con estas gráficas. A continuación se muestra una gráfica típica de empuje y arrastre (empuje requerido). A cualquier velocidad dada, la diferencia entre las curvas de empuje y arrastre se puede dividir por el peso de la aeronave para determinar el ángulo máximo posible de ascenso a esa velocidad utilizando la relación definida anteriormente. Por supuesto, a cualquier velocidad dada, no es necesario usar todo el exceso de empuje disponible para escalar si se desea un ángulo de ascenso más bajo. A medida que las curvas de empuje y arrastre se mueven juntas hacia la izquierda y hacia la derecha, el posible ángulo de ascenso se estrecha hacia cero a las velocidades donde el empuje es igual a arrastre.
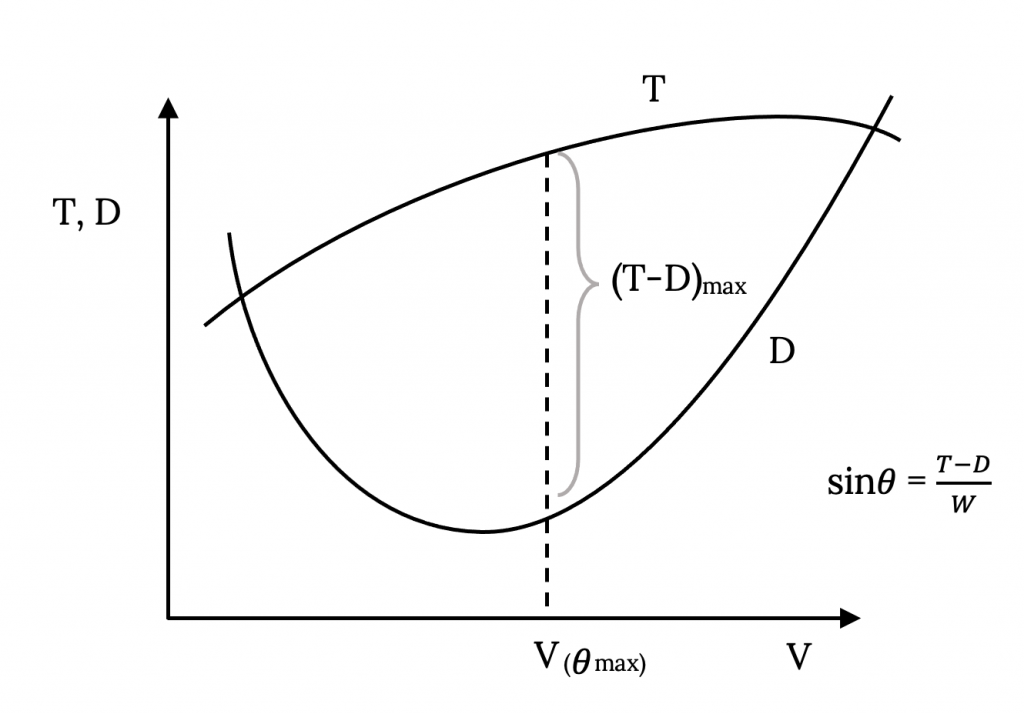
La velocidad donde se produce el ángulo máximo posible de ascenso es aquella para la cual la distancia vertical entre las curvas de empuje y arrastre es máxima. Esto se puede encontrar a partir de una gráfica de datos real simplemente usando una regla o un par de divisores para encontrar este máximo. También se podría encontrar analíticamente si se conocen relaciones funcionales para las curvas de empuje y arrastre tomando la derivada de la diferencia de empuje y arrastre con respecto a la velocidad y ajustando esa igual a cero para determinar el máximo.
5.3.1 Caso cuando el empuje es constante
Un caso simple ocurre cuando se puede suponer que el empuje disponible de un motor es constante, una suposición que a menudo se hace para los motores a reacción. Si el empuje es constante la diferencia máxima entre empuje y arrastre y, por lo tanto, el ángulo máximo de ascenso, debe ocurrir cuando el arrastre es mínimo. Una vez más las condiciones mínimas de arrastre se convierten en las óptimas para un parámetro de rendimiento. También debería ser obvio que cuando el empuje no es una constante, el arrastre mínimo probablemente no sea la condición necesaria para el ángulo máximo de ascenso.
El lector debe señalar que en lo anterior no se ha hecho referencia alguna a una resistencia parabólica polar y las conclusiones alcanzadas no se limitan a tal caso. En el caso del polar de arrastre parabólico sabemos determinar los coeficientes de sustentación y arrastre y la velocidad para arrastre mínimo de nuestro estudio anterior.
A continuación se muestra una gráfica típica de potencia versus velocidad. Sabemos desde arriba que la tasa de ascenso es igual a la diferencia en la potencia disponible y la requerida, a una velocidad dada, dividida por el peso de la aeronave. Así, la gráfica de potencia disponible/ potencia requerida puede ser utilizada para determinar gráficamente la tasa de ascenso a cualquier velocidad de la misma manera que se utilizaron las curvas de empuje anteriores. En los casos en que la potencia disponible se asume constante, como suele ser el caso en una simple representación de una aeronave propulsada por hélice, la velocidad máxima de ascenso ocurrirá a la velocidad donde la potencia requerida es mínima. Sabemos del capítulo anterior cómo determinar las condiciones para la potencia mínima requerida. Si la potencia disponible no es constante, la velocidad máxima de ascenso no necesariamente ocurrirá a la velocidad para la potencia mínima requerida.
Obsérvese que la gráfica que se muestra a continuación traza P√σ versus Ve ya que esto permite que los datos de potencia requeridos en todas las altitudes colapsen a una sola curva como se deriva en el Capítulo 4.
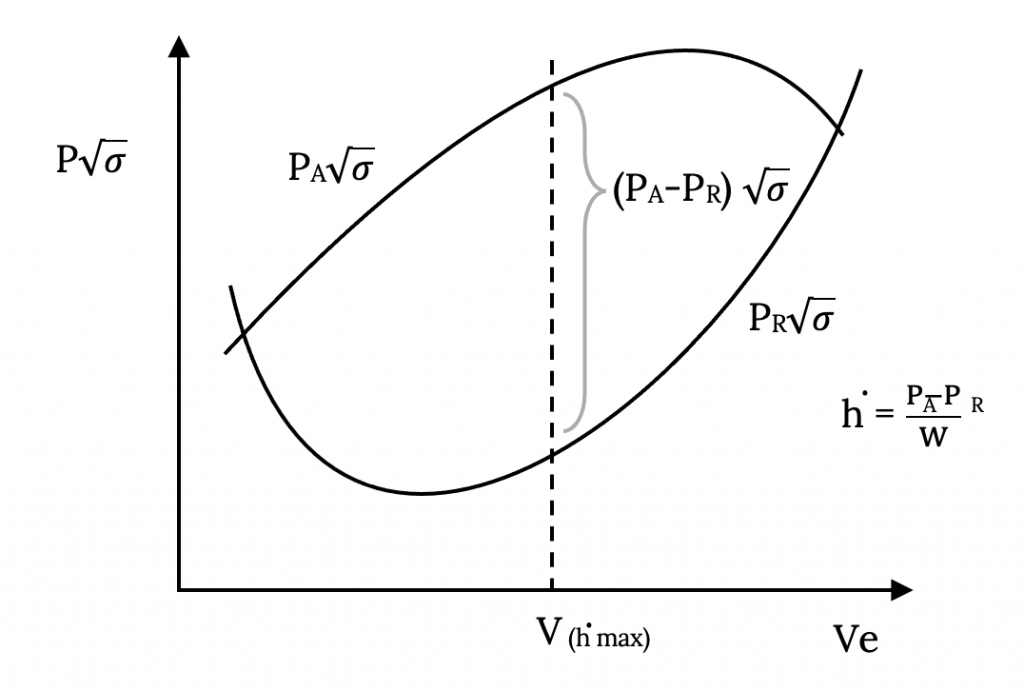
También hay que señalar que la tasa máxima de ascenso y el ángulo máximo de ascenso no ocurren a la misma velocidad.
Es interesante comparar las curvas de rendimiento de potencia, y de ahí la tasa de ascenso, para los dos modelos simples que hemos elegido para aviones jet y prop. En la trama que sigue, se supone que el avión de proa tiene potencia constante disponible y que el jet tiene empuje constante. Dado que la potencia disponible es igual al empuje multiplicado por la velocidad, los datos disponibles de potencia del chorro se encuentran en una línea diagonal que comienza en el origen. La curva de potencia requerida asume una aeronave común. En otras palabras, se trata de una comparación del mismo avión con dos tipos diferentes de motor. Es obvio que a velocidades más bajas la velocidad de ascenso para el puntal excede a la del jet mientras que a velocidades más altas el jet puede superar al puntal. Esta comparación, aunque ficticia, es típica de las diferencias entre aviones similares a reacción y propulsores. Muestra una razón por la que uno no diseñaría un plumero de cultivo propulsado por jet ya que un avión de este tipo necesita una alta tasa de ascenso a velocidades muy bajas.
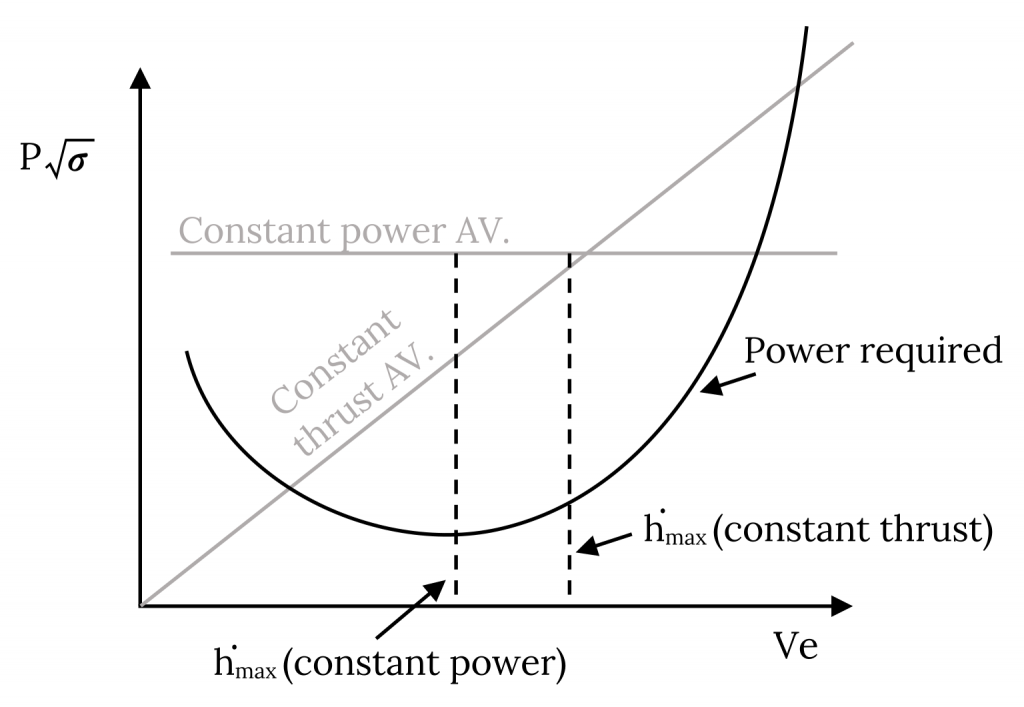
5.3.1.1 Caso Especial: Empuje Constante
En el caso mencionado anteriormente como modelo simple para un avión a reacción, encontrar el ángulo máximo de ascenso es fácil ya que debe ocurrir a la velocidad para arrastre mínimo o relación máxima elevación-arrastre. Las condiciones para la tasa máxima de ascenso no son tan simples. Mirando la tasa de ascenso nuevamente recordamos
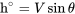
y suponiendo vuelo cuasi-nivel podemos escribir
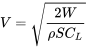
Así, tenemos una relación que tiene como variable el coeficiente de elevación.
De nuevo subiendo la suposición cuasi-nivel que asume que la elevación es esencialmente igual al peso
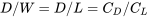
Ahora tenemos una relación que incluye tanto los coeficientes de elevación como los de arrastre como variables.
Sin embargo, sabemos que el coeficiente de arrastre depende del coeficiente de sustentación en el polar de arrastre.
Esto da
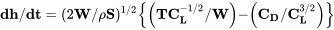
o
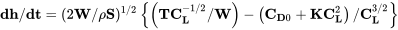
La ecuación anterior es para el caso de empuje constante y muestra la tasa de ascenso en función de una sola variable, el coeficiente de sustentación. Para determinar la tasa óptima de ascenso es necesario entonces tomar la derivada de esta ecuación con respecto al coeficiente de sustentación. Solo los términos entre paréntesis deben incluirse en la derivada ya que se establecerá igual a cero.
Esto da
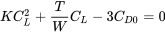
que se puede resolver a través de la ecuación cuadrática para encontrar el valor del coeficiente de sustentación que dará la mayor tasa de ascenso para este caso especial de empuje constante.
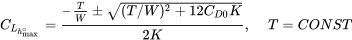
EJEMPLO 5.3
Una aeronave dada tiene C D0 =0.013, K = 0.157, W = 35.000 lb, S = 530 pies cuadrados, T/W = 0.429 y el empuje es constante con la velocidad. Encuentra la mejor tasa de ascenso y el ángulo de ascenso asociado.
Antes de comenzar nuestra solución debemos asegurarnos de entender lo que se pide. Tenga en cuenta que no se solicitó el mejor ángulo de ascenso. El ángulo de ascenso buscado fue el que para el mejor índice de ascenso caso. Los estudiantes a veces asumen que la respuesta buscada es siempre para algún caso óptimo.
Para encontrar la tasa máxima de ascenso utilizamos la relación encontrada anteriormente para resolver el coeficiente de elevación.
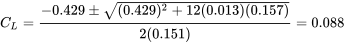
Esto luego se puede utilizar para encontrar la velocidad de vuelo asociada para la tasa máxima de ascenso.
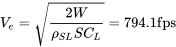
El ángulo de ascenso para la tasa máxima de ascenso (no el ángulo máximo de ascenso) se puede encontrar de la siguiente manera:
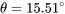
Por último, estos se utilizan juntos para encontrar la tasa de ascenso en sí.
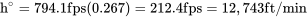
Nota: las unidades de pies por minuto son tradicionales.
Ahora veamos el otro óptimo, el de ángulo máximo de ascenso para este mismo avión. El ángulo máximo de ascenso ocurre en condiciones de arrastre mínimo o L/D máximo.
Entonces podemos encontrar el coeficiente de sustentación asociado con el ángulo máximo de ascenso y la velocidad aerodinámica a la que se produce.
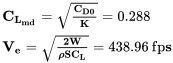
Por último, la tasa de ascenso para el ángulo máximo de ascenso
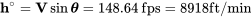
Echemos un vistazo a las respuestas anteriores y asegurémosle que son lógicas.
- La tasa máxima de ascenso debe ser mayor que la tasa de ascenso para el ángulo máximo de ascenso. ¿Eso es cierto?
- El ángulo de ascenso para la tasa máxima del caso de ascenso debe ser menor que el ángulo máximo de ascenso. ¿Eso es cierto?
- El ángulo máximo de ascenso debe ocurrir a una velocidad aérea menor que la de la velocidad máxima de ascenso. ¿Ese es el caso?
En todos los casos se satisfacen las preguntas anteriores. Estas son algunas de las preguntas que el alumno debe hacer al revisar las soluciones a un problema. A menudo, hacer preguntas como estas puede detectar errores que de otro modo podrían ignorarse.
Una situación en la que todos los pilotos están interesados tanto en la tasa de ascenso como en el ángulo de ascenso es en el despegue. En un despegue normal el piloto quiere subir inicialmente a la velocidad que dará la máxima tasa de ascenso. Esto permitirá que la aeronave gane altitud en el menor tiempo posible, un objetivo importante como precaución contra el motor u otros problemas en el despegue. Si un motor falla en el despegue, se desea una altitud máxima para permitir tiempo para recuperarse y realizar un aterrizaje de emergencia. Hay, sin embargo, algunas situaciones en las que lo mejor para el piloto es renunciar a la mejor tasa de ascenso e ir por el mejor ángulo de ascenso. Un caso obvio es cuando la aeronave debe despejar un obstáculo al final de la pista como un árbol o una torre. La siguiente figura ilustra ambos casos.
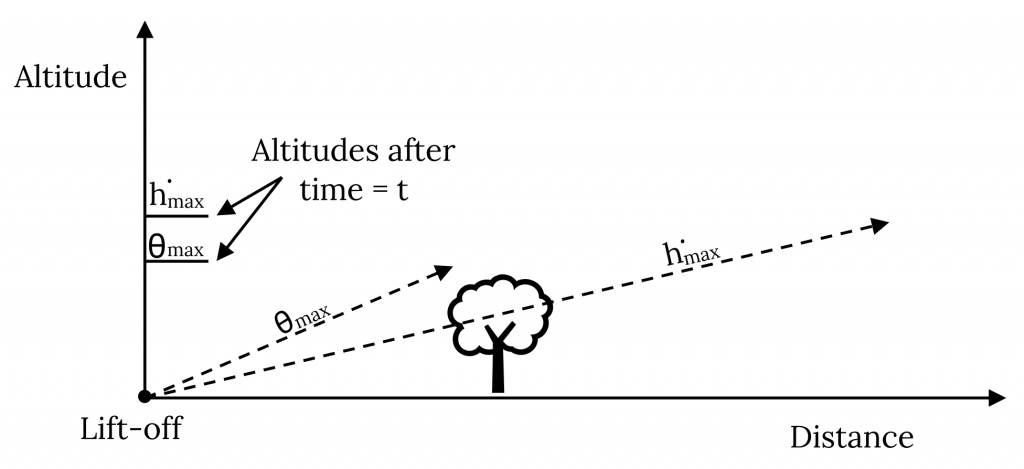
¡El avión que voló a la velocidad máxima de ascenso habría alcanzado la altitud deseada más rápido que el avión que voló con el máximo ángulo de ascenso si ese árbol no hubiera estado en el camino!
5.4 Tiempo de Subir
Para encontrar el tiempo para subir de una altitud a otra debemos integrar a lo largo del diferencial de tiempo
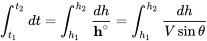
Para integrar esta expresión debemos saber cómo varía V sin θ en función de la altitud. Normalmente nos va a interesar el tiempo mínimo para escalar como caso limitante. Esto, por supuesto, ocurrirá a la velocidad para el máximo índice de ascenso. Esta velocidad será una función de la altitud.
Si podemos encontrar la tasa de ascenso en cada altitud podemos trazar tasa de ascenso versus altitud como se muestra a continuación. El área bajo la curva entre las dos altitudes deseadas representa el tiempo para escalar entre esas dos altitudes.
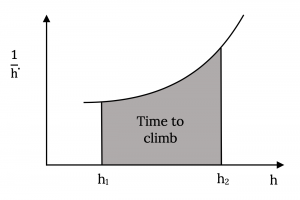
Cualquiera de los métodos anteriores se puede utilizar para encontrar el tiempo para escalar. En realidad son lo mismo. El método analítico puede no ser tan sencillo como parece al principio ya que las ecuaciones deben dar cuenta de la variación de velocidad y ángulo de ascenso con la altitud, requiriendo la incorporación de las ecuaciones de densidad de altitud estándar en la integral. Las ecuaciones podrían simplificarse asumiendo una subida de velocidad constante o una subida en ángulo constante.
5.5 Variación de potencia con altitud
Anteriormente abordamos la variación de la potencia requerida (para superar el arrastre) con la altitud y cómo las curvas de potencia requerida podrían fusionarse en una sola trazando la potencia multiplicada por la raíz cuadrada de la relación de densidad. La potencia disponible también debe multiplicarse por la raíz cuadrada de la relación de densidad para ser incluida en la misma parcela de rendimiento. Además de esto debemos ser conscientes de cómo la potencia disponible realmente varía con la altitud.
Tanto para los motores a reacción (turborreactor, fan-jet y turbohélice) como para los motores de pistón, la potencia producida por el motor disminuye en proporción a la disminución de la densidad con el aumento de la altitud.
![PAVρ, PALT=PSL [ρalt/ρSL]](https://eng.libretexts.org/@api/deki/files/49319/e606b34a97eb6ef3f3899302d2d3b062.png)
Para un motor de pistón turboalimentado, el turbocompresor está diseñado para mantener las condiciones de admisión del nivel del mar hasta cierta altitud de diseño. Un modelo simple de variación de potencia con altitud para un motor turboalimentado tendrá una potencia constante en su valor de nivel del mar hasta aproximadamente 20,000 pies y descendiendo en proporción directa a la disminución de la densidad a altitudes más altas.
![PAV= [CONST] SL20,000 PAV= [CONST] SL20,000](https://eng.libretexts.org/@api/deki/files/49320/5da550111b1018f4dd7ee93046b76f8f.png)
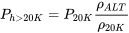 20k=P20KρAltρ20K” title=” pH>20k=P20KρAltρ20K” class=” mathml mathjax” >
20k=P20KρAltρ20K” title=” pH>20k=P20KρAltρ20K” class=” mathml mathjax” >
Situaciones más complicadas son posibles con múltiples etapas de turboalimentación.
Debe recordarse que al trazar datos de potencia versus la velocidad equivalente del nivel del mar debemos tener en cuenta la variación real de potencia disponible como se acaba de discutir y multiplicar ese resultado por la raíz cuadrada de la relación de densidad para hacer compatibles las curvas de potencia disponibles con las curvas de potencia requerida. Esto no es redundante. El primer cambio se realiza para tener en cuenta los efectos reales de altitud y el segundo para un esquema de trazado necesario para colapsar todos los datos de potencia requeridos en una sola curva.
5.6 Altitudes de techo
En discusión anterior hablamos de la altitud del techo como aquella en la que ya no era posible subir. Esta sería la altitud donde la curva de potencia disponible apenas toca la curva de potencia requerida, lo que indica que la aeronave puede volar recto y nivelar a una sola velocidad a esa altitud. Aquí la tasa máxima de ascenso es cero. Definimos esta altitud como el techo absoluto. Esta definición es, sin embargo, algo engañosa.
Teóricamente, basado en nuestro estudio anterior, tomaría una cantidad infinita de tiempo alcanzar la altitud del techo. Se podría observar la velocidad de ascenso posible para una aeronave que está, digamos, a 500 pies por debajo de su techo absoluto. Se encontraría una tasa de ascenso muy baja, resultando en una cantidad muy grande de tiempo requerido para subir que duran 500 pies para alcanzar el techo absoluto. Debido a esto definimos un techo más práctico llamado techo de servicio. La definición del techo de servicio se basa en la tasa de ascenso; es decir, a qué altitud es la tasa máxima de ascenso tan baja que hace poco práctico seguir subiendo. Esto es diferente para aviones impulsados por jet y pistón. Para la aeronave de pistón, el techo de servicio es la altitud a la que la velocidad de ascenso es de 100 pies por minuto (o 0.5 metros por segundo). Para los aviones a reacción, el techo de servicio es la altitud a la que la velocidad de ascenso es de 500 pies por minuto (o 2.5 metros por segundo).
Cabe señalar que muchos aviones de combate y de alto rendimiento pueden, en realidad, ser capaces de superar incluso su techo absoluto mediante el uso de enfoques de gestión energética. Un avión puede subir a su techo de servicio, por ejemplo, y luego entrar en una inmersión, acumulando el exceso de energía cinética, para luego reanudar una escalada, utilizando tanto el exceso de potencia como el exceso de energía cinética para subir a altitudes más altas que las encontradas como “absolutas”. Además, a muy gran altitud puede ser necesario incluir dinámicas orbitales en la consideración de capacidades de ascenso y techo.
Testo 5
1. Un avión pesa 3000 lb y tiene un área de ala de 175 pies 2, una relación de aspecto de 7 y un factor de eficiencia de Oswald, e, de 0.95. Si C D0 es 0.028, traza arrastre versus velocidad para el nivel del mar y altitudes de 10,000 pies, trazando arrastre en intervalos de 20 fps. También calcule los valores de arrastre mínimo y la velocidad para arrastre mínimo en ambas altitudes y compárelos con los resultados en su gráfica. Utilice el papel cuadriculado proporcionado; no trazar por computadora.
2. Usando un valor de empuje del nivel del mar de 400 lb y asumiendo que el empuje es constante con la velocidad pero varía con la densidad (altitud), calcule las velocidades máximas y mínimas reales del aire a nivel del mar y a altitudes de 10,000 pies y confirme estas respuestas gráficamente.
Referencias
Figura 5.1: Gris Kindred (2021). “Fuerzas en Subida”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/5.1_20210805
Figura 5.2: Gris Kindred (2021). “Relación Angular Velocidad/Tasa de Subida”. CC BY 4.0. Plano de Bayu Ardhy del Proyecto Noun. Dominio público. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/5.2_20210805
Figura 5.3: Gris Kindred (2021). “Alcance en un Deslizamiento”. CC BY 4.0. Plano de Bayu Ardhy del Proyecto Noun. Dominio público. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/5.3_20210805
Figura 5.4: James F. Marchman (2004). “Descomposición de Coeficientes de Elevación y Arrastre” CC BY 4.0.
Figura 5.5: Gris Kindred (2021). “Influencia de Empuje y Arrastre al Subir CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/5.5-new
Figura 5.6: Gris Kindred (2021). “Capacidad de Subida en Gráficas de Potencia”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/5.6-new
Figura 5.7: Gris Kindred (2021). “Comparación de Cajas Disponibles de Potencia Constante y Empuje Constante”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/5.7_20210805
Figura 5.8: Gris Kindred (2021). “Subir a Maxima en el despegue”. CC BY 4.0. Árbol de Richard del Proyecto Noun. Dominio público. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/5.8_20210805
Figura 5.9: Gris Kindred (2021). “Integrándose para conseguir tiempo para escalar”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/5.9_20210805
Figura 5.10: Gris Kindred (2021). “Parcela de Arrastre vs Velocidad y Empuje Disponible”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/hw-5_20210805
<! — pb_fixme —><! — pb_fixme —>


