8: Rendimiento Acelerado - Giros

Última actualización
Guardar como PDF

Page ID: 80892

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Introducción

Introducción Histórica

Hasta el momento, todo nuestro estudio de desempeño ha involucrado vuelo en línea recta. Desafortunadamente, a menos que nuestro avión esté volando desde una pista que esté exactamente en línea con nuestra pista de destino y no haya viento en la ruta, ¡el vuelo en línea recta no es muy práctico! Tenemos que ser capaces de girar.

Si bien la necesidad de poder girar es bastante obvia para nosotros, una mirada a la aviación temprana mostrará que a menudo era lo último en la mente de muchos pioneros de la aviación. La singularidad del Wright Flyer no era su capacidad para volar unos metros en línea recta sobre la arena en Kitty Hawk. Fue único en su capacidad de girar y maniobrar. Hay afirmaciones de que experimentadores anteriores en Inglaterra, Francia, Rusia y Estados Unidos pueden haber hecho “lúpulos” cortos e incontrolados o incluso “vuelos” legítimos en línea recta en vehículos motorizados antes del 17 de diciembre de 1903 pero no hay reclamos de vuelo “controlado” de un motor, más pesado que el aire, hombre (o mujer) transportando vehículo con anterioridad a esta fecha.

Hay varias formas de girar un vehículo en vuelo. Los primeros experimentadores como Otto Lilienthal en Alemania y Octave Chanute en este país sabían que cambiar el peso del “piloto” suspendido debajo de sus primeros “ala delta” se inclinaría o “depositaría las alas para permitir giros. Otros como Samuel P. Langley, director de principios de siglo del Smithsonian que contaba con fondos del gobierno para construir y volar el primer avión, diseñaron su embarcación para ser dirigida con un timón como un barco. Ninguno de los dos métodos de torneado fue muy eficiente. Langley es más pesado que los modelos con propulsión aérea, por ejemplo, voló muy bien pero no pudo adaptarse a los vientos y voló en círculos largos en lugar de una línea recta como habían sido diseñados para hacer.

Al depositar las alas (llamados “aviones” en la década de 1890) se inclina la fuerza de sustentación hacia un lado y el componente lateral de la elevación da como resultado un giro, pero dado que parte del elevador se está utilizando ahora para girar el vehículo, la elevación restante puede no ser suficiente para oponerse al peso a menos que se agregue potencia adicional. El uso de un timón solo resulta en una fuerza lateral en el fuselaje de la aeronave y, por lo tanto, una fuerza de giro. El giro resultante, al hacer que un ala avance más rápido que el otro, suele conducir a un banco. Ninguno de los dos métodos, empleado solo, proporciona un medio de giro muy satisfactorio y el resultado suele ser un giro de radio muy grande. Muchos experimentadores tempranos, de hecho, parecían querer girar sin banca ya que estaban “volando” muy cerca del suelo y un ala bancada podría tocar el suelo y provocar un choque.

Los hermanos Wright diseñaron un mecanismo complejo que involucra timones coordinados y torsión de alas para combinar tanto el balanceo como la guiñada en un giro “coordinado” y eficiente. Su propósito original pudo haber sido en realidad tratar de depositar el avión frente al giro para evitar el contacto con el suelo por el ala pero encontraron que un giro debidamente coordinado podría hacer que su vehículo fuera bastante maniobrable. Cuando los Wright llevaron sus aviones a Europa en 1908 sorprendieron a los aviadores europeos con la capacidad de su nave para girar y maniobrar. Los aviones franceses, que eran los más sofisticados de Europa, utilizaban únicamente timones para girar. El Wright Flyer, con su sistema de “deformación de alas” y timón coordinado, fue literalmente capaz de volar círculos alrededor de la aeronave francesa.

Los Wright habían hecho este sistema de cuerdas y poleas que conectaban el timón con las puntas retorcidas de las alas a una cuna debajo del cuerpo del piloto, el foco central de su patente en el avión. Cuando el poseedor del récord mundial de motocicletas de alta velocidad y diseñador de motores Glenn Curtiss, con fondos de Alexander Graham Bell y otros, construyó y voló un avión con un rendimiento tan bueno o mejor que el Wright Flyer, los Wrights demandaron por violación de patente. Los aviones Curtiss, que utilizaban alas pequeñas y separadas cerca de las puntas de las alas o aletas triangulares montadas en la punta del ala (que luego se llamarían alerones) y que se basaban en la operación piloto de controles separados como el sistema de bastón y timón de hoy, lograron el mismo rendimiento de giro que el Wrights Flyer. Curtiss, una figura mucho más extravagante y pública que cualquiera de los Wrights, rápidamente captó la atención y la imaginación del público estadounidense, enfureciendo a los Wrights que habían evitado la atención pública al tiempo que se convencían de que nadie más era capaz de duplicar sus hazañas aéreas.

La batalla judicial de una década entre Curtiss y la familia Wright por los derechos de patente de dispositivos capaces de convertir eficientemente un avión es acreditada por la mayoría de los historiadores como permitiendo a los aviadores y diseñadores europeos avanzar mucho por delante de los estadounidenses. Los Wrights estaban tan absortos en proteger su patente que no hicieron más esfuerzos para mejorar el avión y la amenaza de una demanda de Wright mantuvo fuera del negocio a todos los diseñadores de aviones estadounidenses, excepto Curtiss. Curtiss, cuya falta de respeto a la cautela le había permitido antes establecer el récord mundial de velocidad motorizada en una motocicleta con motor V‑8, con el apoyo moral y financiero de Bell y Henry Ford y otros, mantuvo la demanda de patente en los tribunales a través de apelación tras apelación y continuó construyendo y vendiendo aviones. Para sortear la patente de Wright, Curtiss, en un momento construyó su avión sin alerones ni otros controles de balanceo y luego los envió a la cercana Canadá donde una de las compañías de Bell agregó los alerones antes de que los aviones fueran enviados a clientes en Europa. En tanto, Curtiss siguió experimentando e innovando y no es casualidad que cuando la primera guerra mundial atrajo la participación estadounidense fuera Curtiss y no los aviones Wright los que iban a la guerra. Después de la guerra fue la famosa Curtiss “Jenny” la que trajo la era “barnstorming” de la aviación a todo Estados Unidos.

Espero que el lector perdure lo anterior deslizarse hacia la fascinación histórica. A estas alturas algunos de ustedes se preguntan ¿qué demonios tiene que ver todo esto con el rendimiento de los aviones por turnos? Los hechos son, sin embargo, que los primeros diez a quince años de vuelo estadounidense realmente estuvieron dominados por la capacidad de giro del avión.

8.1 La mecánica de un giro

Para mantener la física de nuestra discusión lo más simple posible, consideremos solo giros en radio constante en un plano horizontal. Este es el giro ideal sin pérdida o ganancia de altitud que cada estudiante piloto practica volando en círculos alrededor del silo de algún agricultor u otro hito prominente.

Nuestros objetivos al analizar el rendimiento de giro serán encontrar cosas como la velocidad máxima de giro y el radio de giro mínimo y determinar la potencia o empuje necesarios para mantener dichos giros. Comenzaremos por mirar dos tipos de giros.

Los aviones actuales, en general, hacen giros utilizando las mismas técnicas pioneras en los Wright y mejoradas por Curtiss; giros coordinados utilizando controles de timón y alerón para combinar balanceo y guiñada. ¡La principal excepción se encontraría en algunas maniobras evasivas de giro realizadas por aviones militares y en los giros cotidianos de la mayoría de los pilotos estudiantiles!

Los vehículos sin alas como misiles, dirigibles y submarinos siguen girando como los de los primeros aviadores franceses y del “Aeródromo” de Langleys, utilizando el timón y la fuerza lateral del cuerpo o fuselaje para generar un giro de “esquiar”. Examinaremos esta técnica antes de mirar el giro coordinado más sofisticado.

La aceleración en cualquier giro de radio$R$ viene dada por la siguiente relación:

\[a_r = \dfrac{V^2}{R}. \nonumber\]

Esta aceleración se dirige radialmente hacia adentro hacia el centro del círculo y se denomina correctamente la aceleración centripital.

También podemos considerar la aceleración desde la perspectiva de la tasa de cambio del “ángulo de rumbo”, ψ, como se muestra en la siguiente figura.

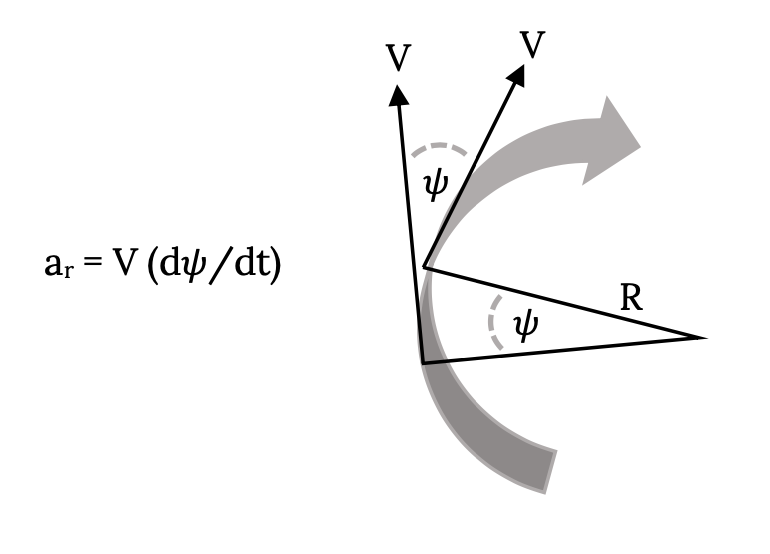
Para una aeronave en un giro constante, el ángulo a través del cual ha girado la aeronave se denota como el ángulo de rumbo psi. Psi forma el ángulo entre el vector de velocidad original y el ecurrent uno, ambos denotados como cap V. Un giro constante también indica que la aeronave es un radio constante cap R lejos del centro de curvatura. aceleración centripital a sub r es igual a cap V veces la velocidad de cambio del ángulo de rumbo, d psi sobre d t. — Figura 8.1: Ángulo de giro

La técnica de “deslizamiento para girar” se ilustra a continuación para un radio constante, giro horizontal. Se utiliza un timón (o incluso un empuje vectorizado) para inclinar el vehículo y la fuerza lateral creada por el flujo sobre la carrocería guiñada crea la aceleración deseada.

A) La aeronave tiene un límite de velocidad hacia adelante V y experimenta un límite de fuerza normal hacia adentro Y desde el giro en sentido horario. B) La aeronave ve fuerzas verticales opuestas desde la tapa de elevación L y la tapa de peso W, pero una tapa de fuerza lateral sin oposición Y. — Figura 8.2: “Deslizamiento para Girar” Usando Fuerza Lateral

Las ecuaciones del movimiento se convierten en

L — W = 0

Y = mV (d ψ /dt) = m (V ² /R)

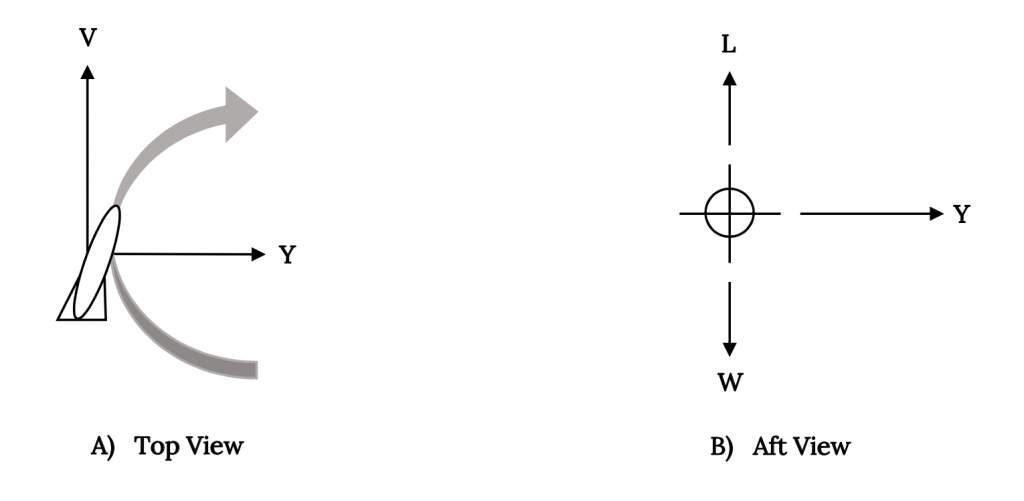
Para el giro del patín examinado anteriormente, la velocidad de giro y el radio dependen de la cantidad de fuerza lateral que se pueda generar en la carrocería del vehículo. Tenga en cuenta que el levantamiento (o flotabilidad en los casos de submarinos y dirigibles) no entra en el problema.

R = (WV ²)/(gY), d ψ /dt = (gY)/(WV)

Con las relaciones anteriores se puede determinar el radio y la velocidad para un giro horizontal donde la fuerza de la carrocería, no el levantamiento del ala, transporta el vehículo a través de un giro. Así giran los cohetes y misiles no alados. Los aviones utilizan una fuerza mucho más poderosa, la elevación, para girar. Al usar el elevador para proporcionar la fuerza lateral necesaria y para contrarrestar el peso de manera coordinada, un avión puede hacer un giro mucho más eficiente que los misiles o dirigibles.

Veamos el giro coordinado. En el giro coordinado ideal como se ilustra en la Figura 8.3, se utiliza la sustentación aerodinámica para equilibrar el peso de manera que se mantenga el vuelo horizontal y para proporcionar una fuerza lateral que produzca la aceleración de giro deseada. No se genera ninguna fuerza lateral real en el fuselaje de la aeronave. Este tipo de giro requiere que el piloto utilice el timón y los alerones y el acelerador para dar el equilibrio ideal de ángulo de inclinación y fuerzas lo que creará un giro de radio constante y mantendrá la altitud.

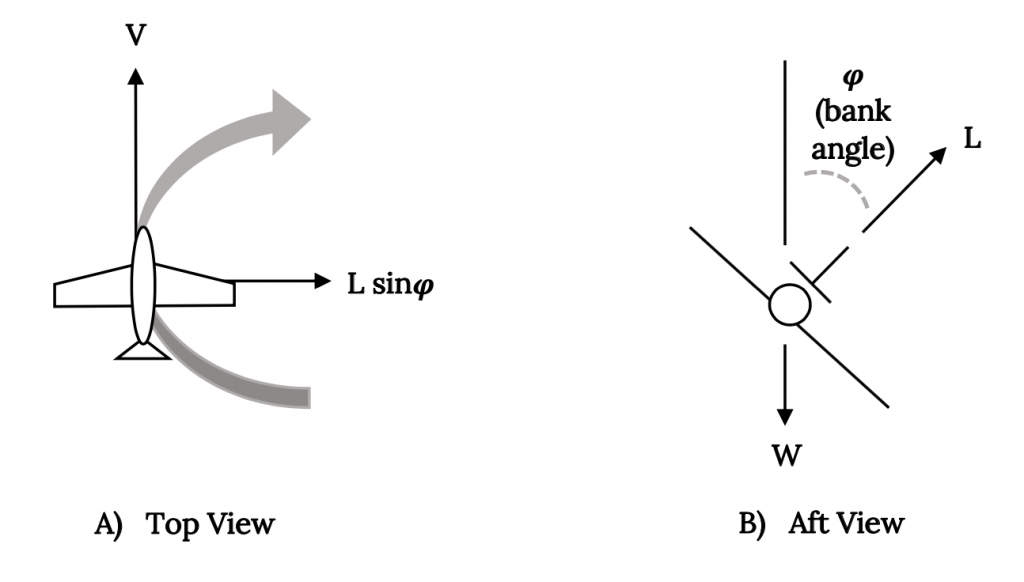
A) La aeronave ve fuerzas verticales opuestas desde la tapa de elevación L y la tapa de peso W, pero una tapa de fuerza lateral sin oposición Y. B) La aeronave está bancada de tal manera que el ala derecha es más baja que el ala izquierda. La aeronave experimenta una tapa de fuerza vertical descendente W por su peso, mientras que la tapa de fuerza de elevación L está inclinada a la derecha de la vertical por el ángulo de inclinación phi. — Figura 8.3: Giro Coordinado. Izquierda: Vista superior. Derecha: Vista en popa.

Si este giro se coordina adecuadamente, la aceleración combinada resultante y la fuerza gravitacional sentida tanto por el avión como por el piloto se dirigirán “hacia abajo” a lo largo del eje vertical de la aeronave y serán sentidas por el piloto como una fuerza incrementada en el asiento. El mal coordinado se sentirá como que incluye una fuerza lateral que empuja al piloto a la izquierda o derecha en el asiento. Estas mismas fuerzas actúan sobre la “bola” en el indicador de “vuelto-deslizamiento” de la aeronave, moviendo la pelota fuera del centro en un giro descoordinado. Veremos el indicador de vuelta-deslizamiento más adelante.

Si no se coordina un giro pueden ocurrir varios resultados. El radio de giro no será constante y el avión se “deslizará” hacia afuera a un giro de radio mayor o “deslizará” hacia adentro a un radio más pequeño. También podría haber una ganancia o pérdida de altitud.

En el giro coordinado, parte de la elevación producida por el ala se utiliza para crear la aceleración de giro. El resto del elevador aún debe contrarrestar el peso para mantener el vuelo horizontal.

Ahora nos encontramos buscando por primera vez en una situación en la que levantar no es igual a peso. En un giro coordinado el levantamiento debe ser mayor que el peso y definimos un “factor de carga”, n, para dar cuenta de esta desigualdad.

\[L = nW\]

Este factor de carga puede relacionarse entonces con el ángulo de inclinación utilizado en el giro, con el radio de giro y con la velocidad de giro. Volviendo a la ecuación de equilibrio de fuerzas vertical tenemos

\[\mathbf{L} \cos \varphi-\mathbf{W}=\mathbf{n} \mathbf{W} \cos \varphi-\mathbf{W}=\mathbf{0}\]

que da:

\[\cos \varphi=1 / \mathrm{n}\]

Usando la otra ecuación de movimiento podemos encontrar el radio de giro

\[\mathbf{R}=\left(\mathbf{m} \mathbf{V}^{2}\right) /(\mathbf{L} \sin \varphi)=\left(\mathbf{m} \mathbf{V}^{2}\right) /(\mathbf{n} \mathbf{W} \sin \varphi)=\left(\mathbf{V}^{2} / \mathbf{n g}\right)(\mathbf{1} / \sin \varphi)\]

Sabiendo que el coseno del ángulo de inclinación es igual a 1/n podemos encontrar el valor del seno del ángulo de inclinación mediante la construcción de un triángulo rectángulo

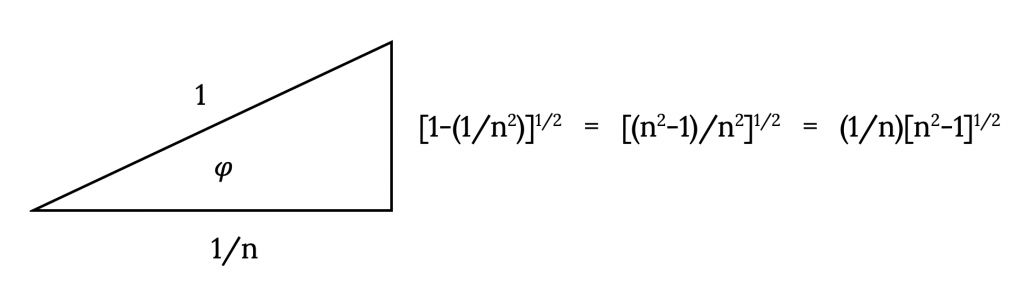
Un triángulo rectángulo con hipoteneo longitud 1 y ángulo agudo phi, tiene un lado adyacente de longitud 1 sobre n, y una longitud de lado opuesto de raíz cuadrada 1 menos 1 sobre n cuadrado, que es igual a la raíz cuadrada de n al cuadrado menos 1 en todo n cuadrado, que también es igual a 1 sobre n veces la raíz cuadrada de n al cuadrado menos 1. — Figura 8.4: Relación trigonométrica entre el ángulo de giro phi y el factor de carga n

por lo tanto,

$sinφ= [(n2−1) /n2] 1/2andtanφ= [n2−1] 1/2$

y el radio de giro se convierte en

R = (V ²/g) {1/[n ² — 1] ^1/2}.

Al tratar con los giros debemos recordar que el levantamiento ya no es igual al peso. El coeficiente de elevación es entonces

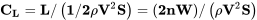
$CL=L/ (1/2ρV2S) = (2nW)/(ρV2S)$

por lo tanto

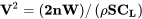
$V2= (2nW)/(ρSCl)$

Lo anterior nos permite escribir el radio de giro de otra manera,

$R= [2W/ (ρGSCl)] [n/ (n2−1) 1/2]$

Cabe señalar aquí que si se desea un radio de giro pequeño se necesita un alto factor de carga y coeficiente de sustentación y baja altitud ayudará. La carga de ala alta (W/S) también permitirá un giro más apretado.

La tasa de giro en un giro coordinado es

$dψ/dt= (Lsinφ)/(mV) = {(nmg)/(mV)} sinφ= [ng/V] [(n2−1) 1/2/n]$

$dψ/dt= (g/V) [n2−1] 1/2$

Alternativamente,

$dψ/dt=g {[(ρSCL)/(2W)] 1/2 [(n2−1) /n] 1/2}$

Los mismos factores que contribuyen a pequeños radios de giro dan altas tasas de giro.

8.2 Factor de carga (n)

De las ecuaciones anteriores es obvio que el factor de carga juega un papel importante en los giros. En vuelo recto y nivelado el factor de carga, n, es 1. En maniobras de cualquier tipo el factor de carga será diferente a 1. En un giro como los descritos es obvio que n superará 1. Lo mismo ocurre en maniobras como los “pull ups”.

El factor de carga es simplemente una función de la cantidad de sustentación necesaria para realizar una maniobra dada. Si el ángulo de inclinación requerido para un giro coordinado es de 60°, el factor de carga debe ser igual a 2. Esto significa que la elevación es igual al doble del peso de la aeronave y que la estructura de la aeronave debe ser suficiente para llevar esa carga. También significa que el piloto y los pasajeros deben ser capaces de tolerar la carga que les impone este giro, carga que está forzando su cuerpo a entrar en su asiento con un efecto doble que el de la gravedad normal. Esta carga o aceleración “2g” también está forzando su sangre de la cabeza a los pies y teniendo otros efectos interesantes en el cuerpo humano.

Si nos fijamos en la relación de elevación

L = n _max W = C _Lmax [½ ρ V ² S]

vemos que la elevación máxima y por lo tanto el factor de carga máxima que puede generarse aerodinámicamente es una función del coeficiente de sustentación máxima (condiciones de calado).

Uno debe darse cuenta de que la aeronave, o, más precisamente, sus alas, pueden ser capaces de generar factores de carga mucho más altos que los que el piloto y los pasajeros o la estructura de la aeronave pueden tolerar. No es difícil diseñar aviones que puedan tolerar “cargas g” mucho más altas que el cuerpo humano, incluso cuando el cuerpo está en posición boca abajo en un asiento especialmente diseñado y uniforme. ¡Los ingenieros de la industria te dirán que podrían diseñar cazas mucho más ágiles a un costo mucho menor si los militares no insistían en tener pilotos en la cabina!

Todos los aviones, desde un Cessna 152 hasta el X‑31, están diseñados para tolerar ciertos factores de carga. La versión aeróbica del Cessna 152 está certificada para tolerar un factor de carga mayor que la versión “de cercanías” de esa aeronave. Una aeronave acrobática debe diseñarse para un factor de carga de 6.

La FAA también impone ciertas restricciones de vuelo a las aeronaves comerciales basadas en la comodidad de los pasajeros. Es posible hacer acrobacias aéreas en un Boeing 777 pero a la mayoría de los pasajeros no les gustaría. Por lo tanto, los pasajeros que transportan vuelos comerciales normalmente se restringen a “cargas g” de 1.5 o menos a pesar de que los propios aviones son capaces de mucho más.

8.3 El giro de dos minutos

Los pilotos de aviación general suelen estar familiarizados con el giro de “tarifa estándar” o de “dos minutos”. Este giro, a una velocidad de tres grados por segundo (0.05236 rad/s), se utiliza en maniobras bajo condiciones de vuelo instrumentales controladas. Para hacer tal giro, el piloto utiliza un instrumento llamado indicador de “vuelta-deslizamiento”. Este instrumento, ilustrado a continuación, consiste en un giroscopio que está parcialmente sujeto y unido a un indicador de aguja, y un tubo curvo que contiene una bola de queroseno blanco. A medida que el avión gira, el giroscopio desvía la aguja indicadora a medida que intenta permanecer fija en la orientación. La fuerza de “precesión” del giroscopio y el desplazamiento de la aguja resultante es proporcional a la velocidad de giro. La precisión de esta indicación no depende del grado en que se coordine el giro. El balón en el tubo curvo permanecerá centrado si el giro está coordinado mientras se moverá hacia un lado (derecha o izquierda) si no está coordinado. Uno de los juegos de marcas en la cara del instrumento indica un giro de dos minutos.

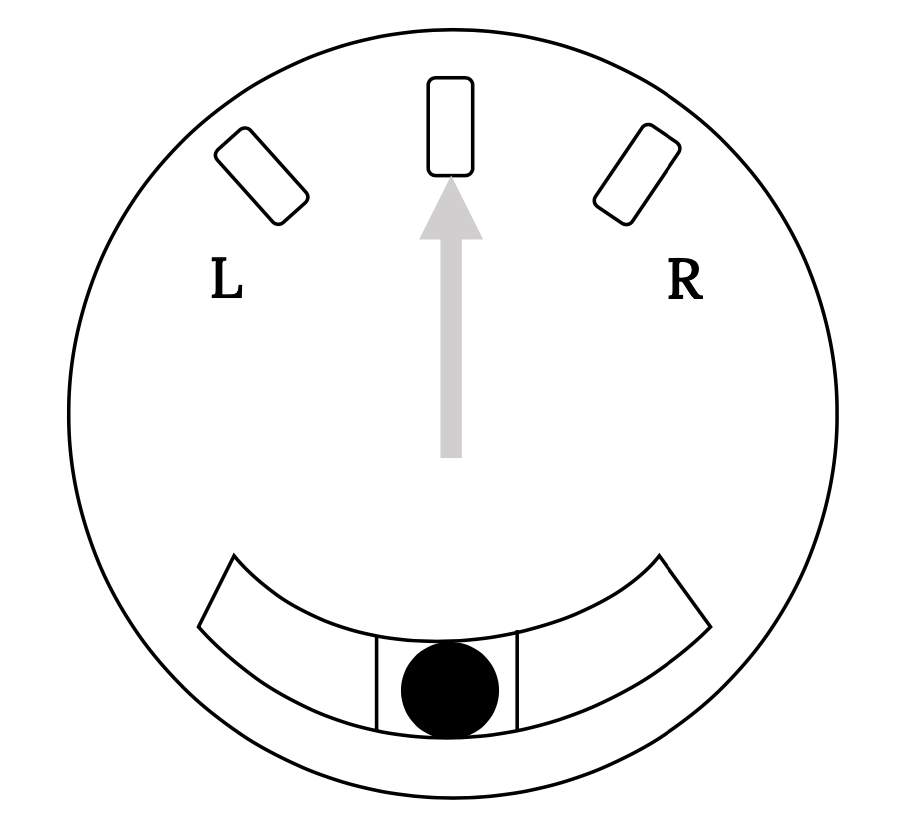
Se muestra un indicador que se asemeja a un indicador de combustible del vehículo. Una flecha apunta hacia arriba a una marca hash en el centro del borde superior, con dos marcas hash aproximadamente 30 grados a la izquierda y derecha de la marca hash central, etiquetadas cap L y cap R, respectivamente. En la parte inferior del calibre hay un canal con una bola negra en el centro. Dos líneas verticales marcan un área ligeramente más ancha que el diámetro de la bola en el centro del canal. — Figura 8.5: Indicador de vuelta-deslizamiento

8.4 El indicador de vuelta-deslizamiento

Para hacer un giro de dos minutos, el piloto solo necesita colocar la aeronave en un giro de tal manera que la aguja esté en la indicación de giro estándar en la dirección deseada. Para girar 90º se mantiene la velocidad de giro durante 30 segundos, un minuto para 180º, etc. Se utiliza el indicador de velocidad vertical (tasa de ascenso) para mantener la altitud y la pelota se mantiene centrada para coordinar el giro.

A muchos pilotos se les enseña, incorrectamente, que la marca de giro de dos minutos en el indicador de vuelta-deslizamiento es una indicación de un ángulo de inclinación de 15 grados, siendo la siguiente marca de 30º y así sucesivamente. Algunos pilotos incluso se refieren al indicador de giro deslizante como el indicador de “giro bancario” cuando el instrumento no tiene absolutamente ninguna manera de detectar el banco. Es posible, utilizando una técnica de “control cruzado”, girar la aeronave vía guiñada sin bancada (al igual que un misil gira) y ver que el instrumento indica la velocidad correcta de giro a pesar de que no hay banco y, de igual manera, la aeronave puede colocarse en rollo sin girar y el indicador permanecerá centrado.

¿Por qué ocurriría este error en la instrucción de vuelo? La respuesta radica en parte en la dificultad de erradicar la tradición de larga data y en parte en el hecho de que, para un avión pequeño entrenador de aviación general, se produce un giro coordinado de dos minutos en un ángulo de inclinación de aproximadamente 15 grados. Veamos los números.

De nuestras ecuaciones anteriores tenemos

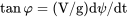
$tanφ= (V/g) dψ/dt$

Al insertar quince grados como ángulo de inclinación y una velocidad de giro de dos minutos (0.05236 rad/s), se obtiene una velocidad de 165 pies/seg o 112 mph. Esto, en efecto, se acerca a la velocidad a la que un avión de este tipo volaría en un giro. Sin embargo, si miramos un avión más rápido, digamos uno que opera a 350 millas por hora, y usamos la velocidad de giro de dos minutos, ¡obtenemos un ángulo de inclinación muy diferente de 30 grados!

Supongamos que usted es un pasajero en un Boeing 737 viajando a 600 mph y el piloto configuró un giro de dos minutos. Esto daría un ángulo de inclinación de 55 grados. ¡También daría un factor de carga de 1.75! Esto es más alto de lo que permite la FAA para las operaciones de las aerolíneas. Por esta razón, los aviones utilizan tasas de giro más lentas que el giro de dos minutos en vuelo y solo hacen giros de dos minutos a bajas velocidades, tal vez cuando operan en el “patrón” alrededor de los aeropuertos.

8.5 Condiciones de giro instantáneas versus sostenidas

Las relaciones previamente derivadas darán la velocidad de giro instantánea y el radio para un conjunto dado de condiciones de vuelo. En otras palabras, para un determinado conjunto de condiciones iniciales de vuelo podemos determinar la velocidad de giro y el radio, etc. Otra pregunta que debe hacerse es “¿Puede el avión sostener esa velocidad de giro?” El piloto puede ser capaz de, por ejemplo, colocar el avión en un banco de 60 grados a 250 mph pero puede encontrar que no hay suficiente empuje del motor para mantener esa velocidad y ángulo de inclinación mientras mantiene la altitud.

Ejemplo$\PageIndex{1}$

Para el avión con las especificaciones a continuación encontrará la velocidad máxima de giro y el radio mínimo de giro y las velocidades a las que ocurren. Determinar también si este giro puede sostenerse en condiciones estándar a nivel del mar.

W/S = 59.88 lb/ft ²

S = 167 ft ²

C _Lmáx = 1.5

n _máx = 6

C _D0 = 0.018

K = 0.064

T _max = 5000 lb

La velocidad máxima de giro es

$dψ/dt=g {[(ρSCLmax)/(2W)] 1/2 [(nmax2−1) /nmax] 1/2$

= 0.424 rad/seg = 24.29 ^o/seg.

La velocidad para esta velocidad de giro es

$V= [(2nW)/(ρSCLmax)] 1/2=448.6pies/seg$

El radio de giro mínimo es

$Rmin= [2W/ (ρgSCLmax)] [n/ (n2−1) 1/2] =1058ft=v/ [dψ/dt]$

Ahora debemos ver si el avión tiene el empuje suficiente para operar en estas condiciones. El coeficiente de arrastre en el coeficiente de sustentación máximo es

C _D = 0.018 + 0.064 C _Lmax ² = 0.162.

A la velocidad que se encuentra por encima del arrastre es entonces

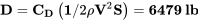
$D=CD (1/2ρV2S) =6479lb$

¡Este arrastre supera el empuje disponible del motor de la aeronave!

Si la aeronave anterior entra en un giro coordinado a la velocidad máxima de giro, rápidamente disminuirá a una velocidad más baja y una velocidad de giro con un radio de giro más grande o perderá altitud.

8.6 El diagrama V‑n o V‑g

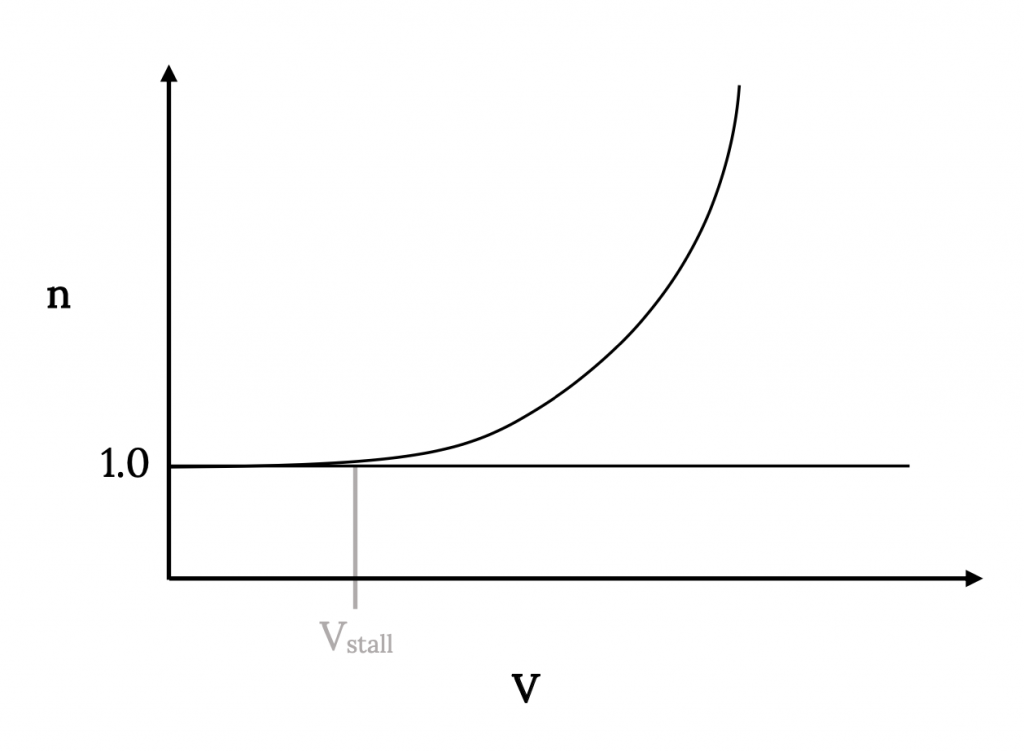
Una gráfica que a veces se utiliza para examinar la combinación de limitaciones estructurales y aerodinámicas de la aeronave relacionadas con el factor de carga es el diagrama V‑n o V‑g. Esta es una gráfica del factor de carga n versus velocidad.

Sabemos que cuando el levantamiento supera el peso

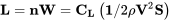
$L=Nw=CL (1/2ρV2S)$

Sabemos que un límite se impone por el puesto

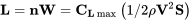
$L=NW=CLmax (1/2ρV2S)$

Reordenando esto podemos escribir

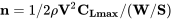
$N=1/2ρV2CLmax/ (W/S)$

y podemos reorganizar esto como

$V= [2nW/ (ρSCLmax)] 1/2$

Trazar n versus V dará entonces una curva como la que se muestra a continuación.

El factor de carga n en el eje vertical y el límite de velocidad V en el eje horizontal se utilizan para trazar una porción del régimen de carga para una aeronave. Para factores de carga inferiores a 1, la subcalada de la tapa V es una línea vertical constante. Después de n igual a 1, el pico V sub calado aumenta, dando como resultado una curva parabólica para n como una función de la sub calada de la tapa V. — Figura 8.6: Porción de calado de un diagrama V-n (solo alfa positivo)

También podemos considerar factores de carga negativos que se relacionarán con la pérdida “invertida”; es decir, la parada en ángulo de ataque negativo. En ángulo de ataque negativo, a menos que el ala esté desenrollada y construida con secciones simétricas de superficie aerodinámica, CL _max será diferente de la que tiene un ángulo de ataque positivo. Esto dará una curva diferente pero similar por debajo del eje. Combinando esto con la trama anterior da la siguiente trama.

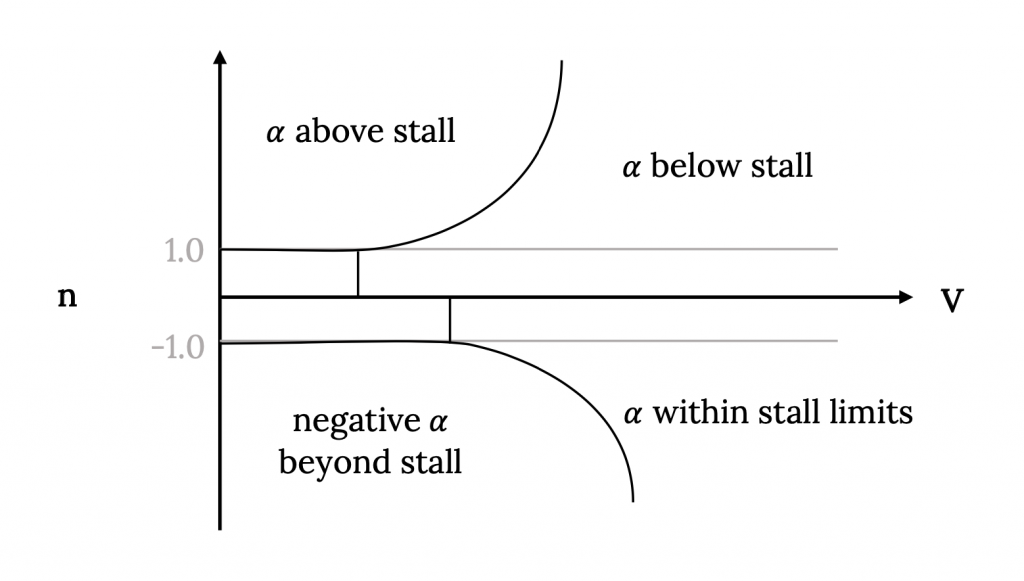
Se expande la misma gráfica que antes, con una versión espejada que ahora se muestra debajo del eje V de tapa horizontal para factores de carga negativos. La curva negativa está desplazada horizontalmente de la curva positiva original, comenzando en un valor de subcalado superior de la tapa V. La región a la izquierda de ambas curvas se denota como las regiones para alfa por encima del calado por encima del eje horizontal, y alfa negativa más allá de la calada por debajo del eje horizontal. A la derecha de cada curva, alfa está por debajo de la calada para factores de carga positivos, o alfa está dentro de los límites de calado para factores de carga negativos. — Figura 8.7: Porción de calada completa del diagrama V-n

A la izquierda de esta curva se encuentra la región de vuelo posterior a la parada que, con la excepción de los aviones militares de alto rendimiento, representa un área fuera de los límites de vuelo.

También se deben considerar otros límites. Obviamente habrá un límite de velocidad superior como el que se encontró anteriormente para vuelos rectos y nivelados. También habrá límites impuestos por el diseño estructural de la aeronave. Dependiendo de la categoría estructural de la aeronave (utilitario, aerobático, etc.) se diseñará para absorber estructuralmente factores de carga hasta un límite dado en ángulo de ataque positivo y otro límite en ángulo de ataque negativo. Una vez definidos estos, el diagrama V‑n completo denota una envolvente operativa en términos de límites de factor de carga.

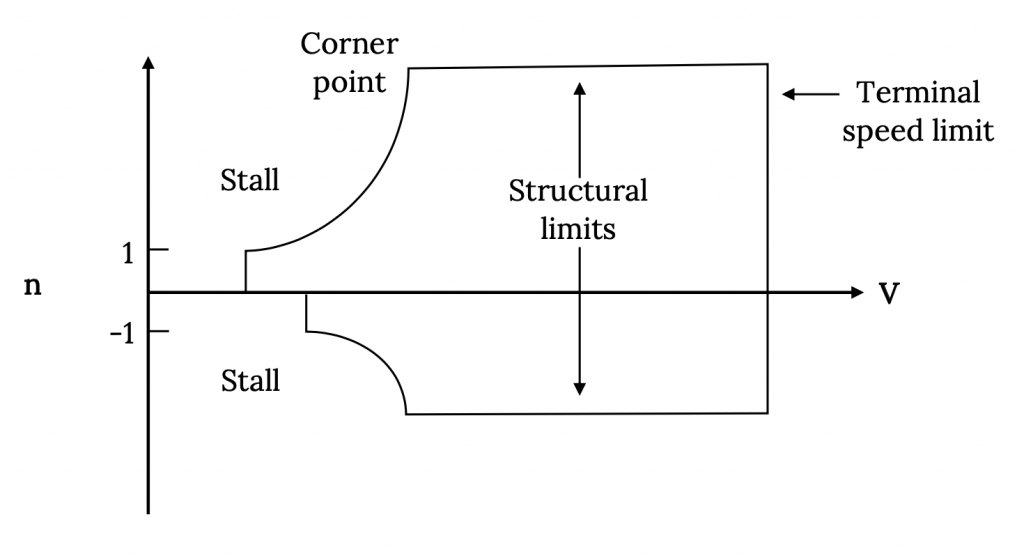
Se muestra la misma gráfica que antes, pero con líneas horizontales para los factores de carga máxima y mínima. La curva parabólica de calado gira horizontal en un punto de esquina, con las líneas horizontales dictadas por los límites estructurales de la aeronave. El factor de carga positiva máxima es notablemente mayor en magnitud que el factor de carga negativo mínimo, pero ambos terminan en una línea vertical denotada como el límite de velocidad del terminal. — Figura 8.8: Diagrama V-n completo

El punto donde se cruzan la línea límite estructural y el límite de calado se denomina “punto de esquina”. La velocidad en este punto está limitada tanto por el factor de carga estructural máximo como por el CLmax. La velocidad en ese punto es

$Vesquina= [(2nMaxW)/(ρCLmaxS)] 1/2$

A velocidades por debajo de la “velocidad de la esquina” es imposible dañar estructuralmente el avión aerodinámicamente porque el avión se detendrá antes de que se produzcan daños. A velocidades superiores a este valor es posible colocar la aeronave en una maniobra que resultará en daños estructurales, siempre que el avión tenga suficiente empuje para alcanzar esa velocidad y carga.

Es posible que una “ráfaga” de viento provoque cargas que excedan los límites anteriores. Tales ráfagas pueden ser parte de lo que se conoce como cizalladura del viento y son comunes alrededor de tormentas eléctricas o crestas de montaña. Las ráfagas pueden ser en dirección vertical u horizontal. El efecto primario de una ráfaga horizontal es aumentar o disminuir la probabilidad de pérdida debido al cambio de velocidad en relación con el ala. Esto suele ser la causa de los accidentes de cizalladura del viento alrededor de los aeropuertos donde la aeronave opera en condiciones cercanas a la parada.

Si una ráfaga es vertical, podemos ver su efecto en términos de cambio de ángulo de ataque. Supongamos que tenemos una ráfaga vertical de magnitud w _g. Su efecto sobre el ángulo de ataque y C _L se ve a continuación.

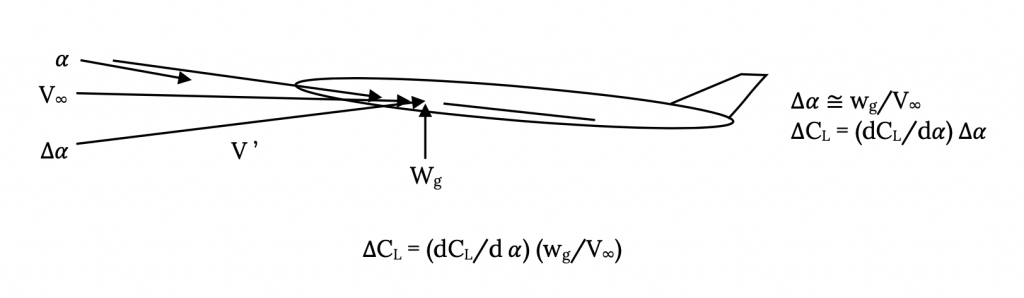
Un avión con un ángulo inicial de ataque alfa por encima de su límite de velocidad horizontal V sub infinito, está sujeto a una ráfaga que hace que la velocidad relativa se desplace en delta alfa por debajo de la horizontal a tope V primo. El límite de velocidad de ráfaga W sub g actúa verticalmente hacia arriba, resultando en un cambio en un cambio en el ángulo de ataque delta alfa que es aproximadamente igual a cap W sub g sobre cap V sub infinito. El cambio en el coeficiente de elevación, delta cap C sub cap L, es igual a d cap C sub cap L sobre d alfa por delta alfa. Estos se combinan para formar delta cap C sub cap L igual a d cap C sub cap L sobre d alpha times cap W sub g sobre cap V sub infinity. — Figura 8.9: Efecto de la carga de ráfaga sobre el coeficiente de elevación

por lo que el cambio en la elevación es

$ΔL=ΔCL (1/2ρV∞ 2S) 1/2 (DCL/Dα) ρSV∞ WG$

Así

$δN=δL/W= (1/W) 12DCl/DαρSV∞ WG$

Si, por ejemplo, una aeronave en vuelo recto y nivelado encuentra una ráfaga vertical de magnitud wg, el nuevo factor de carga es

$N′=N+δn=1+ (1/W) 1/2 (DCl/Dα) ρSV∞ WG$

(para vuelo recto y nivelado n = 1)

Por lo tanto, el efecto de la ráfaga sobre el factor de carga se amplifica por la velocidad de vuelo V. Este efecto se puede trazar en el diagrama V‑n para ver si resulta en pérdida o falla estructural.

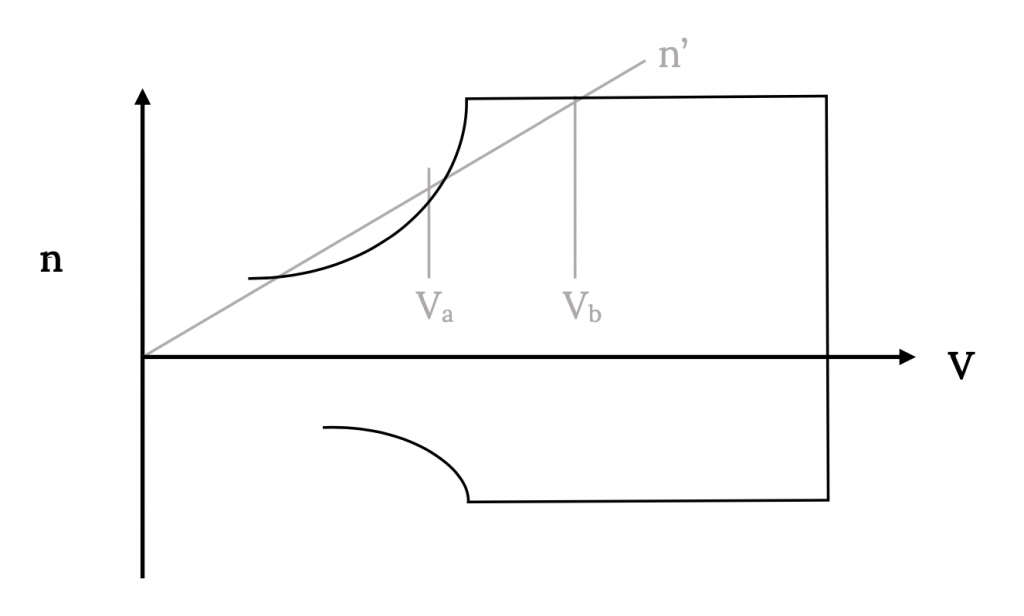
Se muestra la misma gráfica del diagrama cap V dash n, pero con una línea añadida n prime angulada por encima del eje V de la tapa. Pasa por el corte superior, saliendo a un valor de cap V sub a, luego pasando el límite estructural superior en cap V sub b. — Figura 8.10: Carga de ráfagas en diagrama V-n

_{Para el caso ilustrado anteriormente, la ráfaga provocará pérdida si ocurre a una velocidad de vuelo por debajo de Va y puede causar fallas estructurales si ocurre a velocidades superiores a V _b.}

Tarea 8

Deseamos comparar el desempeño de dos tipos diferentes de aviones “General Aviation”; el popular jet de negocios Cessna Citation III y el mejor plano integral, de cuatro lugares, monomotor, pistón en el negocio, el Cessna 182. Las características aerodinámicas y de rendimiento aproximadas se dan en la siguiente tabla:

Cuadro 8.1: Características aerodinámicas y de rendimiento

	CITACIÓN III	CESSNA 182
Envergadura	53.3 pies	35.8 pies
Área de ala	318 pies^2	174 pies^2
Peso bruto normal	19,815 lb	2,950 lb
Empuje total al nivel del mar	7300 lb	—
Potencia utilizable a nivel del mar	—	230 CV
C_D0	0.02	0.025
Factor de eficiencia de Oswald (e)	0.81	0.80

1. Calcular y tabular el empuje requerido (arrastre) versus los datos de V _e para ambas aeronaves y graficar los resultados en la misma gráfica [Figura 8.11]. Trazar las curvas disponibles de empuje a nivel del mar para ambas aeronaves en la misma gráfica [Figura 8.11].
2. Calcular la velocidad máxima al nivel del mar para ambas aeronaves y comparar con la que se indica en la gráfica [Figura 8.11].

El empuje y el arrastre se muestran en libras sobre el eje vertical, con incrementos de 1000 entre 0 y 8000. El eje horizontal es cap V sub e, con incrementos de 100 entre 0 y 1000. Círculos negros sólidos Empuje jet, círculos blancos representan arrastre Jet, cuadrados negros sólidos representan empuje prop, y cuadrados blancos representan arrastre prop. — Figura 8.11: Empuje y arrastre al nivel del mar

3. Calcular y tabular la potencia requerida frente a los datos de V _e para ambas aeronaves y trazar cada uno en una gráfica separada [Figuras 8.12 y 8.13]. Trazar la potencia del nivel del mar disponible en las mismas gráficas.
La potencia en caballos de fuerza se muestra en el eje vertical con incrementos de 100 hp entre 0 y 400, mientras que el límite de velocidad V en pies por segundo se muestra de 0 a 400 en incrementos de 100. Los círculos representan la potencia disponible, mientras que los cuadrados representan la potencia requerida.
Figura 8.12: Potencia a nivel del mar para Prop

La potencia en caballos de fuerza se muestra en el eje vertical con incrementos de 1000 hp entre 0 y 14 mil, mientras que el límite de velocidad V en pies por segundo se muestra de 0 a 1000 en incrementos de 100. Los círculos representan la potencia disponible, mientras que los cuadrados representan la potencia requerida.

8.13 Potencia a nivel del mar para Jet

4. Calcular y tabular la tasa de ascenso (en pies/min) versus los datos de velocidad a nivel del mar para ambas aeronaves para el peso bruto normal y trazar los datos en la misma gráfica [Figura 8.14]. El punto H en pies por minuto se muestra en el eje vertical en incrementos de 1000 entre 0 y 8 mil. Cap V sub e en pies por segundo se muestra en el eje horizontal en incrementos de 100 entre 0 y 1000. Los círculos representan apoyos, mientras que los cuadrados representan chorros.
Figura 8.14: Tasa de ascenso al nivel del mar para la cita III y C-182

5. Calcular y tabular la tasa máxima de ascenso versus datos de altitud para ambos aviones y trazarlo en la misma gráfica. [Figura 8.15]. Determinar los techos absolutos de ambas aeronaves.

La altitud h en pies se muestra sobre el eje vertical, en incrementos de 5000 entre 0 y 60 mil. El eje horizontal es h punto sub max en pies por minuto, con incrementos de 1000 entre 0 y 10 mil. Los círculos representan apoyos, mientras que los cuadrados representan chorros. — Figura 8.15: Tasa Máx de Subida vs Altitud Cessna-182, Cita III

6. Calcule el tiempo requerido para subir del nivel del mar a 20,000 pies para ambos aviones. Supongamos que las curvas (en 5) son lo suficientemente cercanas a lineales como para usar una aproximación lineal para el cálculo.

Referencias

Figura 8.1: Gris Kindred (2021). “Ángulo de giro”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.1-updated

Figura 8.2: Gris Kindred (2021). “” Patín para Girar” Usando Fuerza Lateral (a) Vista Superior (b) Vista Lateral.” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.2-updated

Figura 8.3: Gris Kindred (2021). “Giro Coordinado (a) Vista Superior (b) Vista en popa.” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.3-updated

Figura 8.4: Gris Kindred (2021). “Relación trigonométrica entre el ángulo de giro phi y el factor de carga n.” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.4_20210805

Figura 8.5: Gris Kindred (2021). “Indicador de giro y deslizamiento”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.5-updated

Figura 8.6: Gris Kindred (2021). “Porción de calado de un diagrama V-n (solo alfa positivo)”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.6-updated

Figura 8.7: Gris Kindred (2021). “Porción de parada completa del Diagrama V-n”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.7-updated

Figura 8.8: Gris Kindred (2021). “Diagrama V-n completo”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.8-updated

Figura 8.9: Gris Kindred (2021). “Efecto de la Carga de Ráfaga sobre el Coeficiente de Elevación” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.9-updated

Figura 8.10: Gris Kindred (2021). “Carga de Ráfagas en el Diagrama V-n”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/8.10-new

Figura 8.11: Gris Kindred (2021). “Empuje y arrastre al nivel del mar”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/hw-8-part-1

Figura 8.12: Gris Kindred (2021). “Poder a Nivel del Mar Para Prop.” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/hw-8-part-2

Figura 8.13: Gris Kindred (2021). “Poder a Nivel del Mar Para Chorro”. CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/hw-8-part-3

Figura 8.14: Gris Kindred (2021). “Tasa de Subida a Nivel del Mar para la Cita III y C-182.” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/hw-8-part-4

Figura 8.15: Gris Kindred (2021). “Tasa Máx de Subida vs Altitud Cessna-182, Cita III.” CC BY 4.0. Adaptado de James F. Marchman (2004). CC BY 4.0. Disponible en https://archive.org/details/hw-8-part-5

<! — pb_fixme —><! — pb_fixme —>

Search

Text Color

Text Size

Margin Size

Font Type

Ejemplo\(\PageIndex{1}\)