3.2: Determinar una distribución en ausencia de datos

A menudo, los valores de los parámetros para las distribuciones de probabilidad utilizadas para modelar cantidades aleatorias deben determinarse en ausencia de datos. Hay muchas razones posibles para la falta de datos. El estudio de simulación puede involucrar un sistema propuesto. Por lo tanto, no existe ningún dato. El tiempo y el costo requeridos para obtener y analizar datos pueden estar fuera del alcance del estudio. Esto podría ser especialmente cierto en la fase inicial de un estudio donde se va a construir un modelo inicial y analizar las alternativas iniciales en poco tiempo. Es posible que el equipo de estudio no tenga acceso al sistema de información donde residen los datos.

Se presentan las funciones de distribución comúnmente empleadas en ausencia de datos. Se da una ilustración de cómo seleccionar una distribución particular para modelar una cantidad aleatoria en este caso.

3.2.1 Funciones de distribución utilizadas en ausencia de datos

La mayoría de las veces, los diseñadores de sistemas u otros expertos tienen una buena comprensión del valor “promedio”. A menudo, lo que quieren decir con “promedio” es realmente el valor o modo más probable. Además, con mayor frecuencia pueden suministrar estimaciones razonables de los límites inferior y superior que son los valores mínimo y máximo. Por lo tanto, se deben usar funciones de distribución que tengan un límite inferior y superior y cuyos parámetros se puedan determinar utilizando no más información que un límite inferior, un límite superior y un modo.

Primero considere las funciones de distribución utilizadas para modelar los tiempos de operación. La distribución uniforme requiere sólo dos parámetros, el mínimo y el máximo. Solo se permiten valores en este rango [min, max]. Todos los valores entre el mínimo y el máximo son igualmente probables. Normalmente, se dispone de más información sobre un tiempo de operación como el modo. Sin embargo, si solo se dispone del mínimo y el máximo se puede utilizar la distribución uniforme.

La Figura 3-1 proporciona un resumen de la distribución uniforme.

Figura 3-1: Resumen de la Distribución Uniforme

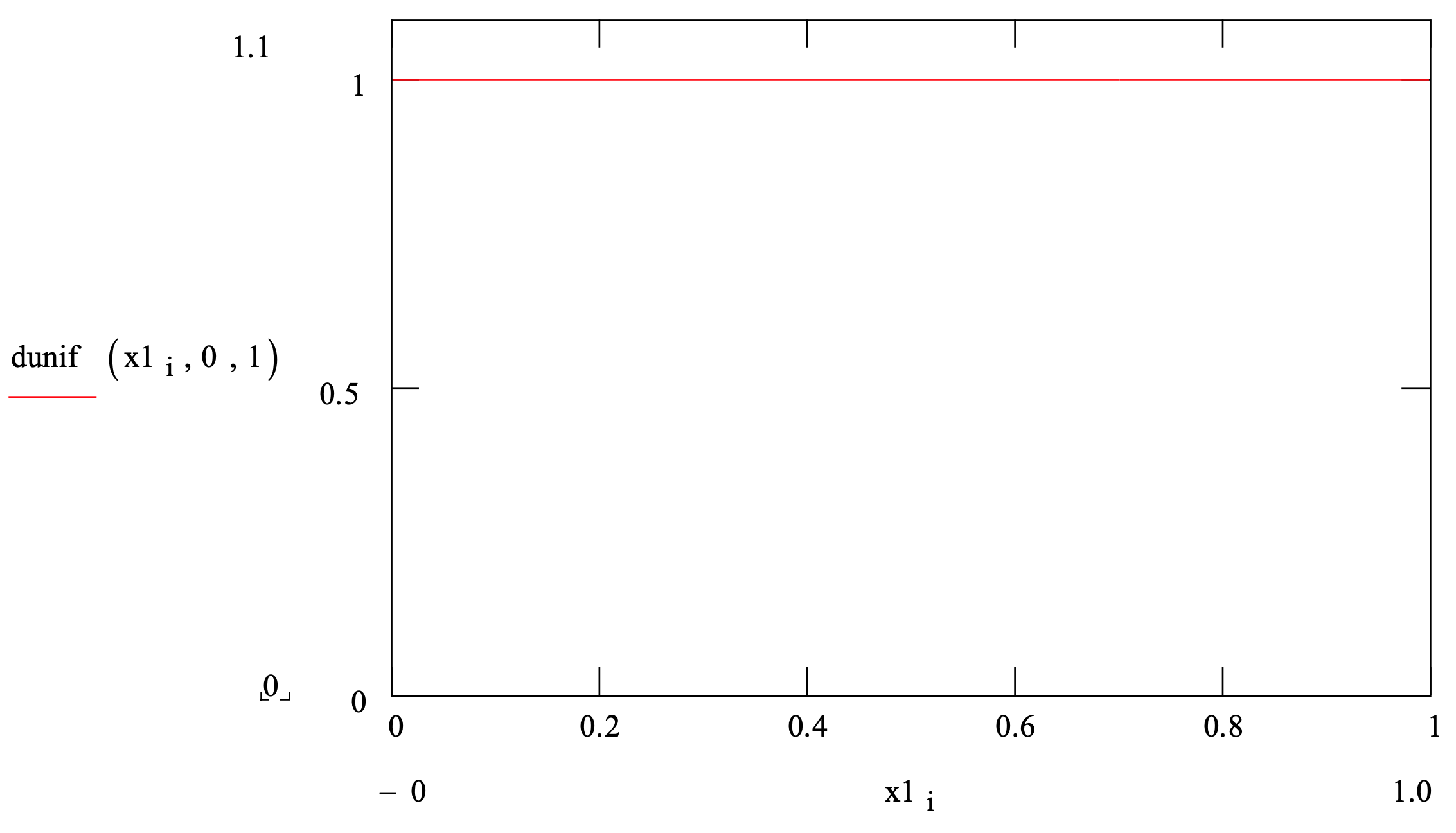
Ilustración de la función de densidad

Parámetros:	min (imum) y max (imum)
Rango:	[min, max]
Media:	\(\ \text { mean }=\frac{\min +\max }{2}\)
Varianza:	\(\ \text { variance }=\frac{(\max -\min )^{2}}{12}\)
Función de densidad:	\(\ f(x)=\frac{1}{\max -\min } ; \min \leq x \leq \max\)
Función de distribución:	\(\ F(x)=\frac{x-\min }{\max -\min } ; \min \leq x \leq \max\)
Aplicación:	A falta de datos, la distribución uniforme se utiliza para modelar una cantidad aleatoria cuando solo se pueden estimar el mínimo y el máximo.

Si el modo también está disponible, se puede usar la distribución triangular. El mínimo, el máximo y el modo son los parámetros de esta distribución. Tenga en cuenta que el modo puede estar más cerca del mínimo que del máximo para que la distribución esté sesgada a la derecha. Alternativamente, la distribución puede estar sesgada hacia la izquierda para que el modo esté más cerca del máximo que el mínimo. La distribución puede ser simétrica con el modo equidistante del mínimo y el máximo. Estos casos se ilustran en la Figura 3-2 donde se da un resumen de la distribución triangular.

Figura 3-2: Resumen de la Distribución Triangular

Parámetros:	min (imum), modo y max (imum)
Rango:	[min, max]
Media:	\(\ \frac{min +mode +max }{3}\)
Varianza:	\(\ \frac{min^2 +mode^2 +max^2 -min * mode \ -min *max -mode * max }{18}\)
Función de densidad:	\ (\ f (x) =\ left\ {\ begin {array} {cc} \ frac {2^ {*} (\ mathbf {x} -\ mathbf {m i n})} {(\ max -\ min) * (\ nombreoperador {modo} -\ min)};\ min\ leq\ mathbf {x}\ leq\ nombreoperador {modo}\ \ frac {2^ {*} (\ max -\ mathbf {x})} {(\ max -\ min) * (\ max -\ nombreoperador {modo})};\ nombredeoperador { mode} <\ mathbf {x} <\ max \ end {array}\ right\}\)
Función de distribución:	\ (\ F (x) =\ izquierda\ {\ comenzar {array} {lc} \ frac {(x-m i n) ^ {2}} {(\ max -m i n) * (m o d e-m i n)};\ min\ leq x\ leq\ texto {modo}\\ 1-\ frac {(\ max -x) ^ {2}} {(\ -max m i n) * (\ max -m o d e)};\ texto {modo} <x<\ max. \ end {array}\ derecha\}\)
Aplicación:	A falta de datos, la distribución triangular se utiliza para modelar una cantidad aleatoria cuando se puede estimar el valor más probable así como el mínimo y el máximo.

La distribución beta proporciona otra alternativa para modelar un tiempo de operación en ausencia de datos. La función de densidad de distribución triangular está compuesta por dos líneas rectas. La función de densidad de distribución beta es una curva suave. Sin embargo, la distribución beta requiere más información y cómputos para usar que la distribución triangular. Además, la distribución beta se define en el rango [0,1] pero se puede cambiar y escalar fácilmente al rango [min, max] usando min + (max-min) *X, donde X es una variable aleatoria distribuida beta en el rango [0, 1]. Así, al igual que las distribuciones uniforme y triangular, la distribución beta puede ser utilizada para valores en el rango [min, max].

El uso de la distribución beta requiere valores tanto para el modo como para la media. Se pueden obtener estimaciones subjetivas de ambas cantidades. Sin embargo, suele ser más fácil obtener una estimación del modo que la media. En este caso, la media se puede estimar a partir de los otros tres parámetros utilizando la ecuación 3-1.

\(\ \begin{align}mean = \frac{min + mode + max}{3}\tag{3-1}\end{align}\)

Pritsker (1977) da una ecuación alternativa que es similar a la ecuación 3-2 excepto que el modo se multiplica por 4 y el denominador es por lo tanto 6.

Los dos parámetros de la distribución beta son\(\ \alpha_{1}\) y\(\ \alpha_{2}\). Estos se calculan a partir del mínimo, máximo, modo y media usando las ecuaciones 3-2 y 3-3.

\(\ \begin{align}\alpha_{1}=\frac{(\mathrm{mean}-\min ) *(2 * \mathrm{mode}-\min -\mathrm{max})}{(\mathrm{mode}-\operatorname{mean}) *(\max -\min )}\tag{3-2}\end{align}\)

\(\ \begin{align}\alpha_{2}=\frac{(\max -\operatorname{mean}) * \alpha_{1}}{\operatorname{mean}-\min }\tag{3-3}\end{align}\)

La mayoría de las veces para tiempos de operación,\(\ \alpha_{1}\) 1 y\(\ \alpha_{2}\) > 1. Al igual que la distribución triangular, la distribución beta puede estar sesgada a la derecha\(\ \alpha_{1}<\alpha_{2}\), sesgada a la derecha\(\ \alpha_{1}>\alpha_{2}\), o simétrica,\(\ \alpha_{1}=\alpha_{2}\). En la Figura 3-3 se presenta un resumen de estas y otras características de la distribución beta.

A continuación, considere modelar el tiempo entre llegadas de entidades. A falta de datos, todo lo que puede conocerse es el número promedio de entidades que se espera que lleguen en un intervalo de tiempo determinado. Los siguientes supuestos suelen ser razonables cuando no se dispone de datos.

1. Las entidades llegan una a la vez.
2. El tiempo medio entre llegadas es el mismo en todos los tiempos de simulación.
3. El número de clientes que llegan en intervalos de tiempo disgregados es independiente.

Todo ello lleva a utilizar la distribución exponencial para modelar los tiempos entre llegadas. El exponencial tiene un parámetro, su media. La varianza es igual a la media al cuadrado. Así, la media es igual al tiempo medio entre llegadas o el intervalo de tiempo de interés dividido por una estimación del número de llegadas en ese intervalo.

El uso de la distribución exponencial en este caso puede considerarse un enfoque conservador como lo discuten Hopp y Spearman (2007). Estos autores se refieren a un sistema con tiempos distribuidos exponencialmente entre llegadas y tiempos de servicio como el peor de los casos prácticos. Este término se utiliza para expresar la creencia de que cualquier sistema con peor desempeño tiene una necesidad crítica de mejora. A falta de datos en contrario, suponer que las llegadas a un sistema en estudio no son peores que en el peor caso práctico parece seguro.

La Figura 3-4 resume la distribución exponencial.

Figura 3-3: Resumen de la distribución beta

Ilustraciones de la función

Parámetros:	min (imum), modo, media y max (imum)
Rango:	[min, max]
Media:	\(\ \frac{\alpha_{1}}{\alpha_{1}+\alpha_{2}}\)
Varianza:	\(\ \frac{\alpha_{1}\ {*}\ \alpha_{2}}{\left(\alpha_{1}+\alpha_{2}\right)^{2} *\left(\alpha_{1}+\alpha_{2}+1\right)}\)
Función de densidad:	\(\ f(x)=\frac{x^{\alpha_{1}-1}(1-x)^{\alpha_{2}-1}}{B\left(\alpha_{1}, \alpha_{2}\right)} ; 0<x<1\)
	El denominador es la función beta.
Función de distribución:	Sin forma cerrada.
Aplicación:	En ausencia de datos, la distribución beta se utiliza para modelar una cantidad aleatoria cuando se puede estimar el mínimo, el modo y el máximo. Si está disponible, también se puede usar una estimación de la media o la media se puede calcular a partir del mínimo, modo y máximo. Tradicionalmente, la distribución beta se ha utilizado para modelar el tiempo para completar una tarea de proyecto. Cuando se dispone de datos, la beta se puede utilizar para modelar la fracción, del 0 al 100%, de algo que tiene cierta característica como la fracción de chatarra en un lote.

Figura 3-4: Resumen de la distribución exponencial

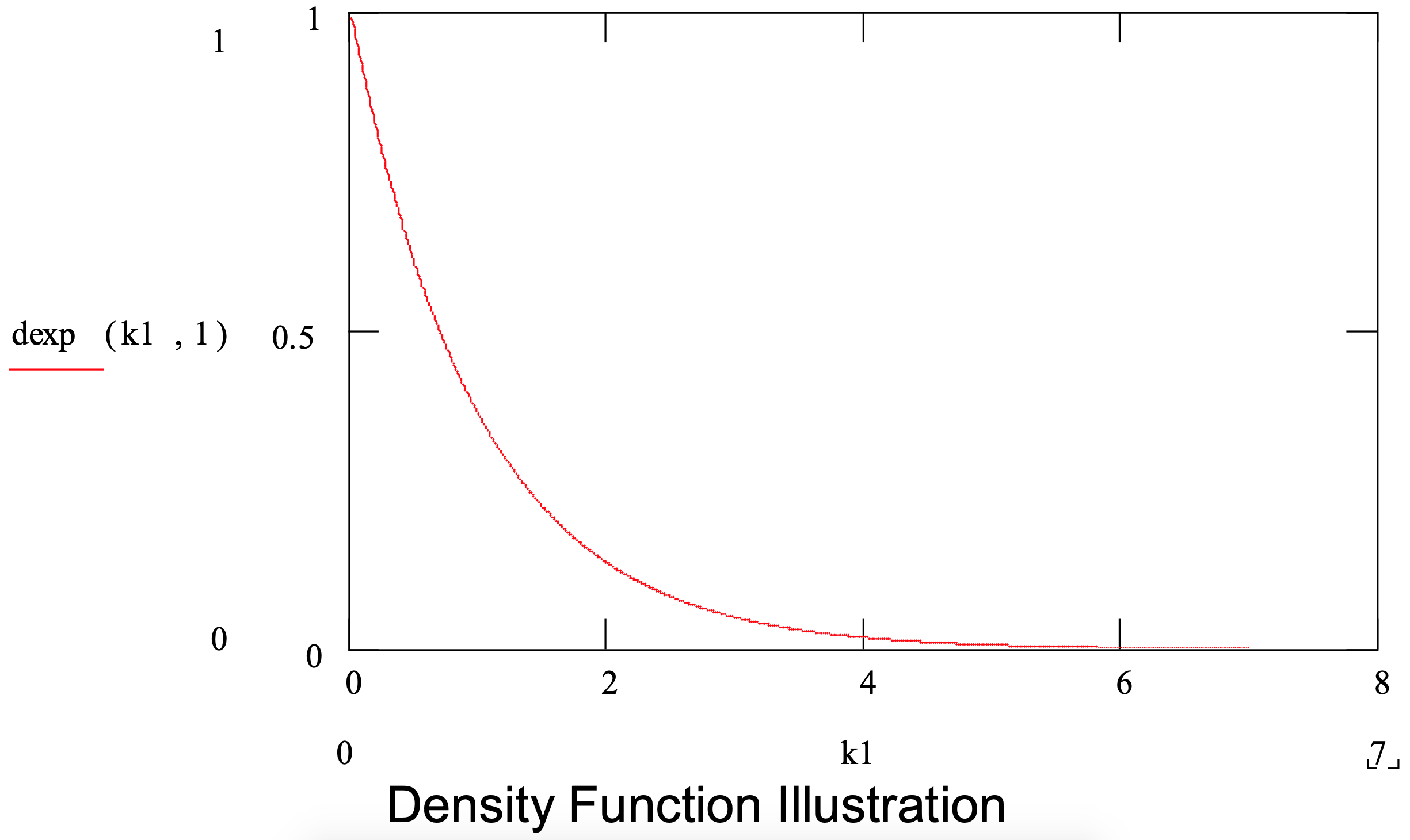
Parámetro:	media
Rango:	[0,\(\ \infty\))
Media:	parámetro dado
Varianza:	media ^2
Densityfunction:	\(\ f(x)=\frac{1}{\text { mean }} e^{-x / \text {mean}} ; x \geq 0\)
Función de distribución:	\(\ F(x)=1-e^{-x / \text {mean}} ; x \geq 0\)
Aplicación:	El exponencial se utiliza para modelar cantidades con alta variabilidad, tales como tiempos de inter-llegada de entidades y el tiempo entre fallas de equipos, así como tiempos de operación con alta variabilidad. En ausencia de datos, la distribución exponencial se utiliza para modelar una cantidad aleatoria caracterizada únicamente por la media.

3.2.2 Selección de distribuciones de probabilidad en ausencia de datos — Una ilustración

Considere el tiempo de operación para una sola estación de trabajo. Supongamos que las estimaciones de un modo de 7 segundos, un mínimo de 5 segundos y un máximo de 13 segundos fueron aceptadas por el equipo del proyecto. Se podría seleccionar cualquiera de las dos distribuciones.

1. Un triangular con los valores de los parámetros dados y que tiene un coeficiente de variación al cuadrado ¹ de 0.042.
2. Una distribución beta con valores de parámetros\(\ \alpha_{1}\) = 1.25 y\(\ \alpha_{2}\) = 1.75 y un coeficiente de variación cuadrado de 0.061 donde se utilizaron las ecuaciones 3-3 y 3-4 para calcular\(\ \alpha_{1}\) y\(\ \alpha_{2}\).

La media de la distribución beta se estimó como la media aritmética del mínimo, máximo y modo. Así, la media de la distribución triangular y de la distribución beta son las mismas.

Obsérvese que la elección de distribución podría afectar significativamente los resultados de la simulación ya que el coeficiente de variación cuadrado de la distribución beta es aproximadamente 150% del de la distribución triangular. Esto significa que el tiempo promedio en el búfer en la estación de trabajo A probablemente será más largo si se usa la distribución beta en lugar de la triangular. Esta idea se discutirá más a fondo en el Capítulo 5.

La Figura 3-5 muestra las funciones de densidad de estas dos distribuciones.

Figura 3-5: Funciones de Densidad de Probabilidad del Triangular (5, 7, 13) y Beta (1.25, 1.75)

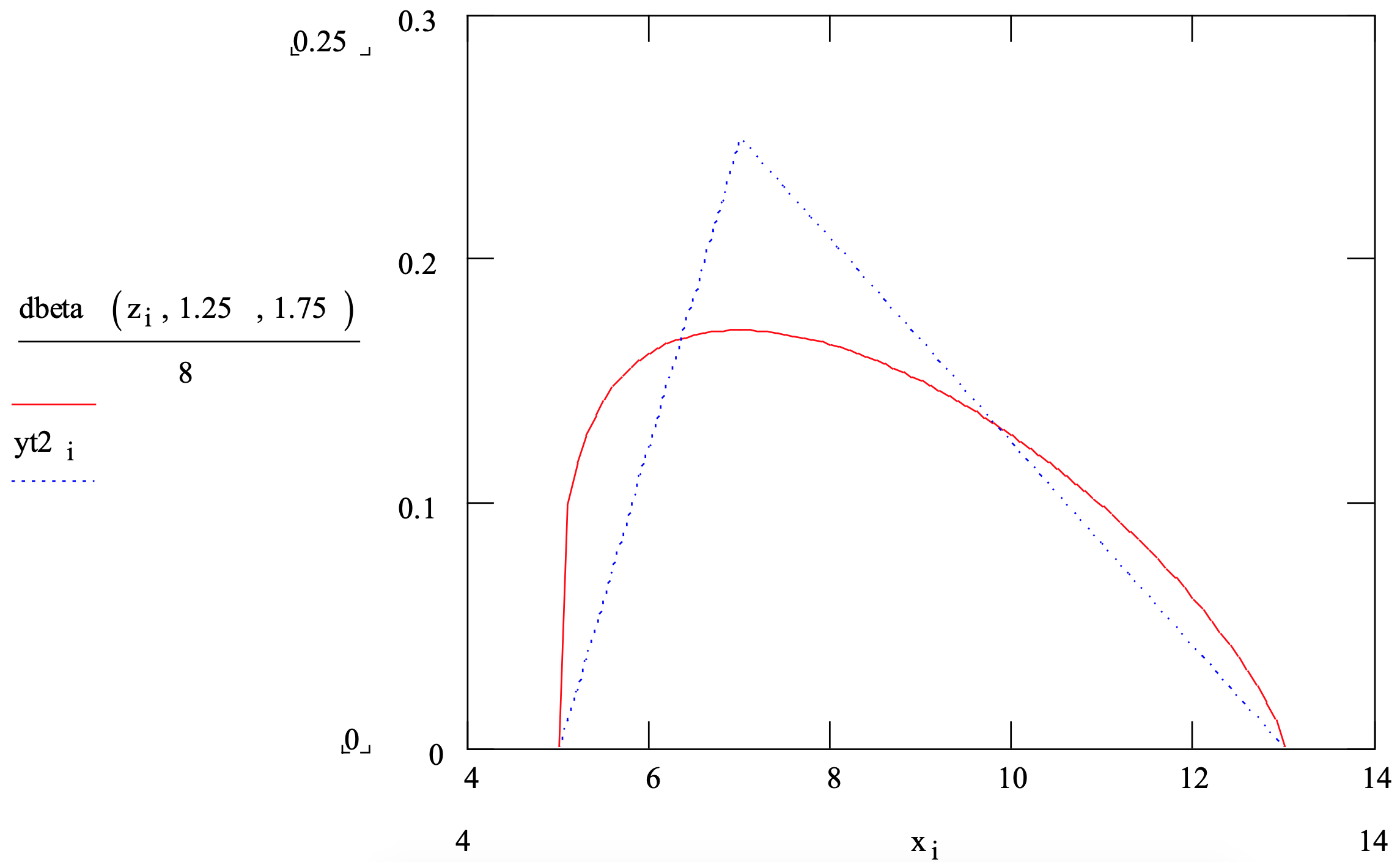
Una palabra de precaución está en orden. Si no hay razón de peso para elegir la distribución triangular o beta, entonces un curso de acción conservador sería ejecutar la simulación primero usando una distribución y luego la otra. Si no hay diferencia significativa en los resultados de la simulación o al menos en las conclusiones del estudio, entonces no se necesita ninguna acción adicional. Si la diferencia en los resultados es significativa, tanto operativa como estadísticamente, se debe recopilar y estudiar más información y datos sobre la cantidad aleatoria que se está modelizando.

---

¹ El coeficiente de variación es la desviación estándar dividida por la media. Cuanto menor sea esta cantidad, mejor.

---

Además, se estimó que habría 14400 llegadas por semana de 40 horas a las dos estaciones de trabajo en un sistema en serie. Así, el tiempo promedio entre llegadas es de 40 horas/14400 llegadas = 10 segundos. El tiempo entre llegadas se modeló usando una distribución exponencial con media de 10 segundos.