13.7: Ocasionalmente ¿Casino deshonesto? Cadenas Markov y modelos ocultos de Markov

Última actualización
Guardar como PDF

Page ID: 85467

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Introducción

La probabilidad básica se puede usar para predecir eventos simples, como la probabilidad de que una moneda lanzada aterrice en la cabeza en lugar de en la cola. Instintivamente, podríamos decir que hay un 50% de posibilidades de que la moneda aterrice sobre cabezas.

Pero digamos que acabamos de ver la misma moneda aterrizar en cabezas cinco veces seguidas, ¿seguiríamos diciendo que hay un 50% de probabilidad de que el sexto lanzamiento de moneda resulte en cabezas? No —intuitivamente, percibimos que hay una probabilidad muy baja (mucho menos del 50%) de que la moneda aterrice en cabezas seis veces seguidas.

¿Qué nos hace repensar la probabilidad de que la moneda aterrice sobre cabezas? Se está lanzando la misma moneda, pero ahora estamos tomando en cuenta los resultados de tiradas anteriores. La probabilidad básica se puede utilizar para predecir un evento aislado. Pero se deben utilizar conceptos de probabilidad más avanzados para evaluar la probabilidad de que ocurra una determinada secuencia de eventos. Esta sección proporciona una introducción a conceptos como la regla de Bayes, las cadenas de Markov y los modelos ocultos de Markov, que son más útiles para predecir escenarios del mundo real (que rara vez son singulares, eventos aislados).

Regla de Bayes

La regla de Bayes es un concepto fundamental para encontrar la probabilidad de series de eventos relacionados. Se relaciona la probabilidad de evento A condicional con el evento B y la probabilidad de evento B condicional al evento A, que a menudo no son las mismas probabilidades.

\[P(A | B)=\frac{P(B | A) P(A)}{P(B)} \nonumber \]

Otra interpretación de la regla de Bayes: es un método para actualizar o revisar creencias (es decir, probabilidad de aterrizar en cabezas) a la luz de nuevas pruebas (sabiendo que la moneda aterrizó en cabezas los últimos cinco lanzamientos).

Cadenas Markov

Una cadena de Markov es una forma particular de modelar la probabilidad de una serie de eventos. Una cadena de Markov es una secuencia de valores aleatorios cuyas probabilidades en un intervalo de tiempo dependen únicamente del valor del número en el tiempo anterior. Una cadena de Markov, que lleva el nombre de Andrey Markov, es un proceso estocástico con la propiedad de Markov. Esto quiere decir que, dado el estado presente, los estados futuros son independientes de los estados pasados. En otras palabras, la descripción del estado presente captura completamente toda la información que podría influir en la evolución futura del proceso, de manera que los estados futuros del sistema se alcanzarán a través de un proceso probabilístico (determinado a partir de datos actuales) en lugar de uno determinista (a partir de datos pasados).

En cada momento, el sistema podría o bien cambiar su estado del estado actual a un estado diferente, o bien permanecer en el mismo estado. Esto sucede de acuerdo con la distribución de probabilidad especificada. Estos cambios de estado se llaman transiciones, y las probabilidades asociadas con diversos cambios de estado se denominan probabilidades de transición.

Por ejemplo, digamos que queremos saber la probabilidad de que un elevador se mueva más de cinco pisos hacia arriba en un edificio de 30 pisos (incluido el lobby). Este es un ejemplo de una cadena de Markov porque la probabilidad no depende de si el elevador estaba en el piso 6 a las 7:00am o en el piso 27 a las 10:30pm. En cambio, la probabilidad depende de en qué piso se encuentre el elevador justo antes de que comience a moverse. Más específicamente, el hecho de que el elevador esté en el último piso$t_1$ da como resultado una probabilidad cero de que el elevador sea cinco pisos más alto en$t_2$.

La siguiente figura ayuda a visualizar el concepto de un Modelo Markov.

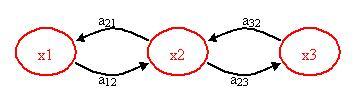
x ₁, x ₂, x ₃ = estados

a ₁₂, a ₂₁, a ₂₃, a ₃₂ = probabilidades de transición

Una probabilidad de transición es simplemente la probabilidad de pasar de un estado a otro estado. Tenga en cuenta que puede haber otras rutas o probabilidades de transición para el estado x ₁, digamos al estado x ₃ o de vuelta a sí mismo. La suma de las probabilidades de transición siempre debe ser igual a 1.

\[a_{1, i}=a_{11}+a_{12}+a_{13}+\ldots a_{1 n} \nonumber \]

\[\sum_i=1 \nonumber \]

Probabilidad de Transición

Las probabilidades de transición de cada estado para un sistema se pueden compilar en una matriz de transición. La matriz de transición para un sistema puede representar una transición de un paso o una transición de varios pasos. Una matriz de transición de n pasos es simplemente una matriz de transición de un solo paso elevada a la enésima potencia.

Para que el estado i haga una transición al estado j, la probabilidad de transición P _i j debe ser mayor que 0. así:

\[P_{i, j} \geq 0, i, j \geq 0 \nonumber \]

\[\sum_{j=0} P_{ij} = 1 \nonumber \]

con$i$ = 0, 1,...

Sea P la matriz de una matriz de transición de un solo paso,

P =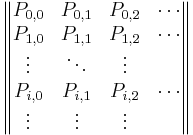 $begin {Vmatrix} P_ {0,0} & P_ {0,1} & P_ {0,2} &\ cdots\\ P_ {1,0} & P_ {1,1} & P_ {1,2} &\ cdots\ \ vdots &\ ddots &\ vdots\\ p_ {i,0} & P_ {i,1} & P_ {i,2} &\ cdots\\ vdots \\ puntos &\ vdots &\ vdots \ end {Vmatrix}$

$P_{i,1}$denotaría la probabilidad de pasar del estado i al 1

Ejemplo$\PageIndex{1}$: Will It Rain Tomorrow?

Supongamos que el que llueva o no hoy depende de las condiciones climáticas previas a lo largo de los dos últimos días. Específicamente, supongamos que si ha llovido durante los dos últimos días, entonces lloverá mañana con probabilidad 0.7; si llovió hoy pero no ayer, entonces lloverá mañana con probabilidad 0.5; si llovió ayer pero no hoy, entonces lloverá mañana con probabilidad 0.4; si no ha llovido en los dos últimos días, entonces lloverá mañana con probabilidad 0.2.

Solución

La matriz de transición para el sistema anterior sería:

estado 0: si llovió tanto hoy como ayer
estado 1: si llovió hoy pero no ayer
estado 2: si llovió ayer pero no hoy
estado 3: si no llovió ni ayer ni hoy

\ [\ mathbf {P} =\ izquierda|\ begin {array} {cccc}
0.7 & 0 & 0.3 & 0\\
0.5 & 0 & 0 & 0.5 & 0 & 0\\
0 & 0.4 & 0 & 0 & 0.6\\
0 & 0.2 & 0 & 0.8\ derecha|
\ end {array}\ nonumber\]

Aplicaciones de las Cadenas Markov

Dado que este concepto es bastante teórico, son necesarios ejemplos de aplicaciones de esta teoría para explicar el poder que tiene esta teoría. Aunque estas siguientes aplicaciones no están relacionadas con el control químico, tienen mérito en explicar la diversidad de operaciones en las que se pueden utilizar las cadenas de Markov. Ojalá, al ver estos ejemplos, el lector podrá utilizar las cadenas de Markov en nuevos enfoques creativos para resolver problemas de controles químicos.

Teoría de colas

Las cadenas de Markov se pueden aplicar para modelar varios elementos en algo llamado teoría de colas. La teoría de colas es simplemente el estudio matemático de las líneas de espera (o colas).

Esta teoría permite el análisis de elementos que llegan al fondo de la línea, esperan en la fila y son procesados (o servidos) al frente de la línea. Este método utiliza las variables que incluyen el tiempo promedio de espera en la cola o el sistema, el número esperado esperando o recibiendo el servicio y la probabilidad de encontrarse con el sistema en ciertos estados, como vacío, lleno, tener un servidor disponible o tener que esperar cierto tiempo para ser atendido. Todas estas variables son únicas para el sistema en cuestión. Un enlace que explica esta teoría con más detalle se puede encontrar a continuación:

Teoría de colas

Aunque la teoría de colas se usa generalmente en aplicaciones de servicio al cliente, logística y operaciones, se puede adaptar al procesamiento químico. Por ejemplo, es esencial modelar cuánto tiempo estará un producto en particular en una línea de ensamblaje antes de que llegue al proceso final deseado. Así, esta teoría es robusta para todo tipo de usos.

Ejemplo$\PageIndex{1}$: Queuing Problem

En una soleada mañana de martes en el Edificio de Ingeniería Informática, un grupo de estudiantes de Ingeniería Química están terminando sus informes de laboratorio de ingeniería y se han quedado despiertos toda la noche escribiendo preguntas ambivalentes de mecánica de fluidos, necesitan un café de prestigio para refrescarse en lugar de Red Bull. La cafetería llamada “Dreamcast's Cafè” fue inaugurada por un graduado de Ingeniería Química de la Universidad de Michigan. Los negocios van muy bien para “Dreamcast's Cafè” y hay mucha gente, m gente, esperando en fila frente a los estudiantes de Ingeniería Química. El tiempo de servicio para la primera persona en línea (no necesariamente estudiante de Ingeniería Química) es una distribución exponencial con un tiempo de espera promedio de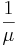 $\ frac {1} {\ mu}$ . Dado que los estudiantes de Ingeniería Química tienen que regresar al Edificio de Ingeniería en Computación para terminar su reporte, tienen una paciencia finita esperando en fila y su paciencia es una distribución exponencial con un promedio de 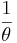$\ frac {1} {\ theta}$ . Al grupo de estudiantes de Ingeniería Química no le importa qué tan largo sea el tiempo de servicio. Encuentra la probabilidad de que el estudiante i-ésimo de Ingeniería Química espere lo suficiente para tomar café.

Solución

ueuing Problem.jpg

Agrega texto aquí.

Sistema de clasificación de páginas de Google

El PageRank de una página web utilizada por Google está definido por una cadena de Markov. PageRank es la probabilidad de estar en la página$i$ en la siguiente cadena de Markov en todas las páginas web (conocidas). Si N es el número de páginas web conocidas, y una página$i$ tiene$k_i$ enlaces, entonces tiene probabilidad de transición

\[\dfrac{(1 − q)}{ki} + \dfrac{q}{N} \nonumber \]

para todas las páginas que están enlazadas y$q/N$ para todas las páginas que no están enlazadas. La constante$q$ es de alrededor de 0.15.

Juegos Infantiles

Las cadenas de Markov se utilizan en los juegos infantiles “Chutes and Ladders”, “Candy Land” y “Hi Ho! ¡Cereza-O!” Estos juegos utilizan el concepto de Markov de que cada jugador inicia en una posición determinada en el tablero de juego al comienzo de cada turno. A partir de ahí, el jugador tiene probabilidades fijas de moverse a otras posiciones.

Para entrar en más detalles, cualquier versión de Snakes and Ladders puede representarse exactamente como una cadena de Markov, ya que desde cualquier cuadrado las probabilidades de moverse a cualquier otra casilla son fijas e independientes de cualquier historial de juego anterior. La versión Milton Bradley de Chutes and Ladders cuenta con 100 cuadrados, con 19 canaletas y escaleras. Un jugador necesitará un promedio de 45.6 giros para pasar del punto de partida, que está fuera del tablero, al cuadrado 100.

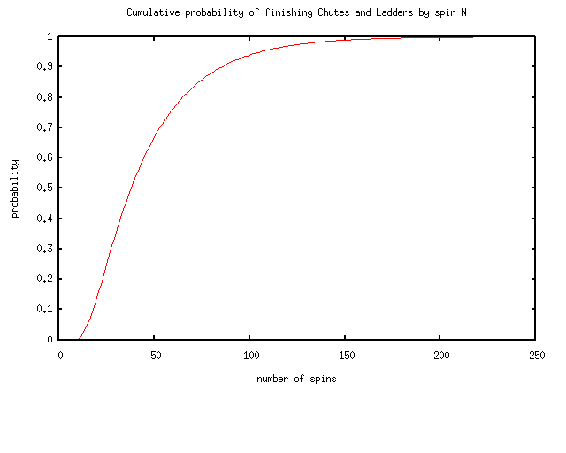
I Prob.gif

Un último juego de interés es Monopoly. Esto se puede modelar usando cadenas de Markov. Consulta el siguiente enlace para ver una simulación de la probabilidad de aterrizar en una propiedad en particular en el juego Monopoly:

Simulación de monopolio

Modelos ocultos de Markov

Construyendo más en el concepto de una cadena de Markov se encuentra el modelo oculto de Markov (HMM). Un modelo oculto de Markov es un modelo estadístico donde se asume que el sistema que se modela es un proceso de Markov con parámetros desconocidos o eventos casuales. Los HMM son principalmente útiles para determinar los parámetros ocultos a partir de los parámetros observables.

Nuevamente, la siguiente figura puede ayudar a visualizar el concepto del modelo oculto de Markov.

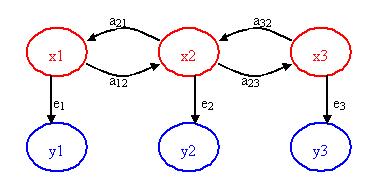
x ₁, x ₂, x ₃ = estados ocultos/desconocidos

a ₁₂, a ₂₁, a ₂₃, a ₃₂ = probabilidades de transición

y ₁, y ₂, y ₃ = estados observables

e ₁, e ₂, e ₃ = probabilidades de emisión

El punto clave de la figura anterior es que solo se ven los círculos azules, pero se sospecha o sabe que estos estados observables están directamente relacionados o dependen de algún estado oculto. Estos estados ocultos (los círculos rojos) son lo que en realidad dicta el resultado de los estados observables. El reto es averiguar los estados ocultos, las probabilidades de emisión y las probabilidades de transición.

Por ejemplo, digamos que tiene un programa de adquisición de datos que registra continuamente la temperatura de salida de su flujo de productos que está calentando a través de un intercambiador de calor. El intercambiador de calor proporciona un suministro constante de calor. Se observa que la temperatura tiene algunas perturbaciones escalonadas y no siempre es constante. La temperatura es el parámetro observable, pero la causa de sus desviaciones/estados es en realidad el caudal de la corriente. Cuando el caudal fluctúa, la temperatura de salida también fluctúa ya que el intercambiador de calor proporciona la misma cantidad de calor a la corriente. Entonces, el caudal de corriente es el parámetro oculto (ya que no tiene acceso a esta variable medida) y la probabilidad de que los caudales cambien de digamos 100 a 150 a 300 L/h son las probabilidades de transición. La probabilidad de emisión es la probabilidad de que la temperatura de salida observada sea causada directamente por el caudal. Esta probabilidad de emisión no es necesariamente 1 ya que las variaciones de temperatura también podrían deberse al ruido, etc.

Otro escenario común utilizado para enseñar el concepto de un modelo oculto de Markov es el “Casino Ocasionalmente Deshonesto”. Si un casino usa un dado justo, cada número tiene una probabilidad de 1/6 de ser aterrizado. Este tipo de probabilidad que representa un parámetro conocido se conoce como probabilidad de emisión en HMM. A veces un casino puede inclinar las probabilidades usando un dado cargado, donde un número es favorecido sobre los otros cinco números y por lo tanto el lado que se favorece tiene una probabilidad que es mayor que 1/6.

Pero, ¿cómo se sabe que el casino está siendo deshonesto al usar un dado cargado? Pretende que el dado esté cargado de tal manera que favorezca al número 6. Sería difícil diferenciar entre un dado justo y un dado cargado después de ver solo un rollo. Es posible que puedas hacerte una mejor idea después de ver algunos tiradas y ver cuántas veces aterrizó el dado en 6. Digamos que viste la siguiente secuencia de tiradas de troqueles:

465136

Todavía es difícil decir con certeza si el dado está cargado o no. La secuencia anterior es factible tanto para una matriz justa como para una matriz cargada. En este caso particular, los números anteriores que representan lo que se rodó son los parámetros observables. El parámetro oculto es el tipo de dado usado solo porque no sabemos qué tipo produjo la secuencia de números anterior.

En lugar de confiar en una sospecha furtiva de que el casino está siendo deshonesto, se puede usar un modelo oculto de Markov para demostrar que ocasionalmente se usa un dado cargado. Tenga en cuenta que si se usaba un dado cargado todo el tiempo, sería más evidente. Para salirse con la suya con esta “leve” injuria, el casino cambiará el dado justo por uno cargado de vez en cuando. Digamos que si se está utilizando un dado justo hay un 5% de posibilidades de que se cambie a un dado cargado y un 95% de probabilidad de que siga siendo justo. Estas son conocidas como probabilidades de transición porque representan la probabilidad de que un evento causal cambie a otro evento causal.

A continuación se muestra una imagen que representa las probabilidades de transición (probabilidad de permanecer o cambiar un tipo de dado) así como las probabilidades de emisión (probabilidad de aterrizar en un número).

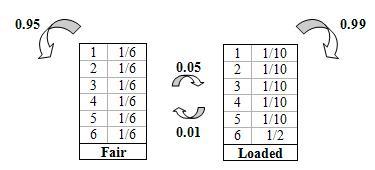
Usando el diagrama básico anterior que muestra las propiedades de emisión y transición, las declaraciones condicionadas en Excel se pueden usar para modelar la probabilidad de que se esté usando un dado cargado. Por favor refiérase al ejemplo dos para la hoja de Excel del modelo oculto de Markov.

Los HHM se pueden modelar usando Matlab. Siga el enlace al sitio que contiene información sobre la instalación de la caja de herramientas HHM en Matlab:

HHM en Matlab

Ejemplo$\PageIndex{1}$: "What should I wear?"

El clima afecta temas importantes como, elección de ropa, zapatos, lavarse el cabello, y muchos más. Considerando el extraño clima en Ann Arbor, se desea poder calcular la probabilidad de que llueva dados los datos de los últimos tres días consecutivos. Aplicando tus habilidades de ingeniería química y empoderado por el conocimiento de este artículo de Wiki, te sientas y decides ser la próxima Persona del Tiempo.

Conoces la siguiente información ya que eres un ávido fanático del Canal del Tiempo desde los 5 años.

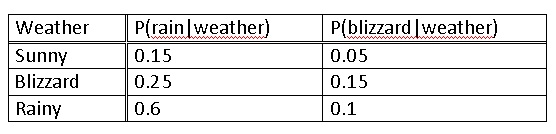
EatherTable 1updated.JPG

Después se registra el clima de los últimos 3 días.

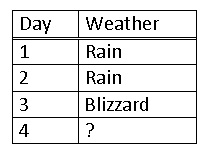
Solución

Como el último día fue una ventisca usas una matriz que expresaba un 100% de probabilidad en el pasado, y multiplicas esto por las probabilidades de cada tipo de clima.

\ [\ left [\ begin {array} {lll}
0 & 1 & 1
\ end {array}\ right]\ left [\ begin {array} {ccc}
8 & 15 & 05\\
.6 & 25 & .15\\
3 & .6 & .1
\ end {array}\ right] =\ left [\ begin {array} {lll}
.6 & .25 y .15
\ end {array}\ derecha]\ nonumber\]

Esto significa que hay un 60% de probabilidad de sol, un 25% de probabilidad de lluvia y un 15% de probabilidad de ventisca. Esto se debe a que un proceso de Markov funciona en base a la probabilidad del evento inmediatamente anterior. Así, decides que es un riesgo lo suficientemente bajo y felizmente decides lucir tu mejor atuendo nuevo Y lavarte el cabello.

Ejemplo$\PageIndex{2}$: "What should I wear for the weekend?"

Resulta que al día siguiente llueve y te empapa tu ropa favorita. No obstante, te vas por un fin de semana con tu familia y debes decidir qué ponerte para los próximos dos días. ¿Cuál es la predicción para los próximos dos días?

Solución

Predecir para el primer día es como el ejemplo anterior sustituyendo la lluvia por una ventisca.

\ [\ left [\ begin {array} {lll}
0 & 0 & 1
\ end {array}\ right]\ left [\ begin {array} {ccc} {ccc}
.8 & .15 & .05\\
.6 & .25 & .15\
.3 & .6 & .1
\ end {array}\ right] =\ left [\ begin {array} {lll}
.3 & amp; .6 & .1
\ end {array}\ derecha]\ nonumber\]

Para predecir para el segundo día debemos usar nuestros datos previos para predecir cómo actuará el clima. Como pronosticamos dos días por delante multiplicamos las probabilidades dos veces, efectivamente cuadrándolas.

\ [\ left [\ begin {array} {lll}
0 & 0 & 1
\ end {array}\ right]\ left [\ begin {array} {lll}
8 & 15 & 05\\
6 & 25 & .15\\
3 & 6 & .1
\ end {array}\ right] ^ {2} =\ left [\ begin {array} {llll}
.63 & amp; .255 & .115
\ end {array}\ derecha]\ nonumber\]

Alternativamente, podemos tomar la predicción del día anterior y multiplicarla por la probabilidad de clima.

\ [\ begin {array} {lllll}
\ text {L.} 3 & .6 & 1\ rfloor & .0 & .15 & .05\\
.6 & .25 & .15 & =.63 & .255 & .115
\ end {array}\ nonumber\]

Ambas formas te dan la misma respuesta. Por lo tanto, decides empacar tanto para clima soleado como lluvioso.

Ejemplo$\PageIndex{3}$: OSEH Example

Ahora, volviendo a las aplicaciones de ingeniería química REAL, las teorías de probabilidad descritas anteriormente pueden usarse para verificar si un equipo está funcionando. Por ejemplo, eres inspector de OSEH y tienes que analizar un conjunto de datos que registran los niveles de contaminantes de una planta. Si usan el depurador que tienen, la probabilidad de que los niveles de contaminantes sean altos es baja. Sin embargo, si no se utiliza el depurador, aumenta la probabilidad de que los niveles de contaminantes sean altos. Ha obtenido alguna información privilegiada de que los operadores usan los depuradores solo 70% de descuento en el tiempo. Tu tarea es crear un modelo basado en las grabaciones de datos y usando teorías de probabilidad para predecir CUÁNDO cambian sus depuradores ON y OFF, para que puedas atraparlos con las manos en la masa en el acto!

Hay 6 posibles niveles de contaminantes: ninguno, bajo, medio-bajo, med, med-alto y alto. Si el nivel = alto, entonces esto está por encima del límite permitido. Todos los demás niveles se consideran permisibles. Si el depurador está ENCENDIDO, existe la misma posibilidad de que ocurra alguno de los estados. Si el depurador está APAGADO, hay un 50% de probabilidad de que se registre un alto nivel de contaminante.

Dados los siguientes datos:

Solución

Las fórmulas utilizadas se enumeran a continuación:

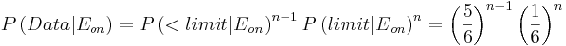
(1) $\ left (Datos|E_ {on}\ right) =P\ left (<limit|E_ {on}\ right) ^ {n-1} P\ left (límit|E_ {on}\ right) ^ {n} =\ left (\ frac {5} {6}\ right) ^ {n-1}\ left (\ frac {1} {6}\ right) ^ {n}$

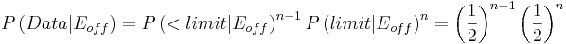
(2) $\ left (Datos|E_ {off}\ right) =P\ left (<limit|E_ {off}\ right) ^ {n-1} P\ left (límit|E_ {off}\ right) ^ {n} =\ left (\ frac {1} {2}\ right) ^ {n-1}\ left (\ frac {1} {2}\ right) ^ {n}$

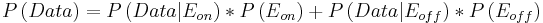
(3) $\ left (Data\ right) =P\ left (Datos|E_ {on}\ right) *P\ left (E_ {on}\ right) +P\ left (Datos|E_ {off}\ right) *P\ left (E_ {off}\ right)$

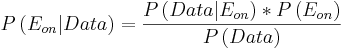
(4) $\ left (E_ {on} |Data\ right) =\ frac {P\ left (Datos|E_ {on}\ right) *P\ left (E_ {on}\ right)} {P\ left (Data\ right)}$

Consulte el archivo Excel adjunto para conocer el modelo predictivo. OSEHEjemplo

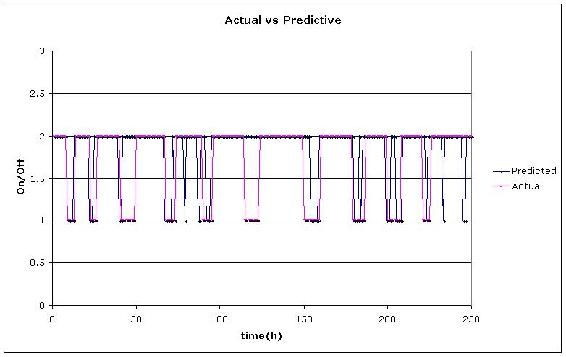
A partir de nuestros resultados en el archivo Excel, graficamos los tiempos predichos vs reales cuando se apagó el depurador. El valor de “1" se eligió arbitrariamente para representar cuando el depurador estaba APAGADO y “2" cuando estaba “ON”.

Pregunta de opción múltiple 1

¿Cuál es la propiedad clave de una cadena de Markov?

A) La probabilidad de cada símbolo depende de los símbolos FUTUROS.

B) La probabilidad de cada símbolo depende de TODOS los símbolos anteriores.

C) La probabilidad de cada símbolo depende de NINGUNO de los símbolos anteriores.

D) La probabilidad de cada símbolo depende únicamente del valor del símbolo ANTERIOR.

Pregunta de opción múltiple 2

¿Qué tipo de parámetros representa la probabilidad de emisión?

A) parámetros desconocidos

B) Parámetros de Markov

C) parámetros conocidos

D) Parámetros de Bayes

Referencias

Woolf P., Keating A., Burge C., y Michael Y. “Imprimación de Estadística y Probabilidad para Biólogos Computacionales”. Instituto Tecnológico de Massachusetts, BE 490/ Bio7.91, primavera de 2004
Smith W. y Gonic L. “Cartoon Guide to Statistics”. Harper Perennial, 1993.
Kemeny J., Snell J. “Cadenas finitas de Markov”. Springer, 1976. ISBN 0387901922
es.wikipedia.org/wiki/Serpientes y Escaleras
Page, Lawrence; Brin, Sergey; Motwani, Rajeev y Winograd, Terry (1999). “El ranking de citas PageRank: Trayendo orden a la Web”

Utilice el estilo Harvard References para las referencias en el documento.
Para más información sobre cuándo hacer referencia consulta la siguiente entrada de Wikipedia.
Ross, Sheldon M. “Introducción a los Modelos de Probabilidad”. Prensa Académica, 2007.

Colaboradores

Autores: Nicole Blan, Jessica Nunn, Pamela Roxas, Cynthia Sequerah
Administradores: Kyle Goszyk, So Hyun Ahn, Sam Seo, Mike Peters

Search

Ejemplo\(\PageIndex{1}\): Will It Rain Tomorrow?

Ejemplo\(\PageIndex{1}\): Queuing Problem

Ejemplo\(\PageIndex{1}\): "What should I wear?"

Ejemplo\(\PageIndex{2}\): "What should I wear for the weekend?"

Ejemplo\(\PageIndex{3}\): OSEH Example