13.8: Distribuciones continuas- normales y exponenciales

Autores: Navin Raj Bora, Dallas Burkholder, Nina Mohan, Sarah Tschirhart

Introducción

Se dice que las variables aleatorias cuyos espacios no están compuestos por un número contable de puntos sino que son intervalos o una unión de intervalos son del tipo continuo. Las distribuciones continuas son modelos de probabilidad utilizados para describir variables que no ocurren en intervalos discretos, o cuando un tamaño de muestra es demasiado grande para tratar cada evento individual de manera discreta (consulte Distribuciones Discretas para obtener más detalles sobre distribuciones discretas). La principal diferencia entre las distribuciones continuas y discretas es que las distribuciones continuas tratan con un tamaño de muestra tan grande que sus valores de variables aleatorias se tratan en un continuo (de infinito negativo a infinito positivo), mientras que las distribuciones discretas tratan con poblaciones de muestra más pequeñas y por lo tanto no pueden ser tratados como si estuvieran en un continuo. Esto lleva a una diferencia en los métodos utilizados para analizar estos dos tipos de distribuciones: las distribuciones continuas y discretas es las distribuciones continuas se analizan mediante cálculo, mientras que las distribuciones discretas se analizan mediante aritmética. Hay muchos tipos diferentes de distribuciones continuas, incluidas algunas como Beta, Cauchy, Log, Pareto y Weibull. En este wiki, sin embargo, solo cubriremos los dos tipos más relevantes de distribuciones continuas para ingenieros químicos: distribuciones normales (gaussianas) y distribuciones exponenciales.

En ingeniería química, el análisis de distribuciones continuas se utiliza en una serie de aplicaciones. Por ejemplo, en el análisis de errores, dado un conjunto de datos o función de distribución, es posible estimar la probabilidad de que una medición (temperatura, presión, caudal) caiga dentro de un rango deseado, y de ahí determinar qué tan confiable es un instrumento o pieza de equipo. Además, se puede calibrar un instrumento (por ejemplo, sensor de temperatura) del fabricante de forma regular y usar una función de distribución para ver la varianza en los aumentos o disminuciones de las mediciones de los instrumentos con el tiempo.

Distribuciones Normales

¿Qué es una curva de distribución gaussiana (normal)?

Una distribución gaussiana se puede utilizar para modelar el error en un sistema donde el error es causado por eventos relativamente pequeños y no relacionados.

Esta distribución es una curva que es simétrica respecto a la media (es decir, una curva en forma de campana) y tiene un rango medido por desviaciones estándar por encima y por debajo de la media del conjunto de datos (consulte Estadísticas Básicas para una discusión adicional sobre estos parámetros estadísticos). Para explicar mejor, considere que un cierto porcentaje de todos los puntos de datos caerá dentro de una desviación estándar de la media. De igual manera, más puntos de datos caerán dentro de dos desviaciones estándar de la media, y así sucesivamente. Sin embargo, bajo este modelo requeriría un rango infinito para capturar TODOS los puntos de datos presentando así una dificultad menor en este appraoch.

La siguiente figura es una posible distribución gaussiana, donde la media (μ) es 10 y la desviación estándar (σ) es 2. F (x) es el número de veces que un cierto valor de x ocurre en la población. La media es simplemente el promedio numérico de todas las muestras de la población, y la desviación estándar es la medida de qué tan lejos de la media tienden a desviarse las muestras. En las siguientes secciones se explica cómo y por qué se usa una curva de distribución normal en el control y qué significa sobre conjuntos de datos.

Figura 1: Curva genérica de distribución normal

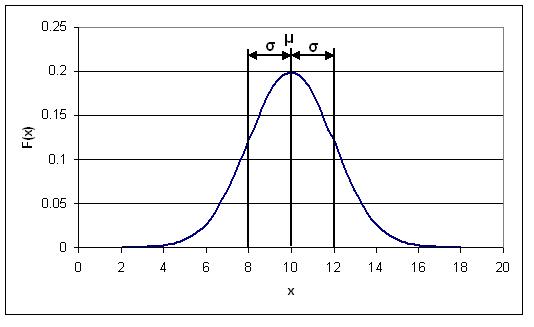
La función de densidad de probabilidad (PDF) para una distribución normal

Como se mencionó en la sección Introducción, las curvas de distribución pueden ser utilizadas para determinar la probabilidad, P (x), de que ocurra un determinado evento. Cuando esto se hace, la curva de distribución se conoce como Función de Densidad de Probabilidad (PDF). En la figura mostrada anteriormente, el eje x representa el rango de posibles eventos (por ejemplo, el rango de edades en una población de muestra o la magnitud del ruido generado por un sensor de temperatura). El eje y representa el número de veces que un cierto valor x ocurre en una población. El PDF se puede describir matemáticamente de la siguiente manera:

En algunos casos, puede que no sea necesario conocer la probabilidad de que ocurra un solo evento. Más bien, es posible que desee conocer la probabilidad de un rango de eventos (por ejemplo, ¿cuál es la probabilidad de que el ruido generado por mi sensor de temperatura caiga en el rango de 5-10 Hz?). Cuando esto suceda, deberá integrar el PDF anterior sobre el rango deseado, de la siguiente manera:

donde k ₁ y k ₂ son los límites de su rango deseado. Esta integral da como resultado la siguiente expresión:

La función Erf se puede encontrar en la mayoría de las calculadoras científicas y también se puede calcular usando tablas de valores de Erf []. Por ejemplo, su uso aquí es paralelo a lo que aprendimos en ChE 342, Transferencia de Calor y Masa. Determine el valor dentro de los corchetes de la función erf mediante aritmética simple, luego tome este valor y encuentre el número Erf correspondiente de una tabla. Finalmente utilizar este valor en el cálculo para determinar la probabilidad de que un determinado punto, x, caiga dentro de un rango limitado de k1 a k2.

Cálculo de Muestras

Dado un conjunto de datos con un promedio de 20 y una desviación estándar de 2, ¿cuál es la probabilidad de que un punto de datos seleccionado aleatoriamente caiga entre 20 y 23?

Solución 1

Para resolver simplemente sustituya los valores en la ecuación anterior. Esto produce la siguiente ecuación:

Estos valores de Erf deben buscarse en una tabla y sustituirse en la ecuación. Haciendo esto yeilds

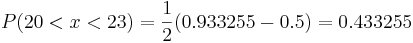
Así, existe una probabilidad de 43.3255% de seleccionar aleatoriamente un número del conjunto de datos con un valor entre 20 y 23.

Gráficamente hablando, el PDF es solo el área bajo la curva de distribución normal entre k ₁ y k ₂. Entonces, para la distribución que se muestra arriba, el PDF para 8<x<12 correspondería al área de la región sombreada naranja en la siguiente figura:

Figura 2: PDF para 8<x<12

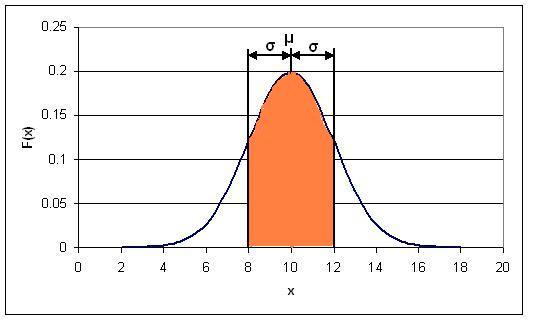
Solución 2

Alternativamente, en lugar de usar la función de error, la función de densidad de probabilidad incorporada de Mathematica se puede usar para resolver este problema. Esta función de densidad de probabilidad se puede aplicar a la distribución normal usando la sintaxis que se muestra a continuación.

nIntegrar [PDF [NormalDistribution [μ, σ], x], {x, x1, x2}]

En esta sintaxis, μ representa la media de la distribución, σ representa la desviación estándar de la distribución, y x1 y x2 representan los límites del rango.

Esta función se puede aplicar a este problema como se muestra a continuación.

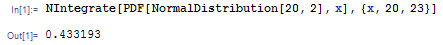
Esto muestra que la probabilidad de que un punto de datos seleccionado al azar caiga entre 20 y 23 es de 0.4332, o 43.32%. Como era de esperar, este valor calculado usando la función de densidad de probabilidad incorporada en Mathematica coincide con el valor calculado a partir del uso de la función de error. Mathematica proporciona una solución más rápida a este problema.

Un punto importante a tener en cuenta sobre el PDF es que cuando se integra del infinito negativo al infinito positivo, la integral siempre será igual a uno, independientemente de la media y desviación estándar del conjunto de datos. Esto implica que hay un 100% de probabilidad de que tu variable aleatoria x caiga entre el infinito negativo y el infinito positivo. Asimismo, la integral entre el infinito negativo y la media es 0.5, o existe un 50% de probabilidad de encontrar un valor en esta región debido a la naturaleza simétrica de la distribución.

La función de densidad acumulativa (CDF) para una distribución normal

Para hacer la transición de nuestra argumentación a una perspectiva más holística con respecto a la función de densidad de probabilidad para una distribución normal, presentamos la función de densidad acumulativa, que representa la integral (área bajo la curva) del PDF desde el infinito negativo hasta algún valor dado en el eje y de la gráfica incrementalmente de acuerdo con el eje x, que sigue siendo el mismo que antes. Debido a este tipo de definición, podemos eludir el riguroso análisis de la función de error presentado anteriormente simplemente restando un punto CDF de otro. Por ejemplo, si los ingenieros desean determinar la probabilidad de que un cierto valor de x caiga dentro del rango definido por k1 a k2 y poseen un gráfico con datos de la CDF relevante, simplemente pueden encontrar CDF (k2) - CDF (k1) para encontrar la probabilidad relevante.

La Función de Densidad Acumulativa (CDF) es simplemente la probabilidad de que la variable aleatoria, x, caiga en o por debajo de un valor dado. Por ejemplo, este tipo de función se utilizaría si quisieras saber la probabilidad de que el ruido de tu sensor de temperatura sea menor o igual a 5 Hz. El CDF para una distribución normal se describe usando la siguiente expresión:

donde k es el valor máximo permitido para x.

La principal diferencia entre el PDF y el CDF es que el PDF da la probabilidad de que tu variable x caiga dentro de un rango definido, donde el CDF da la probabilidad de que tu variable x caiga en o por debajo de un cierto límite, k La siguiente figura es la CDF para una distribución normal. Notarás que a medida que x se acerca al infinito, el CDF se acerca a 1. Esto implica que la probabilidad de que x caiga entre infinito negativo y positivo es igual a 1.

Figura 3: Gráfica de CDF para una Distribución Normal

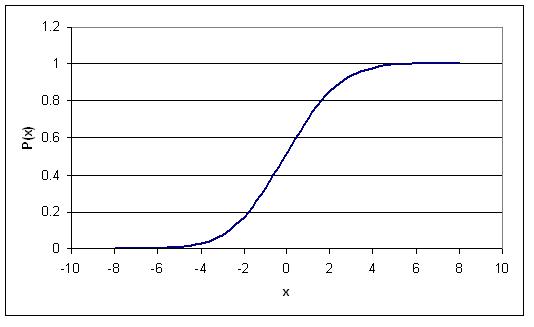
Distribución Normal Estándar

Un tipo especial de curva de distribución de probabilidad se denomina Distribución Normal Estándar, que tiene una media (μ) igual a 0 y una desviación estándar (σ) igual a 1.

Este modelo simplificado de distribución generalmente ayuda a ingenieros, estadísticos, estrategas de negocios, economistas y otros profesionales interesados a modelar las condiciones del proceso y asociar la atención y el tiempo necesarios para abordar problemas particulares (es decir, mayor probabilidad de que una condición fallida requiera atención adicional, etc.). Además, nuestras calificaciones en muchos de los cursos aquí en la U de M, tanto dentro como fuera del colegio de ingeniería, se basan estricta o vagamente fuera de este tipo de distribución. Por ejemplo, el rango B normalmente se encuentra dentro de +/- de una desviación estándar.

La siguiente figura es una curva de Distribución Normal Estándar:

Figura 4: Curva de distribución normal estándar

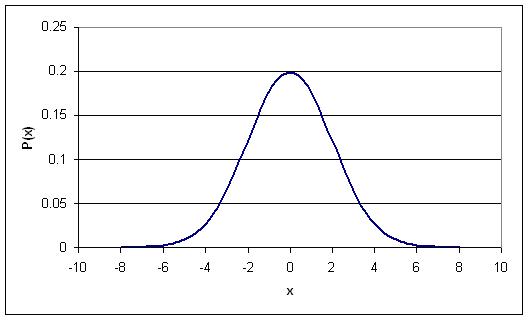
El beneficio de la distribución normal estándar es que se puede utilizar en lugar de la función Erf [], si no se tiene acceso a una calculadora científica o tablas Erf []. Para utilizar la curva de Distribución Normal Estándar, se debe seguir el siguiente procedimiento:

1.Realizar una transformación z. Se trata de una transformación que normaliza esencialmente cualquier distribución normal en una distribución normal estándar. Se realiza utilizando la siguiente relación:

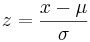
Matemáticamente hablando, la transformada z normaliza los datos cambiando todos los puntos de datos brutos en puntos de datos que dictan cuántas desviaciones estándar se alejan de la media. Entonces, independientemente de la magnitud de los puntos de datos brutos, la estandarización permite comparar múltiples conjuntos de datos entre sí.

2.Utilice una tabla normal estándar para encontrar el valor p. Una tabla normal estándar tiene valores para z y valores correspondientes para F (x), donde F (x) se conoce como el valor p y es solo la probabilidad acumulativa de obtener un valor x particular (como un CDF). Una tabla normal estándar puede parecerse a la siguiente tabla (cabe señalar que si se trata de una Tabla Normal Estándar que contiene solo valores z positivos, se puede usar la siguiente propiedad para convertir sus valores z negativos en positivos: F (-z) =1-F (z)):

Tabla 1: Mesa Normal Estándar

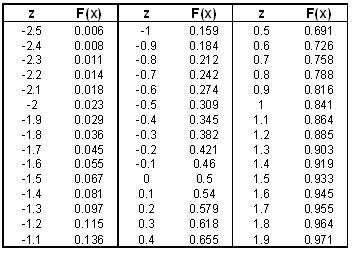
Una tabla normal estándar más detallada se puede encontrar aquí (Nota: Esta tabla es la misma tabla utilizada en el wiki de 'Estadísticas Básicas').

3. ¿Y si quiero que la probabilidad de que z caiga entre un rango de x=a y x=b?. Primero, encuentra tus dos valores z que corresponden a a y b. Entonces estos serían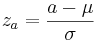 y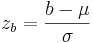, respectivamente. La probabilidad de que x caiga entre a y b es justamente: F (zb) — F (za), donde F (zb) y F (za) se encuentran a partir de las tablas normales estándar.

Cálculo de Muestras

Tomemos el mismo escenario que se utilizó anteriormente, donde se tiene un conjunto de datos con un promedio de 20 y desviación estándar de 3 y calculemos la probabilidad de que un punto de datos seleccionado aleatoriamente esté entre 20 y 23.

Solución

Para ello basta con restar las dos puntuaciones Z:

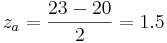
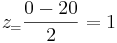
Estas puntuaciones Z corresponden a probabilidades de 0.933 y 0.5 respectivamente. Su diferencia, 0.433, es la probabilidad de que un valor seleccionado al azar caiga entre los dos. Observe que esto es casi idéntico a la respuesta obtenida usando el método Erf. Tenga en cuenta que obtener esta respuesta también requirió mucho menos esfuerzo. Esta es la principal ventaja de usar puntajes Z.

Propiedades de una Distribución Normal

Existen varias propiedades para distribuciones normales que se vuelven útiles en las transformaciones.

1 Si X es una normal con media μ y σ ² a menudo anotada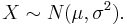 entonces la transformación de un conjunto de datos a la forma de aX + b sigue a.

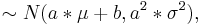2 Se puede utilizar una distribución normal para aproximar una distribución binomial (n ensayos con probabilidad p de éxito) con parámetros μ = np y σ ² = np (1 − p). Esto se deriva utilizando los resultados limitantes del teorema del límite central.

3 Se puede utilizar una distribución normal para aproximar una distribución de Poisson (parámetro λ) con parámetros μ = σ ² = λ. Esto se deriva utilizando el teorema del límite central.

4 La suma a de variables aleatorias siguiendo la misma distribución normal ~ N (n μ, n σ ²). Este resultado muestra la media de la muestra.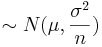

5 El cuadrado de una variable normal estándar es una variable chi-cuadrada con un grado de libertad.

6 Combinando 4 y 5 arroja la suma de n variables normales estándar cuadradas es una variable chi-cuadrada con n grados de libertad. Esto tiene aplicación para pruebas de chi-cuadrado como se ve en otras secciones de este texto.

Distribución Exponencial

La distribución exponencial puede pensarse como una versión continua de la distribución geométrica sin memoria alguna. A menudo se utiliza para modelar el tiempo para que un proceso ocurra a una tasa promedio constante. Los eventos que ocurren con una probabilidad conocida para un valor x dado construyen la teoría desarrollada previamente (es decir, F (x) vs. X, F (x) en este caso es diferente a la anterior), donde x puede indicar la distancia entre mutaciones en una cadena de ADN., por un ejemplo aplicación, tasa de falla del instrumento, o tiempo requerido para un partículas radiactivas a desintegración (la RATE de desintegración) para las siguientes aplicaciones.

Sin embargo, recuerde que la suposición de una tasa constante rara vez se mantiene como válida en la actualidad. La tasa de llamadas telefónicas entrantes difiere según la hora del día. Pero si nos enfocamos en un intervalo de tiempo durante el cual la tarifa es aproximadamente constante, como de 2 a 4 p.m. durante los días laborales, la distribución exponencial se puede utilizar como un buen modelo aproximado para el tiempo hasta que llegue la siguiente llamada telefónica.

Se puede implementar la función de distribución exponencial en Mathematica usando el comando: ExponentialDistribution [lambda].

O, para una comprensión más popular de la función, consulte el siguiente sitio web, detallando el número de tiburones vistos en el área de una milla cuadrada en diferentes períodos de tiempo de una hora. Usa el botón “Pez” para ejecutar el applet. Para cambiar el parámetro lambda, escriba el valor y presione el botón “Borrar”.

www.math.csusb.edu/facultación/stanton/m262/poisson_distribution/poisson_old.html

La función de densidad de probabilidad (PDF)

Algunas notas son dignas de mención a la hora de diferenciar el PDF de la función Distribución exponencial de dos parámetros. A medida que λ disminuye en valor, la distribución se estira hacia la derecha, y a medida que λ se incrementa, la distribución se empuja hacia el origen. Esta distribución no tiene parámetro de forma ya que tiene una sola forma, es decir, la exponencial, y el único parámetro que tiene es la tasa de fallas, λ. La distribución comienza en T = 0 al nivel de f (T = 0) = λ y disminuye a partir de entonces exponencial y monótonamente a medida que T aumenta, y es convexa. El PDF para una distribución exponencial se da en el siguiente formulario, donde λ es el parámetro de tasa y x es variable aleatoria:

Figura 5: PDF (λ = 0.25) para Distribución Exponencial

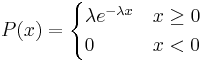
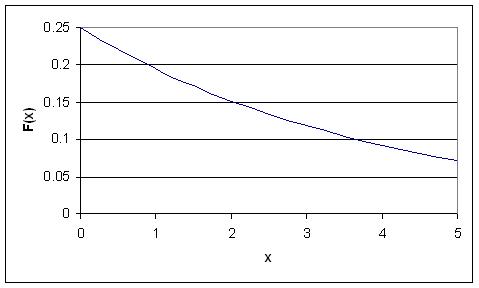
Aquí, x podría representar el tiempo mientras que el parámetro de tasa podría ser la velocidad en la que se produce la disminución. El parámetro de tasa debe ser constante y mayor que 0. El PDF disminuye continuamente en este diagrama debido a su definición como ejemplo de decaimiento. La desintegración exponencial típicamente modela partículas radiactivas que pierden masa por unidad de tiempo. Así F (x) representa la masa de la partícula con x igualando el tiempo transcurrido desde el inicio de la descomposición. A medida que pasa el tiempo, la masa cae debido a la desintegración radiactiva (la partícula emite radiación como forma de liberación de energía, cualquier energía que resulte resta de la masa, E = MC ²).

La función de distribución acumulativa (CDF)

El CDF para una distribución exponencial se expresa usando lo siguiente:

Figura 6: CDF (λ = 1) para distribución exponencial

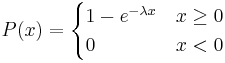
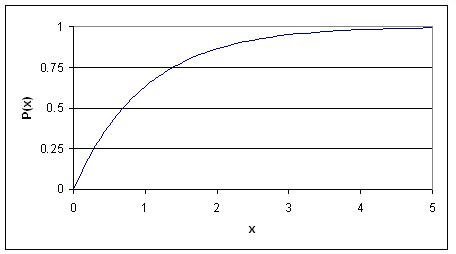
Siguiendo el ejemplo dado anteriormente, esta gráfica describe la probabilidad de que la partícula se desintegre en una cierta cantidad de tiempo (x).

Propiedades de la Distribución Exponencial

Entre las funciones de distribución, la función de distribución exponencial tiene dos propiedades únicas, son la propiedad sin memoria y una tasa de riesgo constante.

— La propiedad sin memoria —

Si una variable aleatoria, X, sobrevivió por “t” unidades de tiempo, entonces la probabilidad de que X sobreviva a una “s” unidades de tiempo adicionales es la misma que la probabilidad de que X supere “s” unidades de tiempo. La variable aleatoria ha “olvidado” que ha sobrevivido por “t” unidades de tiempo, por lo que esta propiedad se llama la propiedad “sin memoria”.

Una variable aleatoria, X, no tiene memoria si

P {X > s+t | X > t} = P {X > s} para todas las s, t (1)

A partir del uso (1) anterior y la definición de probabilidad condicional:

s, X > t)} {P (X > t)} = P (x > s)” src=”/@api /deki/files/19503/image-794.png “> (2)

y así:

P {X > s+t} = P {X > s} P {X > t} (3)

para probar la propiedad anterior, suponemos que existe una función tal que F (x) =P {X > x}.

por la ecuación 3 anterior, tenemos

F (x+t) = F (s) F (t) (4)

Por cálculo elemental, la única solución continua para este tipo de funcionamientouna ecuación es

F (x) = e ^{− λ x} (5)

Así se demuestra que la única distribución que puede resolver la ecuación (4), o la propiedad sin memoria, es una función exponencial.

— La Propiedad de Tasa de Peligro Constante —

Supongamos que la variable aleatoria, X, sobrevivió por “t” unidades de tiempo, y r (t) representa la probabilidad condicional de que la variable t-años falle. Matemáticamente, la tasa de riesgo, o la tasa de fallas, se define como:

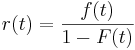(6)

Para la distribución exponencial, la tasa de riesgo es constante ya que

f (t) = e ^{− λ x},

y

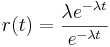
r (t) = λ

lo anterior demostró que r (t) es constante para la distribución exponencial.

Distribución Exponencial Estándar

Cuando una distribución exponencial tiene λ = 1, esto se denomina distribución exponencial estándar. La ecuación y la figura para esta función se describen a continuación:

Figura 7: Curva de distribución exponencial estándar

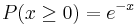
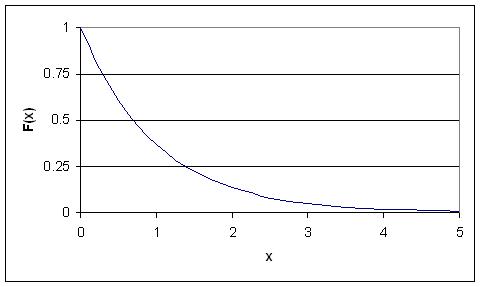
Este tipo de distribución es una forma de estandarizar tu gráfica. Esto es paralelo a nuestro ejemplo anterior de distribución normal estándar, sin embargo, dado que el tiempo es ahora la variable x, puede que no sea negativa (como suposición de nuestro hipotético escenario). Así, la desintegración ocurre solo por tiempo positivo (ya que la partícula radiactiva emite masa).

Funcionado Ejemplo 1

Usted es el ingeniero de procesos líder de una compañía farmacéutica líder, y su responsabilidad más reciente es caracterizar uno de sus biorreactores. Parte de esta caracterización es determinar la varianza de temperatura dentro del reactor durante la última etapa en una reacción isotérmica. Después de tomar datos durante esta reacción durante dos semanas seguidas, se determina que la temperatura promedio de la reacción es de 30 C, siendo una desviación estándar de su conjunto de datos de 3 C. Además, los datos se ajustan a una distribución normal (es decir, no está sesgada a ninguno de los lados de la media) Los más altos, es decir, los que darte las subidas, decide que este reactor necesita operar dentro de los 6 grados de su temperatura media de operación al menos 60% del tiempo. Dados los datos que has tomado, ¿el reactor cumple con estos estándares, o vas a estar tirando unas 80 horas semanas en un futuro próximo tratando de arreglar el proceso?

Solución

La información que se da en este problema es la siguiente:

• Promedio: 30
• Desviación estándar: 3
• Queremos encontrar la probabilidad de que la temperatura caiga entre 24 y 36 C

Usando el PDF para una Distribución Normal, podemos decir que:

Esta expresión se puede resolver fácilmente usando una tabla de valores Erf [] así como la propiedad de la función Erf que establece Erf (-x) =-Erf (x). Otro enfoque sencillo sería usar Mathematica con la sintaxis que se muestra a continuación.

Resolviendo para P (24<T<36), obtenemos que la probabilidad de que la temperatura caiga dentro de dos desviaciones estándar del promedio sea de aproximadamente 95% Dado que este valor es mucho mayor que el 60% requerido, puede estar seguro de que su reactor está funcionando bien.

Funcionado Ejemplo 2

Eres ingeniero en una planta que produce un combustible volátil. En su primera semana en el trabajo tanto el control primario como el control de redundancia fallan en el mismo día, requiriendo el importante inconveniente de apagar el reactor para evitar una explosión mucho más inconveniente. Tu jefe quiere que decidas si simplemente reemplazar ambos sensores o agregar un sensor adicional para asegurar que tales problemas se eviten en el futuro. Si bien agregar otro sensor ciertamente ayudaría a resolver el problema hay un costo adicional asociado con la compra e instalación del sensor. Un compañero ingeniero muy útil con una inclinación por las estadísticas te ayuda informándote que estas fallas de doble instrumento ocurren a razón de uno por 3.8 * 10 ⁸ horas. ¿Cuál es la probabilidad de que este tipo de fallas vuelva a ocurrir en los próximos 50 años (la vida estimada de la planta)? ¿Cuál es su recomendación a su jefe?

Solución

Porque se le da la probabilidad de que ocurra el evento y está interesado en la cantidad de tiempo que separa dos eventos usando una distribución exponencial es apropiado. Para resolver esto, usa la expresión CDF:

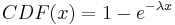
En este caso λ se da en horas y x en años, por lo que primero debes convertir una de las unidades. También la tasa da está en eventos por hora. λ debe ingresarse en la ecuación como la inversa (probabilidad por unidad de tiempo). Ingresando los números apropiados yeilds la siguiente ecuación:

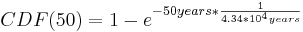
Existe una probabilidad de 0.115% de que ambos sensores fallen en el mismo día en algún momento de los próximos 50 años. Con base en estos datos se puede concluir que probablemente esté seguro simplemente reemplazando los dos sensores y no agregando un tercero.

Ejemplo 3

Trabajas en una planta química que utiliza la famosa reacción A + B -> C para producir C. Como parte de tu proceso, operas un tanque de mezcla para diluir el reactivo A antes de enviarlo al reactor. El reactivo B es un subproducto de otro proceso en la planta y entra a una tasa variable. Esto provoca fluctuaciones en el nivel del tanque de mezcla para el reactivo A ya que el flujo de entrada y salida del tanque tiene que ser ajustado. En el pasado esto ha provocado desbordamientos en el tanque de mezcla A que tu jefe te ha encargado evitar. Usted ha decidido que la forma más fácil de evitar desbordamientos es simplemente comprar un tanque de mezcla más grande. Actualmente el tanque de mezcla es de 50 galones. Después de algunos experimentos se encuentra que las condiciones normales de funcionamiento del tanque son 45 galones de reactivo A con una desviación estándar de 3 galones. Sin embargo, para minimizar los costos, el tanque debe ser lo más pequeño posible. ¿Cuál es el tanque más pequeño que puedes comprar que evita desbordamientos 99.99% de las veces?

Solución:

Valores conocidos:
μ = 45 gal.
σ = 3 gal.

Usando una tabla z se encuentra que el valor z más pequeño que da una F (x) de 0.9999 es 3.71. Luego reorganizas la ecuación z que se da a continuación para resolver x y enchufar todos los valores conocidos.

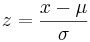
x = z * σ + μ

x = 3.71 * 3 + 45 = 56.1

Para evitar desbordamientos 99.99% de las veces el tanque más pequeño que se puede utilizar es 56.1 gal.

Pregunta de opción múltiple 1

Resuma brevemente la diferencia principal entre distribuciones continuas y discretas, y sus respectivos métodos de análisis:

a. Las distribuciones continuas y las distribuciones discretas siempre se analizan a través de métodos de cálculo únicamente. Las distribuciones continuas son distintas de las distribuciones discretas en que el tamaño de la muestra es demasiado pequeño para tratar cada evento individual de manera discreta.

b. Las distribuciones continuas se analizan aplicando métodos de cálculo, mientras que las distribuciones discretas se abordan comúnmente a través de métodos aritméticos. Las distribuciones continuas son distintas de las distribuciones discretas en que el tamaño de la muestra es demasiado grande para tratar cada evento individual de manera discreta.

c. Al realizar una transformada z- estándar, el estudiante interesado puede iniciar el proceso de caracterización de la probabilidad de que z caiga entre el rango específico de x = 'a' y x = 'b'.

d. Las funciones de error nos permiten determinar la probabilidad de que un punto de datos se encuentre dentro de ciertos límites sin tener que completar el riguroso de la función de distribución de probabilidad. Las distribuciones continuas pueden abordarse de esta manera ya que su tamaño de muestra es demasiado confuso para ser abordado de manera discreta.

Pregunta de opción múltiple 2

Explique la diferencia filosófica primaria entre los parámetros de la función de distribución de probabilidad (PDF) y la función de distribución acumulativa (CDF).

a. ¿Quién usa la palabra filosófico en un problema de ingeniería química? Lo más probable es que el autor de esta pregunta esté confundido y se esfuerce demasiado, por lo que voy a protestar al no responder.

b. El PDF y el CDF son idénticos en aplicación, y como tales, también deben tener parámetros idénticos.

c. El PDF y el CDF miden comúnmente la probabilidad de que el ruido del sensor esté en o por debajo de un valor específico. Son diferentes en el hecho de que el CDF contiene un rango específico de uso, que va de k1 a k2, mientras que el PDF no, ya que sube del infinito negativo a un valor, k.

d. La mayor diferencia entre el PDF y el CDF es que el PDF proporciona la probabilidad de que la variable x se encuentre dentro de un rango definido. Alternativamente, CDF da la probabilidad de que la variable x caiga en o por debajo de un cierto límite, k.

Rincón de Sage

Producción de Insulina Terapéutica
www.youtube.com/V/B3ADQDoZP5i

Un breve problema sobre las funciones de distribución exponencial continua
video.google.com/googleplayer... 13000402551106

Una copia de las diapositivas se puede encontrar aquí:Diapositivas sin narración

Funciones de Distribución Normal en Excel

Si YouTube no funciona, haga clic aquí Funciones normales de distribución en Excel

Referencias

• Gernie, L. y W. Smith “Cartoon Guide to Statistics” Harper Perennial, c. 1993