10.4: Colisiones bidimensionales de partículas
- Page ID
- 83943
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Para analizar colisiones en dos dimensiones, necesitaremos adaptar los métodos que utilizamos para una sola dimensión. Para comenzar, la ecuación de conservación del impulso seguirá aplicándose a cualquier tipo de colisión.
\[ m_A \ \vec{v}_{A,f} + m_B \ \vec{v}_{B,f} = m_A \ \vec{v}_{A,i} + m_B \ \vec{v}_{B,i} \]
Esto es, por supuesto, una ecuación vectorial, así que podemos romper todas esas velocidades en componentes para convertir nuestra ecuación de un vector en dos ecuaciones escalares. En las ecuaciones siguientes, dividimos la ecuación de conservación de momentum en\(x\) y\(y\) componentes.
\[ m_A \ v_{A,f,x} + m_B \ v_{B,f,x} = m_A \ v_{A,i,x} + m_B \ v_{B,i,x} \]
\[ m_A \ v_{A,f,y} + m_B \ v_{B,f,y} = m_A \ v_{A,i,y} + m_B \ v_{B,i,y} \]
En los subíndices para las velocidades, etiquetamos la partícula (\(A\)o\(B\)), el estado anterior o posterior a la colisión (\(i\)o\(f\)), y el componente (\(x\)o\(y\)). Este triple subíndice puede hacer que las cosas estén un poco abarrotadas, pero siempre y cuando seas metódico sobre etiquetar y leer estos subíndices es bastante sencillo. Para facilitar la interpretación, se recomienda que siga un orden consistente en los subíndices, etiquetando el cuerpo, luego pre/post colisión, luego dirección.
Para complementar la conservación de las ecuaciones de momentum, nuevamente necesitaremos determinar el tipo de colisión, clasificándola como inelástica (donde las dos partículas se pegan después del impacto) o elástica o semielástica (donde las partículas rebotan una de otra).
Colisiones inelásticas:
En el caso de colisiones inelásticas, los cuerpos tendrán la misma velocidad final como consecuencia de pegarse entre sí. Rodando esta relación en las ecuaciones de conservación de momento anteriores, terminamos con las siguientes ecuaciones. Estas ecuaciones modificadas suelen ser suficientes para resolver las incógnitas en las ecuaciones.
\[ m_{(A+B)} \ v_{f,x} = m_A \ v_{A,i,x} + m_B \ v_{B,i,x} \]
\[ m_{(A+B)} \ v_{f,y} = m_A \ v_{A,i,y} + m_B \ v_{B,i,y} \]
Colisiones Elásticas y Semielásticas:
A diferencia de las colisiones inelásticas, las colisiones elásticas y semielásticas tendrán velocidades separadas para cada uno de los cuerpos después de la colisión. Teniendo cada cuerpo separado\(x\) y\(y\) componentes, esto representa cuatro variables desconocidas. Suponiendo que conocemos todas las condiciones de partida, necesitaremos cuatro ecuaciones separadas para resolver todas las incógnitas.
A diferencia de la ecuación de conservación de impulso, la ecuación de conservación de energía que usaríamos para colisiones elásticas no es una ecuación vectorial y no se puede desglosar en componentes. En cambio, tendremos que mirar el coeficiente de restitución, y establecerlo igual a 1 para colisiones elásticas.
Para resolver estos problemas, primero necesitaremos configurar un conjunto específico de ejes de coordenadas. Estos ejes serán la dirección tangencial (a lo largo del plano de la colisión) y la dirección normal (perpendicular al plano de la colisión). Un ejemplo de estas direcciones se muestra en la siguiente figura.
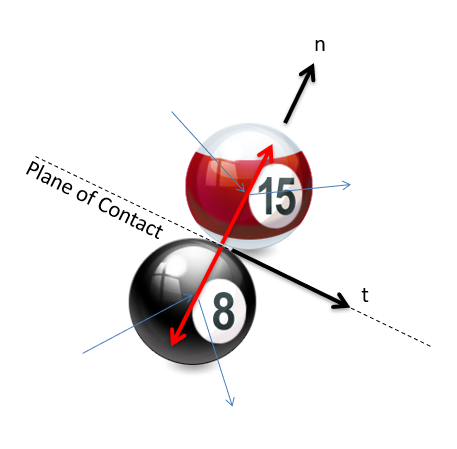
Al examinar la figura anterior, podemos ver algo especial acerca de la dirección tangencial en el sentido de que no hay fuerzas en ninguno de los dos cuerpos en esta dirección. Sin fuerzas, no hay impulso, y sin impulso no hay cambio de impulso para ninguna de las partículas individualmente en la dirección tangencial. Esto significa que la velocidad se conserva para cada cuerpo en la dirección tangencial por sí solo. Sumado a eso, el impulso en su conjunto se conserva en la dirección normal y la ecuación del coeficiente de restitución se puede aplicar a la dirección normal y tenemos las cuatro ecuaciones que necesitamos para resolver la mayoría de los problemas.
\[ v_{A,f,t} = v_{A,i,t} \]
\[ v_{B,f,t} = v_{B,i,t} \]
\[ m_A \ v_{A,f,n} + m_B \ v_{B,f,n} = m_A \ v_{A,i,n} + m_B \ v_{B,i,n} \]
\[ \epsilon = - \frac{v_{A,f,n} - v_{B,f,n}}{v_{A,i,n} + v_{B,i,n}} \]
Para usar las ecuaciones anteriores, necesitaremos desglosar todas las velocidades conocidas en\(n\) y\(t\) componentes, luego simplemente enchufar esos valores y resolver las ecuaciones anteriores. Al final también podemos necesitar convertir los componentes encontrados\(n\) y de\(t\) velocidad en\(x\) y\(y\) componentes o magnitudes y direcciones.
Ejemplo\(\PageIndex{1}\)
Dos autos chocan en una intersección como se muestra a continuación. Los autos se enredan entre sí, pegándose juntos después del impacto. Con base en la información que se da a continuación sobre las velocidades iniciales y suponiendo que ambos autos se deslicen lejos del choque en el ángulo de 30 grados como se muestra, ¿cuál debe haber sido la velocidad inicial del automóvil B antes del impacto?
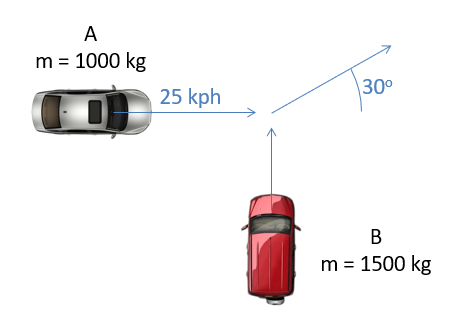
- Solución
-
Video\(\PageIndex{2}\): Solución trabajada a problema de ejemplo\(\PageIndex{1}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/RBegCRhcGQc.
Ejemplo\(\PageIndex{2}\)
Dos discos de hockey chocan oblicuamente mientras se deslizan sobre una superficie lisa, como se muestra a continuación. Supongamos que el coeficiente de restitución es 0.7 y el tiempo de impacto es 0.001s.
- ¿Cuál es la velocidad final de cada disco?
- ¿Cuál es la fuerza promedio ejercida sobre cada disco durante el impacto?
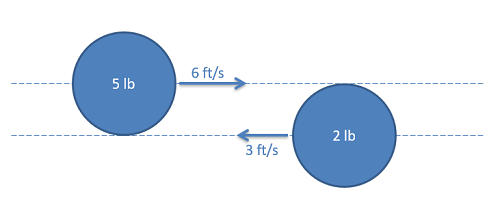
- Solución
-
Video\(\PageIndex{3}\): Solución trabajada a problema de ejemplo\(\PageIndex{2}\), proporcionado por el Dr. Majid Chatsaz. Fuente de YouTube: https://youtu.be/mRPjLk8RxQw.