1.3: Seguimiento de Posición Local - Odometría

El cálculo por cuentas, que rastrea la ubicación integrando la velocidad de un sistema de movimiento y rumbo a lo largo del tiempo, forma la columna vertebral de muchos sistemas de navegación de robots móviles. La forma más simple de muertos

Figura 1.1: Un robot móvil con pose\((x, y, \theta)\).

(a) El sensor de distancia Sharp IR

b) Curva de calibración

Figura 1.2: Sensor de distancia infrarrojo Sharp GP2Y0A21YK0F y su curva de calibración.

el cálculo de cuentas para vehículos terrestres es la odometría, que deriva la velocidad y la información de rumbo de las rotaciones de las ruedas percibidos.

Figura 1.3: Un codificador rotativo en cuadratura y su salida para rotación en sentido horario y antihorario.

\(d_{\text {wheel }}\)	\(2.71\)	pulgadas
\(L_{\text {baseline }}\)	\(5.25\)	pulgadas
\(N\)	\(60\)	garrapatas

Cuadro 1.1: Parámetros del robot móvil.

Al “resumir” los incrementos, podemos calcular las distancias acumuladas totales\(s_{\text {left }}\) y\(s_{\text {right }}\) recorridas por las ruedas izquierda y derecha, respectivamente.

Las variables time, LeftTticks y RightTicks de la asignación1. mat contienen tiempos de muestreo\(t^{k}\) (en segundos) y recuentos acumulativos de codificador izquierdo\(n_{\text {left }}\) y derecho y\(n_{\text {right }}\), respectivamente, registrados durante una sola ejecución de prueba de un robot móvil. Tenga en cuenta que la decodificación en cuadratura para rotación directa e inversa ya se ha incorporado en los datos, de tal manera que los recuentos acumulativos aumentan para la rotación hacia adelante y disminuyen para la rotación inversa. Los valores de las constantes de odometría para el robot móvil se dan en la Tabla\(1 .\)

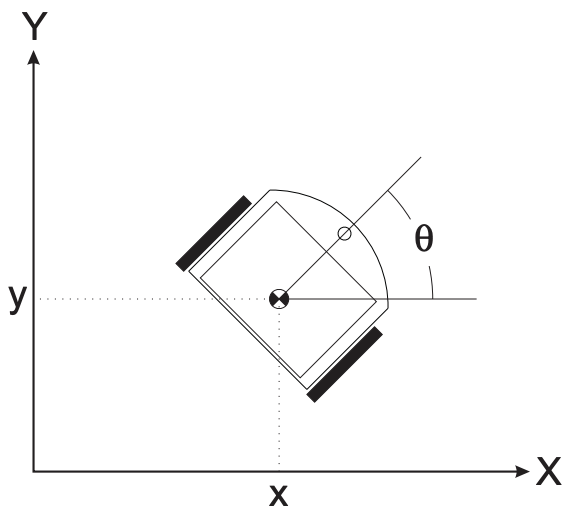
Para un robot móvil con tracción diferencial de dos ruedas, en el que las dos ruedas impulsadas (izquierda y derecha) puedan controlarse independientemente, las velocidades lineales\(v_{\text {left }}\) y\(v_{\text {right }}\) en las dos ruedas deben (suponiendo que no haya deslizamiento de las ruedas) estar ambas dirigidas hacia (u opuestas a) la dirección\(\theta\) del rumbo actual del robot. Así, el movimiento del robot puede describirse completamente por la velocidad\(v_{\text {center }}\) de un punto que se encuentra a medio camino entre las dos ruedas y la velocidad angular\(\omega\) alrededor de un centro de curvatura instantáneo (ICC) que se encuentra en algún lugar en línea con las dos ruedas, como se muestra en la Figura 1.4.

Figura 1.4: Trayectoria del robot.

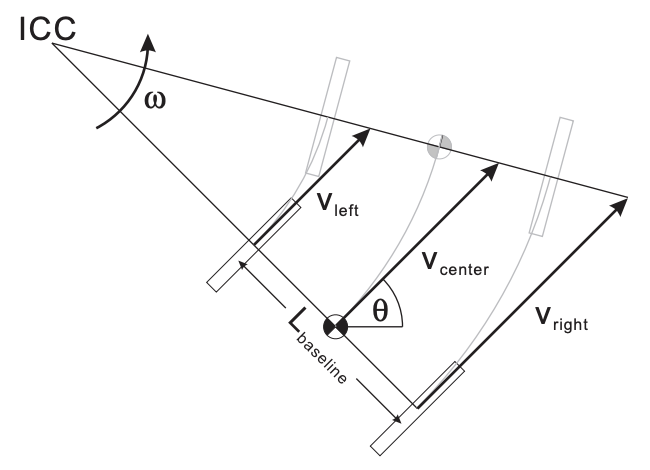
y\(L_{\rm baseline}\) es la distancia entre los puntos de contacto de las dos ruedas. Luego podemos integrar estas velocidades para rastrear la pose\([x(t), y(t), \theta(t)]\) del robot a lo largo del tiempo ya que\[\begin{aligned} &x(t)=\int_{0}^{t} v_{\text {center }}(t) \cos [\theta(t)] d t, \\ &y(t)=\int_{0}^{t} v_{\text {center }}(t) \sin [\theta(t)] d t, \\ &\theta(t)=\int_{0}^{t} \omega(t) d t . \end{aligned}\] en términos de los tiempos de muestreo\(t^{k}\), podemos escribir estas ecuaciones como\[\begin{aligned} x^{k} &=x^{k-1}+\int_{t^{k-1}}^{t^{k}} v_{\text {center }}(t) \cos [\theta(t)] d t, \\ y^{k} &=y^{k-1}+\int_{t^{k-1}}^{t^{k}} v_{\text {center }}(t) \sin [\theta(t)] d t, \\ \theta^{k} &=\theta^{k-1}+\int_{t^{k-1}}^{t^{k}} \omega(t) d t . \end{aligned}\]