9.2: Variables Aleatorias BiVariadas Discretas (Vectores Aleatorios)

Distribuciones Conjuntas

Hasta el momento, hemos considerado variables aleatorias escalares, cada una de cuyos resultados se describe por un solo valor. En esta sección, extendemos el concepto a variables aleatorias cuyo resultado son vectores. Por simplicidad, consideramos un vector aleatorio de la forma\[(X, Y) \text {, }\] donde\(X\) y\(Y\) toma\(J_{X}\) y\(J_{Y}\) valores, respectivamente. Así, el vector aleatorio\((X, Y)\) toma\(J=J_{X} \cdot J_{Y}\) valores. La función de masa de probabilidad asociada con\((X, Y)\) se denota por\(f_{X, Y}\). Similar al caso escalar, la función de masa de probabilidad asigna una probabilidad a cada uno de los posibles resultados, es decir,\[f_{X, Y}\left(x_{i}, y_{j}\right)=p_{i j}, \quad i=1, \ldots, J_{X}, \quad j=1, \ldots, J_{Y} .\] Una vez más, la función debe satisfacer\[\begin{aligned} 0 \leq p_{i j} \leq 1, \quad i=1, \ldots, J_{X}, \quad j=1, \ldots, J_{Y}, \\ \sum_{j=1}^{J_{Y}} \sum_{i=1}^{J_{X}} p_{i j} &=1 . \end{aligned}\] Antes de introducir conceptos clave que no existían para una variable aleatoria escalar, demos un ejemplo simple de probabilidad conjunta distribución.

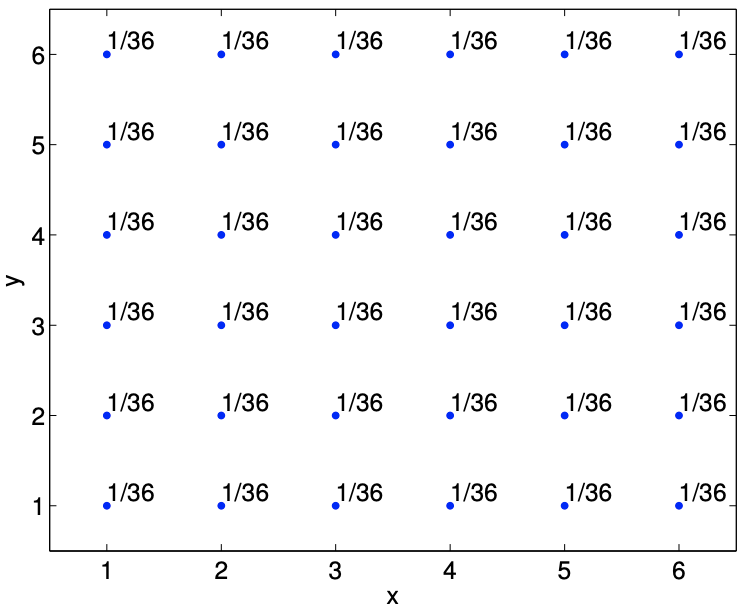
Ejemplo 9.2.1 rodando dos dados

Como primer ejemplo, consideremos rodar dos dados. El primer dado toma\(x_{i}=i, i=1, \ldots, 6\), y el segundo dado toma\(y_{j}=j, j=1, \ldots, 6\). El vector aleatorio asociado con rodar los dos dados es\[(X, Y),\] donde\(X\) toma\(J_{X}=6\) valores y\(Y\) toma\(J_{Y}=6\) valores. Así, el vector aleatorio\((X, Y)\) toma\(J=J_{X} \cdot J_{Y}=36\) valores. Porque (para un dado justo) cada uno de los 36 resultados es igualmente probable, la función de masa de probabilidad\(f_{X, Y}\) es\[f_{X, Y}\left(x_{i}, y_{j}\right)=\frac{1}{36}, \quad i=1, \ldots, 6, \quad j=1, \ldots, 6 .\] La función de masa de probabilidad se muestra gráficamente en la Figura\(\underline{9.4}\).

Figura 9.4: La función de masa de probabilidad para rodar dos dados.

Caracterización de distribuciones conjuntas

Ahora introduzcamos algunos conceptos adicionales útiles para describir distribuciones conjuntas. A lo largo de esta sección, consideramos un vector aleatorio\((X, Y)\) con la distribución de probabilidad asociada\(f_{X, Y}\). Primero está la densidad marginal, que se define como\[f_{X}\left(x_{i}\right)=\sum_{j=1}^{J_{Y}} f_{X, Y}\left(x_{i}, y_{j}\right), \quad i=1, \ldots, J_{X}\] En palabras, la densidad marginal de\(X\) es la distribución de probabilidad de\(X\) desatender\(Y\). Es decir, ignoramos el resultado de\(Y\), y nos hacemos la pregunta: ¿\(X\)Con qué frecuencia adquiere el valor\(x_{i}\)? Claramente, esto es igual a sumar la probabilidad conjunta\(f_{X, Y}\left(x_{i}, j_{j}\right)\) para todos los valores de\(y_{j}\). De igual manera, la densidad marginal para\(Y\) es De\[f_{Y}\left(y_{j}\right)=\sum_{i=1}^{J_{X}} f_{X, Y}\left(x_{i}, y_{j}\right), \quad j=1, \ldots, J_{Y}\] nuevo, en este caso, ignoramos el resultado de\(X\) y preguntamos: ¿\(Y\)Con qué frecuencia adquiere el valor\(y_{j}\)? Obsérvese que las densidades marginales son distribuciones de probabilidad válidas porque\[f_{X}\left(x_{i}\right)=\sum_{j=1}^{J_{Y}} f_{X, Y}\left(x_{i}, y_{j}\right) \leq \sum_{k=1}^{J_{X}} \sum_{j=1}^{J_{Y}} f_{X, Y}\left(x_{k}, y_{j}\right)=1, \quad i=1, \ldots, J_{X}\] y\[\sum_{i=1}^{J_{X}} f_{X}\left(x_{i}\right)=\sum_{i=1}^{J_{X}} \sum_{j=1}^{J_{Y}} f_{X, Y}\left(x_{i}, y_{j}\right)=1\] El segundo concepto es la probabilidad condicional, que es la probabilidad que\(X\) toma el valor\(x_{i}\) dado\(Y\) ha tomado el valor \(y_{j}\). La probabilidad condicional se denota por\[f_{X \mid Y}\left(x_{i} \mid y_{j}\right), \quad i=1, \ldots, J_{X}, \quad \text { for a given } y_{j}\] La probabilidad condicional se puede expresar como\[f_{X \mid Y}\left(x_{i} \mid y_{j}\right)=\frac{f_{X, Y}\left(x_{i}, y_{j}\right)}{f_{Y}\left(y_{j}\right)} .\] En palabras, la probabilidad que\(X\) adquiere\(x_{i}\) dado que\(Y\) ha asumido\(y_{j}\) es igual a la probabilidad que ambos eventos asumen\(\left(x_{i}, y_{j}\right)\) normalizados por la probabilidad que\(Y\) toma\(y_{j}\) despreciar\(x_{i}\). Podemos considerar una interpretación diferente de la relación reordenando la ecuación como\[f_{X, Y}\left(x_{i}, y_{j}\right)=f_{X \mid Y}\left(x_{i} \mid y_{j}\right) f_{Y}\left(y_{j}\right)\] y luego sumando\(j\) para ceder\[f_{X}\left(x_{i}\right)=\sum_{j=1}^{J_{Y}} f\left(x_{i}, y_{j}\right)=\sum_{j=1}^{J_{Y}} f_{X \mid Y}\left(x_{i} \mid y_{j}\right) f_{Y}\left(y_{j}\right) .\] En otras palabras, la probabilidad marginal de\(X\) asumir\(x_{i}\) es igual a la suma de la probabilidades de\(X\) asumir\(x_{i}\) dado\(Y\) ha asumido\(y_{j}\) multiplicado por la probabilidad de\(Y\) asumir\(y_{j}\) despreciar\(x_{i}\).

De (9.2), podemos derivar la ley de Bayes (o teorema de Bayes), una regla útil que relaciona probabilidades condicionales de dos eventos. Primero, intercambiamos los roles de\(x\) y\(y\) en\(\underline{(9.2)}\), obteniendo\[f_{Y, X}\left(y_{j}, x_{i}\right)=f_{Y \mid X}\left(y_{j} \mid x_{i}\right) f_{X}\left(x_{i}\right) .\] Pero, ya que\(f_{Y, X}\left(y_{j}, x_{i}\right)=f_{X, Y}\left(x_{i}, y_{j}\right)\),\[f_{Y \mid X}\left(y_{j} \mid x_{i}\right) f_{X}\left(x_{i}\right)=f_{X \mid Y}\left(x_{i} \mid y_{j}\right) f_{Y}\left(y_{j}\right),\] y reordenando la ecuación arroja La\[f_{Y \mid X}\left(y_{j} \mid x_{i}\right)=\frac{f_{X \mid Y}\left(x_{i} \mid y_{j}\right) f_{Y}\left(y_{j}\right)}{f_{X}\left(x_{i}\right)} .\] ecuación (9.3) se llama ley de Bayes. La regla tiene muchas aplicaciones útiles en las que podríamos conocer una densidad condicional y deseamos inferir la otra densidad condicional. (También observamos que el teorema es fundamental para la estadística bayesiana y, por ejemplo, se explota en la estimación y los problemas inversos, problemas de inferir los parámetros subyacentes de un sistema a partir de mediciones.)

Ejemplo 9.2.2 Densidad marginal y condicional de rodar dos dados

Repasemos el ejemplo de rodar dos dados e ilustremos cómo se computan la densidad marginal y la densidad condicional. Recordamos que la función de masa de probabilidad para el problema es\[f_{X, Y}(x, y)=\frac{1}{36}, \quad x=1, \ldots, 6, y=1, \ldots, 6 .\] El cálculo de la densidad marginal de\(X\) se ilustra en la Figura 9.5 (a). Para cada uno\(x_{i}\)\(i=1, \ldots, 6\),, tenemos También\[f_{X}\left(x_{i}\right)=\sum_{j=1}^{6} f_{X, Y}\left(x_{i}, y_{j}\right)=\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}+\frac{1}{36}=\frac{1}{6}, \quad i=1, \ldots, 6 .\] podemos deducir esto de la intuición y llegar a la misma conclusión. Recordemos que la densidad marginal de\(X\) es la densidad de probabilidad de\(X\) ignorar el resultado de\(Y\). Para este rodado de dos dados

a) densidad marginal,\(f_{X}\)

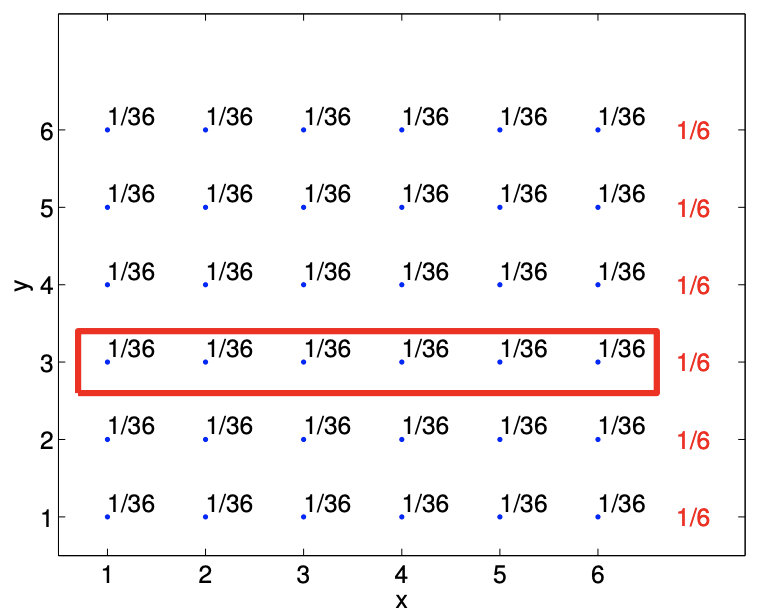
b) densidad marginal,\(f_{Y}\)

Figura 9.5: Ilustración del cálculo de densidad marginal\(f_{X}(x=2)\) y\(f_{Y}(y=3)\).

ejemplo, simplemente corresponde a la distribución de probabilidad de laminación de una sola matriz, que es claramente igual a Cálculo\[f_{X}(x)=\frac{1}{6}, \quad x=1, \ldots, 6 .\] similar de la densidad marginal de\(Y, f_{Y}\), se ilustra en la Figura\(9.5(\mathrm{~b})\). En este caso, ignorando el primer dado\((X)\), el segundo dado produce\(y_{j}=j, j=1, \ldots, 6\), con la misma probabilidad de\(1 / 6\).

Ilustremos ahora el cálculo de la probabilidad condicional. Como primer ejemplo, calculemos la probabilidad condicional de\(X\) dado\(Y\). En particular, digamos que se nos da\(y=3\). Como se muestra en la Figura 9.6 (a), la probabilidad conjunta de todos los resultados excepto los correspondientes\(y=3\) son irrelevantes (región sombreada). Dentro de la región con\(y=3\), tenemos seis posibles resultados, cada uno con la misma probabilidad. Así, tenemos\[f_{X \mid Y}(x \mid y=3)=\frac{1}{6}, \quad x=1, \ldots, 6\] Note que, podemos computar esto simplemente considerando el conjunto selecto de probabilidades conjuntas\(f_{X, Y}(x, y=\) 3) y re-normalizando las probabilidades por su suma. En otras palabras,\[f_{X \mid Y}(x \mid y=3)=\frac{f_{X, Y}(x, y=3)}{\sum_{i=1}^{6} f_{X, Y}\left(x_{i}, y=3\right)}=\frac{f_{X, Y}(x, y=3)}{f_{Y}(y=3)}\] que es precisamente igual a la fórmula que hemos introducido anteriormente.

De igual manera, la Figura\(9.6(\mathrm{~b})\) ilustra el cálculo de la probabilidad condicional\(f_{Y \mid X}(y, x=2)\). En este caso, solo consideramos la distribución conjunta de probabilidad de\(f_{X, Y}(x=2, y)\) y re-normalizar la densidad por\(f_{X}(x=2)\).

a) densidad condicional,\(f_{X \mid Y}(x \mid y=3)\)

b) densidad condicional,\(f_{Y \mid X}(y \mid x=2)\)

Figura 9.6: Ilustración del cálculo de densidad condicional\(f_{X \mid Y}(x \mid y=3)\) y\(f_{Y \mid X}(y \mid x=2)\).

El hecho de que la densidad de probabilidad sea simplemente un producto de densidades marginales significa que podemos dibujar\(X\) y\(Y\) separadamente según su respectiva probabilidad marginal y luego formar el vector aleatorio\((X, Y)\).

Usando la probabilidad condicional, podemos conectar nuestra comprensión intuitiva de la independencia con la definición precisa. A saber, es\[f_{X \mid Y}\left(x_{i} \mid y_{j}\right)=\frac{f_{X, Y}\left(x_{i}, y_{j}\right)}{f_{Y}\left(y_{j}\right)}=\frac{f_{X}\left(x_{i}\right) f_{Y}\left(y_{j}\right)}{f_{Y}\left(y_{j}\right)}=f_{X}\left(x_{i}\right)\] decir, la probabilidad condicional de\(X\) dar no\(Y\) es diferente de la probabilidad que\(X\) adquiere\(x\) despreciar\(y\). En otras palabras, conocer el resultado de no\(Y\) agrega información adicional sobre el resultado de\(X\). Esto concuerda con nuestro sentido intuitivo de independencia.

Hemos discutido la noción de “o” y la relacionamos con la unión de dos conjuntos. Discutamos ahora brevemente la noción de “y” en el contexto de la probabilidad conjunta. Primero, tenga en cuenta que\(f_{X, Y}(x, y)\) es la probabilidad de que\(X=x\) y\(Y=y\), es decir,\(f_{X, Y}(x, y)=P(X=x\) y\(Y=y)\). De manera más general, considerar dos eventos\(A\) y\(B\), y en particular\(A\) y\(B\), que es la intersección de\(A\) y\(B\),\(A \cap B\). Si los dos eventos son independientes, entonces\[P(A \text { and } B)=P(A) P(B)\] y por lo tanto\(f_{X, Y}(x, y)=f_{X}(x) f_{Y}(y)\) que podemos pensar como probabilidad de\(P(A \cap B)\). Pictorialmente, podemos asociar el evento\(A\) con la\(X\) toma de un valor especificado como se marca en la Figura\(9.5(\) a\()\) y el evento\(B\) con la\(Y\) toma de un valor especificado como se marca en la Figura 9.5 ( b). La intersección de\(A\) y\(B\) es la intersección de las dos regiones marcadas, y la probabilidad conjunta\(f_{X, Y}\) es la probabilidad asociada a esta intersección.

Para solidificar la idea de independencia, consideremos dos ejemplos canónicos que involucran volteretas de monedas.

Ejemplo 9.2.3 Eventos independientes: dos variables aleatorias asociadas con dos volteretas de monedas independientes

Consideremos voltear dos monedas justas. Asociamos el resultado de voltear la primera y segunda monedas con variables aleatorias\(X\) y\(Y\), respectivamente. Además, asociamos los valores de 1 y

Figura 9.7: La función de masa de probabilidad para voltear dos monedas independientes.

0 a cabeza y cola, respectivamente. Podemos asociar las dos volteretas con un vector aleatorio\((X, Y)\), cuyos posibles resultados son\[(0,0), \quad(0,1), \quad(1,0), \quad \text { and }(1,1)\] intuitivamente, las dos variables\(X\) y\(Y\) serán independientes si el resultado del segundo flip, descrito por\(Y\), no está influenciado por el resultado del primer volteo, descrito por\(X\), y viceversa.

Postulamos que es igualmente probable obtener cualquiera de los cuatro resultados, de tal manera que la función conjunta de masa de probabilidad viene dada por\[f_{X, Y}(x, y)=\frac{1}{4}, \quad(x, y) \in\{(0,0),(0,1),(1,0),(1,1)\}\] Mostramos ahora que esta suposición implica independencia, como esperaríamos intuitivamente. En particular, la densidad de probabilidad marginal de\(X\) es\[f_{X}(x)=\frac{1}{2}, \quad x \in\{0,1\}\] desde\((\) decir\() P(X=0)=P((X, Y)=(0,0))+P((X, Y)=(0,1))=1 / 2\). De igual manera, la densidad marginal de probabilidad de\(Y\) es Ahora\[f_{Y}(y)=\frac{1}{2}, \quad y \in\{0,1\}\] notamos\[f_{X, Y}(x, y)=f_{X}(x) \cdot f_{Y}(y)=\frac{1}{4}, \quad(x, y) \in\{(0,0),(0,1),(1,0),(1,1)\}\] lo que es la definición de independencia.

La función de masa de probabilidad\((X, Y)\) y la densidad marginal de\(X\) y se\(Y\) muestran en la Figura 9.7. La figura muestra claramente que la densidad articular de\((X, Y)\) es el producto de la densidad marginal de\(X\) y\(Y\). Demostremos que esto concuerda con nuestra intuición, en particular al considerar la probabilidad de\((X, Y)=(0,0)\). Primero, la frecuencia relativa que\(X\) toma 0 es\(1 / 2\). Segundo, de los hechos en cuál\(X=0,1 / 2\) de estos asumen\(Y=0\). Tenga en cuenta que esta probabilidad es independiente del valor que\(X\) tome. Así, la frecuencia relativa de\(X\) tomar 0 y\(Y\) tomar 0 es\(1 / 2\) de\(1 / 2\), que es igual a\(1 / 4\).

Figura 9.8: La función de masa de probabilidad para voltear dos monedas independientes.

También podemos considerar la probabilidad condicional de un evento que\(X\) toma 1 dado que\(Y\) toma 0. La probabilidad condicional es\[f_{X \mid Y}(x=1 \mid y=0)=\frac{f_{X, Y}(x=1, y=0)}{f_{Y}(y=0)}=\frac{1 / 4}{1 / 2}=\frac{1}{2} .\] Esta probabilidad es igual a la probabilidad marginal de\(f_{X}(x=1)\). Esto concuerda con nuestra intuición; dado que dos eventos son independientes, no obtenemos información adicional sobre el resultado\(X\) de conocer el resultado de\(Y\).

Ejemplo 9.2.4 eventos no independientes: dos variables aleatorias asociadas a una sola

Consideremos ahora voltear una sola moneda. Asociamos una variable aleatoria de Bernoulli\(X\) y\(Y\) con\[X=\left\{\begin{array}{ll} 1, & \text { head } \\ 0, & \text { tail } \end{array} \quad \text { and } Y=\left\{\begin{array}{ll} 1, & \text { tail } \\ 0, & \text { head } \end{array} .\right.\right.\] Note que da como resultado una cabeza\((X, Y)=(1,0)\), mientras que una cola resulta en\((X, Y)=(0,1)\). Intuitivamente, las variables aleatorias no son independientes, porque el resultado de determina\(X\) completamente\(Y\), i.e\(X+Y=1\).

Demostremos que estas dos variables no son independientes. Estamos igualmente como conseguir una cabeza,\((1,0)\), o una cola,\((0,1)\). No podemos producir\((0,0)\), porque la moneda no puede ser cabeza y cola al mismo tiempo. De igual manera,\((1,1)\) tiene probablemente de cero. Así, la función de densidad de probabilidad conjunta es\[f_{X, Y}(x, y)= \begin{cases}\frac{1}{2}, & (x, y)=(0,1) \\ \frac{1}{2}, & (x, y)=(1,0) \\ 0, & (x, y)=(0,0) \text { or }(x, y)=(1,1) .\end{cases}\] La función de masa de probabilidad se ilustra en la Figura\(\underline{9.8}\).

La densidad marginal de cada uno de los eventos es la misma que antes,\(X\) es decir, es igualmente probable que tome 0 o 1, y\(Y\) es igualmente similar a tomar 0 o 1. Así, tenemos\[\begin{aligned} &f_{X}(x)=\frac{1}{2}, \quad x \in\{0,1\} \\ &f_{Y}(y)=\frac{1}{2}, \quad y \in\{0,1\} . \end{aligned}\] For\((x, y)=(0,0)\), tenemos a\[f_{X, Y}(x, y)=0 \neq \frac{1}{4}=f_{X}(x) \cdot f_{Y}(y) .\] So,\(X\) y no\(Y\) somos independientes.

También podemos considerar probabilidades condicionales. La probabilidad condicional de\(x=1\) dado que\(y=0\) es\[f_{X \mid Y}(x=1 \mid y=0)=\frac{f_{X, Y}(x=1, y=0)}{f_{Y}(y=0)}=\frac{1 / 2}{1 / 2}=1 .\] En palabras, dado que sabemos\(Y\) toma 0, sabemos que\(X\) toma 1. Por otro lado, la probabilidad condicional de\(x=1\) dado que\(y=1\) es\[f_{X \mid Y}(x=0 \mid y=0)=\frac{f_{X, Y}(x=0, y=0)}{f_{Y}(y=0)}=\frac{0}{1 / 2}=0 .\] En palabras, dado que\(Y\) toma en 1, no hay manera que\(X\) tome en 1. A diferencia del ejemplo anterior que\((X, Y)\) asociaba a dos volteretas de monedas independientes, conocemos con certeza el resultado de\(X\) dado el resultado de\(Y\), y viceversa.

Hemos visto que la independencia es una forma de describir la relación entre dos eventos. La independencia es una idea binaria; o dos eventos son independientes o no independientes. Otro concepto que describe lo estrechamente que se relacionan dos eventos es la correlación, que es una covarianza normalizada. La covarianza de dos variables aleatorias\(X\) y\(Y\) se denota por\(\operatorname{Cov}(X, Y)\) y se define como\[\operatorname{Cov}(X, Y) \equiv E\left[\left(X-\mu_{X}\right)\left(Y-\mu_{Y}\right)\right] .\] La correlación de\(X\) y\(Y\) se denota por\(\rho_{X Y}\) y se define como\[\rho_{X Y}=\frac{\operatorname{Cov}(X, Y)}{\sigma_{X} \sigma_{Y}},\] donde recordar que\(\sigma_{X}\) y\(\sigma_{Y}\) son la desviación estándar de\(X\) y\(Y\), respectivamente. La correlación indica cuán fuertemente se relacionan dos eventos aleatorios y toma un valor entre\(-1\) y 1. En particular, dos eventos perfectamente correlacionados toman 1 (o\(-1\)), y dos eventos independientes toman 0.

Dos eventos independientes tienen correlación cero porque\[\begin{aligned} \operatorname{Cov}(X, Y) &=E\left[\left(X-\mu_{X}\right)\left(Y-\mu_{Y}\right)\right]=\sum_{j=1}^{J_{Y}} \sum_{i=1}^{J_{X}}\left(x_{i}-\mu_{X}\right)\left(y_{j}-\mu_{Y}\right) f_{X, Y}\left(x_{i}, y_{j}\right) \\ &=\sum_{j=1}^{J_{Y}} \sum_{i=1}^{J_{X}}\left(x_{i}-\mu_{X}\right)\left(y_{j}-\mu_{Y}\right) f_{X}\left(x_{i}\right) f_{Y}\left(y_{j}\right) \\ &=\left[\sum_{j=1}^{J_{Y}}\left(y_{j}-\mu_{Y}\right) f_{Y}\left(y_{j}\right)\right] \cdot\left[\sum_{i=1}^{J_{X}}\left(x_{i}-\mu_{X}\right) f_{X}\left(x_{i}\right)\right] \\ &=E\left[Y-\mu_{Y}\right] \cdot E\left[X-\mu_{X}\right]=0 \cdot 0=0 . \end{aligned}\] La tercera desigualdad se deriva de la definición de independencia,\(f_{X, Y}\left(x_{i}, y_{j}\right)=f_{X}\left(x_{i}\right) f_{Y}\left(y_{j}\right)\). Así, si las variables aleatorias son independientes, entonces no están correlacionadas. Sin embargo, lo contrario no es cierto en general.